三角形的外角
图片预览






文档简介
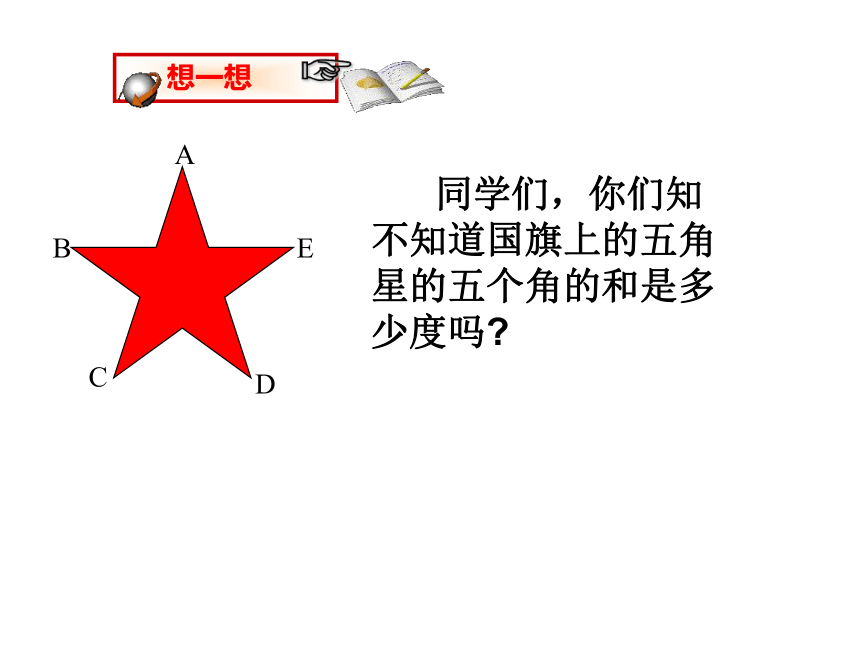
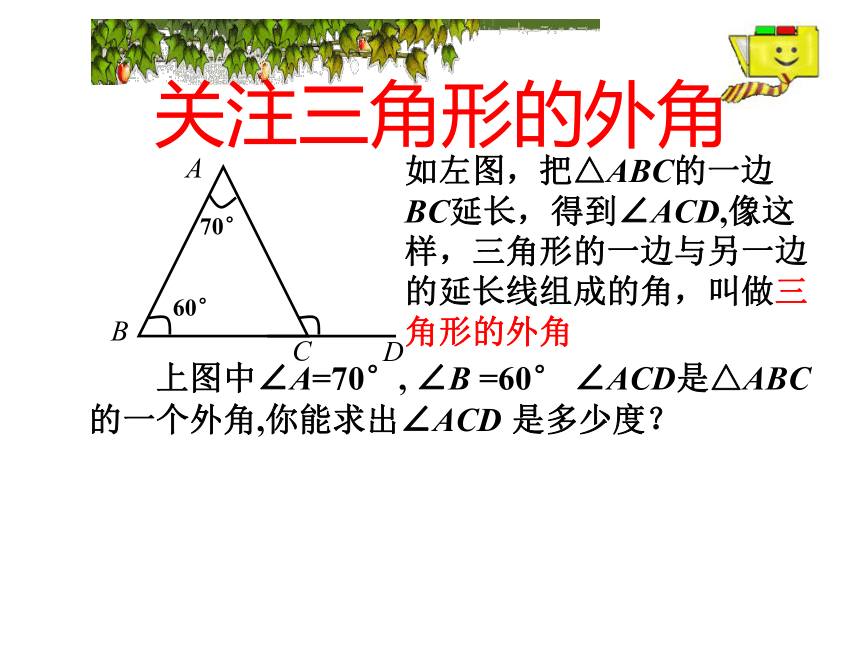
课件30张PPT。三角形的内角是三角形内部的骄子什么都没有呀,让人感到很无奈那三角形的外部呢?只要你添上一笔就精彩了α外角6.6 关注三角形的外角 那就让我们 同学们,你们知不知道国旗上的五角星的五个角的和是多少度吗?关注三角形的外角如左图,把△ABC的一边BC延长,得到∠ACD,像这样,三角形的一边与另一边的延长线组成的角,叫做三角形的外角 上图中∠A=70°, ∠B =60° ∠ACD是△ABC的一个外角,你能求出∠ACD 是多少度?画图并思考: 画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?归纳: 每一个三角形都有6个外角.
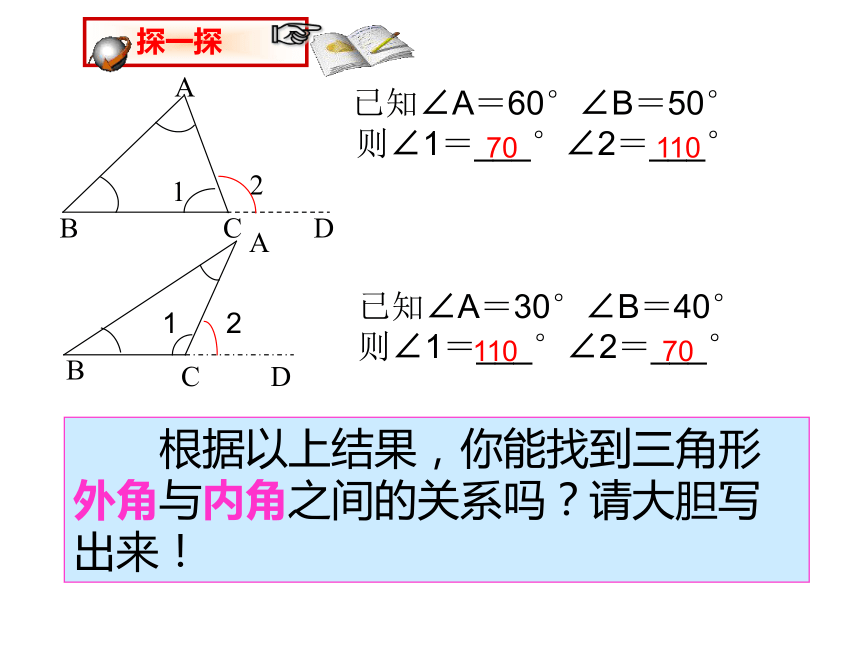
每一个顶点相对应的外角都有2个.每个外角与相应的内角是邻补角. 已知∠A=60°∠B=50°则∠1=___°∠2=___°已知∠A=30°∠B=40°则∠1=___°∠2=___° 根据以上结果,你能找到三角形外角与内角之间的关系吗?请大胆写出来!7011011070关注三角形的外角由上边的计算结果,你发现了什么你能得到什么结论三角形的一个外角等于和它不相邻的两个内角的和.
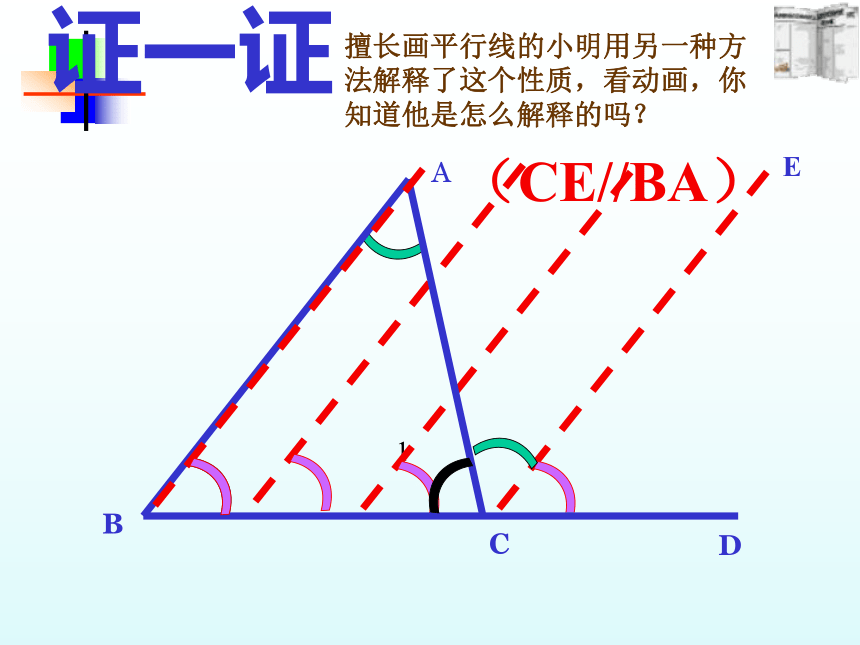
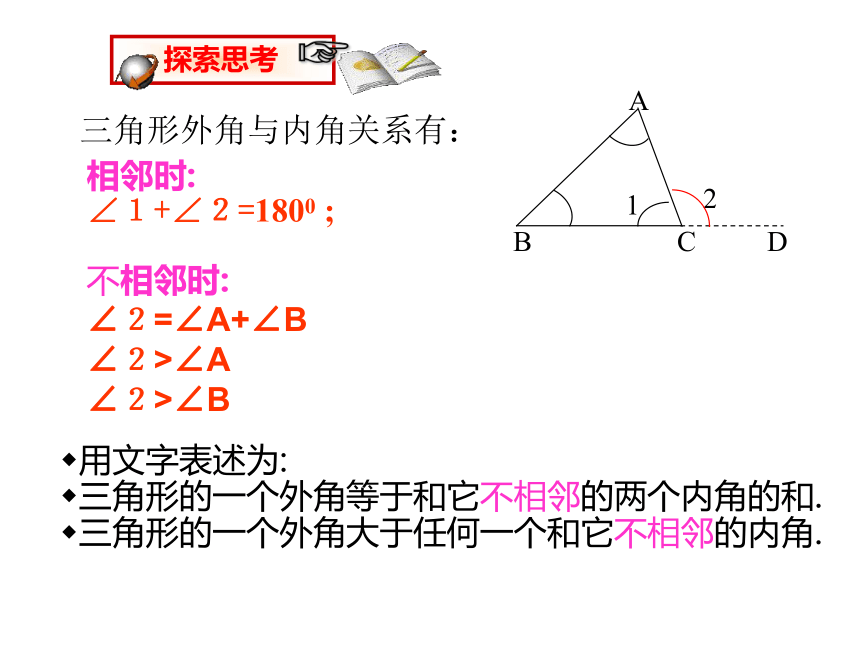
三角形的一个外角大于任何一个和它不相邻的内角.1(CE//BA)AE证一证擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?CBD三角形外角与内角关系有:相邻时:
∠1+∠2=1800 ;
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.不相邻时:
∠2=∠A+∠B
∠2>∠A
∠2>∠B
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用. 三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.数学语言推论1: ∠2=∠A+∠B.
推论2: ∠2>∠A;
∠2>∠B;
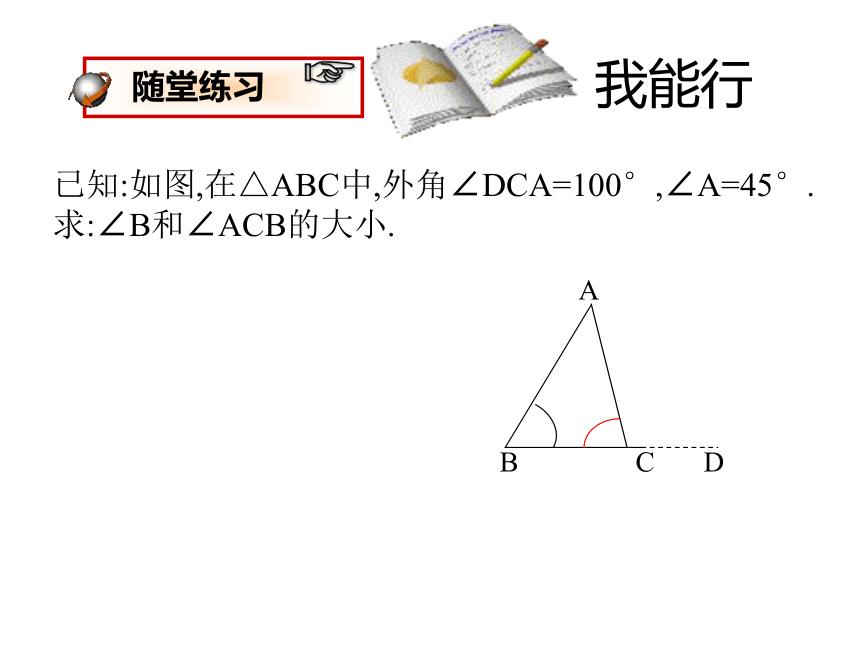
3、三角形的一个外角大于任何一个与它不相邻的内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:我能行已知:如图,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小. 如图,D 是△ABC 的BC 边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B 的度数;
(2)∠C 的度数.典型例题5.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.AEGFCB探究如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?三角形的外角和定理:
三角形的外角和等于360°
议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∠3= ∠4BC123A∠2= ∠BAD所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°“行家”看“门道” 已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和), ∴ AD ∥BC(内错角相等,两直线平行). ∠B=∠C (已知), ∴∠DAC=∠C(等量代换).分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”. ∵ AD平分 ∠EAC(已知).∴∠C= ∠EAC(等式性质).∴∠DAC= ∠EAC(角平分线的定义).··例题是运用了定理“内错角相等,两直线平行”得到了证实.已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.证明(1):∵ ∠BDC是△DCE的一个外角 (外角意义), ∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).∴ ∠BDC>∠A (不等式的性质).∵ ∠DEC是△ABE的一个外角 (外角意义),关注三角形的外角已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义), ∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).∴ ∠BDC=∠A+∠B+∠C (等式的性质).∵ ∠DEC是△ABE的一个外角 (外角意义),关注三角形的外角已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.解:∵∠1是△BDF的一个外角
∴ ∠1=∠B+∠D分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.又∵∠A+∠1+∠2=180°( ? )又 ∵ ∠2是△EHC的一个外角
∴ ∠2=∠C+∠E
∴ ∠A+∠B+∠C+∠D+∠E =180°想一想练一练∠A+∠B+∠C+∠D+∠E+∠F= .ADECFB360°NPM判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )例题2:在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80° ∠C=30 °
(1)求∠DAE
(2)你能发现∠DAE与∠B、∠C的关系吗?
(3)若只知∠B-∠C=20°,你能求出∠DAE吗?△ABC中,∠B、∠C的内角(外角)平分线交于D,已知∠A=x°,用x的式子表示∠BDC
如图,类似于三角形,我们称
∠1+ ∠2+ ∠3+ ∠4为四边形的外角和,
已知四边形的内角和为360o,你能用今
天所学的方法进行推理计算吗?能知道
多边形的外角和吗?思考已知:P是△ABC内一点。
求证:∠BPC>∠BAC关注三角形的外角三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.△ABC中:
推论1: ∠2=∠A+∠B.
推论2: ∠2>∠A;
∠2>∠B;
这个结论以后可以直接运用.6.6 关注三角形的外角嘉善五中 江秀春 俞利忠
每一个顶点相对应的外角都有2个.每个外角与相应的内角是邻补角. 已知∠A=60°∠B=50°则∠1=___°∠2=___°已知∠A=30°∠B=40°则∠1=___°∠2=___° 根据以上结果,你能找到三角形外角与内角之间的关系吗?请大胆写出来!7011011070关注三角形的外角由上边的计算结果,你发现了什么你能得到什么结论三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.1(CE//BA)AE证一证擅长画平行线的小明用另一种方法解释了这个性质,看动画,你知道他是怎么解释的吗?CBD三角形外角与内角关系有:相邻时:
∠1+∠2=1800 ;
用文字表述为:
三角形的一个外角等于和它不相邻的两个内角的和.
三角形的一个外角大于任何一个和它不相邻的内角.不相邻时:
∠2=∠A+∠B
∠2>∠A
∠2>∠B
在这里,我们通过三角形内角和定理直接推导出两个新定理.像这样,由一个公理或定理直接推出的定理,叫做这个公理或定理的推论(corollary).
推论可以当作定理使用. 三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.数学语言推论1: ∠2=∠A+∠B.
推论2: ∠2>∠A;
∠2>∠B;
3、三角形的一个外角大于任何一个与它不相邻的内角。2、三角形的一个外角等于与它不相邻的两个内角的和;1、三角形的一个外角与它相邻的内角互补;三角形的外角与内角的关系:我能行已知:如图,在△ABC中,外角∠DCA=100°,∠A=45°.
求:∠B和∠ACB的大小. 如图,D 是△ABC 的BC 边上一点,
∠B=∠BAD,∠ADC=80°,
∠BAC=70°.
求:(1)∠B 的度数;
(2)∠C 的度数.典型例题5.如图:已知在△ABC中,EF与AC交于点G,与BC的延长线交于点F,∠B=450 ,∠F=300,∠CGF=700,
求∠A的度数.AEGFCB探究如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,你能利用三角形的内角和等于1800求出这三个外角的和吗?三角形的外角和定理:
三角形的外角和等于360°
议一议∠2+ ∠ABC=180°∠3+ ∠ACB=180°三个式子相加得到∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°而∠BAC+ ∠ABC+∠ACB=180°∠1+ ∠2+ ∠3=360°解:过A作AD平行于BC∠3= ∠4BC123A∠2= ∠BAD所以, ∠1+ ∠2+ ∠3= ∠1+ ∠4+ ∠BAD=360°“行家”看“门道” 已知:如右图,在△ABC中,AD平分外角∠EAC,∠B= ∠C. 求证:AD∥BC.证明:∵ ∠EAC=∠B+∠C (三角形的一个外角等于和它不相邻的两个内角的和), ∴ AD ∥BC(内错角相等,两直线平行). ∠B=∠C (已知), ∴∠DAC=∠C(等量代换).分析:要证明AD∥BC,只需要证明“同位角相等”,“内错角相等”或“同旁内角互补”. ∵ AD平分 ∠EAC(已知).∴∠C= ∠EAC(等式性质).∴∠DAC= ∠EAC(角平分线的定义).··例题是运用了定理“内错角相等,两直线平行”得到了证实.已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.证明(1):∵ ∠BDC是△DCE的一个外角 (外角意义), ∴ ∠BDC>∠CED(三角形的一个外角大于和它不相邻的任何一个外角).∴ ∠DEC>∠A(三角形的一个外角大于和它不相邻的任何一个外角).∴ ∠BDC>∠A (不等式的性质).∵ ∠DEC是△ABE的一个外角 (外角意义),关注三角形的外角已知:如图所示.
求证:(1)∠BDC>∠A;
(2) ∠BDC=∠A+∠B+∠C.证明(2):∵ ∠BDC是△DCE的一个外角 (外角意义), ∴ ∠BDC =∠C+∠CED(三角形的一个外角等于和它不相邻的两个内角的和).∴ ∠DEC=∠A+ ∠B(三角形的一个外角等于和它不相邻的两个外角的和).∴ ∠BDC=∠A+∠B+∠C (等式的性质).∵ ∠DEC是△ABE的一个外角 (外角意义),关注三角形的外角已知:五角星如图所示.
求:∠A+∠B+∠C+∠D+∠E的度数.解:∵∠1是△BDF的一个外角
∴ ∠1=∠B+∠D分析:设法利用外角把这五个角“凑”到一个三角形中,运用三角形内角和定理来求解.又∵∠A+∠1+∠2=180°( ? )又 ∵ ∠2是△EHC的一个外角
∴ ∠2=∠C+∠E
∴ ∠A+∠B+∠C+∠D+∠E =180°想一想练一练∠A+∠B+∠C+∠D+∠E+∠F= .ADECFB360°NPM判断题:1、三角形的外角和是指三角形所有外角的和。( )
2、三角形的外角和等于它内角和的2倍。( )
3、三角形的一个外角等于两个内角的和。( )
4、三角形的一个外角等于与它不相邻的两个内角的和。( )
5、三角形的一个外角大于任何一个内角。( )
6、三角形的一个内角小于任何一个与它不相邻的外角。( )例题2:在△ABC中,AD⊥BC,AE平分∠BAC,∠B=80° ∠C=30 °
(1)求∠DAE
(2)你能发现∠DAE与∠B、∠C的关系吗?
(3)若只知∠B-∠C=20°,你能求出∠DAE吗?△ABC中,∠B、∠C的内角(外角)平分线交于D,已知∠A=x°,用x的式子表示∠BDC
如图,类似于三角形,我们称
∠1+ ∠2+ ∠3+ ∠4为四边形的外角和,
已知四边形的内角和为360o,你能用今
天所学的方法进行推理计算吗?能知道
多边形的外角和吗?思考已知:P是△ABC内一点。
求证:∠BPC>∠BAC关注三角形的外角三角形内角和定理的推论:
推论1: 三角形的一个外角等于和它不相邻的两个内角的和.
推论2: 三角形的一个外角大于任何一个和它不相邻的内角.△ABC中:
推论1: ∠2=∠A+∠B.
推论2: ∠2>∠A;
∠2>∠B;
这个结论以后可以直接运用.6.6 关注三角形的外角嘉善五中 江秀春 俞利忠
