13.1.1轴对称
图片预览








文档简介
课件54张PPT。13.1.1轴对称要仔细观察哦!轴 对 称 如果____________ 沿一条直线折叠,直线两旁的部分能够_____________,这个图形就叫做______________.这条直线就是它的__________.
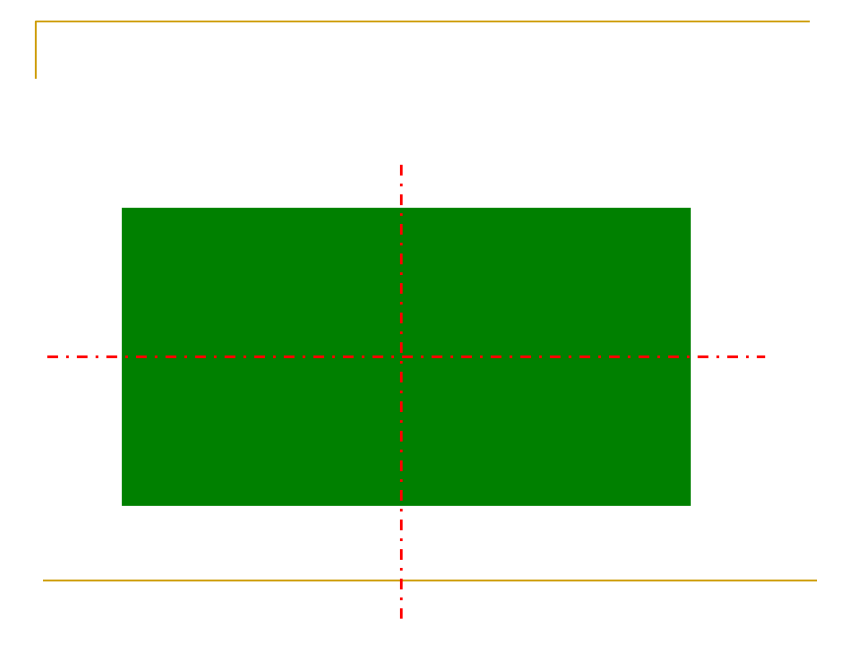
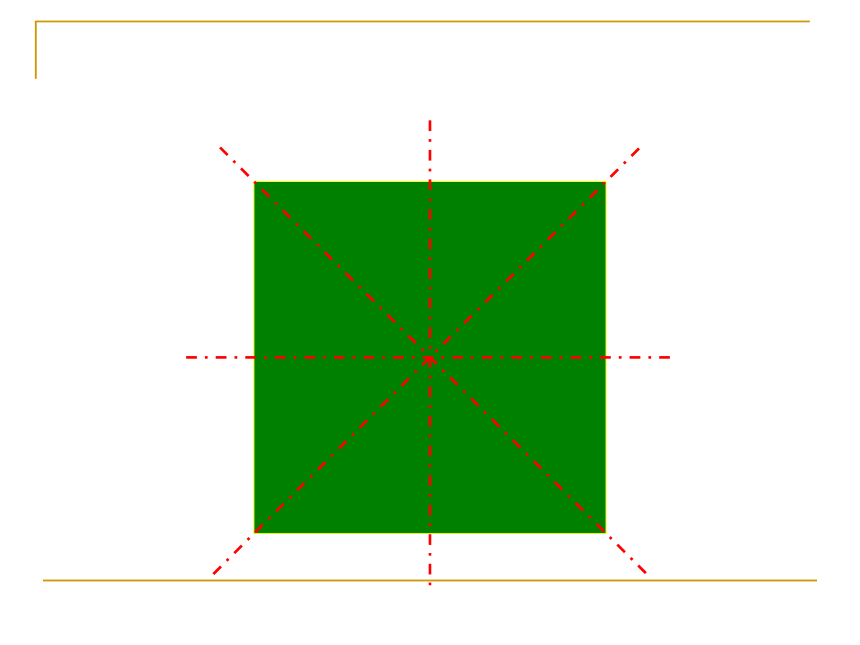
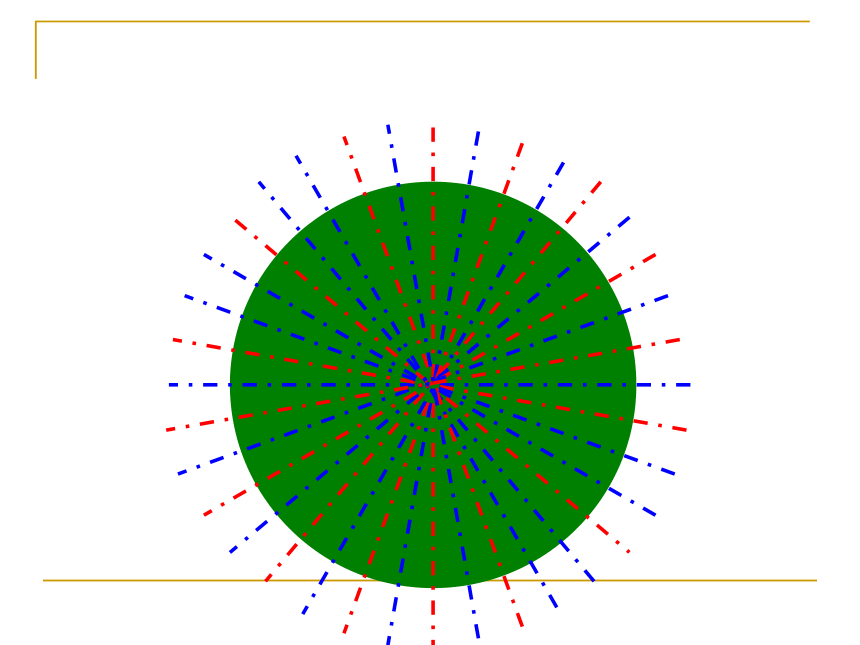
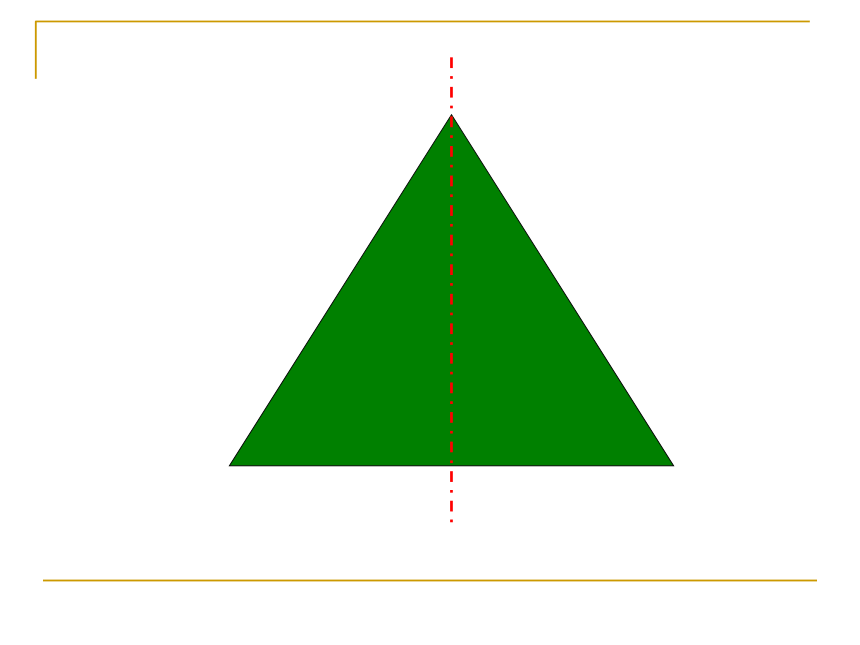
一个平面图形互相重合轴对称图形对称轴定 义课堂练习 练习1 如图所示的每个图形是轴对称图形吗?如
果是,指出它的对称轴. (1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。 (2)对称轴通常画成虚线,是直线,不能画成线段。对称轴问题下面两个图形有什么共同特点?1.把_______沿着某一条直线折叠,如果它能够与_____图形____,那么就说这两个图形______________或者说这两个图形成轴对称。
2.同样,我们把这条直线叫做______.
3.折叠后重合的点是对应点,叫做______.一个图形另一个重合关于这条直线对称对称轴对称点定义ABCA′B′C′对称点D D′对称轴做P60页第二题 下列给出的每幅图形中的两个图案是轴对称吗?如果是,试着找出它们的对称轴。喜喜FF(A)(C)(B)练习:不是轴对称图形两个图形成轴对称想一想想一想:1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3.都有对称轴复习线段的垂线和线段的中点
线段垂直平分线的定义探索新知 问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系? 成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段. Ho 轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线. 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? NPo 不折叠图形,你能准确地作出轴对称图形的对称
轴吗? 作线段的垂直平分线 有时我们感觉两个平面图形是轴对称的,如何验
证呢?喜喜(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
那么利用尺规还能解决什么作图问题呢? 作线段的垂直平分线 我们已能用尺规完成: 作线段的垂直平分线 例1 如图,点A 和点B 关于某条直线成轴对称,
你能作出这条直线吗?
这种作图方法还有哪些作用?
确定线段的中点. 作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径
作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线. 作线段的垂直平分线 怎样作线段AB 的垂直平分线呢? 作轴对称图形的对称轴 如果两个图形成轴对称,怎样作出图形的对称轴? 如果两个图形成轴对称,其对称轴是任何一对对应
点所连线段的垂直平分线.因此,只要找到任意一组对
应点,作出对应点所连线段的垂直平分线,就得到此图
形的对称轴.作轴对称图形或两个图形成轴对称的对称轴的方法1,找点(找出任意一组对称点)
2,连线(连接这组对称点)
3,画出对称点所连线段的垂直平分线作轴对称图形的对称轴 如图中的五角星,请作出它的一条对称轴. 五角星的对称轴有什么特点? 作轴对称图形的对称轴 你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?相交于一点. 课堂练习 练习1 作出下列图形的一条对称轴,和同学比较
一下,你们作出的对称轴一样吗?课堂练习 练习2 如图,角是轴对称图形吗?如果是,它的
对称轴是什么?课堂练习 练习3 如图,与图形A 成轴对称的是哪个图形?
画出它的对称轴. 你能用不同的方法验证
这一结论吗?探索并证明线段垂直平分线的性质 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系. 相等. 探索并证明线段垂直平分线的性质 请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条
线段两个端点的距离相等. 已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.探索并证明线段垂直平分线的性质 证明:“线段垂直平分线上的点到线段两端点的距
离相等.”探索并证明线段垂直平分线的性质用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB. 证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.探索并证明线段垂直平分线的性质 线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离
相等.8课堂练习 练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平
分线上,
∴ AC =CE.课堂练习 练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?课堂练习 练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系? 解: ∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .探索并证明线段垂直平分线的判定 反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢? 点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.探索并证明线段垂直平分线的判定证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.探索并证明线段垂直平分线的判定 用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上. 这些点能组成什么几何图形? 探索并证明线段垂直平分线的判定 你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.课堂练习 练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?(1)为什么任意取一点K ,使点K与点C 在直线两旁?尺规作图 如何用尺规作图的方法经过直线外一点作已知直线
的垂线?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 12.1 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线www.12999.com课堂练习 练习4 如图,过点P 画∠AOB 两边的垂线,并和
同桌交流你的作图过程.
2、如图,其中是轴对称图形的是( )
3、图中的图形中是常见的安全标记,其中是轴对称图形的是 ( )
BAC7、如图所示的图案中,是轴对称图形且有两条
对称轴的是( )
6、下列图形中一定是轴对称图形的是 ( )
A、梯形 B、直角三角形? C、角 D、平行四边形CD5、下列英文字母属于轴对称图形的是( )
A、N B、S C、L D、ED9、如图所示的标志中,不是轴对称图形的有( )
A B C D
10、如图是用纸折叠成的图案,其中不是轴对称图形的有( )
(1)
CD
一个平面图形互相重合轴对称图形对称轴定 义课堂练习 练习1 如图所示的每个图形是轴对称图形吗?如
果是,指出它的对称轴. (1)有些轴对称图形的对称轴只有一条,但有的轴对称图形的对称轴却不止一条,有的轴对称图形的对称轴甚至有无数条。 (2)对称轴通常画成虚线,是直线,不能画成线段。对称轴问题下面两个图形有什么共同特点?1.把_______沿着某一条直线折叠,如果它能够与_____图形____,那么就说这两个图形______________或者说这两个图形成轴对称。
2.同样,我们把这条直线叫做______.
3.折叠后重合的点是对应点,叫做______.一个图形另一个重合关于这条直线对称对称轴对称点定义ABCA′B′C′对称点D D′对称轴做P60页第二题 下列给出的每幅图形中的两个图案是轴对称吗?如果是,试着找出它们的对称轴。喜喜FF(A)(C)(B)练习:不是轴对称图形两个图形成轴对称想一想想一想:1、对两个图形而言
2、指两个图形的相互关系
3、只有一条对称轴1、对一个图形而言
2、指一个图形的特殊形状
3、至少有一条对称轴1、沿某条直线对折后,直线两旁的部分都能重合;
2、若将成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形;若把轴对称图形沿对称轴看成两个图形,那么这两个图形关于这条对称轴成轴对称.
3.都有对称轴复习线段的垂线和线段的中点
线段垂直平分线的定义探索新知 问题3 如图,△ABC 和△A′B′C′关于直线MN
对称,点A′,B′,C′分别是点A,B,C 的对称点,线
段AA′,BB′,CC′与直线MN 有什么关系? 成轴对称的两个图形的性质:
如果两个图形关于某条
直线对称,那么对称轴是任
何一对对应点所连线段的垂
直平分线.即对称点所连线
段被对称轴垂直平分;对称
轴垂直平分对称点所连线段. Ho 轴对称图形的性质:
轴对称图形的对称轴,是任何
一对对应点所连线段的垂直平分线. 探索新知 问题4 下图是一个轴对称图形,你能发现什么结
论?能说明理由吗? NPo 不折叠图形,你能准确地作出轴对称图形的对称
轴吗? 作线段的垂直平分线 有时我们感觉两个平面图形是轴对称的,如何验
证呢?喜喜(1)作一条线段等于已知线段;
(2)作一个角等于已知角;
(3)作一个角的平分线;
那么利用尺规还能解决什么作图问题呢? 作线段的垂直平分线 我们已能用尺规完成: 作线段的垂直平分线 例1 如图,点A 和点B 关于某条直线成轴对称,
你能作出这条直线吗?
这种作图方法还有哪些作用?
确定线段的中点. 作法:如图.
(1)分别以点A,B 为圆心,以大于 AB的长为半径
作弧,两弧相交于C,D 两点;
(2)作直线CD.
CD 就是所求作的直线. 作线段的垂直平分线 怎样作线段AB 的垂直平分线呢? 作轴对称图形的对称轴 如果两个图形成轴对称,怎样作出图形的对称轴? 如果两个图形成轴对称,其对称轴是任何一对对应
点所连线段的垂直平分线.因此,只要找到任意一组对
应点,作出对应点所连线段的垂直平分线,就得到此图
形的对称轴.作轴对称图形或两个图形成轴对称的对称轴的方法1,找点(找出任意一组对称点)
2,连线(连接这组对称点)
3,画出对称点所连线段的垂直平分线作轴对称图形的对称轴 如图中的五角星,请作出它的一条对称轴. 五角星的对称轴有什么特点? 作轴对称图形的对称轴 你能作出这个五角星的其他对称轴吗?它共有几条
对称轴?相交于一点. 课堂练习 练习1 作出下列图形的一条对称轴,和同学比较
一下,你们作出的对称轴一样吗?课堂练习 练习2 如图,角是轴对称图形吗?如果是,它的
对称轴是什么?课堂练习 练习3 如图,与图形A 成轴对称的是哪个图形?
画出它的对称轴. 你能用不同的方法验证
这一结论吗?探索并证明线段垂直平分线的性质 如图,直线l 垂直平分线段AB,P1,P2,P3,…是
l 上的点,请猜想点P1,P2,P3,… 到点A 与点B 的距
离之间的数量关系. 相等. 探索并证明线段垂直平分线的性质 请在图中的直线l 上任取一点,那么这一点与线段
AB 两个端点的距离相等吗? 线段垂直平分线上的点与这条
线段两个端点的距离相等. 已知:如图,直线l⊥AB,垂足为C,AC =CB,点
P 在l 上.
求证:PA =PB.探索并证明线段垂直平分线的性质 证明:“线段垂直平分线上的点到线段两端点的距
离相等.”探索并证明线段垂直平分线的性质用符号语言表示为:
∵ CA =CB,l⊥AB,
∴ PA =PB. 证明:∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.探索并证明线段垂直平分线的性质 线段垂直平分线的性质:
线段垂直平分线上的点与这条线段两个端点的距离
相等.8课堂练习 练习1 如图,在△ABC 中,BC =8,AB 的中垂线
交BC于D,AC 的中垂线交BC 与E,则△ADE 的周长等
于______.
解:∵ AD⊥BC,BD =DC,
∴ AD 是BC 的垂直平分线,
∴ AB =AC.
∵ 点C 在AE 的垂直平
分线上,
∴ AC =CE.课堂练习 练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系?课堂练习 练习2 如图,AD⊥BC,BD =DC,点C 在AE 的
垂直平分线上,AB,AC,CE 的长度有什么关系?
AB+BD与DE 有什么关系? 解: ∴ AB =AC =CE.
∵ AB =CE,BD =DC,
∴ AB +BD =CD +CE.
即 AB +BD =DE .探索并证明线段垂直平分线的判定 反过来,如果PA =PB,那么点P 是否在线段AB 的
垂直平分线上呢? 点P 在线段AB 的垂直平分线上. 已知:如图,PA =PB.
求证:点P 在线段AB 的垂直平
分线上.探索并证明线段垂直平分线的判定证明:过点P 作线段AB 的垂线PC,
垂足为C.则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
∵ PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.探索并证明线段垂直平分线的判定 用数学符号表示为:
∵ PA =PB,
∴ 点P 在AB 的垂直平分线上. 与一条线段两个端点距离相
等的点,在这条线段的垂直平分
线上. 这些点能组成什么几何图形? 探索并证明线段垂直平分线的判定 你能再找一些到线段AB 两端点的距离相等的点吗?
能找到多少个到线段AB 两端点距离相等的点? 在线段AB 的垂直平分线l 上的
点与A,B 的距离都相等;反过来,
与A,B 的距离相等的点都在直线l
上,所以直线l 可以看成与两点A、
B 的距离相等的所有点的集合.解:∵ AB =AC,
∴ 点A 在BC 的垂直平分线.
∵ MB =MC,
∵ 点M 在BC 的垂直平分线上,
∴ 直线AM 是线段BC 的垂直
平分线.课堂练习 练习3 如图,AB =AC,MB =MC.直线AM 是线段
BC 的垂直平分线吗?(1)为什么任意取一点K ,使点K与点C 在直线两旁?尺规作图 如何用尺规作图的方法经过直线外一点作已知直线
的垂线?(2)为什么要以大于 的长为半径作弧? (3)为什么直线CF 就是所求作的垂线?定理1 在角的平分线上的点到这个角的两边的距离相等。定理2 到一个角的两边的距离相等的点,在这个角的平分线上。 角的平分线是到角的两边距离相等的所有点的集合 12.1 线段的垂直平分线定 理 线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理 和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。 线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线www.12999.com课堂练习 练习4 如图,过点P 画∠AOB 两边的垂线,并和
同桌交流你的作图过程.
2、如图,其中是轴对称图形的是( )
3、图中的图形中是常见的安全标记,其中是轴对称图形的是 ( )
BAC7、如图所示的图案中,是轴对称图形且有两条
对称轴的是( )
6、下列图形中一定是轴对称图形的是 ( )
A、梯形 B、直角三角形? C、角 D、平行四边形CD5、下列英文字母属于轴对称图形的是( )
A、N B、S C、L D、ED9、如图所示的标志中,不是轴对称图形的有( )
A B C D
10、如图是用纸折叠成的图案,其中不是轴对称图形的有( )
(1)
CD
