广东省2015中考数学冲刺复习课件:第41课时 数形结合思想(共16张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第41课时 数形结合思想(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 826.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 13:57:57 | ||
图片预览






文档简介
课件16张PPT。数学
第41课时 数形结合思想第41课时 数形结合思想知识考点?对应精练
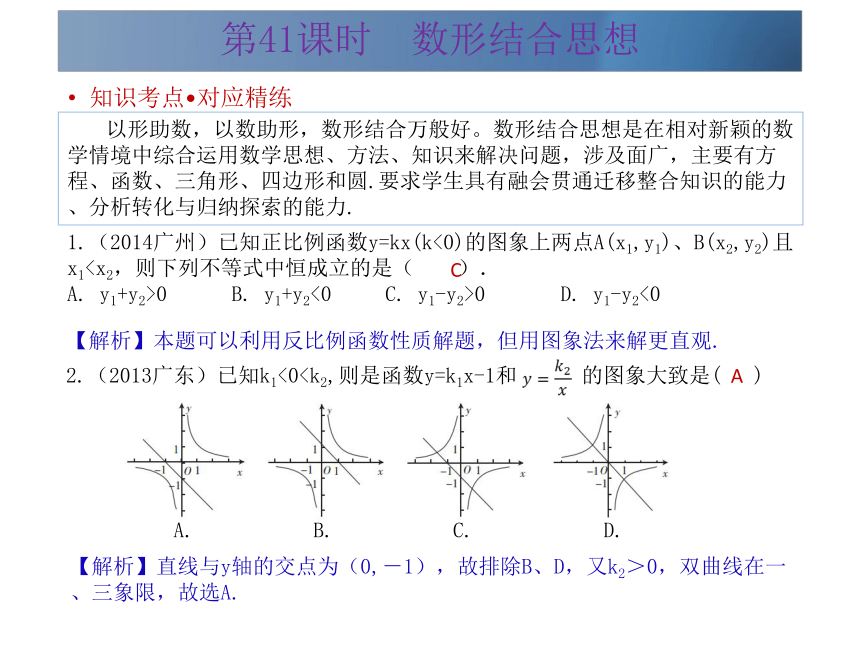
以形助数,以数助形,数形结合万般好。数形结合思想是在相对新颖的数学情境中综合运用数学思想、方法、知识来解决问题,涉及面广,主要有方程、函数、三角形、四边形和圆. 要求学生具有融会贯通迁移整合知识的能力、分析转化与归纳探索的能力.1.(2014广州)已知正比例函数y=kx(k<0)的图象上两点A(x1,y1)、B(x2,y2)且x1A. y1+y2>0 B. y1+y2<0 C. y1-y2>0 D. y1-y2<0【解析】本题可以利用反比例函数性质解题,但用图象法来解更直观.C2.(2013广东)已知k1<0 A. B. C. D.?A【解析】直线与y轴的交点为(0,-1),故排除B、D,又k2>0,双曲线在一、三象限,故选A.第41课时 数形结合思想 3.(2014广东佛山)利用二次函数的图象估计一元二次方程x2﹣2x﹣1=0的近似根(精确到0.1).【解析】根据函数与方程的关系,可得函数图象与x轴的交点的横坐标就是相应的方程的解.
解:∵二次函数y=x2﹣2x﹣1中a=1>0,
∴抛物线开口方向向上,
∴对称轴为
画出二次函数的图象:
根据图象与x轴的交点,得x2﹣2x﹣1=0的近似根x1=﹣0.4,x2=2.4.?第41课时 数形结合思想 4.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.【解析】(1)根据题意得出长×宽=192,进而得出答案;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,再利用二次函数增减性得出答案.
解:(1)∵AB=xm,则BC=(28-x)m,
∴x(28-x)=192,
解得:x1=12,x2=16,
答:x的值为12m或16m;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,
∴ x=15时,S取到最大值为:S=-(15-14)2+196=195,
答:花园面积S的最大值为195平方米.第41课时 数形结合思想真题演练?层层推进
基础题1.(2013年广州市)实数a在数轴上的位置如图4所示,则│a-2.5│=( )
A. a-2.5 B. 2.5-a C. a+2.5 D. –a-2.52.(2012广东茂名)如果x<0,y>0,x+y<0,那么下列关系式中正确的是( )
A、x>y>―y>―x B、―x >y >―y >x
C、y>―x>―y>x D、―x >y > x >―y 3.(2013珠海)已知函数y=3x的图象经过点A(-1,y1)、点B(-2,y2),则y1 y2(填“>”或“<”或“=”).4.(2014年汕尾)已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限5.(2014佛山)如图是一副三角板叠放的示意图,则∠α= .BB>A75°第41课时 数形结合思想提高题6.(2014广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.对称轴是直线x=
C.当x< ,y随x的增大而减小 D.当 -10 ????【解析】从图象中,我们能看到抛物线开口向上,则有最小值;与x轴交于(-1,0)和(2,0)两点,则对称轴为 ;当x< 时,随x的增大而减小;当 -1【解析】构造两个直角三角形△ABE与△BDF,分别求解可得DF与EB的值,再利用图形关系,进而可求出答案.
∵BE:AE=5:12, =13,
∴BE:AE:AB=5:12:13,
∵AB=1300米,
∴AE=1200米,BE=500米,
设EC=x米,
∵∠DBF=60°,
∴DF= x米.
又∵∠DAC=30°,
∴AC= CD.
即:1200+x= (500+ x),
解得 =600﹣250 .
∴DF= x=600 ﹣750,
∴CD=DF+CF=600 ﹣250(米).?????????B第41课时 数形结合思想拔高题8.(2014广州)已知一次函数y=kx-6的图像与反比例函数 的图像交于A、B两点,点A的横坐标为2.
(1)求k的值和点A的坐标;
(2)判断点B的象限,并说明理由.?解:(1)将y=kx-6与 联立得: ,∴ ,
A点是两个函数图象交点,将x=2代入上式得:
解得k=2
故一次函数解析式为y=2x-6,反比例函数解析式为:
将x=2代入y=2x-6,得y=2×2-6=-2,
A的坐标为(2,-2)
(2)B点在第四象限,理由如下:
一次函数y=2x-6经过第一、三、四象限,反比例函数经过第二、四象限,因此它们的交点都是在第四象限.
?????第41课时 数形结合思想课时作业一、选择题1.若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°?4.已知函数y=(x-m)(x-n)(其中m?DABC第41课时 数形结合思想课时作业 5.张华在一次数学活动中,利用“在面积一定的矩形中,正方形的周长最短”的结论,推导出“式子 (x>0)的最小值是2”.其推导方法如下:在面积是1的矩形中设矩形的一边长为x,则另一边长是 ,矩形的周长是 ;当矩形成为正方形时,就有 (x>0),解得x=1,这时矩形的周长 最小,因此 (x>0)的最小值是2.模仿张华的推导,你求得式子 (x>0)的最小值是( )
A. 2 B. 1 C. 6 D. 10?????????C二、填空题6.一只自由飞行的小鸟, 将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .7.如图,已知函数y=2x+b与函数y=kx-3的图像交于点P,则不等式kx-3>2x+b的解集是 .第41课时 数形结合思想课时作业 8.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .9.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,则选取点B为坐标原点时的抛物线解析式是 .10.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .??5?第41课时 数形结合思想课时作业三、解答题11.如图,在矩形ABCD中, ,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE?ED= ,求矩形ABCD的面积.??解:如图,连接BE,则BE=BC.设AB=3x,BC=5x,
∵四边形ABCD是矩形,
∴AB=CD=3x,AD=BC=5x,∠A=90°,
由勾股定理得:AE= =4x,则DE=x,
∵AE*ED= ,即4x*x= ,
解得:x= 或x=- (不合题意,舍去)
则AB=3x= ,BC=5x= ,
∴矩形ABCD的面积是AB×BC= =5.????????第41课时 数形结合思想课时作业 12.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?解:(1)由图可知,A比B后出发1小时;B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设直线OC的解析式为y=kx,则3k=60,
解得k=20,
∴直线OC的解析式为y=20x,
设直线DE的解析式为y=mx+n,则 ,
解得 m=45,n=-45,
∴直线DE的解析式为y=45x-45,
解方程组 ,得 ,
∴在B出发 小时后,两人相遇.????第41课时 数形结合思想课时作业 13.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少 ?小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.解:(1)设矩形的边长PN=2ymm,则PQ=ymm,由条件可得△APN∽△ABC,
∴ ,即 ,解得 ,
∴ ,
答:这个矩形零件的两条边长分别为 , ;
(2)设PN=xmm,由条件可得△APN∽△ABC,
∴ ,即 ,
解得 ,
∴
∴S的最大值为2400mm2,此时PN=60mm,PQ=40mm.??????????第41课时 数形结合思想课时作业 14.如图,点A(m,6),B(n,1)在反比例函数图像上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5,若存在,求出E点坐标;若不存在,请说明理由.解:(1)由题意,得 ,解得 ,
∴m,n的值分别为1,6.
设反比例函数关系式为 ,
∴k=1×6=6,∴ ;
(2)存在,理由如下:
设E(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,∴∠ADE=∠BCE=90°,
如图,连接AE,BE,
△ABE的面积
∴x=5,即E(5,0).?????结束谢谢!
以形助数,以数助形,数形结合万般好。数形结合思想是在相对新颖的数学情境中综合运用数学思想、方法、知识来解决问题,涉及面广,主要有方程、函数、三角形、四边形和圆. 要求学生具有融会贯通迁移整合知识的能力、分析转化与归纳探索的能力.1.(2014广州)已知正比例函数y=kx(k<0)的图象上两点A(x1,y1)、B(x2,y2)且x1
解:∵二次函数y=x2﹣2x﹣1中a=1>0,
∴抛物线开口方向向上,
∴对称轴为
画出二次函数的图象:
根据图象与x轴的交点,得x2﹣2x﹣1=0的近似根x1=﹣0.4,x2=2.4.?第41课时 数形结合思想 4.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为192m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.【解析】(1)根据题意得出长×宽=192,进而得出答案;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,再利用二次函数增减性得出答案.
解:(1)∵AB=xm,则BC=(28-x)m,
∴x(28-x)=192,
解得:x1=12,x2=16,
答:x的值为12m或16m;
(2)由题意可得出:S=x(28-x)=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,
∴ x=15时,S取到最大值为:S=-(15-14)2+196=195,
答:花园面积S的最大值为195平方米.第41课时 数形结合思想真题演练?层层推进
基础题1.(2013年广州市)实数a在数轴上的位置如图4所示,则│a-2.5│=( )
A. a-2.5 B. 2.5-a C. a+2.5 D. –a-2.52.(2012广东茂名)如果x<0,y>0,x+y<0,那么下列关系式中正确的是( )
A、x>y>―y>―x B、―x >y >―y >x
C、y>―x>―y>x D、―x >y > x >―y 3.(2013珠海)已知函数y=3x的图象经过点A(-1,y1)、点B(-2,y2),则y1 y2(填“>”或“<”或“=”).4.(2014年汕尾)已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限5.(2014佛山)如图是一副三角板叠放的示意图,则∠α= .BB>A75°第41课时 数形结合思想提高题6.(2014广东)二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.对称轴是直线x=
C.当x< ,y随x的增大而减小 D.当 -1
∵BE:AE=5:12, =13,
∴BE:AE:AB=5:12:13,
∵AB=1300米,
∴AE=1200米,BE=500米,
设EC=x米,
∵∠DBF=60°,
∴DF= x米.
又∵∠DAC=30°,
∴AC= CD.
即:1200+x= (500+ x),
解得 =600﹣250 .
∴DF= x=600 ﹣750,
∴CD=DF+CF=600 ﹣250(米).?????????B第41课时 数形结合思想拔高题8.(2014广州)已知一次函数y=kx-6的图像与反比例函数 的图像交于A、B两点,点A的横坐标为2.
(1)求k的值和点A的坐标;
(2)判断点B的象限,并说明理由.?解:(1)将y=kx-6与 联立得: ,∴ ,
A点是两个函数图象交点,将x=2代入上式得:
解得k=2
故一次函数解析式为y=2x-6,反比例函数解析式为:
将x=2代入y=2x-6,得y=2×2-6=-2,
A的坐标为(2,-2)
(2)B点在第四象限,理由如下:
一次函数y=2x-6经过第一、三、四象限,反比例函数经过第二、四象限,因此它们的交点都是在第四象限.
?????第41课时 数形结合思想课时作业一、选择题1.若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°?4.已知函数y=(x-m)(x-n)(其中m
A. 2 B. 1 C. 6 D. 10?????????C二、填空题6.一只自由飞行的小鸟, 将随意地落在如图所示的方格地面上,每个小方格形状完全相同,则小鸟落在阴影方格地面上的概率是 .7.如图,已知函数y=2x+b与函数y=kx-3的图像交于点P,则不等式kx-3>2x+b的解集是 .第41课时 数形结合思想课时作业 8.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 .9.如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是 ,则选取点B为坐标原点时的抛物线解析式是 .10.网格中的每个小正方形的边长都是1,△ABC每个顶点都在网格的交点处,则sinA= .??5?第41课时 数形结合思想课时作业三、解答题11.如图,在矩形ABCD中, ,以点B为圆心,BC长为半径画弧,交边AD于点E.若AE?ED= ,求矩形ABCD的面积.??解:如图,连接BE,则BE=BC.设AB=3x,BC=5x,
∵四边形ABCD是矩形,
∴AB=CD=3x,AD=BC=5x,∠A=90°,
由勾股定理得:AE= =4x,则DE=x,
∵AE*ED= ,即4x*x= ,
解得:x= 或x=- (不合题意,舍去)
则AB=3x= ,BC=5x= ,
∴矩形ABCD的面积是AB×BC= =5.????????第41课时 数形结合思想课时作业 12.已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?解:(1)由图可知,A比B后出发1小时;B的速度:60÷3=20(km/h);
(2)由图可知点D(1,0),C(3,60),E(3,90),
设直线OC的解析式为y=kx,则3k=60,
解得k=20,
∴直线OC的解析式为y=20x,
设直线DE的解析式为y=mx+n,则 ,
解得 m=45,n=-45,
∴直线DE的解析式为y=45x-45,
解方程组 ,得 ,
∴在B出发 小时后,两人相遇.????第41课时 数形结合思想课时作业 13.课本中有一道作业题:有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少 ?小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.解:(1)设矩形的边长PN=2ymm,则PQ=ymm,由条件可得△APN∽△ABC,
∴ ,即 ,解得 ,
∴ ,
答:这个矩形零件的两条边长分别为 , ;
(2)设PN=xmm,由条件可得△APN∽△ABC,
∴ ,即 ,
解得 ,
∴
∴S的最大值为2400mm2,此时PN=60mm,PQ=40mm.??????????第41课时 数形结合思想课时作业 14.如图,点A(m,6),B(n,1)在反比例函数图像上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)求m,n的值并写出反比例函数的表达式;
(2)连接AB,在线段DC上是否存在一点E,使△ABE的面积等于5,若存在,求出E点坐标;若不存在,请说明理由.解:(1)由题意,得 ,解得 ,
∴m,n的值分别为1,6.
设反比例函数关系式为 ,
∴k=1×6=6,∴ ;
(2)存在,理由如下:
设E(x,0),则DE=x-1,CE=6-x,
∵AD⊥x轴,BC⊥x轴,∴∠ADE=∠BCE=90°,
如图,连接AE,BE,
△ABE的面积
∴x=5,即E(5,0).?????结束谢谢!
同课章节目录
