广东省2015中考数学冲刺复习课件:第40课时 分类思想(共14张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第40课时 分类思想(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 13:58:58 | ||
图片预览






文档简介
课件14张PPT。数学
第40课时 分类思想第40课时 分类思想知识考点?对应精练 分类思想初中数学主要的数学思想方法,根据研究对象性质的差异,分各种不同情况进行讨论。而产生分类的因素很多:由数学概念、性质、定理的限制条件引起讨论;由数学变形所需要的限制条件所引起的讨论;由于图形的不确定性引起讨论;由于题目条件开放或结论引起讨论。分类必须遵循不遗漏且不重复的原则。?【解析】本题需分类讨论:对于一元一次方程在一次项系数不为0时有唯一解,而一元二次方程根的情况由根的判别式确定【答案】C.第40课时 分类思想 2.如图,在矩形ABCD中,AB=4,BC=6,若点P在AD边上,连接BP、PC,△BPC是以PB为腰的等腰三角形,则PB的长为 .【解析】等腰三角形的分类讨论:PB=PC和PB=BC两种情况.?第40课时 分类思想 3.如图矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D′落在∠ABC的角平分线上时,DE的长为 .?第40课时 分类思想真题演练?层层推进
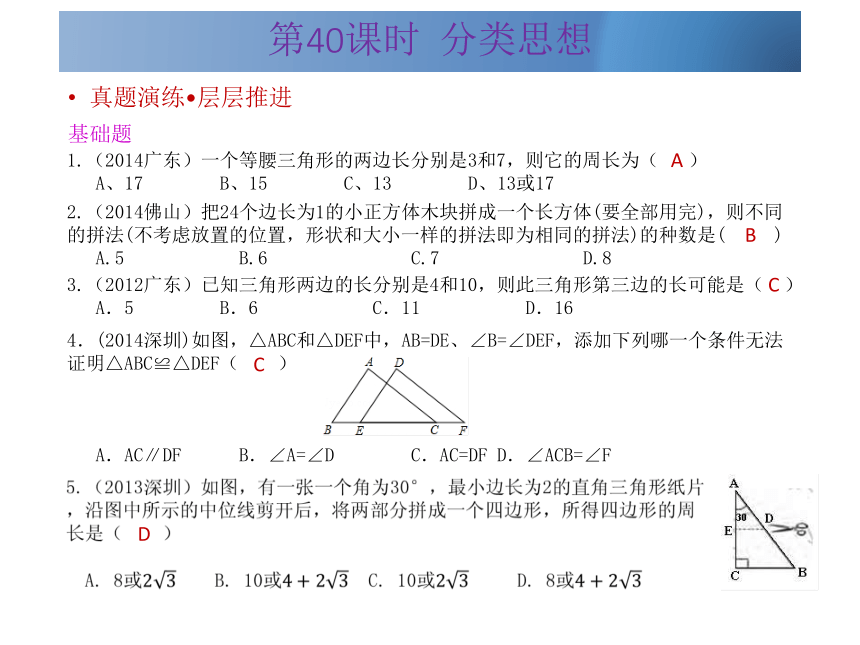
基础题1.(2014广东)一个等腰三角形的两边长分别是3和7,则它的周长为( )
A、17 B、15 C、13 D、13或172.(2014佛山)把24个边长为1的小正方体木块拼成一个长方体(要全部用完),则不同的拼法(不考虑放置的位置,形状和大小一样的拼法即为相同的拼法)的种数是( )
A.5 B.6 C.7 D.84.(2014深圳)如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F3.(2012广东)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16?DCCBA第40课时 分类思想提高题6.(2014佛山)现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等式的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).解:(1)a>0时,a+a>a+0,即2a>a, a<0时,a+a<a+0,即2a<a;
(2)a>0时,2>1,即2a>a; a<0时,2>1,即2a<a.7.(2014珠海)为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?解:(1)方案一:y=0.95x;
方案二:y=0.9x+300;
(2)当x=5880时,方案一:y=0.95x=5586,
方案二:y=0.9x+300=5592,
∵5586<5592
∴选择方案一更省钱.第40课时 分类思想拔高题?第40课时 分类思想 ?第40课时 分类思想课时作业一、选择题1.已知线段AB=8 cm,在直线AB上画线段BC,使BC=5 cm,则线段AC的长度为( )
A.3 cm或13 cm B.3 cm C.13 cm D.18 cm2.如果一个等腰三角形的两边长分别是5 cm和6 cm,那么此三角形的周长是( )
A.15 cm B.16 cm C.17 cm D.16 cm或17 cm3.如图,反比例函数 和正比例函数 的图象交于A ,B(1,3)两点,若 ,则x的取值范围是( )
A.-1<x<0 B.-1<x<1
C.x<-1或0<x<1 D.-1<x<0或x>1???4.当a≠0时,函数y=ax+1与函数 在同一坐标系中的图象可能是( )
A B C D?5.在直径为10cm的⊙O中,弦AB=8cm,弦CD=6cm,且AB∥CD,则AB与CD之间的距离是( )
A.7cm B.1cm C.7cm或1cm D.3cm或4cmACDCC第40课时 分类思想课时作业二、填空题6.若等腰三角形的两条边长分别为7cm和14cm,则它的周长为 cm.7.等腰三角形一腰上的高与另一腰的夹角为36,则该等腰三角形的底角的度数为 .?9.过反比例函数 (k≠0)图象上的一点A,分别作x轴、y轴的垂线,垂足分别为B,C.若△ABC的面积为3,则k的值为________.??10.设抛物线 过A(0,2), B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线对称轴的距离等于1,则抛物线的函数思路分析式为 .?3563°或27°60°或120°±6?第40课时 分类思想课时作业三、解答题 11.一次函数y=x+4分别交x轴、y轴于A、B两点,C为坐标轴上一点,且△ABC为等腰三角形,求点C的坐标.解:∵当x=0时,y=4 ,当y=0时,x=-4 ,
∴A(-4,0),B(0,4) ,
∴AB= ,
要使△ABC是等腰三角形,还应分三种情况讨论:
①当AB=AC时,点C的坐标为(- -4,0)或( -4,0) ;
②当BA=BC时,点C的坐标为 (4,0);
③当AC=BC时,点C的坐标为(0,0) ;
综上所述,点C坐标为(- -4,0)或( -4,0)或(4,0)或(0,0).?????第40课时 分类思想课时作业 12.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?解:(1)设生产A种产品x件,则生产B种产品(10-x)件,
得x=2(10-x)=14,解得x=6
∴10-x=10-6=4(件)
答:生产A种产品6件,B种产品4件.
(2)设生产A种产品x件,则生产B种产品(10-x)件,
得 ;解得3≤x<6
又∵x为整数,
∴x的值可为3或4或5
∴共有三种方案:
①生产A种产品3件,B种产品7件;
②生产A种产品4件,B种产品6件;
③生产A种产品5件,B种产品5件.?第40课时 分类思想课时作业 13.如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5.
(1)如图①,若点P是 的中点,求PA的长;
(2)如图②,若点P是的 中点,求PA的长.解:(1)如图(1)所示,连接PB,
∵AB是⊙O的直径且P是 的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△ABC中有AB=13,
∴PA= ;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,∴OP⊥BC,∠OMB=90°,
又因为AB为直径,∴∠ACB=90°,∴∠ACB=∠OMB,
∴OP∥AC,∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,∴△ACB∽△0NP
∴ ,
又∵AB=13 AC=5 OP= ,代入得 ON= ,
∴AN=OA+ON=9 ∴在Rt△OPN中,有
在Rt△ANP中 有PA= = ∴PA= .????????结束谢谢!
基础题1.(2014广东)一个等腰三角形的两边长分别是3和7,则它的周长为( )
A、17 B、15 C、13 D、13或172.(2014佛山)把24个边长为1的小正方体木块拼成一个长方体(要全部用完),则不同的拼法(不考虑放置的位置,形状和大小一样的拼法即为相同的拼法)的种数是( )
A.5 B.6 C.7 D.84.(2014深圳)如图,△ABC和△DEF中,AB=DE、∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A.AC∥DF B.∠A=∠D C.AC=DF D.∠ACB=∠F3.(2012广东)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A.5 B.6 C.11 D.16?DCCBA第40课时 分类思想提高题6.(2014佛山)现有不等式的性质:
①在不等式的两边都加上(或减去)同一个整式,不等号的方向不变;
②在不等式的两边都乘以同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等式的方向改变.
请解决以下两个问题:
(1)利用性质①比较2a与a的大小(a≠0);
(2)利用性质②比较2a与a的大小(a≠0).解:(1)a>0时,a+a>a+0,即2a>a, a<0时,a+a<a+0,即2a<a;
(2)a>0时,2>1,即2a>a; a<0时,2>1,即2a<a.7.(2014珠海)为庆祝商都正式营业,商都推出了两种购物方案.方案一:非会员购物所有商品价格可获九五折优惠,方案二:如交纳300元会费成为该商都会员,则所有商品价格可获九折优惠.
(1)以x(元)表示商品价格,y(元)表示支出金额,分别写出两种购物方案中y关于x的函数解析式;
(2)若某人计划在商都购买价格为5880元的电视机一台,请分析选择哪种方案更省钱?解:(1)方案一:y=0.95x;
方案二:y=0.9x+300;
(2)当x=5880时,方案一:y=0.95x=5586,
方案二:y=0.9x+300=5592,
∵5586<5592
∴选择方案一更省钱.第40课时 分类思想拔高题?第40课时 分类思想 ?第40课时 分类思想课时作业一、选择题1.已知线段AB=8 cm,在直线AB上画线段BC,使BC=5 cm,则线段AC的长度为( )
A.3 cm或13 cm B.3 cm C.13 cm D.18 cm2.如果一个等腰三角形的两边长分别是5 cm和6 cm,那么此三角形的周长是( )
A.15 cm B.16 cm C.17 cm D.16 cm或17 cm3.如图,反比例函数 和正比例函数 的图象交于A ,B(1,3)两点,若 ,则x的取值范围是( )
A.-1<x<0 B.-1<x<1
C.x<-1或0<x<1 D.-1<x<0或x>1???4.当a≠0时,函数y=ax+1与函数 在同一坐标系中的图象可能是( )
A B C D?5.在直径为10cm的⊙O中,弦AB=8cm,弦CD=6cm,且AB∥CD,则AB与CD之间的距离是( )
A.7cm B.1cm C.7cm或1cm D.3cm或4cmACDCC第40课时 分类思想课时作业二、填空题6.若等腰三角形的两条边长分别为7cm和14cm,则它的周长为 cm.7.等腰三角形一腰上的高与另一腰的夹角为36,则该等腰三角形的底角的度数为 .?9.过反比例函数 (k≠0)图象上的一点A,分别作x轴、y轴的垂线,垂足分别为B,C.若△ABC的面积为3,则k的值为________.??10.设抛物线 过A(0,2), B(4,3),C三点,其中点C在直线x=2上,且点C到抛物线对称轴的距离等于1,则抛物线的函数思路分析式为 .?3563°或27°60°或120°±6?第40课时 分类思想课时作业三、解答题 11.一次函数y=x+4分别交x轴、y轴于A、B两点,C为坐标轴上一点,且△ABC为等腰三角形,求点C的坐标.解:∵当x=0时,y=4 ,当y=0时,x=-4 ,
∴A(-4,0),B(0,4) ,
∴AB= ,
要使△ABC是等腰三角形,还应分三种情况讨论:
①当AB=AC时,点C的坐标为(- -4,0)或( -4,0) ;
②当BA=BC时,点C的坐标为 (4,0);
③当AC=BC时,点C的坐标为(0,0) ;
综上所述,点C坐标为(- -4,0)或( -4,0)或(4,0)或(0,0).?????第40课时 分类思想课时作业 12.某工厂计划生产A、B两种产品共10件,其生产成本和利润如下表:
(1)若工厂计划获利14万元,问A、B两种产品应分别生产多少件?
(2)若工厂投入资金不多于44万元,且获利多于14万元,问工厂有哪几种生产方案?解:(1)设生产A种产品x件,则生产B种产品(10-x)件,
得x=2(10-x)=14,解得x=6
∴10-x=10-6=4(件)
答:生产A种产品6件,B种产品4件.
(2)设生产A种产品x件,则生产B种产品(10-x)件,
得 ;解得3≤x<6
又∵x为整数,
∴x的值可为3或4或5
∴共有三种方案:
①生产A种产品3件,B种产品7件;
②生产A种产品4件,B种产品6件;
③生产A种产品5件,B种产品5件.?第40课时 分类思想课时作业 13.如图,AB是⊙O的直径,C,P是 上两点,AB=13,AC=5.
(1)如图①,若点P是 的中点,求PA的长;
(2)如图②,若点P是的 中点,求PA的长.解:(1)如图(1)所示,连接PB,
∵AB是⊙O的直径且P是 的中点,
∴∠PAB=∠PBA=45°,∠APB=90°,
又∵在等腰三角形△ABC中有AB=13,
∴PA= ;
(2)如图(2)所示:连接BC.OP相交于M点,作PN⊥AB于点N,
∵P点为弧BC的中点,∴OP⊥BC,∠OMB=90°,
又因为AB为直径,∴∠ACB=90°,∴∠ACB=∠OMB,
∴OP∥AC,∴∠CAB=∠POB,
又因为∠ACB=∠ONP=90°,∴△ACB∽△0NP
∴ ,
又∵AB=13 AC=5 OP= ,代入得 ON= ,
∴AN=OA+ON=9 ∴在Rt△OPN中,有
在Rt△ANP中 有PA= = ∴PA= .????????结束谢谢!
同课章节目录
