广东省2015中考数学冲刺复习课件:第38课时 几何动态综合题(共28张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第38课时 几何动态综合题(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 910.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:00:04 | ||
图片预览






文档简介
课件28张PPT。数学
第38课时 几何动态综合题第38课时 几何动态综合题知识考点?对应精练
【知识考点】
(1)动点问题;
(2)动线问题;
(3)动图问题.第38课时 几何动态综合题【对应精练】
1.如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图2所示,则线段EF所在的直线对应的函数关系式为 .【解析】再根据点E的纵坐标为9,当P为AD中点,
Q在B点时,△PAQ的面积为9,
可知9= ? AD?AB= AB2,所AB=AD=6.
可知P、Q分别运动6秒停止E(3,9),F(6,0).
设EF所在直线的解析式为:y=kx+b,
把E(3,9),F(6,0)代入就可以得出k=-3,b=18.
【答案】y=-3x+18y=-3x+18第38课时 几何动态综合题2.如图38-2,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值是 .6【解析】连接BD,DE,
由正方形的性质可知点B与点D关于直线AC对称,
故DE的长即为BQ+QE的最小值,进而可得出结论.
连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE= =5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
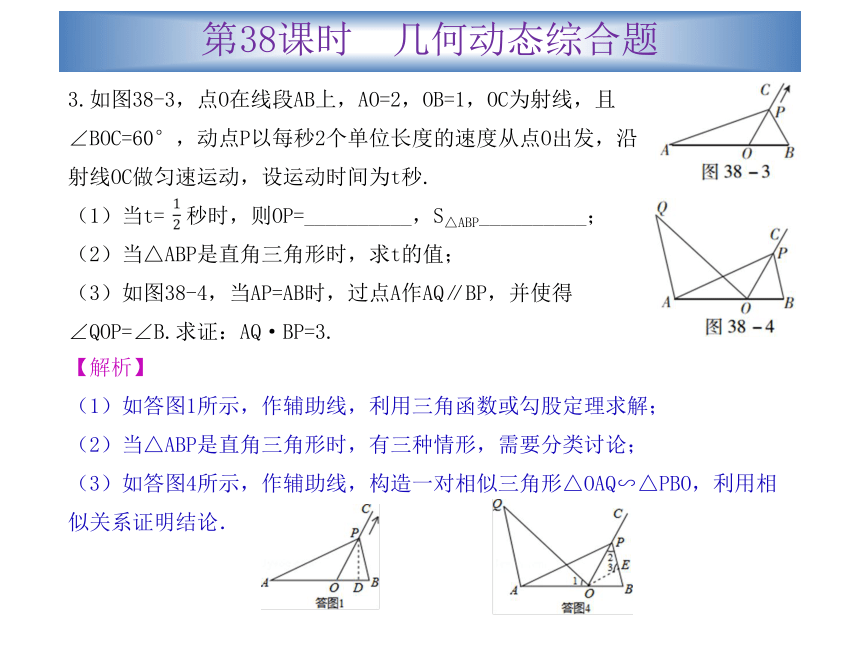
【答案】6第38课时 几何动态综合题3.如图38-3,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t= 秒时,则OP=__________,S△ABP__________;
(2)当△ABP是直角三角形时,求t的值;
(3)如图38-4,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B.求证:AQ·BP=3.【解析】
(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;
(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;
(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.第38课时 几何动态综合题【答案】
(1)当t= 秒时,OP=2t=2× =1.
如答图1,过点P作PD⊥AB于点D.
在Rt△POD中,PD=OP?sin60°=1× = ,
∴S△ABP= AB?PD= ×(2+1)× = . 第38课时 几何动态综合题【答案】
(2)解:当△ABP是直角三角形时,
①若∠A=90°.∵∠BOC=60°且∠BOC>∠A,
∴∠A≠90°,故此种情形不存在;
②若∠B=90°,如答图2所示:
∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=2,又OP=2t,∴t=1;
③若∠APB=90°,如答图3所示:过点P作PD⊥AB于点D,
则OD=OP?cos30°=t,PD=OP?sin60°= t,
∴AD=OA+OD=2+t,BD=OB﹣OD=1﹣t.
在Rt△ABP中,由勾股定理得:PA2+PB2=AB2
∴(AD2+PD2)+(BD2+PD2)=AB2,
即[(2+t)2+( t)2]+[(1﹣t)2+( t)2]=32
解方程得:t= ,或t= (负值舍去),∴t= ,
综上所述,当△ABP是直角三角形时,t=1或t= 第38课时 几何动态综合题【答案】
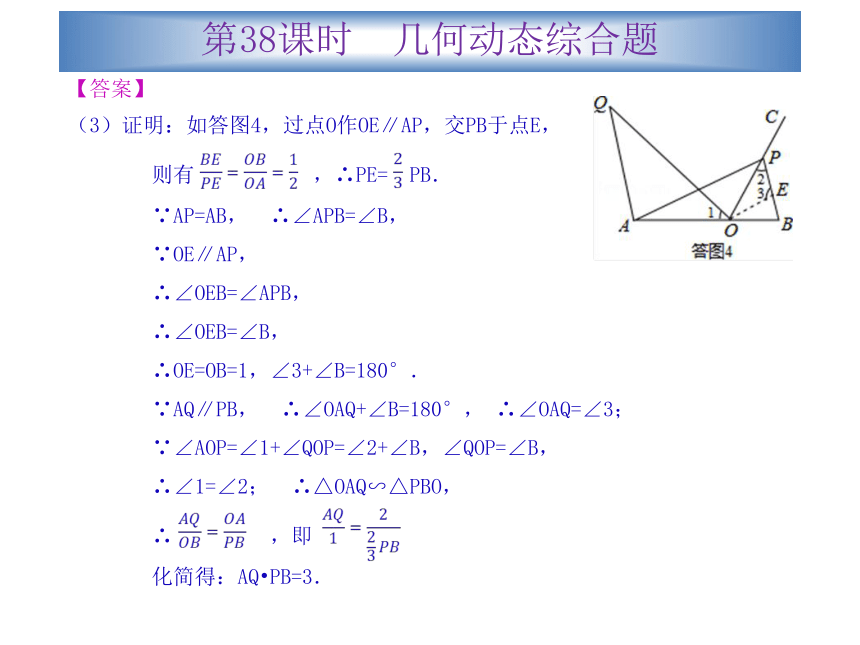
(3)证明:如答图4,过点O作OE∥AP,交PB于点E,
则有 ,∴PE= PB.
∵AP=AB, ∴∠APB=∠B,
∵OE∥AP,
∴∠OEB=∠APB,
∴∠OEB=∠B,
∴OE=OB=1,∠3+∠B=180°.
∵AQ∥PB, ∴∠OAQ+∠B=180°, ∴∠OAQ=∠3;
∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,
∴∠1=∠2; ∴△OAQ∽△PBO,
∴ ,即
化简得:AQ?PB=3.第38课时 几何动态综合题真题演练?层层推进
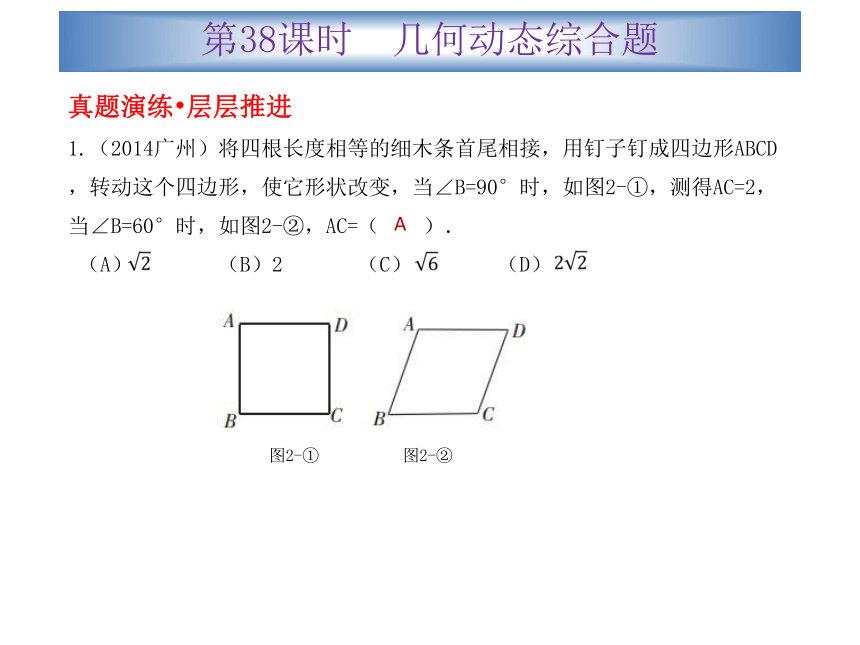
1.(2014广州)将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图2-①,测得AC=2,当∠B=60°时,如图2-②,AC=( ).
(A) (B)2 (C) (D) 图2-① 图2-② A第38课时 几何动态综合题2.(2014广东)如题25-1图,在△ABC中,AB=AC,AD⊥AB点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0)。
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值,若不存在,请说明理由。第38课时 几何动态综合题【答案】
(1)如图(1),连接DE,DF,
∵AB=AC,AD⊥BC, ∴BD=DC,
∵EF∥BC, ∴EF⊥AD,EH=FH,
∵t=2, ∴DH=4,
又AD=8,则AH=DH=4,
∴四边形AEDF是菱形;
(2)显然,BP=3t,DH=2t,则AH=8-2t,
∵EF∥BC, ∴ ,即 ,
∴EF= ,
设△PEF的面积为y,则
,即 ,
∴当t=2时,y有最大值为10,此时BP=6.第38课时 几何动态综合题【答案】
(3)存在满足条件的 ,理由如下:
如果△PEF是直角三角形,应分三种情况讨论:
① 当∠PEF=90°时,如图-1,则PE∥AD
所以 ,
此时,PE=DH=2t,BP=3t,
所以 ,解得t=0(舍去);
② 当∠EPF=90°时,如图-2,连接HP
则HP= EF= ,PD=│5-3t│
由勾股定理得,
解得 或t=0(舍去)
③ 当∠EFP=90°时,如图-3,则FP∥AD,
所以 ,即 ,解得 ,
综上所述,当 或 时,△PEF是直角三角形.第38课时 几何动态综合题3.(2013广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中, ∠FDE=90°,DF=4,DE= .将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,
则∠EMC=______度;
(2)如题25图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围.第38课时 几何动态综合题【答案】
(1)15;
(2)在Rt△CFA中,AC=6,∠ACF=∠E=30°,
∴FC= =6÷ ;(3)如图(4),设过点M作MN⊥AB于点N,则MN∥DE,∠NMB=∠B=45°,
∴NB=NM,NF=NB-FB=MN-x,∵MN∥DE,∴△FMN∽△FED,
∴ ,即 , ∴ ;
①当0≤x≤2时,如图(4) ,设DE与BC相交于点G ,则DG=DB=4+x,
∴ ,
即 ;第38课时 几何动态综合题【答案】
(3)②当 时,如图(5),
,
即 ;
③当 时, 如图(6) 设AC与EF交于点H,
∵AF=6-x,∠AHF=∠E=30°,∴AH= ,
;
综上所述,当 0≤x≤2 时, ,
当 时, ,
当 时, .第38课时 几何动态综合题课时作业一、选择题
1.如图,已知矩形ABCD的长AB为5,宽BC为4.E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点 E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )
2.如图,一根长为5米的竹竿AB斜立于墙AC的右侧,底端B与墙角C的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系 的大致图象是( )AA第38课时 几何动态综合题课时作业3.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC= ,∠B=60°,则CD的长为( )
A.0.4 B.1.5 C. D.14.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10) B.(-2,0)
C.(2,10)或(-2,0) D.(10,2)或(-2,0)5.如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连结AA′,若∠1=20°,
则∠B的度数是( )
A.70° B.65° C.60° D.55°DCB第38课时 几何动态综合题课时作业二、填空题
6.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆 时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,CA′相交于点D,则线段B D的长为 .7.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为 .8.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角. 当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,……第n次碰到矩形的边时的点为Pn. 则点P3的坐标是 ,点P2014的坐标是 .6(8,3)(5,0)第38课时 几何动态综合题课时作业9.如图,AB、CD是⊙O两条弦,AB=8,CD=6,MN是直径,AB⊥MN于E,CD⊥MN于点F,P为EF上任意一点,,则PA+PC的最小值为 .10.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD的中点,N是AB边上一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .第38课时 几何动态综合题课时作业三、解答题
11.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABEF是菱形.【答案】
(1)证明:∵ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
∴△ABD≌△ACE(SAS).第38课时 几何动态综合题课时作业【答案】
(2)解:∵∠CAE=100°,AC=AE,
∴∠ACE= ,
(3)证明:∵∠BAD=∠CAE=140°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=20°.
∵∠BAE=∠BAD+∠DAE=160°,
∴∠BFE=360°﹣∠DAE﹣∠ABD﹣∠AEC=160°,
∴∠BAE=∠BFE,
∴四边形ABEF是平行四边形,
∵AB=AE,
∴平行四边形ABEF是菱形.第38课时 几何动态综合题课时作业12.如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的 与线段CG所围成的阴影部分的面积.第38课时 几何动态综合题课时作业【答案】
(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°,
∵△BEC绕点B逆时针旋转90°得到△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,
∴∠AFB+∠FAB=90°,
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG,
∵AF=EC,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG;第38课时 几何动态综合题课时作业【答案】
(2)解:∵AD=2,E是AB的中点,
∴FE=BE= AB=1,
∴AF= ,
由平行四边形的性质,知△FEC≌△CGF,
∴S△FEC =S△CGF,
∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG
=
= .第38课时 几何动态综合题课时作业13.如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′ ,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.解:图中的所有的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,
理由如下:
∵四边形ABCD是正方形,
∴CD=AD=AB=BC,∠ADC=∠DAB=∠ABC=BCD=90°
由旋转的性质,知DC′=DC=AD=AB,∠DCC′=∠DC′C=75°,
∴△DC′C是等腰三角形
∵∠ADC =90°,∠CDC′=30°. ∴∠ADC′=60°
∵DC′=AD, ∴△DAC′为等边三角形
∴AC′=AD=AB,∠DAC′=∠DC′A=60°,
∴△ABC′为等腰三角形,∠BAC′=90°-60°=30°
∴∠ABC′=∠AC′B= (180°-30°)=75°
∴∠CBC′=90°-75°=15°,∠C′CB=90°-75°=15°
∴∠CBC′=∠C′CB. ∴△BCC′是等腰三角形.第38课时 几何动态综合题课时作业14.如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△DEF是直角三角形时,求x的值.【答案】
解:(1)∵在Rt△ABC中,∠B=90°,AC=60,AB=30,
∴∠C=30°,
∵CD=x,DF=y. ∴y= x ;
(2)∵四边形AEFD为菱形,
∴AD=DF, ∴y=60-x
解方程组 ,得x=40,y=20
∴当x=40时,四边形AEFD为菱形;第38课时 几何动态综合题课时作业【答案】
解:(3)∵△DEF是直角三角形,
∴∠FDE=90°,
∵FE∥AC,
∴∠EFB=∠C=30°,
∵DF⊥BC,
∴∠DEF+∠DFE=∠EFB+∠DFE,
∴∠DEF=∠EFB=30°,
∴EF=2DF,
∴60-x=2y ,
解方程组 ,得x=30 ,y=15.
∴当△DEF是直角三角形时,x=30.结束谢谢!
【知识考点】
(1)动点问题;
(2)动线问题;
(3)动图问题.第38课时 几何动态综合题【对应精练】
1.如图①,在正方形ABCD中,点P沿边DA从点D开始向点A以1cm/s的速度移动;同时,点Q沿边AB、BC从点A开始向点C以2cm/s的速度移动.当点P移动到点A时,P、Q同时停止移动.设点P出发xs时,△PAQ的面积为ycm2,y与x的函数图象如图2所示,则线段EF所在的直线对应的函数关系式为 .【解析】再根据点E的纵坐标为9,当P为AD中点,
Q在B点时,△PAQ的面积为9,
可知9= ? AD?AB= AB2,所AB=AD=6.
可知P、Q分别运动6秒停止E(3,9),F(6,0).
设EF所在直线的解析式为:y=kx+b,
把E(3,9),F(6,0)代入就可以得出k=-3,b=18.
【答案】y=-3x+18y=-3x+18第38课时 几何动态综合题2.如图38-2,在边长为4的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为对角线AC上的动点,则△BEQ周长的最小值是 .6【解析】连接BD,DE,
由正方形的性质可知点B与点D关于直线AC对称,
故DE的长即为BQ+QE的最小值,进而可得出结论.
连接BD,DE,
∵四边形ABCD是正方形,
∴点B与点D关于直线AC对称,
∴DE的长即为BQ+QE的最小值,
∵DE=BQ+QE= =5,
∴△BEQ周长的最小值=DE+BE=5+1=6.
【答案】6第38课时 几何动态综合题3.如图38-3,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.
(1)当t= 秒时,则OP=__________,S△ABP__________;
(2)当△ABP是直角三角形时,求t的值;
(3)如图38-4,当AP=AB时,过点A作AQ∥BP,并使得∠QOP=∠B.求证:AQ·BP=3.【解析】
(1)如答图1所示,作辅助线,利用三角函数或勾股定理求解;
(2)当△ABP是直角三角形时,有三种情形,需要分类讨论;
(3)如答图4所示,作辅助线,构造一对相似三角形△OAQ∽△PBO,利用相似关系证明结论.第38课时 几何动态综合题【答案】
(1)当t= 秒时,OP=2t=2× =1.
如答图1,过点P作PD⊥AB于点D.
在Rt△POD中,PD=OP?sin60°=1× = ,
∴S△ABP= AB?PD= ×(2+1)× = . 第38课时 几何动态综合题【答案】
(2)解:当△ABP是直角三角形时,
①若∠A=90°.∵∠BOC=60°且∠BOC>∠A,
∴∠A≠90°,故此种情形不存在;
②若∠B=90°,如答图2所示:
∵∠BOC=60°,∴∠BPO=30°,∴OP=2OB=2,又OP=2t,∴t=1;
③若∠APB=90°,如答图3所示:过点P作PD⊥AB于点D,
则OD=OP?cos30°=t,PD=OP?sin60°= t,
∴AD=OA+OD=2+t,BD=OB﹣OD=1﹣t.
在Rt△ABP中,由勾股定理得:PA2+PB2=AB2
∴(AD2+PD2)+(BD2+PD2)=AB2,
即[(2+t)2+( t)2]+[(1﹣t)2+( t)2]=32
解方程得:t= ,或t= (负值舍去),∴t= ,
综上所述,当△ABP是直角三角形时,t=1或t= 第38课时 几何动态综合题【答案】
(3)证明:如答图4,过点O作OE∥AP,交PB于点E,
则有 ,∴PE= PB.
∵AP=AB, ∴∠APB=∠B,
∵OE∥AP,
∴∠OEB=∠APB,
∴∠OEB=∠B,
∴OE=OB=1,∠3+∠B=180°.
∵AQ∥PB, ∴∠OAQ+∠B=180°, ∴∠OAQ=∠3;
∵∠AOP=∠1+∠QOP=∠2+∠B,∠QOP=∠B,
∴∠1=∠2; ∴△OAQ∽△PBO,
∴ ,即
化简得:AQ?PB=3.第38课时 几何动态综合题真题演练?层层推进
1.(2014广州)将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图2-①,测得AC=2,当∠B=60°时,如图2-②,AC=( ).
(A) (B)2 (C) (D) 图2-① 图2-② A第38课时 几何动态综合题2.(2014广东)如题25-1图,在△ABC中,AB=AC,AD⊥AB点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0)。
(1)当t=2时,连接DE、DF,求证:四边形AEDF为菱形;
(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;
(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值,若不存在,请说明理由。第38课时 几何动态综合题【答案】
(1)如图(1),连接DE,DF,
∵AB=AC,AD⊥BC, ∴BD=DC,
∵EF∥BC, ∴EF⊥AD,EH=FH,
∵t=2, ∴DH=4,
又AD=8,则AH=DH=4,
∴四边形AEDF是菱形;
(2)显然,BP=3t,DH=2t,则AH=8-2t,
∵EF∥BC, ∴ ,即 ,
∴EF= ,
设△PEF的面积为y,则
,即 ,
∴当t=2时,y有最大值为10,此时BP=6.第38课时 几何动态综合题【答案】
(3)存在满足条件的 ,理由如下:
如果△PEF是直角三角形,应分三种情况讨论:
① 当∠PEF=90°时,如图-1,则PE∥AD
所以 ,
此时,PE=DH=2t,BP=3t,
所以 ,解得t=0(舍去);
② 当∠EPF=90°时,如图-2,连接HP
则HP= EF= ,PD=│5-3t│
由勾股定理得,
解得 或t=0(舍去)
③ 当∠EFP=90°时,如图-3,则FP∥AD,
所以 ,即 ,解得 ,
综上所述,当 或 时,△PEF是直角三角形.第38课时 几何动态综合题3.(2013广东)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中, ∠FDE=90°,DF=4,DE= .将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,
则∠EMC=______度;
(2)如题25图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围.第38课时 几何动态综合题【答案】
(1)15;
(2)在Rt△CFA中,AC=6,∠ACF=∠E=30°,
∴FC= =6÷ ;(3)如图(4),设过点M作MN⊥AB于点N,则MN∥DE,∠NMB=∠B=45°,
∴NB=NM,NF=NB-FB=MN-x,∵MN∥DE,∴△FMN∽△FED,
∴ ,即 , ∴ ;
①当0≤x≤2时,如图(4) ,设DE与BC相交于点G ,则DG=DB=4+x,
∴ ,
即 ;第38课时 几何动态综合题【答案】
(3)②当 时,如图(5),
,
即 ;
③当 时, 如图(6) 设AC与EF交于点H,
∵AF=6-x,∠AHF=∠E=30°,∴AH= ,
;
综上所述,当 0≤x≤2 时, ,
当 时, ,
当 时, .第38课时 几何动态综合题课时作业一、选择题
1.如图,已知矩形ABCD的长AB为5,宽BC为4.E是BC边上的一个动点,AE⊥EF,EF交CD于点F.设BE=x,FC=y,则点 E从点B运动到点C时,能表示y关于x的函数关系的大致图象是( )
2.如图,一根长为5米的竹竿AB斜立于墙AC的右侧,底端B与墙角C的距离为3米,当竹竿顶端A下滑x米时,底端B便随着向右滑行y米,反映y与x变化关系 的大致图象是( )AA第38课时 几何动态综合题课时作业3.如图,将Rt△ABC绕点A按顺时针旋转一定角度得到Rt△ADE,点B的对应点D恰好落在BC边上.若AC= ,∠B=60°,则CD的长为( )
A.0.4 B.1.5 C. D.14.如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )
A.(2,10) B.(-2,0)
C.(2,10)或(-2,0) D.(10,2)或(-2,0)5.如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C,连结AA′,若∠1=20°,
则∠B的度数是( )
A.70° B.65° C.60° D.55°DCB第38课时 几何动态综合题课时作业二、填空题
6.如图,在△ABC中,AB=2,AC=4,将△ABC绕点C按逆 时针方向旋转得到△A′B′C,使CB′∥AB,分别延长AB,CA′相交于点D,则线段B D的长为 .7.在如图所示的平面直角坐标系中,点P是直线y=x上的动点,A(1,0),B(2,0)是x轴上的两点,则PA+PB的最小值为 .8.如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角. 当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,……第n次碰到矩形的边时的点为Pn. 则点P3的坐标是 ,点P2014的坐标是 .6(8,3)(5,0)第38课时 几何动态综合题课时作业9.如图,AB、CD是⊙O两条弦,AB=8,CD=6,MN是直径,AB⊥MN于E,CD⊥MN于点F,P为EF上任意一点,,则PA+PC的最小值为 .10.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD的中点,N是AB边上一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .第38课时 几何动态综合题课时作业三、解答题
11.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)求∠ACE的度数;
(3)求证:四边形ABEF是菱形.【答案】
(1)证明:∵ABC绕点A按逆时针方向旋转100°,
∴∠BAC=∠DAE=40°,
∴∠BAD=∠CAE=100°,
又∵AB=AC,
∴AB=AC=AD=AE,
∴△ABD≌△ACE(SAS).第38课时 几何动态综合题课时作业【答案】
(2)解:∵∠CAE=100°,AC=AE,
∴∠ACE= ,
(3)证明:∵∠BAD=∠CAE=140°,AB=AC=AD=AE,
∴∠ABD=∠ADB=∠ACE=∠AEC=20°.
∵∠BAE=∠BAD+∠DAE=160°,
∴∠BFE=360°﹣∠DAE﹣∠ABD﹣∠AEC=160°,
∴∠BAE=∠BFE,
∴四边形ABEF是平行四边形,
∵AB=AE,
∴平行四边形ABEF是菱形.第38课时 几何动态综合题课时作业12.如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG.
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的 与线段CG所围成的阴影部分的面积.第38课时 几何动态综合题课时作业【答案】
(1)证明:在正方形ABCD中,AB=BC=AD=2,∠ABC=90°,
∵△BEC绕点B逆时针旋转90°得到△ABF,
∴△ABF≌△CBE,
∴∠FAB=∠ECB,∠ABF=∠CBE=90°,AF=EC,
∴∠AFB+∠FAB=90°,
∵线段AF绕点F顺时针旋转90°得线段FG,
∴∠AFB+∠CFG=∠AFG=90°,
∴∠CFG=∠FAB=∠ECB,
∴EC∥FG,
∵AF=EC,AF=FG,
∴EC=FG,
∴四边形EFGC是平行四边形,
∴EF∥CG;第38课时 几何动态综合题课时作业【答案】
(2)解:∵AD=2,E是AB的中点,
∴FE=BE= AB=1,
∴AF= ,
由平行四边形的性质,知△FEC≌△CGF,
∴S△FEC =S△CGF,
∴S阴影=S扇形BAC+S△ABF+S△FGC-S扇形FAG
=
= .第38课时 几何动态综合题课时作业13.如图,已知正方形ABCD,把边DC绕D点顺时针旋转30°到DC′处,连接AC′ ,BC′,CC′,写出图中所有的等腰三角形,并写出推理过程.解:图中的所有的等腰三角形有:△DCC′,△DC′A,△C′AB,△C′BC,
理由如下:
∵四边形ABCD是正方形,
∴CD=AD=AB=BC,∠ADC=∠DAB=∠ABC=BCD=90°
由旋转的性质,知DC′=DC=AD=AB,∠DCC′=∠DC′C=75°,
∴△DC′C是等腰三角形
∵∠ADC =90°,∠CDC′=30°. ∴∠ADC′=60°
∵DC′=AD, ∴△DAC′为等边三角形
∴AC′=AD=AB,∠DAC′=∠DC′A=60°,
∴△ABC′为等腰三角形,∠BAC′=90°-60°=30°
∴∠ABC′=∠AC′B= (180°-30°)=75°
∴∠CBC′=90°-75°=15°,∠C′CB=90°-75°=15°
∴∠CBC′=∠C′CB. ∴△BCC′是等腰三角形.第38课时 几何动态综合题课时作业14.如图,在Rt△ABC中,∠B=90°,AC=60,AB=30.D是AC上的动点,过D作DF⊥BC于F,过F作FE∥AC,交AB于E.设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△DEF是直角三角形时,求x的值.【答案】
解:(1)∵在Rt△ABC中,∠B=90°,AC=60,AB=30,
∴∠C=30°,
∵CD=x,DF=y. ∴y= x ;
(2)∵四边形AEFD为菱形,
∴AD=DF, ∴y=60-x
解方程组 ,得x=40,y=20
∴当x=40时,四边形AEFD为菱形;第38课时 几何动态综合题课时作业【答案】
解:(3)∵△DEF是直角三角形,
∴∠FDE=90°,
∵FE∥AC,
∴∠EFB=∠C=30°,
∵DF⊥BC,
∴∠DEF+∠DFE=∠EFB+∠DFE,
∴∠DEF=∠EFB=30°,
∴EF=2DF,
∴60-x=2y ,
解方程组 ,得x=30 ,y=15.
∴当△DEF是直角三角形时,x=30.结束谢谢!
同课章节目录
