广东省2015中考数学冲刺复习课件:第37课时 与圆有关的综合题(共23张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第37课时 与圆有关的综合题(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 616.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:02:14 | ||
图片预览








文档简介
课件23张PPT。数学
第37课时 与圆有关的综合题第37课时 与圆有关的综合题知识考点?对应精练
【知识考点】
(1)圆与三角函数;
(2)圆与函数;
(3)圆与点、线、三角形;
(4)圆与多边形.【对应精练】
1.如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.
(1)求证:PB与⊙O相切;
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若AC=12,tan∠F= ,求cos∠ACB的值第37课时 与圆有关的综合题【解析】
(1)PA为⊙O的切线,
(2)AB⊥OP,由垂径定理,可得AD=BD,从而有PA=PB;
(3)证OB⊥PB即可说明PB为⊙O的切线,由△AOP≌△OPB,即有;
(4)由△OAD∽△OPA得OA2=OD?OP,由EF=2OA,代入可求EF,OD,OP之间关系;
(5)连接BE,构建Rt△BEF,由,tan∠F= ,可设BE=x,BF=2x,由勾股定理可得EF= ,由面积法求得BD= ,则AB= ,由勾股定理求得BC=20,则cos∠ACB可求.第37课时 与圆有关的综合题【答案】
(1)如图,连接OA,
∵PA与⊙O相切,∴PA⊥OA,即∠OAP=90°,
∵OP⊥AB,
∴D为AB的中点,即OP垂直平分AB,∴PA=PB,
又OA=OB,OP=OP,
∴△OAP≌△OBP(SSS),∴∠OAP=∠OBP=90°,
∴BP⊥OB,即PB与⊙O相切;
(2)EF2=4OD?OP,理由如下:
∵∠OAP=∠ADO=90°,∠AOD=∠POA,
∴△OAD∽△OPA,
∴ ,即OA2=OD?OP,
∵EF=2OA, ∴ EF2=OD?OP,即EF2=4OD?OP;第37课时 与圆有关的综合题【答案】
(3)如图,连接BE,则∠FBE=90°,
∵ , ∴ ,
设BE=x,则BF=2x,
∴EF= ,
∵ BE?BF= EF?BD,
∴BD= ,
∴AB=2BD= ,
∵AC2+AB2=BC2,即
∴ ,
∴BC= ,
∴ .第37课时 与圆有关的综合题【方法总结】
(1)看到求圆的切线,想到:有交点,连半径,证垂直;无交点,作垂直,证半径;
(2)看到圆中的三角函数,想到三角函数一般在直角三角形中使用,直径所对的圆周角是直角;
(3)看到过圆外的同一点的两条切线,想到切线长定理;
(4)看到垂直于弦的直径,想到垂径定理.
【失分盲点】
(1)易忽视圆中的两条半径构成等腰三角形这个条件;
(2)在证明一条直线是圆的切线时,若直线与圆的公共点未确定时,易犯证明直线与半径垂直的错误;
(3)在圆中的三角形,易犯不说明其为直角三角形就应用三角函数解决问题的错误.第37课时 与圆有关的综合题真题演练?层层推进
1.(2014广东梅州)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB= ,求⊙O的面积.【答案】
(1)证明:如图,连接OC,
∵在△ABO中,OA=OB,C是边AB的中点,∴OC⊥AB,
∵以O为圆心的圆过点C,∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°, ∴∠A=∠B=30°,
∵AB= ,C是边AB的中点,
∴AC= AB= , ∴OC=AC?tan∠A= =2,
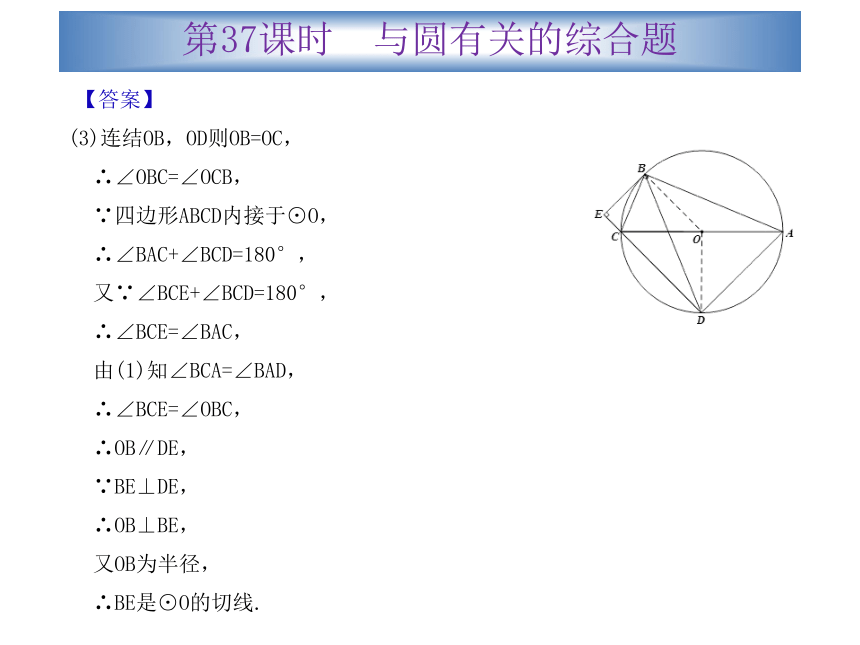
∴⊙O的面积为:π×22=4π.第37课时 与圆有关的综合题2.(2013广东)如题24图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.【答案】
(1)∵AB=DB,
∴∠BDA=∠BAD,
又∵∠BDA=∠BCA,
∴∠BCA=∠BAD.
(2)在Rt△ABC中,AC= ,
易证△ACB∽△DBE,得 ,
∴DE= 第37课时 与圆有关的综合题【答案】
(3)连结OB,OD则OB=OC,
∴∠OBC=∠OCB,
∵四边形ABCD内接于⊙O,
∴∠BAC+∠BCD=180°,
又∵∠BCE+∠BCD=180°,
∴∠BCE=∠BAC,
由(1)知∠BCA=∠BAD,
∴∠BCE=∠OBC,
∴OB∥DE,
∵BE⊥DE,
∴OB⊥BE,
又OB为半径,
∴BE是⊙O的切线.第37课时 与圆有关的综合题3.(2014广东)如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)PF是⊙O的切线。
【答案】
(1)因为OC= AC=6,∠POC=60°,
所以劣弧PC的长为 =2π;
(2)因为OD⊥AB,PE⊥AC
所以∠ODA=∠OEP=90°,
又因为∠AOD=∠POE,OA=OP,
所以△OAD≌△OPE(AAS)
所以OD=OE;第37课时 与圆有关的综合题【答案】
(3)如图,连接AP,
∵OD=OE,OA=OP
∴∠1=∠2= ∠POC,
∵PD⊥AB,AC为⊙O的直径
∴∠PDA=∠FBD=90 °,
∴PD∥FB ∴∠1=∠3 ∴∠2=∠3
∵OD⊥AB ∴AD=BD
∴△ADP≌△DBF(AAS) ∴DP=FB
∴四边形DBFP是矩形
∴∠DPF=90 °,即OP⊥PF
又∵OP为⊙O的半径
∴PF是⊙O的切线.第37课时 与圆有关的综合题课时作业一、选择题
1.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.160° B.150° C.140° D.120°2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.33.如图,AB是⊙O的弦,AC切⊙O于点A,BC经过圆心.若∠B=25°,则∠C的度数为( )
A.20° B.25° C.40° D.50°4.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿 轴正方向平移,使⊙P与 轴相切,则平移的距离为( )
A. 1 B. 1或5 C. 5 D. 1或6BCCB第37课时 与圆有关的综合题课时作业二、填空题
6.如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .5.如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC 上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC= ;③sin∠AOB= ; ④四边形ABOC是菱形.
其中正确结论的序号是( )
A.①③ B.①②③④ C.②③④ D①③④7.如图,在△ABC中∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为 .8.已知⊙O的面积为2π,则其内接正三角形的面积为 .B350°第37课时 与圆有关的综合题课时作业三、解答题
11.如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD= ,求⊙O的半径.9.如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E= .10.一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 cm.3第37课时 与圆有关的综合题课时作业【答案】
(1)证:如图,连结OC,
∵ ,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
又OC为半径,
∴CD是⊙O的切线;第37课时 与圆有关的综合题课时作业【答案】
(2)解:如图,连结BC,
∵AB为直径,
∴∠ACB=90°,
∵ ,
∴∠BOC= ×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD= ,
∴AC=2CD= ,
在Rt△ACB中,BC= AC=4,
∴AB=2BC=4,
∴⊙O的半径为4.第37课时 与圆有关的综合题课时作业12.如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.【答案】
(1)证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵AB、BC、CD分别与⊙O相切于E、F、G,
∴BO平分∠ABC,CO平分∠DCB,
∴∠OBC= ∠ABC,∠OCB= ∠DCB,
∴∠OBC+∠OCB= (∠ABC+∠DCB)=90°,
∴∠BOC=90°,
∴BO⊥CO.第37课时 与圆有关的综合题课时作业【答案】
(2)解:连接OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO,
∴ ,
∵在Rt△BOF中,
BO=6cm,CO=8cm,
∴BC= =10cm,
∴ ,
∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,
∴BE=BF=3.6cm,CG=CF,
∵CF=BC﹣BF=10-3.6=6.4cm.
∴CG=CF=6.4cm.第37课时 与圆有关的综合题课时作业13.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,线段AB为半圆O的直径,将Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交于点H.
(1)求BE的长;
(2)求Rt△ABC与△DEF重叠(阴影)部分的面积.【答案】
(1)如图,连结OG,
∵∠BAC=90°,AB=4,AC=3,∴BC= =5,
由平移的性质,可知:AD=BE,DF=AC=3,EF=BC=5,∠EDF=∠BAC=90°,
∵EF与半圆O相切于点G,∴OG⊥EF,
∵AB=4,线段AB为半圆O的直径,∴OB=OG=2,
∵∠GEO=∠DEF,∴Rt△EOG∽Rt△EFD,
∴ ,即 ,解得OE= ,
∴BE=OE-OB= ;第37课时 与圆有关的综合题课时作业14.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD?BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.第37课时 与圆有关的综合题课时作业【答案】
(1)如图,连接OD.
∵DE为切线,
∴∠EDC+∠ODC=90°;
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴ED=EC;
∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,
∴∠B=∠BDE,
∴ED=DB.∴EB=EC,即点E为边BC的中点;第37课时 与圆有关的综合题课时作业【答案】
(2)∵AC为直径,
∴∠ADC=∠ACB=90°,
又∵∠B=∠B
∴△ABC∽△CDB,
∴ ,
∴BC2=BD?BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;
∵AC为直径,
∴∠ADC=90°,
∴∠CAD=∠ADC-∠OCD=90°-45°=45°
∴Rt△ABC为等腰直角三角形.结束谢谢!
【知识考点】
(1)圆与三角函数;
(2)圆与函数;
(3)圆与点、线、三角形;
(4)圆与多边形.【对应精练】
1.如图,PA为⊙O的切线,A为切点,直线PO交⊙O与点E,F过点A作PO的垂线AB垂足为D,交⊙O与点B,延长BO与⊙O交与点C,连接AC,BF.
(1)求证:PB与⊙O相切;
(2)试探究线段EF,OD,OP之间的数量关系,并加以证明;
(3)若AC=12,tan∠F= ,求cos∠ACB的值第37课时 与圆有关的综合题【解析】
(1)PA为⊙O的切线,
(2)AB⊥OP,由垂径定理,可得AD=BD,从而有PA=PB;
(3)证OB⊥PB即可说明PB为⊙O的切线,由△AOP≌△OPB,即有;
(4)由△OAD∽△OPA得OA2=OD?OP,由EF=2OA,代入可求EF,OD,OP之间关系;
(5)连接BE,构建Rt△BEF,由,tan∠F= ,可设BE=x,BF=2x,由勾股定理可得EF= ,由面积法求得BD= ,则AB= ,由勾股定理求得BC=20,则cos∠ACB可求.第37课时 与圆有关的综合题【答案】
(1)如图,连接OA,
∵PA与⊙O相切,∴PA⊥OA,即∠OAP=90°,
∵OP⊥AB,
∴D为AB的中点,即OP垂直平分AB,∴PA=PB,
又OA=OB,OP=OP,
∴△OAP≌△OBP(SSS),∴∠OAP=∠OBP=90°,
∴BP⊥OB,即PB与⊙O相切;
(2)EF2=4OD?OP,理由如下:
∵∠OAP=∠ADO=90°,∠AOD=∠POA,
∴△OAD∽△OPA,
∴ ,即OA2=OD?OP,
∵EF=2OA, ∴ EF2=OD?OP,即EF2=4OD?OP;第37课时 与圆有关的综合题【答案】
(3)如图,连接BE,则∠FBE=90°,
∵ , ∴ ,
设BE=x,则BF=2x,
∴EF= ,
∵ BE?BF= EF?BD,
∴BD= ,
∴AB=2BD= ,
∵AC2+AB2=BC2,即
∴ ,
∴BC= ,
∴ .第37课时 与圆有关的综合题【方法总结】
(1)看到求圆的切线,想到:有交点,连半径,证垂直;无交点,作垂直,证半径;
(2)看到圆中的三角函数,想到三角函数一般在直角三角形中使用,直径所对的圆周角是直角;
(3)看到过圆外的同一点的两条切线,想到切线长定理;
(4)看到垂直于弦的直径,想到垂径定理.
【失分盲点】
(1)易忽视圆中的两条半径构成等腰三角形这个条件;
(2)在证明一条直线是圆的切线时,若直线与圆的公共点未确定时,易犯证明直线与半径垂直的错误;
(3)在圆中的三角形,易犯不说明其为直角三角形就应用三角函数解决问题的错误.第37课时 与圆有关的综合题真题演练?层层推进
1.(2014广东梅州)如图,在△ABO中,OA=OB,C是边AB的中点,以O为圆心的圆过点C.
(1)求证:AB与⊙O相切;
(2)若∠AOB=120°,AB= ,求⊙O的面积.【答案】
(1)证明:如图,连接OC,
∵在△ABO中,OA=OB,C是边AB的中点,∴OC⊥AB,
∵以O为圆心的圆过点C,∴AB与⊙O相切;
(2)解:∵OA=OB,∠AOB=120°, ∴∠A=∠B=30°,
∵AB= ,C是边AB的中点,
∴AC= AB= , ∴OC=AC?tan∠A= =2,
∴⊙O的面积为:π×22=4π.第37课时 与圆有关的综合题2.(2013广东)如题24图,⊙O是Rt△ABC的外接圆,∠ABC=90°,弦BD=BA,AB=12,BC=5,BE⊥DC交DC的延长线于点E.
(1)求证:∠BCA=∠BAD;
(2)求DE的长;
(3)求证:BE是⊙O的切线.【答案】
(1)∵AB=DB,
∴∠BDA=∠BAD,
又∵∠BDA=∠BCA,
∴∠BCA=∠BAD.
(2)在Rt△ABC中,AC= ,
易证△ACB∽△DBE,得 ,
∴DE= 第37课时 与圆有关的综合题【答案】
(3)连结OB,OD则OB=OC,
∴∠OBC=∠OCB,
∵四边形ABCD内接于⊙O,
∴∠BAC+∠BCD=180°,
又∵∠BCE+∠BCD=180°,
∴∠BCE=∠BAC,
由(1)知∠BCA=∠BAD,
∴∠BCE=∠OBC,
∴OB∥DE,
∵BE⊥DE,
∴OB⊥BE,
又OB为半径,
∴BE是⊙O的切线.第37课时 与圆有关的综合题3.(2014广东)如图,⊙O是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙O于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF.
(1)若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)求证:OD=OE;
(3)PF是⊙O的切线。
【答案】
(1)因为OC= AC=6,∠POC=60°,
所以劣弧PC的长为 =2π;
(2)因为OD⊥AB,PE⊥AC
所以∠ODA=∠OEP=90°,
又因为∠AOD=∠POE,OA=OP,
所以△OAD≌△OPE(AAS)
所以OD=OE;第37课时 与圆有关的综合题【答案】
(3)如图,连接AP,
∵OD=OE,OA=OP
∴∠1=∠2= ∠POC,
∵PD⊥AB,AC为⊙O的直径
∴∠PDA=∠FBD=90 °,
∴PD∥FB ∴∠1=∠3 ∴∠2=∠3
∵OD⊥AB ∴AD=BD
∴△ADP≌△DBF(AAS) ∴DP=FB
∴四边形DBFP是矩形
∴∠DPF=90 °,即OP⊥PF
又∵OP为⊙O的半径
∴PF是⊙O的切线.第37课时 与圆有关的综合题课时作业一、选择题
1.如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
A.160° B.150° C.140° D.120°2.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.33.如图,AB是⊙O的弦,AC切⊙O于点A,BC经过圆心.若∠B=25°,则∠C的度数为( )
A.20° B.25° C.40° D.50°4.如图,在平面直角坐标系中,半径为2的⊙P的圆心P的坐标为(﹣3,0),将⊙P沿 轴正方向平移,使⊙P与 轴相切,则平移的距离为( )
A. 1 B. 1或5 C. 5 D. 1或6BCCB第37课时 与圆有关的综合题课时作业二、填空题
6.如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .5.如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC 上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC= ;③sin∠AOB= ; ④四边形ABOC是菱形.
其中正确结论的序号是( )
A.①③ B.①②③④ C.②③④ D①③④7.如图,在△ABC中∠A=25°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E,则 的度数为 .8.已知⊙O的面积为2π,则其内接正三角形的面积为 .B350°第37课时 与圆有关的综合题课时作业三、解答题
11.如图,AB是⊙O的直径,点F,C是⊙O上两点,且 ,连接AC,AF,过点C作CD⊥AF交AF延长线于点D,垂足为D.
(1)求证:CD是⊙O的切线;
(2)若CD= ,求⊙O的半径.9.如图,直线MN与⊙O相切于点M,ME=EF且EF∥MN,则cos∠E= .10.一个边长为4cm的等边三角形ABC与⊙O等高,如图放置,⊙O与BC相切于点C,⊙O与AC相交于点E,则CE的长为 cm.3第37课时 与圆有关的综合题课时作业【答案】
(1)证:如图,连结OC,
∵ ,
∴∠FAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠FAC=∠OCA,
∴OC∥AF,
∵CD⊥AF,
∴OC⊥CD,
又OC为半径,
∴CD是⊙O的切线;第37课时 与圆有关的综合题课时作业【答案】
(2)解:如图,连结BC,
∵AB为直径,
∴∠ACB=90°,
∵ ,
∴∠BOC= ×180°=60°,
∴∠BAC=30°,
∴∠DAC=30°,
在Rt△ADC中,CD= ,
∴AC=2CD= ,
在Rt△ACB中,BC= AC=4,
∴AB=2BC=4,
∴⊙O的半径为4.第37课时 与圆有关的综合题课时作业12.如图,AB,BC,CD分别与⊙O相切于E,F,G.且AB∥CD.BO=6cm,CO=8cm.
(1)求证:BO⊥CO;
(2)求BE和CG的长.【答案】
(1)证明:∵AB∥CD
∴∠ABC+∠BCD=180°
∵AB、BC、CD分别与⊙O相切于E、F、G,
∴BO平分∠ABC,CO平分∠DCB,
∴∠OBC= ∠ABC,∠OCB= ∠DCB,
∴∠OBC+∠OCB= (∠ABC+∠DCB)=90°,
∴∠BOC=90°,
∴BO⊥CO.第37课时 与圆有关的综合题课时作业【答案】
(2)解:连接OF,则OF⊥BC,
∴Rt△BOF∽Rt△BCO,
∴ ,
∵在Rt△BOF中,
BO=6cm,CO=8cm,
∴BC= =10cm,
∴ ,
∴BF=3.6cm,
∵AB、BC、CD分别与⊙O相切,
∴BE=BF=3.6cm,CG=CF,
∵CF=BC﹣BF=10-3.6=6.4cm.
∴CG=CF=6.4cm.第37课时 与圆有关的综合题课时作业13.如图,在Rt△ABC中,∠BAC=90°,AB=4,AC=3,线段AB为半圆O的直径,将Rt△ABC沿射线AB方向平移,使斜边与半圆O相切于点G,得△DEF,DF与BC交于点H.
(1)求BE的长;
(2)求Rt△ABC与△DEF重叠(阴影)部分的面积.【答案】
(1)如图,连结OG,
∵∠BAC=90°,AB=4,AC=3,∴BC= =5,
由平移的性质,可知:AD=BE,DF=AC=3,EF=BC=5,∠EDF=∠BAC=90°,
∵EF与半圆O相切于点G,∴OG⊥EF,
∵AB=4,线段AB为半圆O的直径,∴OB=OG=2,
∵∠GEO=∠DEF,∴Rt△EOG∽Rt△EFD,
∴ ,即 ,解得OE= ,
∴BE=OE-OB= ;第37课时 与圆有关的综合题课时作业14.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证:BC2=BD?BA;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.第37课时 与圆有关的综合题课时作业【答案】
(1)如图,连接OD.
∵DE为切线,
∴∠EDC+∠ODC=90°;
∵∠ACB=90°,
∴∠ECD+∠OCD=90°.
又∵OD=OC,
∴∠ODC=∠OCD,
∴∠EDC=∠ECD,
∴ED=EC;
∵AC为直径,∴∠ADC=90°,
∴∠BDE+∠EDC=90°,∠B+∠ECD=90°,
∴∠B=∠BDE,
∴ED=DB.∴EB=EC,即点E为边BC的中点;第37课时 与圆有关的综合题课时作业【答案】
(2)∵AC为直径,
∴∠ADC=∠ACB=90°,
又∵∠B=∠B
∴△ABC∽△CDB,
∴ ,
∴BC2=BD?BA;
(3)当四边形ODEC为正方形时,∠OCD=45°;
∵AC为直径,
∴∠ADC=90°,
∴∠CAD=∠ADC-∠OCD=90°-45°=45°
∴Rt△ABC为等腰直角三角形.结束谢谢!
同课章节目录
