广东省2015中考数学冲刺复习课件:第36课时 二次函数综合题(共33张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第36课时 二次函数综合题(共33张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 619.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:03:00 | ||
图片预览










文档简介
课件33张PPT。数学
第36课时 二次函数综合题第36课时 二次函数综合题知识考点?对应精练
【知识考点】
(1)二次函数的最值问题;
(2)二次函数的存在性问题;
(3)二次函数的平移;
(4)二次函数和圆.【对应精练】
1.如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(-1,0),以AB的中点P为圆心,AB为直径作⊙P交y轴的正半轴于点C.
(1)求经过A、B、C三点的抛物线的解析式;
(2)设M为(1)中抛物线的顶点,求直线MC的解析式;
(3)试说明直线MC与P的位置关系,并证明你的结论.第36课时 二次函数综合题【解析】
(1)点A(4,0)和B(-1,0)都在x轴上,且OA=4,OB=1;
(2)以AB的中点P为圆心,AB为直径作⊙P交y轴的正半轴于点C,即△ABC是直角三角形,由相似三角形可得OC2=OA×OB,即可求OC和点C的坐标;
(3)可设交点式y=a(x+1)(x-4),将点C坐标,代入求a即可;
(4)点M是抛物线顶点坐标,将M和C的坐标代入直线y=kx+b即可求直线MC的解析式;
(5)连接CP,判断CP是垂直MC,需要由勾股定理逆定理,判断△CDP是否为直角三角形即可.第36课时 二次函数综合题【答案】
(1)∵A(4,0) ,B(-1,0)
∴AB=5,且PC=PB=PA=
∴OP= ,即P
在Rt△CPO中,OC= ,即C点的坐标为(0,2),
设抛物线的解析式为y=a(x+1)(x-4),则
-4a=2,即a=
∴抛物线的解析式为- (x+1)(x-4),即y=- x2+ x+2 .
(2)由 ,得
∴顶点坐标M为
设直线MC的解析式为y=kx+b,则 ,
解得k= ,b=2 ,
∴直线MC的解析式为 x+2;第36课时 二次函数综合题【答案】
(3)MC与⊙P相切,理由如下:
设直线MC与x轴交于点D,则D
∵ ,
, ,
∴CD2+PC2=PD2
∴∠PCD=90,即PC⊥DC ,
又PC为半径
∴MC是⊙P的切线第36课时 二次函数综合题【方法总结】
(1)看到点坐标,想到点坐标的位置或点到坐标轴的距离或两点之间距离;
(2)看到求二次函数的解析式,想到寻找三个条件(点坐标)或对称轴或抛物线与x轴的交点,相应地有一般式、顶点式、交点式;
(3)看到求抛物线的顶点或最值问题,想到配方法转化抛物线为顶点式;
(4)抛物线的平移规律:上加下减,左加右减;
(5)解题思考方向:点坐标→线段长度→面积→条件;条件→线段长度→点坐标;
【失点盲点】
(1)在解决二次函数有关单调性,最值问题时,忽略二次项系数;
(2)在解决与二次函数有关的实际问题时,一是不能建立正确的函数关系缺乏建模思想;二是对自变量取值范围的忽略;
(3)对于二次函数的最值问题,误认为自变量取对称轴与 的交点时,函数值有最值.第36课时 二次函数综合题真题演练?层层推进
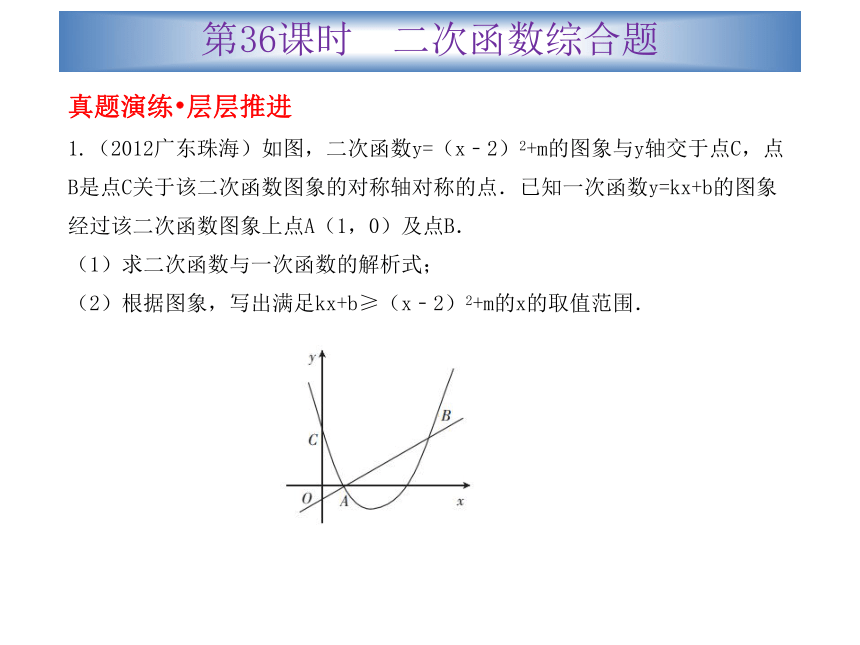
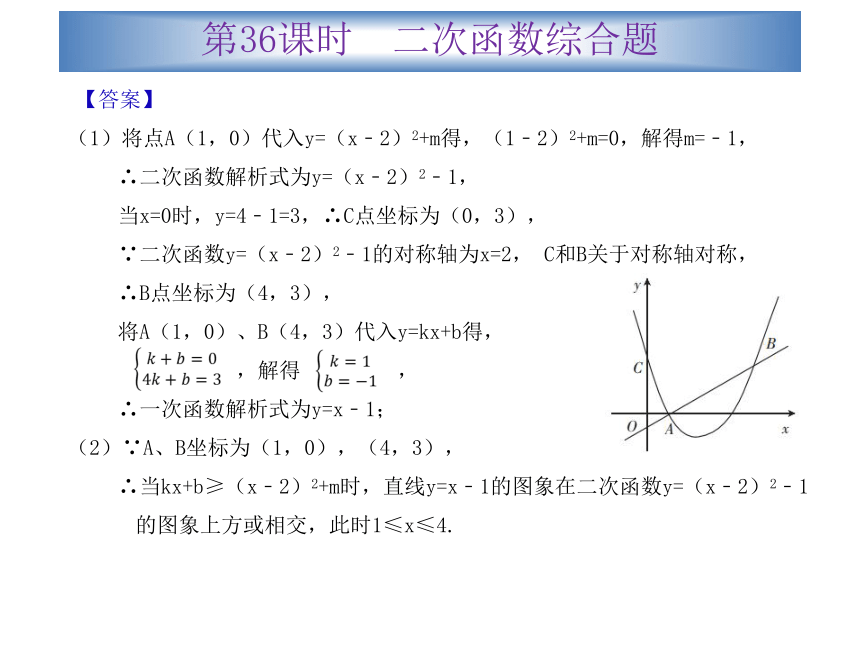
1.(2012广东珠海)如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.第36课时 二次函数综合题【答案】
(1)将点A(1,0)代入y=(x﹣2)2+m得,(1﹣2)2+m=0,解得m=﹣1,
∴二次函数解析式为y=(x﹣2)2﹣1,
当x=0时,y=4﹣1=3,∴C点坐标为(0,3),
∵二次函数y=(x﹣2)2﹣1的对称轴为x=2, C和B关于对称轴对称,
∴B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得,
,解得 ,
∴一次函数解析式为y=x﹣1;
(2)∵A、B坐标为(1,0),(4,3),
∴当kx+b≥(x﹣2)2+m时,直线y=x﹣1的图象在二次函数y=(x﹣2)2﹣1的图象上方或相交,此时1≤x≤4.
第36课时 二次函数综合题2.(2012广东)如图,抛物线y= x2- x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).第36课时 二次函数综合题【答案】
(1)在y= x2- x-9中,
令x=0,得y=-9,∴C(0,﹣9);
令y=0,即 x2- x-9 ,解得:x1=﹣3,x2=6,
∴A(﹣3,0)、B(6,0),∴AB=9,OC=9。
(2)∵ED∥BC,∴△AED∽△ABC,∴ ,即: ,
∴s= m2(0<m<9)。第36课时 二次函数综合题【答案】
(3)∵S△AEC= AE?OC= m,S△AED =s= m2,
∴S△EDC=S△AEC﹣S△AED= 。
∴△CDE的最大面积为 ,
此时,AE=m= ,BE=AB﹣AE= 。
又 ,
过E作EF⊥BC于F,则Rt△BEF∽Rt△BCO,得: ,
即: 。
∴ 。
∴以E点为圆心,与BC相切的圆的面积 S⊙E=π?EF2= 。第36课时 二次函数综合题3.(2012广州)如图,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.【答案】
(1)在 中,令y=0,即 ,
解得x1=﹣4,x2=2。
∵点A在点B的左侧,
∴A、B点的坐标为A(﹣4,0)、B(2,0);第36课时 二次函数综合题【答案】
(2)由 得,对称轴为x=-1.
在 中,令x=0,得y=3.
∴OC=3,AB=6, .
在Rt△AOC中,
设△ACD中AC边上的高为h,则有 AC?h=9,解得h= 。
如图1,在坐标平面内作直线平行于AC,且到AC的距离=h= ,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D
设L1交y轴于E,过C作CF⊥L1于F,则CF=h= ,
∴ 。第36课时 二次函数综合题【答案】
(2)(接上页)
设直线AC的解析式为y=kx+b,
将A(﹣4,0),B(0,3)坐标代入,得
,解得 。
∴直线AC解析式为y= x+3。
直线L1可以看做直线AC向下平移CE长度单位( 个长度单位)而形成的,
∴直线L1的解析式为 ,
则D1的纵坐标为 。∴D1(﹣4, ),
同理,直线AC向上平移 个长度单位得到L2,可求得D2(﹣1, ),
综上所述,D点坐标为:D1(﹣4, ),D2(﹣1, );第36课时 二次函数综合题【答案】(3)如图2,以AB为直径作⊙F,圆心为F.
过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N,
∵A(﹣4,0),B(2,0),∴F(﹣1,0),
⊙F半径FM=FB=3,又FE=5,
则在Rt△MEF中,ME= ,sin∠MFE= ,cos∠MFE= ,
在Rt△FMN中,MN=MN?sin∠MFE=3× = ,
FN=MN?cos∠MFE=3× = ,
则ON= 。∴M点坐标为( , ),
直线l过M( , ),E(4,0),
设直线l的解析式为y=k1x+b1,则有 ,解得 ,
∴直线l的解析式为y= x+3,
同理,可以求得另一条切线的解析式为y= x﹣3,
综上所述,直线l的解析式为y= x+3或y= x﹣3.第36课时 二次函数综合题4.(2014深圳)如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.第36课时 二次函数综合题【答案】
(1)直线AB的解析式为y=2x+4,
令x=0,得y=4;令y=0,得x=﹣2.
∴A(﹣2,0)、B(0,4).
∵抛物线的顶点为点A(﹣2,0),
∴设抛物线的解析式为:y=a(x+2)2,
点C(0,﹣4)在抛物线上,代入上式得:﹣4=4a,解得a=﹣1,
∴抛物线的解析式为y=﹣(x+2)2.第36课时 二次函数综合题【答案】
(2)平移过程中,设点E的坐标为(m,2m+4),
则平移后抛物线的解析式为:y=﹣(x﹣m)2+2m+4,
∴F(0,﹣m2+2m+4).
①∵点E为顶点,∴∠BEF≥90°,
∴若△BEF与△BAO相似,只能是点E作为直角顶点,
∴△BAO∽△BFE,
∴ ,即 ,可得:BE=2EF.
如答图2﹣1,过点E作EH⊥y轴于点H,则点H坐标为:H(0,2m+4).
∵B(0,4),H(0,2m+4),F(0,﹣m2+2m+4),
∴BH=|2m|,FH=|﹣m2|.
在Rt△BEF中,由相似三角形性质得:BE2=BH?BF,EF2=FH?BF,第36课时 二次函数综合题【答案】
(2)又∵BE=2EF,∴BH=4FH,
即:4|﹣m2|=|2m|.
若﹣4m2=2m,解得m=- 或m=0(与点B重合,舍去);
若﹣4m2=﹣2m,解得m= 或m=0(与点B重合,舍去),此时点E位于第一象限,∠BEF为钝角,故此情形不成立.
∴m=- ,∴E(- ,3).
②假设存在.联立抛物线:y=﹣(x+2)2与直线AB:y=2x+4,
可求得:D(﹣4,﹣4),∴S△ACD= ×4×4=8,
∵S△EFG与S△ACD存在8倍的关系,∴S△EFG=64或S△EFG=1.
联立平移抛物线:y=﹣(x﹣m)2+2m+4与直线AB:y=2x+4,
可求得:G(m﹣2,2m).
∴点E与点M横坐标相差2,即: .第36课时 二次函数综合题【答案】
(2)如答图2﹣2,S△EFG =S△BFG ﹣S△BEF
= BF? ﹣ BF = BF?( )=BF.
∵B(0,4),F(0,﹣m2+2m+4),∴BF=|﹣m2+2m|.
∴|﹣m2+2m|=64或|﹣m2+2m|=1,
∴﹣m2+2m可取值为:64、﹣64、1、﹣1.
当取值为64时,一元二次方程﹣m2+2m=64无解,故﹣m2+2m≠64.
∴﹣m2+2m可取值为:﹣64、1、﹣1.
∵F(0,﹣m2+2m+4),
∴F坐标为:(0,﹣60)、(0,3)、(0,5).
综上所述,S△EFG与S△ACD存在8倍的关系,点F坐标为(0,﹣60)、(0,3)、(0,5).第36课时 二次函数综合题课时作业一、选择题
1.抛物线y=2x2,y=-2x2,y= x2共有的性质是( )
A.开口向下 B.对称轴是y轴 C.都有最低点 D. 随x的增大而减小2.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=-1
C.顶点坐标中(1,2) D.与x轴有两个交点3.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.对称轴是x=
C.当x< 时, 随x的增大而减小
D.当-10 BCD第36课时 二次函数综合题课时作业4.已知二次函数y=ax2+bx+c(a≠0)的图象如图,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,有下列结论:①b2﹣4ac>0;②abc<0;③m>2.
其中,正确结论的个数是( )
A.0 B.1 C.2 D.35.已知a、h、k为三数,且二次函数y=a(x-h)2+k在坐标平面上的图形通过(0,5)、(10,8)两点.若a<0,0<h<10,则h之值可能为下列何者?( )
A.1 B.3 C.5 D.7DD第36课时 二次函数综合题课时作业二、填空题
6.抛物线y=x2-2x+3的顶点坐标是 .7.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当y<5时,x的取值范围是 .8.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 .9.如图,抛物线y=ax2+bx+c的对称轴x=1,若点P(4,0)在该抛物线上,则4a-2b+c的值为 .(1,2)0<x<4x=20第36课时 二次函数综合题课时作业10.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:
若m,n(m A. m11.如图,已知二次函数 的图象经过原点O(0,0),A(2,0).
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,
试判断点A′是否为该函数图象的顶点?第36课时 二次函数综合题课时作业【答案】
(1)抛物线的对称轴为x=1;
(2)点A′是该函数图象的顶点.理由如下:
由(1)可知,抛物线 的顶点坐标为(1, ),
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=2,
在Rt△A′OB中,∠OA′B=30°,
∴OB= OA′=1,
∴A′B= OB= ,
∴A′点的坐标为(1, ),
∴点A′为抛物线 的顶点.第36课时 二次函数综合题课时作业12.二次函数图象的顶点在原点O,经过点A ;点F(0,1)在y轴上.直线 y=-1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.第36课时 二次函数综合题课时作业【答案】
(1)解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1, )代入y=ax2得,a= ,
∴二次函数的解析式为y= x2;
(2)证明:∵点P在抛物线y= x2上,
∴可设点P的坐标为(x, x2) ,
如图,过点P作PB⊥y轴于点B,则BF= x2-1,PB=x,
∴Rt△BPF中,PF= = x2+1,
∴PM= x2+1,
∴PF=PM,∴∠PFM=∠PMF,
又∵PM∥x轴,∴∠MFH=∠PMF,∴∠PFM=∠MFH,
∴FM平分∠OFP;第36课时 二次函数综合题课时作业【答案】
(3)解:当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴ x2+1=4,
解得:x=±2 ,
∴ x2= ×12=3 ,
∴满足条件的点P的坐标为(-2 ,3) 或(2 ,3).第36课时 二次函数综合题课时作业13.如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNE的面积之比.【答案】
(1)将A(-1,0)代入y=-x2+2x+c,得c=3,
∴抛物线的解析式为y=-x2+2x+3,
∵ y=-x2+2x+3=-(x-1)2+4
∴抛物线的顶点坐标为(1,4);
(2)∵A(-1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),∴EM=1,BN=2,
∵EM∥BN, ∴△EMF∽△BNF,
∴ 第36课时 二次函数综合题课时作业14.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x<50)天的售价与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
第36课时 二次函数综合题课时作业【答案】
(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x=200
当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000;
(2)当1≤x<50时,将二次函数配方:y=-2x2+180x+200=-2(x-45)2+6050
∴当x=45时,y有最大值,最大值为6050;
当50≤x≤90时,函数y=-120x+12000是一次函数,y随x的增大而减小,
当x=50时,y有最大值,y最大值为6000;
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)当y=4800时,对于-2(x-45)2+6050=4800,有x=20或x=60
∴当20≤x≤50时,y≥4800;
当y=4800时,对于120x+12000≥4800,有x≤60;
综上所述,当20≤x≤60时,每天销售利润不低于4800元.
结束谢谢!
【知识考点】
(1)二次函数的最值问题;
(2)二次函数的存在性问题;
(3)二次函数的平移;
(4)二次函数和圆.【对应精练】
1.如图,在平面直角坐标系中,坐标原点为O,A点坐标为(4,0),B点坐标为(-1,0),以AB的中点P为圆心,AB为直径作⊙P交y轴的正半轴于点C.
(1)求经过A、B、C三点的抛物线的解析式;
(2)设M为(1)中抛物线的顶点,求直线MC的解析式;
(3)试说明直线MC与P的位置关系,并证明你的结论.第36课时 二次函数综合题【解析】
(1)点A(4,0)和B(-1,0)都在x轴上,且OA=4,OB=1;
(2)以AB的中点P为圆心,AB为直径作⊙P交y轴的正半轴于点C,即△ABC是直角三角形,由相似三角形可得OC2=OA×OB,即可求OC和点C的坐标;
(3)可设交点式y=a(x+1)(x-4),将点C坐标,代入求a即可;
(4)点M是抛物线顶点坐标,将M和C的坐标代入直线y=kx+b即可求直线MC的解析式;
(5)连接CP,判断CP是垂直MC,需要由勾股定理逆定理,判断△CDP是否为直角三角形即可.第36课时 二次函数综合题【答案】
(1)∵A(4,0) ,B(-1,0)
∴AB=5,且PC=PB=PA=
∴OP= ,即P
在Rt△CPO中,OC= ,即C点的坐标为(0,2),
设抛物线的解析式为y=a(x+1)(x-4),则
-4a=2,即a=
∴抛物线的解析式为- (x+1)(x-4),即y=- x2+ x+2 .
(2)由 ,得
∴顶点坐标M为
设直线MC的解析式为y=kx+b,则 ,
解得k= ,b=2 ,
∴直线MC的解析式为 x+2;第36课时 二次函数综合题【答案】
(3)MC与⊙P相切,理由如下:
设直线MC与x轴交于点D,则D
∵ ,
, ,
∴CD2+PC2=PD2
∴∠PCD=90,即PC⊥DC ,
又PC为半径
∴MC是⊙P的切线第36课时 二次函数综合题【方法总结】
(1)看到点坐标,想到点坐标的位置或点到坐标轴的距离或两点之间距离;
(2)看到求二次函数的解析式,想到寻找三个条件(点坐标)或对称轴或抛物线与x轴的交点,相应地有一般式、顶点式、交点式;
(3)看到求抛物线的顶点或最值问题,想到配方法转化抛物线为顶点式;
(4)抛物线的平移规律:上加下减,左加右减;
(5)解题思考方向:点坐标→线段长度→面积→条件;条件→线段长度→点坐标;
【失点盲点】
(1)在解决二次函数有关单调性,最值问题时,忽略二次项系数;
(2)在解决与二次函数有关的实际问题时,一是不能建立正确的函数关系缺乏建模思想;二是对自变量取值范围的忽略;
(3)对于二次函数的最值问题,误认为自变量取对称轴与 的交点时,函数值有最值.第36课时 二次函数综合题真题演练?层层推进
1.(2012广东珠海)如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.第36课时 二次函数综合题【答案】
(1)将点A(1,0)代入y=(x﹣2)2+m得,(1﹣2)2+m=0,解得m=﹣1,
∴二次函数解析式为y=(x﹣2)2﹣1,
当x=0时,y=4﹣1=3,∴C点坐标为(0,3),
∵二次函数y=(x﹣2)2﹣1的对称轴为x=2, C和B关于对称轴对称,
∴B点坐标为(4,3),
将A(1,0)、B(4,3)代入y=kx+b得,
,解得 ,
∴一次函数解析式为y=x﹣1;
(2)∵A、B坐标为(1,0),(4,3),
∴当kx+b≥(x﹣2)2+m时,直线y=x﹣1的图象在二次函数y=(x﹣2)2﹣1的图象上方或相交,此时1≤x≤4.
第36课时 二次函数综合题2.(2012广东)如图,抛物线y= x2- x-9与x轴交于A、B两点,与y轴交于点C,连接BC、AC.
(1)求AB和OC的长;
(2)点E从点A出发,沿x轴向点B运动(点E与点A、B不重合),过点E作直线l平行BC,交AC于点D.设AE的长为m,△ADE的面积为s,求s关于m的函数关系式,并写出自变量m的取值范围;
(3)在(2)的条件下,连接CE,求△CDE面积的最大值;此时,求出以点E为圆心,与BC相切的圆的面积(结果保留π).第36课时 二次函数综合题【答案】
(1)在y= x2- x-9中,
令x=0,得y=-9,∴C(0,﹣9);
令y=0,即 x2- x-9 ,解得:x1=﹣3,x2=6,
∴A(﹣3,0)、B(6,0),∴AB=9,OC=9。
(2)∵ED∥BC,∴△AED∽△ABC,∴ ,即: ,
∴s= m2(0<m<9)。第36课时 二次函数综合题【答案】
(3)∵S△AEC= AE?OC= m,S△AED =s= m2,
∴S△EDC=S△AEC﹣S△AED= 。
∴△CDE的最大面积为 ,
此时,AE=m= ,BE=AB﹣AE= 。
又 ,
过E作EF⊥BC于F,则Rt△BEF∽Rt△BCO,得: ,
即: 。
∴ 。
∴以E点为圆心,与BC相切的圆的面积 S⊙E=π?EF2= 。第36课时 二次函数综合题3.(2012广州)如图,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C.
(1)求点A、B的坐标;
(2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标;
(3)若直线l过点E(4,0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有三个时,求直线l的解析式.【答案】
(1)在 中,令y=0,即 ,
解得x1=﹣4,x2=2。
∵点A在点B的左侧,
∴A、B点的坐标为A(﹣4,0)、B(2,0);第36课时 二次函数综合题【答案】
(2)由 得,对称轴为x=-1.
在 中,令x=0,得y=3.
∴OC=3,AB=6, .
在Rt△AOC中,
设△ACD中AC边上的高为h,则有 AC?h=9,解得h= 。
如图1,在坐标平面内作直线平行于AC,且到AC的距离=h= ,这样的直线有2条,分别是L1和L2,则直线与对称轴x=﹣1的两个交点即为所求的点D
设L1交y轴于E,过C作CF⊥L1于F,则CF=h= ,
∴ 。第36课时 二次函数综合题【答案】
(2)(接上页)
设直线AC的解析式为y=kx+b,
将A(﹣4,0),B(0,3)坐标代入,得
,解得 。
∴直线AC解析式为y= x+3。
直线L1可以看做直线AC向下平移CE长度单位( 个长度单位)而形成的,
∴直线L1的解析式为 ,
则D1的纵坐标为 。∴D1(﹣4, ),
同理,直线AC向上平移 个长度单位得到L2,可求得D2(﹣1, ),
综上所述,D点坐标为:D1(﹣4, ),D2(﹣1, );第36课时 二次函数综合题【答案】(3)如图2,以AB为直径作⊙F,圆心为F.
过E点作⊙F的切线,这样的切线有2条.
连接FM,过M作MN⊥x轴于点N,
∵A(﹣4,0),B(2,0),∴F(﹣1,0),
⊙F半径FM=FB=3,又FE=5,
则在Rt△MEF中,ME= ,sin∠MFE= ,cos∠MFE= ,
在Rt△FMN中,MN=MN?sin∠MFE=3× = ,
FN=MN?cos∠MFE=3× = ,
则ON= 。∴M点坐标为( , ),
直线l过M( , ),E(4,0),
设直线l的解析式为y=k1x+b1,则有 ,解得 ,
∴直线l的解析式为y= x+3,
同理,可以求得另一条切线的解析式为y= x﹣3,
综上所述,直线l的解析式为y= x+3或y= x﹣3.第36课时 二次函数综合题4.(2014深圳)如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).
(1)求抛物线的解析式;
(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,
①求当△BEF与△BAO相似时,E点坐标;
②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.第36课时 二次函数综合题【答案】
(1)直线AB的解析式为y=2x+4,
令x=0,得y=4;令y=0,得x=﹣2.
∴A(﹣2,0)、B(0,4).
∵抛物线的顶点为点A(﹣2,0),
∴设抛物线的解析式为:y=a(x+2)2,
点C(0,﹣4)在抛物线上,代入上式得:﹣4=4a,解得a=﹣1,
∴抛物线的解析式为y=﹣(x+2)2.第36课时 二次函数综合题【答案】
(2)平移过程中,设点E的坐标为(m,2m+4),
则平移后抛物线的解析式为:y=﹣(x﹣m)2+2m+4,
∴F(0,﹣m2+2m+4).
①∵点E为顶点,∴∠BEF≥90°,
∴若△BEF与△BAO相似,只能是点E作为直角顶点,
∴△BAO∽△BFE,
∴ ,即 ,可得:BE=2EF.
如答图2﹣1,过点E作EH⊥y轴于点H,则点H坐标为:H(0,2m+4).
∵B(0,4),H(0,2m+4),F(0,﹣m2+2m+4),
∴BH=|2m|,FH=|﹣m2|.
在Rt△BEF中,由相似三角形性质得:BE2=BH?BF,EF2=FH?BF,第36课时 二次函数综合题【答案】
(2)又∵BE=2EF,∴BH=4FH,
即:4|﹣m2|=|2m|.
若﹣4m2=2m,解得m=- 或m=0(与点B重合,舍去);
若﹣4m2=﹣2m,解得m= 或m=0(与点B重合,舍去),此时点E位于第一象限,∠BEF为钝角,故此情形不成立.
∴m=- ,∴E(- ,3).
②假设存在.联立抛物线:y=﹣(x+2)2与直线AB:y=2x+4,
可求得:D(﹣4,﹣4),∴S△ACD= ×4×4=8,
∵S△EFG与S△ACD存在8倍的关系,∴S△EFG=64或S△EFG=1.
联立平移抛物线:y=﹣(x﹣m)2+2m+4与直线AB:y=2x+4,
可求得:G(m﹣2,2m).
∴点E与点M横坐标相差2,即: .第36课时 二次函数综合题【答案】
(2)如答图2﹣2,S△EFG =S△BFG ﹣S△BEF
= BF? ﹣ BF = BF?( )=BF.
∵B(0,4),F(0,﹣m2+2m+4),∴BF=|﹣m2+2m|.
∴|﹣m2+2m|=64或|﹣m2+2m|=1,
∴﹣m2+2m可取值为:64、﹣64、1、﹣1.
当取值为64时,一元二次方程﹣m2+2m=64无解,故﹣m2+2m≠64.
∴﹣m2+2m可取值为:﹣64、1、﹣1.
∵F(0,﹣m2+2m+4),
∴F坐标为:(0,﹣60)、(0,3)、(0,5).
综上所述,S△EFG与S△ACD存在8倍的关系,点F坐标为(0,﹣60)、(0,3)、(0,5).第36课时 二次函数综合题课时作业一、选择题
1.抛物线y=2x2,y=-2x2,y= x2共有的性质是( )
A.开口向下 B.对称轴是y轴 C.都有最低点 D. 随x的增大而减小2.对于二次函数y=(x-1)2+2的图象,下列说法正确的是( )
A.开口向下 B.对称轴是x=-1
C.顶点坐标中(1,2) D.与x轴有两个交点3.二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
A.函数有最小值 B.对称轴是x=
C.当x< 时, 随x的增大而减小
D.当-1
其中,正确结论的个数是( )
A.0 B.1 C.2 D.35.已知a、h、k为三数,且二次函数y=a(x-h)2+k在坐标平面上的图形通过(0,5)、(10,8)两点.若a<0,0<h<10,则h之值可能为下列何者?( )
A.1 B.3 C.5 D.7DD第36课时 二次函数综合题课时作业二、填空题
6.抛物线y=x2-2x+3的顶点坐标是 .7.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当y<5时,x的取值范围是 .8.如图,对称轴平行于y轴的抛物线与x轴交于(1,0),(3,0)两点,則它的对称轴为 .9.如图,抛物线y=ax2+bx+c的对称轴x=1,若点P(4,0)在该抛物线上,则4a-2b+c的值为 .(1,2)0<x<4x=20第36课时 二次函数综合题课时作业10.“如果二次函数y=ax2+bx+c的图象与x轴有两个公共点,那么一元二次方程ax2+bx+c=0有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:
若m,n(m
(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,
试判断点A′是否为该函数图象的顶点?第36课时 二次函数综合题课时作业【答案】
(1)抛物线的对称轴为x=1;
(2)点A′是该函数图象的顶点.理由如下:
由(1)可知,抛物线 的顶点坐标为(1, ),
如图,作A′B⊥x轴于点B,
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=2,
在Rt△A′OB中,∠OA′B=30°,
∴OB= OA′=1,
∴A′B= OB= ,
∴A′点的坐标为(1, ),
∴点A′为抛物线 的顶点.第36课时 二次函数综合题课时作业12.二次函数图象的顶点在原点O,经过点A ;点F(0,1)在y轴上.直线 y=-1与y轴交于点H.
(1)求二次函数的解析式;
(2)点P是(1)中图象上的点,过点P作x轴的垂线与直线y=-1交于点M,求证:FM平分∠OFP;
(3)当△FPM是等边三角形时,求P点的坐标.第36课时 二次函数综合题课时作业【答案】
(1)解:∵二次函数图象的顶点在原点O,
∴设二次函数的解析式为y=ax2,
将点A(1, )代入y=ax2得,a= ,
∴二次函数的解析式为y= x2;
(2)证明:∵点P在抛物线y= x2上,
∴可设点P的坐标为(x, x2) ,
如图,过点P作PB⊥y轴于点B,则BF= x2-1,PB=x,
∴Rt△BPF中,PF= = x2+1,
∴PM= x2+1,
∴PF=PM,∴∠PFM=∠PMF,
又∵PM∥x轴,∴∠MFH=∠PMF,∴∠PFM=∠MFH,
∴FM平分∠OFP;第36课时 二次函数综合题课时作业【答案】
(3)解:当△FPM是等边三角形时,∠PMF=60°,
∴∠FMH=30°,
在Rt△MFH中,MF=2FH=2×2=4,
∵PF=PM=FM,
∴ x2+1=4,
解得:x=±2 ,
∴ x2= ×12=3 ,
∴满足条件的点P的坐标为(-2 ,3) 或(2 ,3).第36课时 二次函数综合题课时作业13.如图,抛物线y=-x2+2x+c与x轴交于A,B两点,它的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F,已知点A的坐标为(-1,0).
(1)求该抛物线的解析式及顶点M的坐标.
(2)求△EMF与△BNE的面积之比.【答案】
(1)将A(-1,0)代入y=-x2+2x+c,得c=3,
∴抛物线的解析式为y=-x2+2x+3,
∵ y=-x2+2x+3=-(x-1)2+4
∴抛物线的顶点坐标为(1,4);
(2)∵A(-1,0),抛物线的对称轴为直线x=1,
∴点B(3,0),∴EM=1,BN=2,
∵EM∥BN, ∴△EMF∽△BNF,
∴ 第36课时 二次函数综合题课时作业14.九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x<50)天的售价与销量的相关信息如下表:
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
第36课时 二次函数综合题课时作业【答案】
(1)当1≤x<50时,y=(200-2x)(x+40-30)=-2x2+180x=200
当50≤x≤90时,y=(200-2x)(90-30)=-120x+12000;
(2)当1≤x<50时,将二次函数配方:y=-2x2+180x+200=-2(x-45)2+6050
∴当x=45时,y有最大值,最大值为6050;
当50≤x≤90时,函数y=-120x+12000是一次函数,y随x的增大而减小,
当x=50时,y有最大值,y最大值为6000;
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
(3)当y=4800时,对于-2(x-45)2+6050=4800,有x=20或x=60
∴当20≤x≤50时,y≥4800;
当y=4800时,对于120x+12000≥4800,有x≤60;
综上所述,当20≤x≤60时,每天销售利润不低于4800元.
结束谢谢!
同课章节目录
