广东省2015中考数学冲刺复习课件:第34课时 概率初步(共23张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第34课时 概率初步(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 678.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | |||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:04:23 | ||
图片预览





文档简介
课件23张PPT。数学
第34课时 概率初步第34课时 概率初步知识考点?对应精练
考点分类一 概率概念
【知识考点】
1、概率:一个事件发生的可能性的大小,可以用一个数来表示,我们把这个数叫做这个事件发生的概率.
2、频率:在进行试验的时候,当试验的次数很大时,某个事件发生的频率稳定在相应的概率附近.我们可以通过多次试验用一个事件的频率来估计这一事件的概率.
3、概率的计算
公式:P(A)=
列举法:①画树形图法;②列表法.第34课时 概率初步【知识考点】
4、一般地,当事件A为必然事件时,P(A)=1;
当事件A为不可能事件时,P(A)=0;
当事件A为随机事件时,0<P(A)<1.
总之,任何事件A发生的概率P(A)都是0和1之间(包括0和1)的数,即0≤P(A)≤1.【对应精练】
1.用长分别为5 cm,6 cm,7 cm的三条线段围成三角形的事件是( )
A.随机事件 B.必然事件 C.不可能事件 D.以上都不是
2.在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是( )
A. B. C. D.BB第34课时 概率初步考点分类二
【知识考点】
1.画树形图是列举随机事件的所有可能结果的重要方法之一,通过树形图,把所有可能的结果一一列出,有利于帮助我们分析问题,并且可以避免出现重复和遗漏,既形象直观又条理分明.
2.列表法也是列举随机事件的所有可能结果的一个重要的方法.第34课时 概率初步【对应精练】
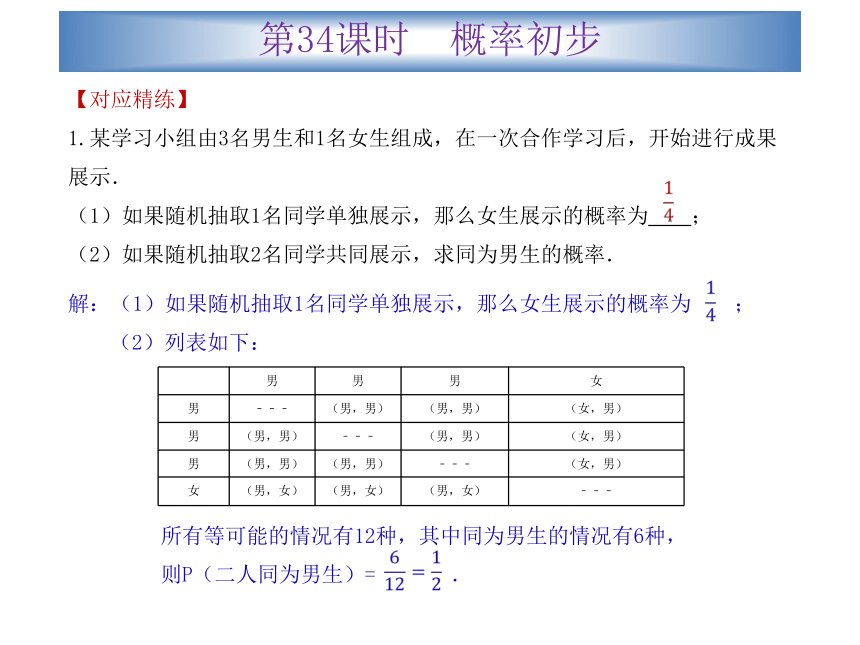
1.某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.解:(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)列表如下:
所有等可能的情况有12种,其中同为男生的情况有6种,
则P(二人同为男生)= .第34课时 概率初步【对应精练】
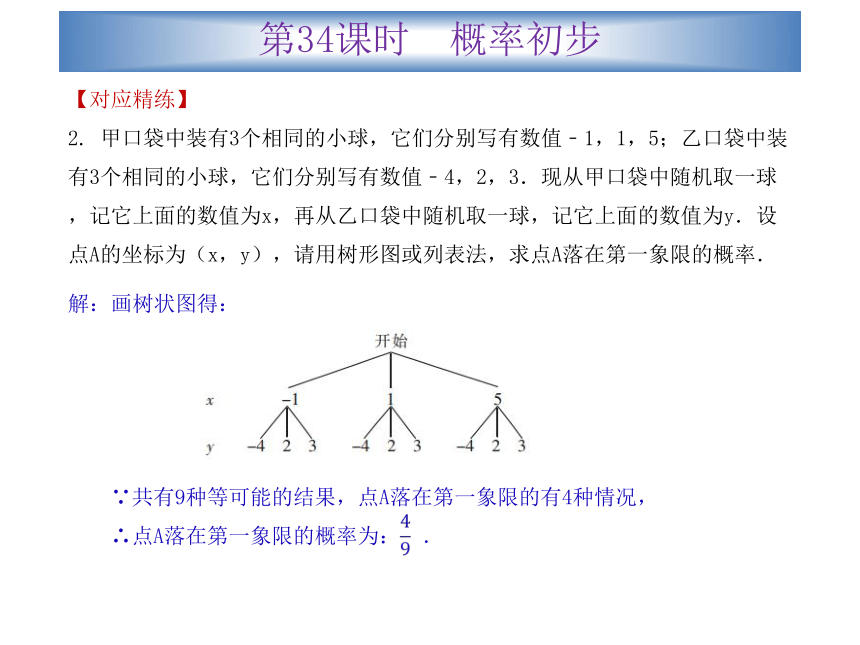
2. 甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.解:画树状图得:
∵共有9种等可能的结果,点A落在第一象限的有4种情况,
∴点A落在第一象限的概率为: .第34课时 概率初步真题演练?层层推进
基础题
(深圳市?2013年)写有“中国”、“美国”、“英国”、“韩国”的四张卡片,从中随机抽取一张,抽到卡片所对应的国家为亚洲的概率是( )
A. B. C. D. 12. (湛江?2013年)(四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片是轴对称图形的概率是( )
平行四边形 等腰梯形 圆 三角形
A. B. C. D.1AA第34课时 概率初步3. (佛山?2013年)掷一枚有正反面的均匀硬币,正确的说法是( )
A.正面一定朝上 B.反面一定朝上
C.正面比反面朝上的概率大 D.正面和反面朝上的概率都是0.54.(佛山?2013年)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是 .D提示:∵掷一枚有正反面的均匀硬币,∴正面和反面朝上的概率都是0.5.
故选:D.提示:根据题意画出树状图如下:
一共有12种情况,组成的两位数大于40的情况有3种,所以,P(组成的两位数大于40)= = .第34课时 概率初步5、(广东?2014年)一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.解:(1)列表
∴共有9种等可能结果。
(2)∴数字和为偶数的有5种,∴P(和为偶数)= 第34课时 概率初步提高题
6、(广东湛江?2013年) 把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上数字1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中各随机投取一张.
(1)试求取出的两张卡片数字之和为奇数概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.解:(1)用树状图列出所有的可能的情形如下:
从树状图可看出一共有9种等可能事件,和为偶数有4种情形,
所以 P(和为奇数)=
(2)由于 P(和为偶数)=1- = ,所以这个游戏不公平.第34课时 概率初步7. (2013珠海)把分别标有数字2、3、4、5的四个小球放入A袋内,把分别标有数字 、 、 、 、 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明.
(1)小明分别从A、B两个袋子中各摸出一个小球,求这两个球上的数字互为倒数的概率;
(2)当B袋中标有 的小球上的数字变为 时(填写所有结果),(1)中的概率为 .解:(1)列表如下:
有表可知,所有可能出现的结果共有20种,它们出现的可性相同,其中两个球上的数字互为倒数的有4种,所有P(两个球上的数字互为倒数)= = .
(2) 或 或 或 .
第34课时 概率初步拔高题
8. (四川成都?2013年) “中国梦”关乎每个人的幸福生活, 为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品. 现将参赛的50件作品的成绩(单位:分)进行统计如下:
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为_______,y的值为________.
(2)将本次参赛作品获得A等级的学生一次用A1,A2,A3,…表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.第34课时 概率初步解:(1)4, 0.7
(2)共有四名A等学生,列表如下
由图可知:共有12种等可能情况。刚好是A1和A2的有二种。
∴ P(A1和A2)= = 第34课时 概率初步课时作业一、选择题
1.(2014年广东卷)一个不透明的布袋里装有7个只有颜色不同的球,其中3个红球,4个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )2. (2014年江苏徐州)抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率( )3. (2013福建厦门).掷一个质地均匀的正方体骰子,当骰子停止后,朝上一面的点数为5的概率是( )
A.1. B. . C. . D.0.BBC第34课时 概率初步课时作业5.( 2014?深圳)袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )提示:画树状图得:
∵共有16种等可能的结果,抽取的两个球数字之和大于6的有10种情况,
∴抽取的两个球数字之和大于6的概率是: . 4. 下列事件属于必然事件的是( )
A.在1个标准大气压下,水加热到100 ℃沸腾
B.明天我市最高气温为56 ℃
C.中秋节晚上能看到月亮
D.下雨后有彩虹AC第34课时 概率初步课时作业7. (2013?泸州)在一只不透明的口袋中放入红球6个,黑球2个,黄球n个。这些球除颜色不同外,其它无任何差别,搅匀后随机从中摸出一个恰好是黄球的概率为 ,则放入口袋中的黄球总数n= .提示:∵桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,
∴现在从桶里随机摸出一个球,则摸到白球的概率为: .
故答案为: .二、填空题
6. (2014?珠海)桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,现在从桶里随机摸出一个球,则摸到白球的概率为 .48. (2013山东滨州)若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为 .第34课时 概率初步课时作业10.(2013?北京)在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率为 .提示:大于2的有3、4、5,共3个,故所求概率为 9.(2013,娄底)课间休息,小亮与小明一起玩“剪刀、石头、布”的游戏,小明出“剪刀”的概率是 。第34课时 概率初步课时作业三、解答题
11.(2014年广州市)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.解:至多有一名女生包括两种情况有1个或者0个女生
列表图:
由表可知,共有20种等可能情况,其中只有1个女生的情况:12种 ,有0个女生的情况:6种 ∴至多有一名女生包括两种情况18种
∴P(至多有一名女生)= =0.90第34课时 概率初步课时作业12. (2013福建厦门).有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面上只有一个整数且每个面上的整数互不相同).投掷这个正12面体一次,记事件A为 “向上一面的数字是2或3的整数倍”,记事件B为 “向上一面的数字是3的整数倍”,请你判断等式“P(A)= +P(B)”是否成立,并说明理由.解:等式不成立
∵ P(A)= ,
又∵P(B) = ,
而 .
∴ 等式不成立.第34课时 概率初步课时作业13. (2014年重庆市)为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:
(1)某镇今年1﹣5月新注册小型企业一共有 家.请将折线统计图补充完整;
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.第34课时 概率初步课时作业解:(1)根据统计图可知,3月份有4家,占25%,所以某镇今年1﹣5月新注册小型企业一共有:4÷25%=16(家),1月份有:16﹣2﹣4﹣3﹣2=5(家).折线统计图补充如下:
(2)设该镇今年3月新注册的小型企业为甲、乙、丙、丁,其中甲、乙为餐饮企业.画树状图得:
∵共有12种等可能的结果,甲、乙2家企业恰好被抽到的有2种,
∴P(2家企业恰好都是餐饮企业)= .第34课时 概率初步课时作业14. (2014?泉州)在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)随机地从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次取出相同颜色球的概率.解:(1)∵在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别,
∴随机地从箱子里取出1个球,则取出红球的概率是: ;
(2)画树状图得:
∵共有9种等可能的结果,两次取出相同颜色球的有3种情况,
∴P(两次取出相同颜色球)= = .结束谢谢!
考点分类一 概率概念
【知识考点】
1、概率:一个事件发生的可能性的大小,可以用一个数来表示,我们把这个数叫做这个事件发生的概率.
2、频率:在进行试验的时候,当试验的次数很大时,某个事件发生的频率稳定在相应的概率附近.我们可以通过多次试验用一个事件的频率来估计这一事件的概率.
3、概率的计算
公式:P(A)=
列举法:①画树形图法;②列表法.第34课时 概率初步【知识考点】
4、一般地,当事件A为必然事件时,P(A)=1;
当事件A为不可能事件时,P(A)=0;
当事件A为随机事件时,0<P(A)<1.
总之,任何事件A发生的概率P(A)都是0和1之间(包括0和1)的数,即0≤P(A)≤1.【对应精练】
1.用长分别为5 cm,6 cm,7 cm的三条线段围成三角形的事件是( )
A.随机事件 B.必然事件 C.不可能事件 D.以上都不是
2.在10个外观相同的产品中,有2个不合格产品,现从中任意抽取1个进行检测,抽到不合格产品的概率是( )
A. B. C. D.BB第34课时 概率初步考点分类二
【知识考点】
1.画树形图是列举随机事件的所有可能结果的重要方法之一,通过树形图,把所有可能的结果一一列出,有利于帮助我们分析问题,并且可以避免出现重复和遗漏,既形象直观又条理分明.
2.列表法也是列举随机事件的所有可能结果的一个重要的方法.第34课时 概率初步【对应精练】
1.某学习小组由3名男生和1名女生组成,在一次合作学习后,开始进行成果展示.
(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)如果随机抽取2名同学共同展示,求同为男生的概率.解:(1)如果随机抽取1名同学单独展示,那么女生展示的概率为 ;
(2)列表如下:
所有等可能的情况有12种,其中同为男生的情况有6种,
则P(二人同为男生)= .第34课时 概率初步【对应精练】
2. 甲口袋中装有3个相同的小球,它们分别写有数值﹣1,1,5;乙口袋中装有3个相同的小球,它们分别写有数值﹣4,2,3.现从甲口袋中随机取一球,记它上面的数值为x,再从乙口袋中随机取一球,记它上面的数值为y.设点A的坐标为(x,y),请用树形图或列表法,求点A落在第一象限的概率.解:画树状图得:
∵共有9种等可能的结果,点A落在第一象限的有4种情况,
∴点A落在第一象限的概率为: .第34课时 概率初步真题演练?层层推进
基础题
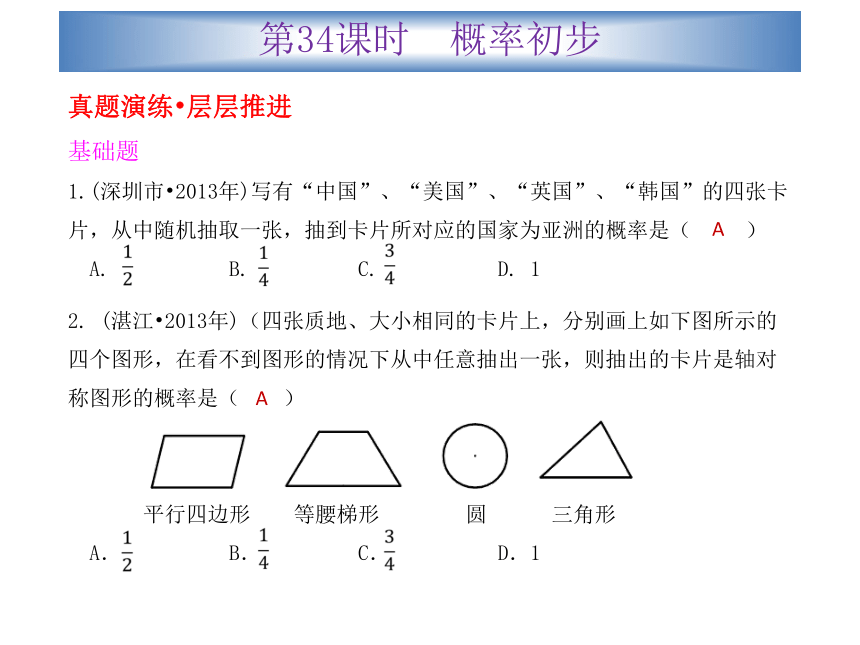
(深圳市?2013年)写有“中国”、“美国”、“英国”、“韩国”的四张卡片,从中随机抽取一张,抽到卡片所对应的国家为亚洲的概率是( )
A. B. C. D. 12. (湛江?2013年)(四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片是轴对称图形的概率是( )
平行四边形 等腰梯形 圆 三角形
A. B. C. D.1AA第34课时 概率初步3. (佛山?2013年)掷一枚有正反面的均匀硬币,正确的说法是( )
A.正面一定朝上 B.反面一定朝上
C.正面比反面朝上的概率大 D.正面和反面朝上的概率都是0.54.(佛山?2013年)在1,2,3,4四个数字中随机选两个不同的数字组成两位数,则组成的两位数大于40的概率是 .D提示:∵掷一枚有正反面的均匀硬币,∴正面和反面朝上的概率都是0.5.
故选:D.提示:根据题意画出树状图如下:
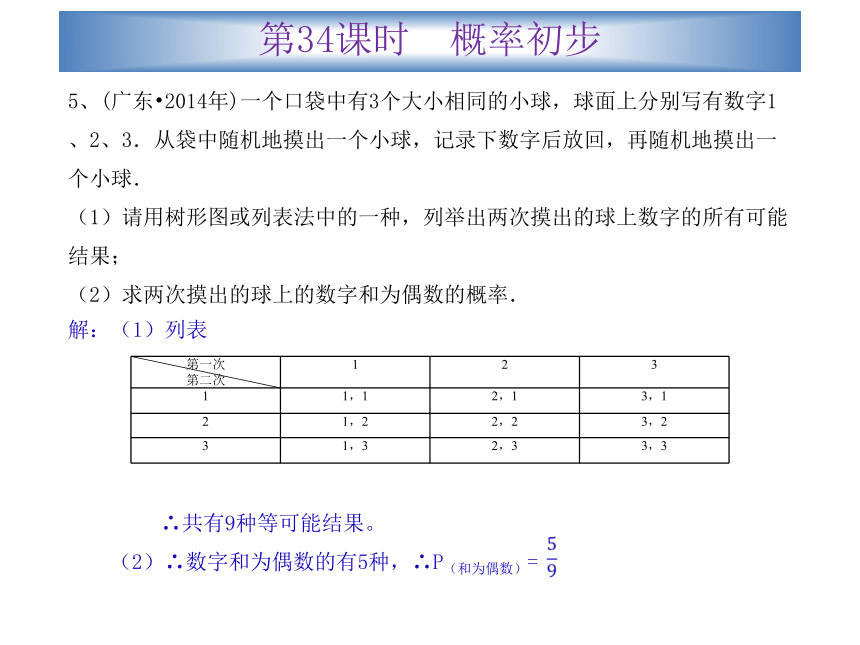
一共有12种情况,组成的两位数大于40的情况有3种,所以,P(组成的两位数大于40)= = .第34课时 概率初步5、(广东?2014年)一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.解:(1)列表
∴共有9种等可能结果。
(2)∴数字和为偶数的有5种,∴P(和为偶数)= 第34课时 概率初步提高题
6、(广东湛江?2013年) 把大小和形状完全相同的6张卡片分成两组,每组3张,分别标上数字1、2、3,将这两组卡片分别放入两个盒子中搅匀,再从中各随机投取一张.
(1)试求取出的两张卡片数字之和为奇数概率;
(2)若取出的两张卡片数字之和为奇数,则甲胜;取出的两张卡片数字之和为偶数,则乙胜;试分析这个游戏是否公平?请说明理由.解:(1)用树状图列出所有的可能的情形如下:
从树状图可看出一共有9种等可能事件,和为偶数有4种情形,
所以 P(和为奇数)=
(2)由于 P(和为偶数)=1- = ,所以这个游戏不公平.第34课时 概率初步7. (2013珠海)把分别标有数字2、3、4、5的四个小球放入A袋内,把分别标有数字 、 、 、 、 的五个小球放入B袋内,所有小球的形状、大小、质地完全相同,A、B两个袋子不透明.
(1)小明分别从A、B两个袋子中各摸出一个小球,求这两个球上的数字互为倒数的概率;
(2)当B袋中标有 的小球上的数字变为 时(填写所有结果),(1)中的概率为 .解:(1)列表如下:
有表可知,所有可能出现的结果共有20种,它们出现的可性相同,其中两个球上的数字互为倒数的有4种,所有P(两个球上的数字互为倒数)= = .
(2) 或 或 或 .
第34课时 概率初步拔高题
8. (四川成都?2013年) “中国梦”关乎每个人的幸福生活, 为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以“梦想中国,逐梦成都”为主题的摄影大赛,要求参赛学生每人交一件作品. 现将参赛的50件作品的成绩(单位:分)进行统计如下:
请根据上表提供的信息,解答下列问题:
(1)表中的x的值为_______,y的值为________.
(2)将本次参赛作品获得A等级的学生一次用A1,A2,A3,…表示,现该校决定从本次参赛作品中获得A等级学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生A1和A2的概率.第34课时 概率初步解:(1)4, 0.7
(2)共有四名A等学生,列表如下
由图可知:共有12种等可能情况。刚好是A1和A2的有二种。
∴ P(A1和A2)= = 第34课时 概率初步课时作业一、选择题
1.(2014年广东卷)一个不透明的布袋里装有7个只有颜色不同的球,其中3个红球,4个白球,从布袋中随机摸出一个球,摸出的球是红球的概率是( )2. (2014年江苏徐州)抛掷一枚均匀的硬币,前2次都正面朝上,第3次正面朝上的概率( )3. (2013福建厦门).掷一个质地均匀的正方体骰子,当骰子停止后,朝上一面的点数为5的概率是( )
A.1. B. . C. . D.0.BBC第34课时 概率初步课时作业5.( 2014?深圳)袋子里有4个球,标有2,3,4,5,先抽取一个并记住,放回,然后再抽取一个,所抽取的两个球数字之和大于6的概率是( )提示:画树状图得:
∵共有16种等可能的结果,抽取的两个球数字之和大于6的有10种情况,
∴抽取的两个球数字之和大于6的概率是: . 4. 下列事件属于必然事件的是( )
A.在1个标准大气压下,水加热到100 ℃沸腾
B.明天我市最高气温为56 ℃
C.中秋节晚上能看到月亮
D.下雨后有彩虹AC第34课时 概率初步课时作业7. (2013?泸州)在一只不透明的口袋中放入红球6个,黑球2个,黄球n个。这些球除颜色不同外,其它无任何差别,搅匀后随机从中摸出一个恰好是黄球的概率为 ,则放入口袋中的黄球总数n= .提示:∵桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,
∴现在从桶里随机摸出一个球,则摸到白球的概率为: .
故答案为: .二、填空题
6. (2014?珠海)桶里原有质地均匀、形状大小完全一样的6个红球和4个白球,小红不慎遗失了其中2个红球,现在从桶里随机摸出一个球,则摸到白球的概率为 .48. (2013山东滨州)若从长度分别为3、5、6、9的四条线段中任取三条,则能组成三角形的概率为 .第34课时 概率初步课时作业10.(2013?北京)在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5,从中随机摸出一个小球,其标号大于2的概率为 .提示:大于2的有3、4、5,共3个,故所求概率为 9.(2013,娄底)课间休息,小亮与小明一起玩“剪刀、石头、布”的游戏,小明出“剪刀”的概率是 。第34课时 概率初步课时作业三、解答题
11.(2014年广州市)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.解:至多有一名女生包括两种情况有1个或者0个女生
列表图:
由表可知,共有20种等可能情况,其中只有1个女生的情况:12种 ,有0个女生的情况:6种 ∴至多有一名女生包括两种情况18种
∴P(至多有一名女生)= =0.90第34课时 概率初步课时作业12. (2013福建厦门).有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面上只有一个整数且每个面上的整数互不相同).投掷这个正12面体一次,记事件A为 “向上一面的数字是2或3的整数倍”,记事件B为 “向上一面的数字是3的整数倍”,请你判断等式“P(A)= +P(B)”是否成立,并说明理由.解:等式不成立
∵ P(A)= ,
又∵P(B) = ,
而 .
∴ 等式不成立.第34课时 概率初步课时作业13. (2014年重庆市)为鼓励创业,市政府制定了小型企业的优惠政策,许多小型企业应运而生,某镇统计了该镇1﹣5月新注册小型企业的数量,并将结果绘制成如下两种不完整的统计图:
(1)某镇今年1﹣5月新注册小型企业一共有 家.请将折线统计图补充完整;
(2)该镇今年3月新注册的小型企业中,只有2家是餐饮企业,现从3月新注册的小型企业中随机抽取2家企业了解其经营状况,请用列表或画树状图的方法求出所抽取的2家企业恰好都是餐饮企业的概率.第34课时 概率初步课时作业解:(1)根据统计图可知,3月份有4家,占25%,所以某镇今年1﹣5月新注册小型企业一共有:4÷25%=16(家),1月份有:16﹣2﹣4﹣3﹣2=5(家).折线统计图补充如下:
(2)设该镇今年3月新注册的小型企业为甲、乙、丙、丁,其中甲、乙为餐饮企业.画树状图得:
∵共有12种等可能的结果,甲、乙2家企业恰好被抽到的有2种,
∴P(2家企业恰好都是餐饮企业)= .第34课时 概率初步课时作业14. (2014?泉州)在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别.
(1)随机地从箱子里取出1个球,则取出红球的概率是多少?
(2)随机地从箱子里取出1个球,放回搅匀再取第二个球,请你用画树状图或列表的方法表示所有等可能的结果,并求两次取出相同颜色球的概率.解:(1)∵在一个不透明的箱子里,装有红、白、黑各一个球,它们除了颜色之外没有其他区别,
∴随机地从箱子里取出1个球,则取出红球的概率是: ;
(2)画树状图得:
∵共有9种等可能的结果,两次取出相同颜色球的有3种情况,
∴P(两次取出相同颜色球)= = .结束谢谢!
同课章节目录
