广东省2015中考数学冲刺复习课件:第33课时 统计初步(共26张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第33课时 统计初步(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 975.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:05:04 | ||
图片预览







文档简介
课件26张PPT。数学
第33课时 统计初步第33课时 统计初步知识考点?对应精练
考点分类一 几种统计图
【知识考点】
1.条形统计图:用长方形的高来表示数据的图形.它的特点是:(1)能够显示每组中的具体数据;(2)易于比较各组数据之间的差别.
2.折线统计图:用几条线段连成的折线来表示数据的图形.它的特点是:易于显示数据的变化趋势
3.扇形统计图:
(1)用一个圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分在总体中所占百分比的大小,这样的统计图叫扇形统计图.
(2)百分比的意义:在扇形统计图中,每部分占总体的百分比等于该部分所对扇形的圆心角的度数与的比.
(3)扇形的圆心角=360°×百分比.第33课时 统计初步【知识考点】
4.频数分布直方图:
(1)统计数据中每个对象出现的次数叫频数,每个对象出现的次数与总次数的比值(或者百分比)叫频率,频数和频率都能够反映每个对象出现的频繁程度.
(2)频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的变化情况。【对应精练】
1. 如图是某足球队全年比赛情况统计图:
根据图中信息,该队全年胜了 场.提示:全年比赛场次=10÷25%=40,
胜场:40×(1﹣20%﹣25%)=40×55%=22场.22第33课时 统计初步【对应精练】
2、(2013深圳市).2013年起,深圳市实施行人闯红灯违法处罚,处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款100元”、“穿绿马甲维护交通”。下图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)实施首日,该片区行人闯红灯违法受处罚一共 人;
(2)在所有闯红灯违法受处罚的行人中, 穿绿马甲维护交通所占的百分比是 %;
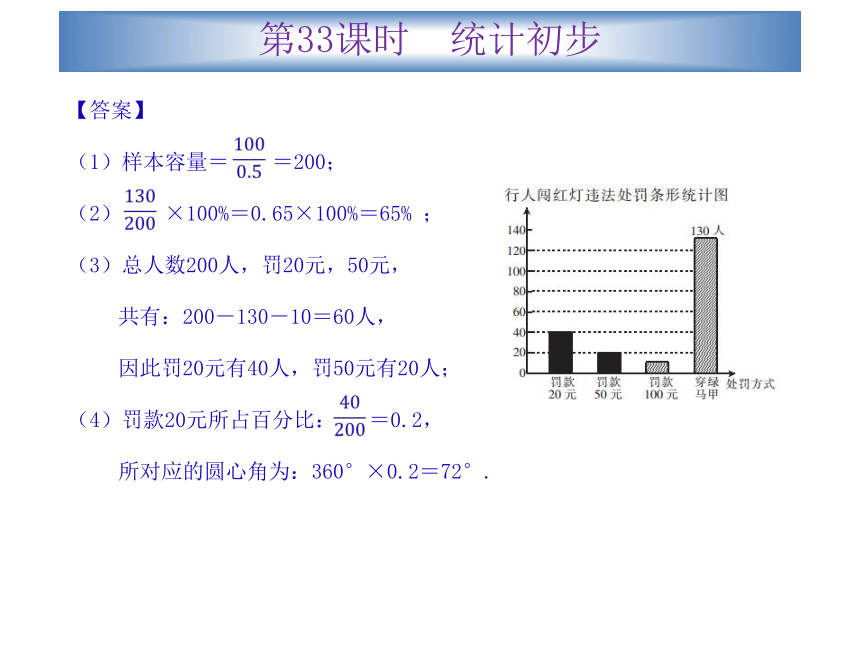
(3)据了解,“罚款20元”人数是“罚款50元”人数的2倍,请补全条形统计图;
(4)根据(3)中的信息,在扇形统计图中,“罚款20元”所在扇形的圆心角等于 度。第33课时 统计初步【答案】
(1)样本容量= =200;
(2) ×100%=0.65×100%=65% ;
(3)总人数200人,罚20元,50元,
共有:200-130-10=60人,
因此罚20元有40人,罚50元有20人;
(4)罚款20元所占百分比: =0.2,
所对应的圆心角为:360°×0.2=72°.第33课时 统计初步考点分类二 统计的几个概念:平均数、中位数、众数、方差
【知识考点】
1.总体、个体及样本
在统计中,我们把所要考察对象的全体叫做总体,其中每一个考察对象叫做个体.当总体中个体数目较多时,一般从总体中抽取一部分个体,这一部分个体叫做总体的样本,样本中个体的数目叫做样本容量.
2.平均数
如果有n个数x1,x2,x3,…,xn,那么 = (x1+x2+x3+…+xn)叫做这n个数的算术平均数,简称平均数.
若n个数x1,x2,x3,…,xn的权分别是ω1,ω2,ω3,…,ωn, 则 叫做这n个数的加权平均数.数据的权能够反映数据的相对“重要程度”.
总体中所有个体的平均数叫做总体平均数.样本中所有个体的平均数叫做样本平均数.通常用样本平均数去估计总体平均数,用样本估计总体时,样本越大,对总体的估计也就越精确.第33课时 统计初步【知识考点】
3.众数与中位数
(1)在一组数据中,出现次数最多的数叫做这组数据的众数(一组数据的众数有时有多个).
(2)将一组数据按大小依次排列,把处在最中间的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
(3)众数、中位数与平均数从不同的角度描述了一组数据的集中趋势.
4.方差、标准差与极差
(1)在一组数据x1,x2,x3,x4,…,xn中,各数据与它们的平均数 的差的平方的平均数叫做这组数据的方差,
即 .
(2)一组数据的方差的算术平方根叫做这组数据的标准差,即
s= .
(3)极差=最大值-最小值
(4)极差、方差和标准差都是用来衡量一组数据的波动大小的,方差(或标准差)越大,说明这组数据波动越大。第33课时 统计初步【对应精练】
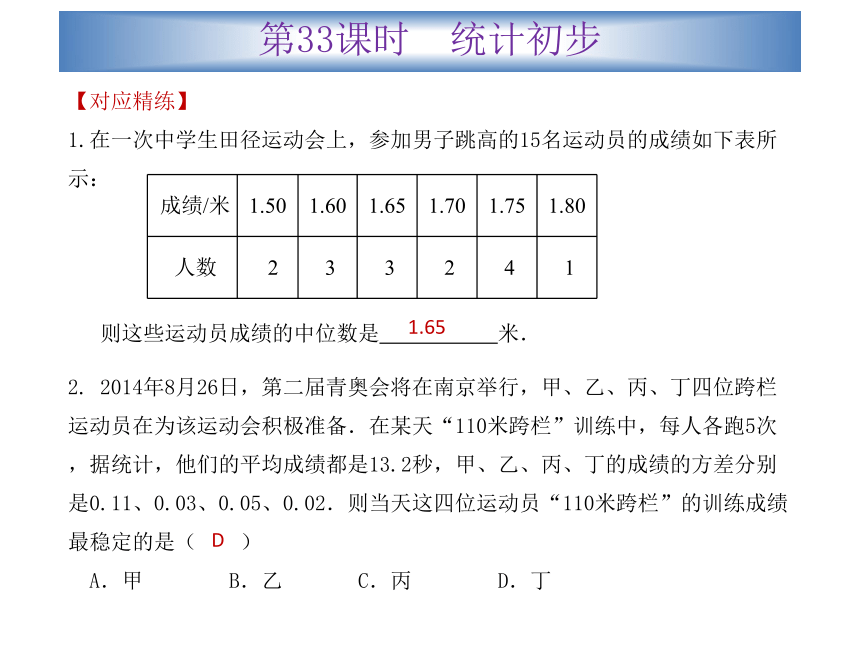
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
则这些运动员成绩的中位数是 米.2. 2014年8月26日,第二届青奥会将在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备.在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11、0.03、0.05、0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁1.65D第33课时 统计初步真题演练?层层推进
基础题
1. (广州市?2013年)为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式是( ),图中的a的值是( )
A. 全面调查,26 B. 全面调查,24
C. 抽样调查,26 D. 抽样调查,24提示:该调查方式是抽样调查,a=50﹣6﹣10﹣6﹣4=24,故选:D.DD第33课时 统计初步3. (广州市?2014年)在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( ).
(A)中位数是8 (B)众数是9 (C)平均数是8 (D)极差是7B2.(湛江?2013年)气候宜人的省级度假胜地吴川吉兆,测得一至五月份的平均气温分别为17、17、20、22、24(单位:℃),这组数据的中位数是( )
A.24 B.22 C.20 D.17C第33课时 统计初步解:(1)九年级(1)班中“很好”所占的比例为30%,“很好”的人数为18,所以九年级(1)班共有18÷30%=60(人).
(2)九年级(1)中“较好”的人数为30,所以“较好”所占的比例为30÷60=50%,所以“较差”的所占比例为1-30%-15%-50%=5%.所以对安全知识的了解情况为“较差”部分所对应的圆心角的度数是360°×5%=18°.
(3)全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有(5%+15%)×1500=300(人).18°300604.(梅州?2013年) “安全教育,警钟长鸣”,为此,某校随机抽取了九年级(1)班的学生对安全知识的了解情况进行了一次调查统计,图①和图②是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:(1)九年级(1)班共有 名学生;
(2)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是 ;
(3)若全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有 名第33课时 统计初步5.珠海?2013年) 某初中学校对全校学生进行一次“勤洗手”问卷调查,学校七、八、九三个年级学生分别为600、700、600人.经过数据整理,将全校的“勤洗手”调查数据绘制成统计图:
(1)根据统计图,计算八年级“勤洗手”学生人数,并补全下面的两幅统计图;
(2)通过计算说明哪个年级“勤洗手”学生人数占本年级学生人数的比例最大?第33课时 统计初步解:(1)300÷25%=1200(人),1200×35%=420(人).
所以八年级“勤洗手”学生人数为420人.
九年级占得百分比为1―25%―35%=40%.
补全两幅统计图如下:
(2)七年级“勤洗手”学生人数占本年级学生人数的比例为300÷600=50%,
八年级“勤洗手”学生人数占本年级学生人数的比例为420÷700=60%,
九年级“勤洗手”学生人数占本年级学生人数的比例为480÷600=80%,
所以九年级“勤洗手”学生人数占本年级学生人数的比例最大.第33课时 统计初步提高题
6. 深圳?2014年)关于体育选考项目统计图
(1)求出表中a,b,c的值,并将条形统计图补充完整.表中a= ,b= ,c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?解:(1)a=20÷0.1=200,
c=200×0.3=60,
b=80÷200=0.4,
故答案为:200,0.4,60,
补全条形统计图如下:
(2)30000×0.4=12000(人).
答:3万人参加体育选考,会有12000人选择篮球.2000.460第33课时 统计初步7.某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创造能力考察,他们的成绩(百分制)如下表:
(1)若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
(2)若公司根据经营性质和岗位要求认为:面试成绩中形体占5%,口才占30%,笔试成绩中专业水平占35%,创新能力占30%,那么你认为该公司应该录取谁?解:(1)甲、乙各自成绩分别为90.8,91.9,录取乙;
(2)甲、乙各自成绩分别为92.5,92.15,录取甲.第33课时 统计初步拔高题
8.(2014年江苏徐州)(利用统计结果作出选择)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9 乙:5,9,7,10,9
(1)填写下表:
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).解:(1)甲的众数为8,乙的平均数= (5+9+7+10+9)=8,乙的中位数为9;
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
故答案为:8,8,9;变小.第33课时 统计初步课时作业一、选择题
1.(2014?深圳)在﹣2,1,2,1,4,6中正确的是( )
A.平均数3 B.众数是﹣2 C.中位数是1 D.极差为8
2.(2013?深圳市)某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分 B.中位数 C.极差 D.平均数
提示:21个数的中位数即为第11名的成绩,对比第11名即知自己是否被录取。DB第33课时 统计初步课时作业3. (2014年云南省)学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
则入围同学决赛成绩的中位数和众数分别是( )
A. 9.70,9.60 B.9.60,9.60
C.9.60,9.70 D.9.65,9.60
提示:∵共有18名同学,
则中位数为第9名和第10名同学成绩的平均分,
即中位数为: =9.60,
众数为:9.60.
4.(2014年广西钦州)体育课上,两名同学分别进行了5次立定跳远测试,要判断这5次测试中谁的成绩比较稳定,通常需要比较这两名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差DB第33课时 统计初步课时作业5. (2014?无锡)已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数 B.标准差 C.中位数 D.众数B二、填空题
6.(2014年梅州)小明在射击训练中,五次命中的环数分别为5,7,6,6,6,则小明命中环数的众数为 ,平均数为 .
7.(2014?泉州)在综合实践课上,六名同学的作品数量(单位:件)分别为:3、5、2、5、5、7,则这组数据的众数为 件.
8. 在为灾区捐款中,各班的捐款数额如下(单位:元):99,101,103,97,102,96,104,95,105,100,则该校平均每班捐款为 .665100.2元第33课时 统计初步课时作业9. (2012?襄阳)在植树节当天,某校一个班同学分成10个小组参加植树造林活动,10个小组植树的株数见下表:则这10个小组植树株数的方差是 .
提示:根据表格得,平均数=(5×3+6×4+7×3)÷10=6
∴方差= 0.610. 某公司员工的月工资如下:580,650,880,900,1200,650,730,810
问:(1)公司所有员工的平均工资是 ;
(2)所有员工工资的中位数是 ;
(3)所有员工工资的众数是 ;
(4)用平均数还是中位数或是众数描述该公司员工工资的一般水平比较恰当,答 。800元770元650元中位数第33课时 统计初步课时作业三、解答题
11. (2014?珠海)某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.
(1)求该班的学生人数;
(2)若该校初三年级有1000人,估计该年级选考立定供远的人数.解:(1)根据题意得:30÷60%=50(人),则该校学生人数为50人;
(2)根据题意得:1000× =100(人),则估计该年级选考立定供远的人数为100人.第33课时 统计初步课时作业12.(2014年广东)某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如1图和题2图所示的不完整的统计图。
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调
查的所有学生一餐浪费的食物可以供200人用
一餐.据此估算,该校18 000名学生一餐浪费
的食物可供多少人食用一餐?解:(1)1000名;
(2)剩少量饭菜的人数为:
1000-(400+250+150)200(人).
(3) ×18000=3600(人)
答:估计可供3600人食用一餐。1000第33课时 统计初步课时作业13. (2014?绍兴)为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?第33课时 统计初步课时作业解:(1)根据题意得:a=1﹣(35%+25%+25%+10%)=5%;
(2)根据题意得:(6+19+17+10+8)×35%=21(人),
则抽取的样本中,八年级学生睡眠时间在C组的有21人;
(3)根据题意得:755× +785×(25%+35%)=453+471=924(人)
则该校七、八年级学生中睡眠时间合格的共有924人.第33课时 统计初步课时作业14.(2014?泉州)课外阅读是提高学生素养的重要途径.某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
(1)求表格中的a的值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
解:(1)50﹣10﹣20﹣15=5(名),故a的值为5,条形统计图如下:
(2)1300× =520(名),答:估计该校共有520名学生课外阅读时间不少于1小时.50名学生平均每天课外阅读时间统计表结束谢谢!
考点分类一 几种统计图
【知识考点】
1.条形统计图:用长方形的高来表示数据的图形.它的特点是:(1)能够显示每组中的具体数据;(2)易于比较各组数据之间的差别.
2.折线统计图:用几条线段连成的折线来表示数据的图形.它的特点是:易于显示数据的变化趋势
3.扇形统计图:
(1)用一个圆代表总体,圆中的各个扇形分别代表总体中的不同部分,扇形的大小反映部分在总体中所占百分比的大小,这样的统计图叫扇形统计图.
(2)百分比的意义:在扇形统计图中,每部分占总体的百分比等于该部分所对扇形的圆心角的度数与的比.
(3)扇形的圆心角=360°×百分比.第33课时 统计初步【知识考点】
4.频数分布直方图:
(1)统计数据中每个对象出现的次数叫频数,每个对象出现的次数与总次数的比值(或者百分比)叫频率,频数和频率都能够反映每个对象出现的频繁程度.
(2)频数分布表、频数分布直方图和频数折线图都能直观、清楚地反映数据在各个小范围内的变化情况。【对应精练】
1. 如图是某足球队全年比赛情况统计图:
根据图中信息,该队全年胜了 场.提示:全年比赛场次=10÷25%=40,
胜场:40×(1﹣20%﹣25%)=40×55%=22场.22第33课时 统计初步【对应精练】
2、(2013深圳市).2013年起,深圳市实施行人闯红灯违法处罚,处罚方式分为四类:“罚款20元”、“罚款50元”、“罚款100元”、“穿绿马甲维护交通”。下图是实施首日由某片区的执法结果整理数据后绘制的两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)实施首日,该片区行人闯红灯违法受处罚一共 人;
(2)在所有闯红灯违法受处罚的行人中, 穿绿马甲维护交通所占的百分比是 %;
(3)据了解,“罚款20元”人数是“罚款50元”人数的2倍,请补全条形统计图;
(4)根据(3)中的信息,在扇形统计图中,“罚款20元”所在扇形的圆心角等于 度。第33课时 统计初步【答案】
(1)样本容量= =200;
(2) ×100%=0.65×100%=65% ;
(3)总人数200人,罚20元,50元,
共有:200-130-10=60人,
因此罚20元有40人,罚50元有20人;
(4)罚款20元所占百分比: =0.2,
所对应的圆心角为:360°×0.2=72°.第33课时 统计初步考点分类二 统计的几个概念:平均数、中位数、众数、方差
【知识考点】
1.总体、个体及样本
在统计中,我们把所要考察对象的全体叫做总体,其中每一个考察对象叫做个体.当总体中个体数目较多时,一般从总体中抽取一部分个体,这一部分个体叫做总体的样本,样本中个体的数目叫做样本容量.
2.平均数
如果有n个数x1,x2,x3,…,xn,那么 = (x1+x2+x3+…+xn)叫做这n个数的算术平均数,简称平均数.
若n个数x1,x2,x3,…,xn的权分别是ω1,ω2,ω3,…,ωn, 则 叫做这n个数的加权平均数.数据的权能够反映数据的相对“重要程度”.
总体中所有个体的平均数叫做总体平均数.样本中所有个体的平均数叫做样本平均数.通常用样本平均数去估计总体平均数,用样本估计总体时,样本越大,对总体的估计也就越精确.第33课时 统计初步【知识考点】
3.众数与中位数
(1)在一组数据中,出现次数最多的数叫做这组数据的众数(一组数据的众数有时有多个).
(2)将一组数据按大小依次排列,把处在最中间的一个数据(或最中间两个数据的平均数)叫做这组数据的中位数.
(3)众数、中位数与平均数从不同的角度描述了一组数据的集中趋势.
4.方差、标准差与极差
(1)在一组数据x1,x2,x3,x4,…,xn中,各数据与它们的平均数 的差的平方的平均数叫做这组数据的方差,
即 .
(2)一组数据的方差的算术平方根叫做这组数据的标准差,即
s= .
(3)极差=最大值-最小值
(4)极差、方差和标准差都是用来衡量一组数据的波动大小的,方差(或标准差)越大,说明这组数据波动越大。第33课时 统计初步【对应精练】
1.在一次中学生田径运动会上,参加男子跳高的15名运动员的成绩如下表所示:
则这些运动员成绩的中位数是 米.2. 2014年8月26日,第二届青奥会将在南京举行,甲、乙、丙、丁四位跨栏运动员在为该运动会积极准备.在某天“110米跨栏”训练中,每人各跑5次,据统计,他们的平均成绩都是13.2秒,甲、乙、丙、丁的成绩的方差分别是0.11、0.03、0.05、0.02.则当天这四位运动员“110米跨栏”的训练成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁1.65D第33课时 统计初步真题演练?层层推进
基础题
1. (广州市?2013年)为了解中学生获取资讯的主要渠道,设置“A:报纸,B:电视,C:网络,D:身边的人,E:其他”五个选项(五项中必选且只能选一项)的调查问卷,先随机抽取50名中学生进行该问卷调查,根据调查的结果绘制条形图如图,该调查的方式是( ),图中的a的值是( )
A. 全面调查,26 B. 全面调查,24
C. 抽样调查,26 D. 抽样调查,24提示:该调查方式是抽样调查,a=50﹣6﹣10﹣6﹣4=24,故选:D.DD第33课时 统计初步3. (广州市?2014年)在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是:7,10,9,8,7,9,9,8.对这组数据,下列说法正确的是( ).
(A)中位数是8 (B)众数是9 (C)平均数是8 (D)极差是7B2.(湛江?2013年)气候宜人的省级度假胜地吴川吉兆,测得一至五月份的平均气温分别为17、17、20、22、24(单位:℃),这组数据的中位数是( )
A.24 B.22 C.20 D.17C第33课时 统计初步解:(1)九年级(1)班中“很好”所占的比例为30%,“很好”的人数为18,所以九年级(1)班共有18÷30%=60(人).
(2)九年级(1)中“较好”的人数为30,所以“较好”所占的比例为30÷60=50%,所以“较差”的所占比例为1-30%-15%-50%=5%.所以对安全知识的了解情况为“较差”部分所对应的圆心角的度数是360°×5%=18°.
(3)全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有(5%+15%)×1500=300(人).18°300604.(梅州?2013年) “安全教育,警钟长鸣”,为此,某校随机抽取了九年级(1)班的学生对安全知识的了解情况进行了一次调查统计,图①和图②是通过数据收集后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:(1)九年级(1)班共有 名学生;
(2)在扇形统计图中,对安全知识的了解情况为“较差”部分所对应的圆心角的度数是 ;
(3)若全校有1500名学生,估计对安全知识的了解情况为“较差”、“一般”的学生共有 名第33课时 统计初步5.珠海?2013年) 某初中学校对全校学生进行一次“勤洗手”问卷调查,学校七、八、九三个年级学生分别为600、700、600人.经过数据整理,将全校的“勤洗手”调查数据绘制成统计图:
(1)根据统计图,计算八年级“勤洗手”学生人数,并补全下面的两幅统计图;
(2)通过计算说明哪个年级“勤洗手”学生人数占本年级学生人数的比例最大?第33课时 统计初步解:(1)300÷25%=1200(人),1200×35%=420(人).
所以八年级“勤洗手”学生人数为420人.
九年级占得百分比为1―25%―35%=40%.
补全两幅统计图如下:
(2)七年级“勤洗手”学生人数占本年级学生人数的比例为300÷600=50%,
八年级“勤洗手”学生人数占本年级学生人数的比例为420÷700=60%,
九年级“勤洗手”学生人数占本年级学生人数的比例为480÷600=80%,
所以九年级“勤洗手”学生人数占本年级学生人数的比例最大.第33课时 统计初步提高题
6. 深圳?2014年)关于体育选考项目统计图
(1)求出表中a,b,c的值,并将条形统计图补充完整.表中a= ,b= ,c= .
(2)如果有3万人参加体育选考,会有多少人选择篮球?解:(1)a=20÷0.1=200,
c=200×0.3=60,
b=80÷200=0.4,
故答案为:200,0.4,60,
补全条形统计图如下:
(2)30000×0.4=12000(人).
答:3万人参加体育选考,会有12000人选择篮球.2000.460第33课时 统计初步7.某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创造能力考察,他们的成绩(百分制)如下表:
(1)若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
(2)若公司根据经营性质和岗位要求认为:面试成绩中形体占5%,口才占30%,笔试成绩中专业水平占35%,创新能力占30%,那么你认为该公司应该录取谁?解:(1)甲、乙各自成绩分别为90.8,91.9,录取乙;
(2)甲、乙各自成绩分别为92.5,92.15,录取甲.第33课时 统计初步拔高题
8.(2014年江苏徐州)(利用统计结果作出选择)甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9 乙:5,9,7,10,9
(1)填写下表:
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).解:(1)甲的众数为8,乙的平均数= (5+9+7+10+9)=8,乙的中位数为9;
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
故答案为:8,8,9;变小.第33课时 统计初步课时作业一、选择题
1.(2014?深圳)在﹣2,1,2,1,4,6中正确的是( )
A.平均数3 B.众数是﹣2 C.中位数是1 D.极差为8
2.(2013?深圳市)某校有21名同学们参加某比赛,预赛成绩各不同,要取前11名参加决赛,小颖已经知道了自己的成绩,她想知道自己能否进入决赛,只需要再知道这21名同学成绩的( )
A.最高分 B.中位数 C.极差 D.平均数
提示:21个数的中位数即为第11名的成绩,对比第11名即知自己是否被录取。DB第33课时 统计初步课时作业3. (2014年云南省)学校为了丰富学生课余活动开展了一次“爱我云南,唱我云南”的歌咏比赛,共有18名同学入围,他们的决赛成绩如下表:
则入围同学决赛成绩的中位数和众数分别是( )
A. 9.70,9.60 B.9.60,9.60
C.9.60,9.70 D.9.65,9.60
提示:∵共有18名同学,
则中位数为第9名和第10名同学成绩的平均分,
即中位数为: =9.60,
众数为:9.60.
4.(2014年广西钦州)体育课上,两名同学分别进行了5次立定跳远测试,要判断这5次测试中谁的成绩比较稳定,通常需要比较这两名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差DB第33课时 统计初步课时作业5. (2014?无锡)已知A样本的数据如下:72,73,76,76,77,78,78,78,B样本的数据恰好是A样本数据每个都加2,则A,B两个样本的下列统计量对应相同的是( )
A.平均数 B.标准差 C.中位数 D.众数B二、填空题
6.(2014年梅州)小明在射击训练中,五次命中的环数分别为5,7,6,6,6,则小明命中环数的众数为 ,平均数为 .
7.(2014?泉州)在综合实践课上,六名同学的作品数量(单位:件)分别为:3、5、2、5、5、7,则这组数据的众数为 件.
8. 在为灾区捐款中,各班的捐款数额如下(单位:元):99,101,103,97,102,96,104,95,105,100,则该校平均每班捐款为 .665100.2元第33课时 统计初步课时作业9. (2012?襄阳)在植树节当天,某校一个班同学分成10个小组参加植树造林活动,10个小组植树的株数见下表:则这10个小组植树株数的方差是 .
提示:根据表格得,平均数=(5×3+6×4+7×3)÷10=6
∴方差= 0.610. 某公司员工的月工资如下:580,650,880,900,1200,650,730,810
问:(1)公司所有员工的平均工资是 ;
(2)所有员工工资的中位数是 ;
(3)所有员工工资的众数是 ;
(4)用平均数还是中位数或是众数描述该公司员工工资的一般水平比较恰当,答 。800元770元650元中位数第33课时 统计初步课时作业三、解答题
11. (2014?珠海)某市体育中考共设跳绳、立定跳远、仰卧起坐三个项目,要求毎位学生必须且只需选考其中一项,该市东风中学初三(2)班学生选考三个项目的人数分布的条形统计图和扇形统计图如图所示.
(1)求该班的学生人数;
(2)若该校初三年级有1000人,估计该年级选考立定供远的人数.解:(1)根据题意得:30÷60%=50(人),则该校学生人数为50人;
(2)根据题意得:1000× =100(人),则估计该年级选考立定供远的人数为100人.第33课时 统计初步课时作业12.(2014年广东)某高校学生会发现同学们就餐时剩余饭菜较多,浪费严重,于是准备在校内倡导“光盘行动”,让同学们珍惜粮食,为了让同学们理解这次活动的重要性,校学生会在某天午餐后,随机调查了部分同学这餐饭菜的剩余情况,并将结果统计后绘制成了如1图和题2图所示的不完整的统计图。
(1)这次被调查的同学共有 名;
(2)把条形统计图补充完整;
(3)校学生会通过数据分析,估计这次被调
查的所有学生一餐浪费的食物可以供200人用
一餐.据此估算,该校18 000名学生一餐浪费
的食物可供多少人食用一餐?解:(1)1000名;
(2)剩少量饭菜的人数为:
1000-(400+250+150)200(人).
(3) ×18000=3600(人)
答:估计可供3600人食用一餐。1000第33课时 统计初步课时作业13. (2014?绍兴)为了解某校七,八年级学生的睡眠情况,随机抽取了该校七,八年级部分学生进行调查,已知抽取七年级与八年级的学生人数相同,利用抽样所得的数据绘制如下统计图表.
根据图表提供的信息,回答下列问题:
(1)求统计图中的a;
(2)抽取的样本中,八年级学生睡眠时间在C组的有多少人?
(3)已知该校七年级学生有755人,八年级学生有785人,如果睡眠时间x(时)满足:7.5≤x≤9.5,称睡眠时间合格,试估计该校七、八年级学生中睡眠时间合格的共有多少人?第33课时 统计初步课时作业解:(1)根据题意得:a=1﹣(35%+25%+25%+10%)=5%;
(2)根据题意得:(6+19+17+10+8)×35%=21(人),
则抽取的样本中,八年级学生睡眠时间在C组的有21人;
(3)根据题意得:755× +785×(25%+35%)=453+471=924(人)
则该校七、八年级学生中睡眠时间合格的共有924人.第33课时 统计初步课时作业14.(2014?泉州)课外阅读是提高学生素养的重要途径.某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时).根据t的长短分为A,B,C,D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
(1)求表格中的a的值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
解:(1)50﹣10﹣20﹣15=5(名),故a的值为5,条形统计图如下:
(2)1300× =520(名),答:估计该校共有520名学生课外阅读时间不少于1小时.50名学生平均每天课外阅读时间统计表结束谢谢!
同课章节目录
