广东省2015中考数学冲刺复习课件:第31课时 尺规作图(共22张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第31课时 尺规作图(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 745.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:06:30 | ||
图片预览







文档简介
课件22张PPT。数学
第31课时 尺规作图第31课时 尺规作图最新广东省初中毕业生数学学科学业考试大纲
【分类】尺规作图
【考点说明】
①完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线.
②利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形.
③了解如何过一点、两点和不在同一直线上的三点作圆.
④了解尺规作图的步骤(不要求作法).第31课时 尺规作图知识考点?对应精练
考点分类一 基本作图
【知识考点】
基本作图:(1)作一条线段等于已知线段;(2)作线段的垂直平分线;(3)作角的平分线;(4)作一个角等于已知角;(5)过一点作已知直线的垂线.
利用基本作图作特殊图形:(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边和高作等腰三角形;(5)作三角形的内切圆和外接圆.
【对应精练】
1. (2014山东青岛)已知:线段a,∠α.
求作:△ABC,使AB=AC=a,∠B=∠α.
解:如图所示:△ABC即为所求.第31课时 尺规作图考点分类二 作图与证明
【对应精练】
1.如图,△ABC中,∠C=90°,∠A=30°,
(1)用直尺和圆规,作AB边上的垂直平分线DE,交AC于点D,交AB于点E;(保留作图痕迹,不写作法)
(2)连接BD,求证:BD平分∠CBA.
解:(1)如图所示,DE就是要求作的AB边上的垂直平分线;
(2)证明:∵DE是AB边上的垂直平分线,∠A=30°.
∴AD=BD,∴∠ABD=∠A=30°.
∵∠C=90°,
∴∠ABC=90°-∠A=90°-30°=60°.
∴∠CBD=∠ABC-∠ABD=60°-30°=30°.
∴∠ABD=∠CBD
即BD平分∠CBA.第31课时 尺规作图2.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求。连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
B考点分类三 作图与应用
1.如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)解:如图所示:作CD的垂直平分线,∠AOB的角平分线的交点P即为所求.第31课时 尺规作图真题演练?层层推进
基础题
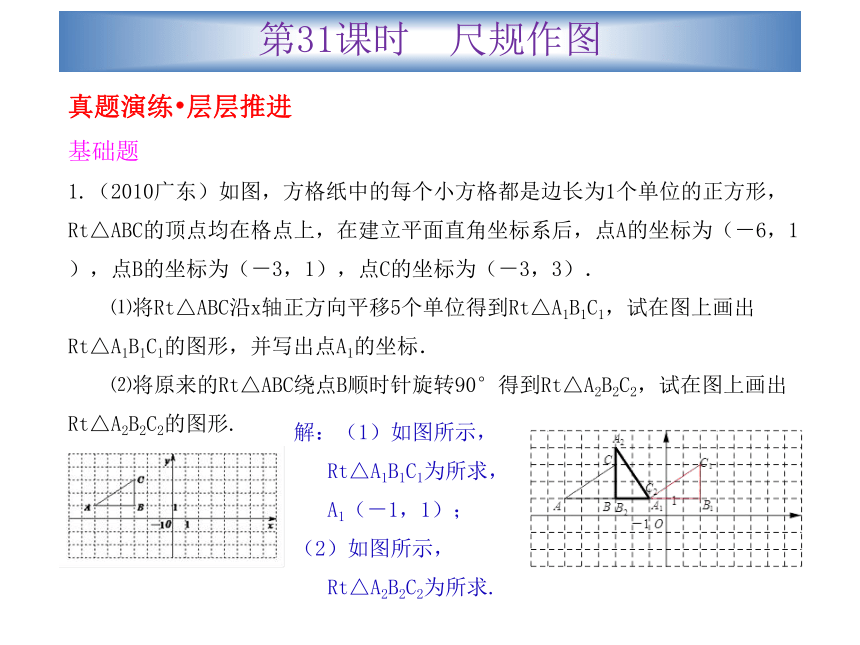
1.(2010广东)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
⑴将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形,并写出点A1的坐标.
⑵将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形.解:(1)如图所示,Rt△A1B1C1为所求, A1(-1,1);
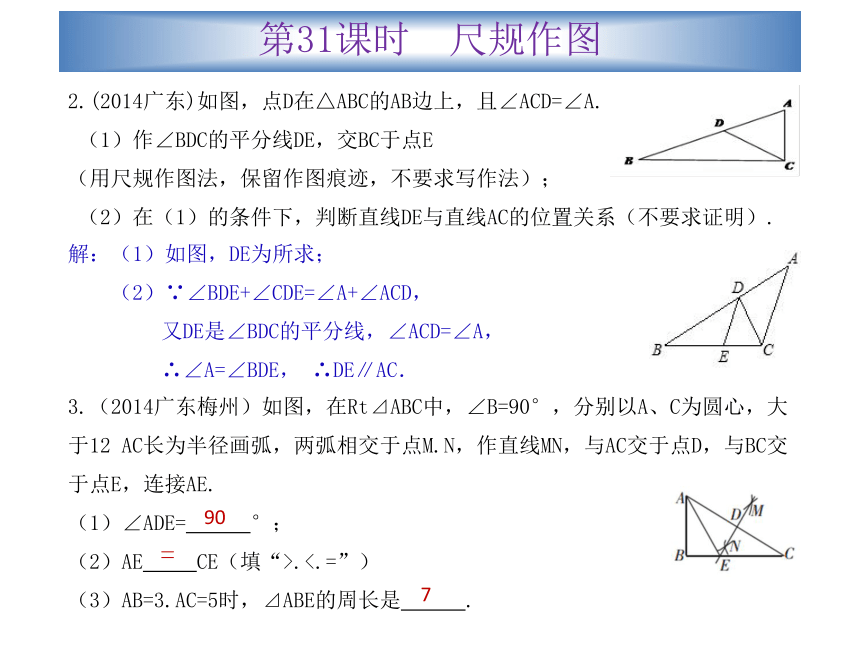
(2)如图所示,Rt△A2B2C2为所求.第31课时 尺规作图2.(2014广东)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E
(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明). 解:(1)如图,DE为所求;
(2)∵∠BDE+∠CDE=∠A+∠ACD,
又DE是∠BDC的平分线,∠ACD=∠A,
∴∠A=∠BDE, ∴DE∥AC.3.(2014广东梅州)如图,在Rt⊿ABC中,∠B=90°,分别以A、C为圆心,大于12 AC长为半径画弧,两弧相交于点M.N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
(1)∠ADE= °;
(2)AE CE(填“>.<.=”)
(3)AB=3.AC=5时,⊿ABE的周长是 .90=7第31课时 尺规作图4.(2012广东)如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.解:(1)如图所示;
(2)∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°﹣2∠ABC=180°﹣144°=36°,
∵AD是∠ABC的平分线,
∴∠ABD= ∠ABC= ×72°=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.第31课时 尺规作图提高题
5.(2014广东汕尾)如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于 AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
(1)求∠ADE;(直接写出结果)
(2)当AB=3,AC=5时,求△ABE的周长.解:(1)∵由题意可知MN是线段AC的垂直平分线,
∴∠ADE=90°;
(2)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC= =4,
∵MN是线段AC的垂直平分线,
∴AE=CE,
∴△ABE的周长=AB+(AE+BE)=AB+BC=3+4=7.第31课时 尺规作图6..(2013广东)如题19图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC
(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,不连结AE,交CD于点F,求证:△AFD≌△EFC. 解:(1)如图所示,线段CE为所求;
(2)证明:在□ABCD中,AD∥BC,AD=BC.
∴∠CEF=∠DAF
∵CE=BC,∴AD=CE,
又∵∠CFE=∠DFA,
∴△AFD≌△EFC.第31课时 尺规作图7.(2013广东广州)已知四边形ABCD是平行四边形,如图,把△ABD沿对角线BD翻折180°得到△A′BD.
(1)利用尺规作出A′BD.(要求保留作图痕迹,不写作法);
(2)设DA′与BC交于点E,求证:△DA′E≌△DCE.
解:(1)如图所示
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠C,
由折叠的性质可得:∠BA′D=∠BAD,A′B=AB,
∴∠BA′D=∠C,A′B=CD,
又∠BEA′=∠DEC,
∴△BA′E≌△DCE(AAS).第31课时 尺规作图拔高题
8.(1)观察发现
如图①:若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图②:在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 . 解:(1)观察发现如图②,CE的长为BP+PE的最小值,
∵在等边三角形ABC中,AB=2,点E是AB的中点;
∴CE⊥AB,BE=1,
∴CE= BE= ;
故答案为 .第31课时 尺规作图8.(2)实践运用
如图③:已知⊙O的直径CD为2, 的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .答案:(2)如图(3),过B点作弦BE⊥CD,连结AE交CD于P点,连结OB、OE、OA、PB,
∵BE⊥CD,
∴CD平分BE,即点E与点B关于CD对称,
∵AC 的度数为60°,点B是AC的中点,
∴∠BOC=30°,∠AOC=60°,
∴∠EOC=30°,
∴∠AOE=60°+30°=90°,
∵OA=OE=1,
∴AE=2OA=
∵AE的长就是BP+AP的最小值.
∴BP+AP= ;第31课时 尺规作图8. (3)拓展延伸
如图④:点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.答案:(3)如图.
做点P关于直线AB的对称点E,
做点P关于直线BC的对称点F,
连接EF分别交于AB,BC的M和N点。第31课时 尺规作图课时作业一、选择题
1.在下列各画法中,属于尺规作图的是( )
A.用三角板画30°的角 B.用直尺和三角板画平行线
C.用角尺画角的平分线
D.用圆规在已知直线上截取一条线段等于已知线段
2.下列作图语句正确的是( )
A.过A、B、C三点作直线 B.延长线段AB=α
C.以点O为圆心画弧 D.以线段AB为直径作半圆3.如图;点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为直径的弧
B.以点C为圆心,DM为直径的弧
C.以点E为圆心,OD为直径的弧
D.以点E为圆心,DM为直径的弧DDD第31课时 尺规作图课时作业4.用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A.SAS B.SSS C.ASA D.AAS5.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对BB第31课时 尺规作图课时作业二、填空题
6.在△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD. 若CD=AC,∠B=25°,则∠ACB的度数为 . 7.如图,在△ABC,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径,画弧,分别交AB, AC于点E、F;②分别以点E,F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边与点D,则∠ADC 的度数为 .平行四边形65°105°8.如图,点A上直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是 .第31课时 尺规作图课时作业9.如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 .三、解答题
10.已知:线段a,∠α.求作:△ABC,使AB=AC=a,∠B=∠α.
解:如图所示:△ABC即为所求.90°第31课时 尺规作图课时作业11.已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE。解:(1) 如图,点D、E为所求;
证:(2) ∵BD平分∠ABC,∠B=60°,
∴∠ABD= ∠ABC=30°,
又∠A=30°,
∴∠ABD=∠A,
又∵∠AED=∠BED=90°,DE=DE,
∴△ADE≌△BDE.第31课时 尺规作图课时作业12.如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.解:(1) 如图所示,BD为所求;
(2) ∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°-2∠ABC=180°-144°=36°,
∵AD是∠ABC的平分线,
∴∠ABD= ∠ABC=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.第31课时 尺规作图课时作业13. 如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于 AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1) 求证:△AED≌△CFD;
(2) 求证:四边形AECF是菱形.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB, ∴∠EAC=∠FCA,∠CFD=∠AED,
又AD=CD, ∴△AED≌△CFD;
(2)∵△AED≌△CFD, ∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA, ∴EC=EA=FC=FA,
∴四边形AECF为菱形.结束谢谢!
【分类】尺规作图
【考点说明】
①完成以下基本作图:作一条线段等于已知线段,作一个角等于已知角,作角的平分线,作线段的垂直平分线.
②利用基本作图作三角形:已知三边作三角形;已知两边及其夹角作三角形;已知两角及其夹边作三角形;已知底边及底边上的高作等腰三角形.
③了解如何过一点、两点和不在同一直线上的三点作圆.
④了解尺规作图的步骤(不要求作法).第31课时 尺规作图知识考点?对应精练
考点分类一 基本作图
【知识考点】
基本作图:(1)作一条线段等于已知线段;(2)作线段的垂直平分线;(3)作角的平分线;(4)作一个角等于已知角;(5)过一点作已知直线的垂线.
利用基本作图作特殊图形:(1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边和高作等腰三角形;(5)作三角形的内切圆和外接圆.
【对应精练】
1. (2014山东青岛)已知:线段a,∠α.
求作:△ABC,使AB=AC=a,∠B=∠α.
解:如图所示:△ABC即为所求.第31课时 尺规作图考点分类二 作图与证明
【对应精练】
1.如图,△ABC中,∠C=90°,∠A=30°,
(1)用直尺和圆规,作AB边上的垂直平分线DE,交AC于点D,交AB于点E;(保留作图痕迹,不写作法)
(2)连接BD,求证:BD平分∠CBA.
解:(1)如图所示,DE就是要求作的AB边上的垂直平分线;
(2)证明:∵DE是AB边上的垂直平分线,∠A=30°.
∴AD=BD,∴∠ABD=∠A=30°.
∵∠C=90°,
∴∠ABC=90°-∠A=90°-30°=60°.
∴∠CBD=∠ABC-∠ABD=60°-30°=30°.
∴∠ABD=∠CBD
即BD平分∠CBA.第31课时 尺规作图2.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求。连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形
B考点分类三 作图与应用
1.如图,两条公路OA和OB相交于O点,在∠AOB的内部有工厂C和D,现要修建一个货站P,使货站P到两条公路OA、OB的距离相等,且到两工厂C、D的距离相等,用尺规作出货站P的位置.(要求:不写作法,保留作图痕迹,写出结论)解:如图所示:作CD的垂直平分线,∠AOB的角平分线的交点P即为所求.第31课时 尺规作图真题演练?层层推进
基础题
1.(2010广东)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
⑴将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形,并写出点A1的坐标.
⑵将原来的Rt△ABC绕点B顺时针旋转90°得到Rt△A2B2C2,试在图上画出Rt△A2B2C2的图形.解:(1)如图所示,Rt△A1B1C1为所求, A1(-1,1);
(2)如图所示,Rt△A2B2C2为所求.第31课时 尺规作图2.(2014广东)如图,点D在△ABC的AB边上,且∠ACD=∠A.
(1)作∠BDC的平分线DE,交BC于点E
(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,判断直线DE与直线AC的位置关系(不要求证明). 解:(1)如图,DE为所求;
(2)∵∠BDE+∠CDE=∠A+∠ACD,
又DE是∠BDC的平分线,∠ACD=∠A,
∴∠A=∠BDE, ∴DE∥AC.3.(2014广东梅州)如图,在Rt⊿ABC中,∠B=90°,分别以A、C为圆心,大于12 AC长为半径画弧,两弧相交于点M.N,作直线MN,与AC交于点D,与BC交于点E,连接AE.
(1)∠ADE= °;
(2)AE CE(填“>.<.=”)
(3)AB=3.AC=5时,⊿ABE的周长是 .90=7第31课时 尺规作图4.(2012广东)如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.解:(1)如图所示;
(2)∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°﹣2∠ABC=180°﹣144°=36°,
∵AD是∠ABC的平分线,
∴∠ABD= ∠ABC= ×72°=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.第31课时 尺规作图提高题
5.(2014广东汕尾)如图,在Rt△ABC中,∠B=90°,分别以点A、C为圆心,大于 AC长为半径画弧,两弧相交于点M、N,连接MN,与AC、BC分别交于点D、E,连接AE.
(1)求∠ADE;(直接写出结果)
(2)当AB=3,AC=5时,求△ABE的周长.解:(1)∵由题意可知MN是线段AC的垂直平分线,
∴∠ADE=90°;
(2)∵在Rt△ABC中,∠B=90°,AB=3,AC=5,
∴BC= =4,
∵MN是线段AC的垂直平分线,
∴AE=CE,
∴△ABE的周长=AB+(AE+BE)=AB+BC=3+4=7.第31课时 尺规作图6..(2013广东)如题19图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC
(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,不连结AE,交CD于点F,求证:△AFD≌△EFC. 解:(1)如图所示,线段CE为所求;
(2)证明:在□ABCD中,AD∥BC,AD=BC.
∴∠CEF=∠DAF
∵CE=BC,∴AD=CE,
又∵∠CFE=∠DFA,
∴△AFD≌△EFC.第31课时 尺规作图7.(2013广东广州)已知四边形ABCD是平行四边形,如图,把△ABD沿对角线BD翻折180°得到△A′BD.
(1)利用尺规作出A′BD.(要求保留作图痕迹,不写作法);
(2)设DA′与BC交于点E,求证:△DA′E≌△DCE.
解:(1)如图所示
(2)∵四边形ABCD是平行四边形,
∴AB=CD,∠BAD=∠C,
由折叠的性质可得:∠BA′D=∠BAD,A′B=AB,
∴∠BA′D=∠C,A′B=CD,
又∠BEA′=∠DEC,
∴△BA′E≌△DCE(AAS).第31课时 尺规作图拔高题
8.(1)观察发现
如图①:若点A、B在直线m同侧,在直线m上找一点P,使AP+BP的值最小,做法如下:
作点B关于直线m的对称点B′,连接AB′,与直线m的交点就是所求的点P,线段AB′的长度即为AP+BP的最小值.
如图②:在等边三角形ABC中,AB=2,点E是AB的中点,AD是高,在AD上找一点P,使BP+PE的值最小,做法如下:
作点B关于AD的对称点,恰好与点C重合,连接CE交AD于一点,则这点就是所求的点P,故BP+PE的最小值为 . 解:(1)观察发现如图②,CE的长为BP+PE的最小值,
∵在等边三角形ABC中,AB=2,点E是AB的中点;
∴CE⊥AB,BE=1,
∴CE= BE= ;
故答案为 .第31课时 尺规作图8.(2)实践运用
如图③:已知⊙O的直径CD为2, 的度数为60°,点B是 的中点,在直径CD上作出点P,使BP+AP的值最小,则BP+AP的值最小,则BP+AP的最小值为 .答案:(2)如图(3),过B点作弦BE⊥CD,连结AE交CD于P点,连结OB、OE、OA、PB,
∵BE⊥CD,
∴CD平分BE,即点E与点B关于CD对称,
∵AC 的度数为60°,点B是AC的中点,
∴∠BOC=30°,∠AOC=60°,
∴∠EOC=30°,
∴∠AOE=60°+30°=90°,
∵OA=OE=1,
∴AE=2OA=
∵AE的长就是BP+AP的最小值.
∴BP+AP= ;第31课时 尺规作图8. (3)拓展延伸
如图④:点P是四边形ABCD内一点,分别在边AB、BC上作出点M,点N,使PM+PN的值最小,保留作图痕迹,不写作法.答案:(3)如图.
做点P关于直线AB的对称点E,
做点P关于直线BC的对称点F,
连接EF分别交于AB,BC的M和N点。第31课时 尺规作图课时作业一、选择题
1.在下列各画法中,属于尺规作图的是( )
A.用三角板画30°的角 B.用直尺和三角板画平行线
C.用角尺画角的平分线
D.用圆规在已知直线上截取一条线段等于已知线段
2.下列作图语句正确的是( )
A.过A、B、C三点作直线 B.延长线段AB=α
C.以点O为圆心画弧 D.以线段AB为直径作半圆3.如图;点C在∠AOB的边OB上,用尺规作出了CN∥OA,作图痕迹中,弧FG是( )
A.以点C为圆心,OD为直径的弧
B.以点C为圆心,DM为直径的弧
C.以点E为圆心,OD为直径的弧
D.以点E为圆心,DM为直径的弧DDD第31课时 尺规作图课时作业4.用直尺和圆规作一个角等于已知角,如图,能得出∠A'O'B'=∠AOB的依据是( )
A.SAS B.SSS C.ASA D.AAS5.如图,小红在作线段AB的垂直平分线时,是这样操作的:分别以点A,B为圆心,大于线段AB长度一半的长为半径画弧,相交于点C,D,则直线CD即为所求.连结AC,BC,AD,BD,根据她的作图方法可知,四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.以上都不对BB第31课时 尺规作图课时作业二、填空题
6.在△ABC中,按以下步骤作图:①分别以B、C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M、N;②作直线MN交AB于点D,连接CD. 若CD=AC,∠B=25°,则∠ACB的度数为 . 7.如图,在△ABC,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC的长为半径,画弧,分别交AB, AC于点E、F;②分别以点E,F为圆心,大于 EF的长为半径画弧,两弧相交于点G;③作射线AG,交BC边与点D,则∠ADC 的度数为 .平行四边形65°105°8.如图,点A上直线l外一点,在l上取两点B、C,分别以A、C为圆心,BC、AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是 .第31课时 尺规作图课时作业9.如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法,注意最后用墨水笔加黑),并直接写出旋转角度是 .三、解答题
10.已知:线段a,∠α.求作:△ABC,使AB=AC=a,∠B=∠α.
解:如图所示:△ABC即为所求.90°第31课时 尺规作图课时作业11.已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD,交AC于点D;作AB的中点E(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE。解:(1) 如图,点D、E为所求;
证:(2) ∵BD平分∠ABC,∠B=60°,
∴∠ABD= ∠ABC=30°,
又∠A=30°,
∴∠ABD=∠A,
又∵∠AED=∠BED=90°,DE=DE,
∴△ADE≌△BDE.第31课时 尺规作图课时作业12.如图,在△ABC中,AB=AC,∠ABC=72°.
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.解:(1) 如图所示,BD为所求;
(2) ∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°-2∠ABC=180°-144°=36°,
∵AD是∠ABC的平分线,
∴∠ABD= ∠ABC=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.第31课时 尺规作图课时作业13. 如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于 AC的长为半径画弧,两弧交于P,Q两点;
②作直线PQ,分别交AB,AC于点E,D,连接CE;
③过C作CF∥AB交PQ于点F,连接AF.
(1) 求证:△AED≌△CFD;
(2) 求证:四边形AECF是菱形.解:(1)由作图知:PQ为线段AC的垂直平分线,
∴AE=CE,AD=CD,
∵CF∥AB, ∴∠EAC=∠FCA,∠CFD=∠AED,
又AD=CD, ∴△AED≌△CFD;
(2)∵△AED≌△CFD, ∴AE=CF,
∵EF为线段AC的垂直平分线,
∴EC=EA,FC=FA, ∴EC=EA=FC=FA,
∴四边形AECF为菱形.结束谢谢!
同课章节目录
