广东省2015中考数学冲刺复习课件:第30课时 轴对称与中心对称(共19张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第30课时 轴对称与中心对称(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 702.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:07:17 | ||
图片预览






文档简介
课件19张PPT。数学
第30课时 轴对称与中心对称第30课时 轴对称与中心对称最新广东省初中毕业生数学学科学业考试大纲
【分类】图形的轴对称.
【考点说明】
①通过具体实例认识轴对称,理解对应点所连的线段被对称轴垂直平分的性质
②认识并欣赏自然界和现实生活中的轴对称图形.
知识考点?对应精练
考点分类一 轴对称
【知识考点】
轴对称图形的概念:如果一个图形沿着一条直线对称,对折两部分是完全重合的,那么就称这样的图形为轴对称图形.
轴对称的概念:把一个图形沿着一条直线翻折180°后,如果它能与另一个图形重合,那么这称这两个图形关于这条直线轴对称,这条直线叫做对称轴.
轴对称的性质:(1)两个图形全等,对应线段相等,对应角相等;
(2)对称点的连线被对称轴垂直平分.第30课时 轴对称与中心对称【对应精练】
1. (2014山东泰安)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
(A)1 (B)2 (C)3 (D)4
【解析】四个图形都是轴对称图形,其中(A)(B)(C)有2条对称轴,而(D)有3条对称轴.C第30课时 轴对称与中心对称2.(2014黑龙江牡丹江)已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°【解析】∵在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,
∴AM=MC=BM, ∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵∠A+∠B=∠B+∠BCD=90°
∴∠A=∠BCD
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.A第30课时 轴对称与中心对称考点分类二 中心对称
【知识考点】
中心对称的概念:把一个图形沿着某一点旋转180°后,如果它能与另一个图形重合,那么这两个图形成中心对称,这个点叫做对称中心.
中心对称的性质:(1)两个图形全等,对应线段相等,对应角相等;
(2)对称点的连线经过对称中心,且被对称中心平分.
【对应精练】
1.(2014山东潍坊)下列标志中不是中心对称图形的是( ).
中国移动 中国银行 中国人民银行 方正集团
A. B. C. D.
【解析】根据中心对称图形可知,旋转180度后与自身完全重合;而轴对称图形是沿某条直线对折后,可知图形两边的部分能完全重合.所以选项A、B、D三个图形是中心对称图形,而选项C的图形是轴对称图形。C第30课时 轴对称与中心对称考点分类三 图形对称的综合运用
【对应精练】
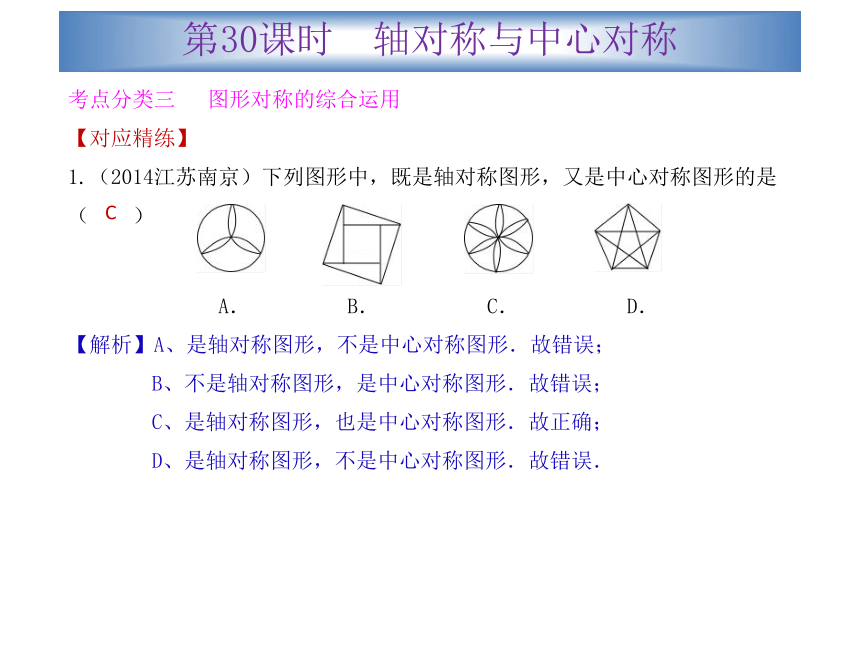
1.(2014江苏南京)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解析】A、是轴对称图形,不是中心对称图形.故错误;
B、不是轴对称图形,是中心对称图形.故错误;
C、是轴对称图形,也是中心对称图形.故正确;
D、是轴对称图形,不是中心对称图形.故错误.C第30课时 轴对称与中心对称2.(2014黑龙江龙东) 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 。
【解析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.53.(2014湖北荆门)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
【解析】利用轴对称图形的性质以及中心对称图形的性质分析得出符合题意的图形即可.如图所示:组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.C第30课时 轴对称与中心对称真题演练?层层推进
基础题
1.(2013广东)下列图形中,不是轴对称图形的是( )
2.(2014广东汕尾)下列电视台的台标,是中心对称图形的是( )
A. B. C. D.
3.(2014广东深圳)下列图形中是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
CAB第30课时 轴对称与中心对称4.(2014广东)在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
5.(2012广东汕头)下列平面图形,既是中心对称图形,又是轴对称图形的是( )
A.等腰三角形 B.正五边形 C.平行四边形 D.矩形CDA提高题
6.(2013广东湛江)四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片是轴对称图形的概率是( )
A. B. C. D.1第30课时 轴对称与中心对称7.(2011广东)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.解:(1)∵BF=CF=8, ∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°;
(2)∵∠EBC=60°, ∴∠ADB=60°,
∵BF=CF=8. ∴BD=BF?sin60°=
∴在Rt△BAD中, AB=BD×sin60°=6.第30课时 轴对称与中心对称拔高题
8.(2012广东)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.【答案】(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,∴∠ABG=∠ADE。
在△ABG≌△C′DG中,∵∠BAG=∠C,AB= C′D,∠ABG=∠AD C′,
∴△ABG≌△C′DG(ASA)。【解析】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论。第30课时 轴对称与中心对称【答案】(2)解:∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8﹣x,
在Rt△ABG中,∵AB2+AG2=BG2,即62+x2=(8﹣x)2,
解得x= ,
∴tan∠ABG= ;
【解析】(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,从而得出tan∠ABG的值。第30课时 轴对称与中心对称【答案】(3)解:∵△AEF是△DEF翻折而成,
∴EF垂直平分AD。
∴HD= AD=4。
∵tan∠ABG=tan∠ADE= ,
∴EH=HD× =4× = ,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF= AB= ×6=3,
∴EF=EH+HF= +3= .
【解析】(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD= AD=4,再根据tan∠ABG的值即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结果.第30课时 轴对称与中心对称课时作业一、选择题
1.点P(-1,2)关于y轴对称的点的坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
2.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
3.下列标志中不是中心对称图形的是( ).
中国移动 中国银行 中国人民银行 方正集团
A. B. C. D.
4.下列图形是中心对称图形,但不是轴对称图形的是( )
A.平行四边形 B.等边三角形 C.圆 D.正方形ACCA第30课时 轴对称与中心对称课时作业5.下列四种图形都是轴对称图形,其中对称轴条数最多的图形是( )
A.等边三角形 B.矩形 C.菱形 D.正方形
二、填空题
6.下列图形:①平行四边形; ②菱形; ③圆; ④等腰三角形; ⑤直角三角形; ⑥国旗上的五角星。这些图形中既是轴对称图形又是中心对称图形的是 .(填写序号)
7.等边三角形边长为4 cm,则其面积为___________cm2.D②③208.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= .9.在四边形ABCD中,AB=CD,要使四边形ABCD是中心对称图形,只需添加一个条件,这个条件可以是 .(只要填写一种情况)
10.如图,已知△ABC中,AB=AC=26,DE是AB的垂直平分线,交AB于点E,交AC于点D,且△BDC的周长为46,则BC=__________.AB//CD或AD=BC,∠B+∠C=180o,∠A+∠D=180o等(不唯一)15 °第30课时 轴对称与中心对称课时作业三、解答题
11.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,求BC的长.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD, ∴BD+CD=12cm.12.如图,已知P是线段CD的垂直平分线上一点,PC⊥OA,PD⊥O,垂足为C、D.
求证: (1)OC=OD; (2)OP平分∠AOB.证明:(1)∵P在CD的垂直平分线上, ∴PC=PD.
又∵OP=OP, ∴Rt△OPC≌Rt△OPD(HL). ∴OC=OD.
(2)由(1)Rt△OPC≌△OPD知:∠AOP=∠BOP.
∴OP平分∠AOB.第30课时 轴对称与中心对称课时作业13.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.解:设BN=x,则依据折叠原理可得DN=AN=9-x,
∵D为BC的中点,
∴BN=3,
在Rt△ABC中,由勾股定理,得BN2+BD2=DN2,
∴32+x2=(9-x)2,
解得x=4,
∴BN=4.第30课时 轴对称与中心对称课时作业14.如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,求∠A的度数.解:∵在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,
∴AM=MC=BM,
∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵∠A+∠B=∠B+∠BCD=90°
∴∠A=∠BCD
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.结束谢谢!
【分类】图形的轴对称.
【考点说明】
①通过具体实例认识轴对称,理解对应点所连的线段被对称轴垂直平分的性质
②认识并欣赏自然界和现实生活中的轴对称图形.
知识考点?对应精练
考点分类一 轴对称
【知识考点】
轴对称图形的概念:如果一个图形沿着一条直线对称,对折两部分是完全重合的,那么就称这样的图形为轴对称图形.
轴对称的概念:把一个图形沿着一条直线翻折180°后,如果它能与另一个图形重合,那么这称这两个图形关于这条直线轴对称,这条直线叫做对称轴.
轴对称的性质:(1)两个图形全等,对应线段相等,对应角相等;
(2)对称点的连线被对称轴垂直平分.第30课时 轴对称与中心对称【对应精练】
1. (2014山东泰安)下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
(A)1 (B)2 (C)3 (D)4
【解析】四个图形都是轴对称图形,其中(A)(B)(C)有2条对称轴,而(D)有3条对称轴.C第30课时 轴对称与中心对称2.(2014黑龙江牡丹江)已知:如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,那么∠A的度数是( )
A.30° B.40° C.50° D.60°【解析】∵在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,
∴AM=MC=BM, ∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵∠A+∠B=∠B+∠BCD=90°
∴∠A=∠BCD
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.A第30课时 轴对称与中心对称考点分类二 中心对称
【知识考点】
中心对称的概念:把一个图形沿着某一点旋转180°后,如果它能与另一个图形重合,那么这两个图形成中心对称,这个点叫做对称中心.
中心对称的性质:(1)两个图形全等,对应线段相等,对应角相等;
(2)对称点的连线经过对称中心,且被对称中心平分.
【对应精练】
1.(2014山东潍坊)下列标志中不是中心对称图形的是( ).
中国移动 中国银行 中国人民银行 方正集团
A. B. C. D.
【解析】根据中心对称图形可知,旋转180度后与自身完全重合;而轴对称图形是沿某条直线对折后,可知图形两边的部分能完全重合.所以选项A、B、D三个图形是中心对称图形,而选项C的图形是轴对称图形。C第30课时 轴对称与中心对称考点分类三 图形对称的综合运用
【对应精练】
1.(2014江苏南京)下列图形中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.
【解析】A、是轴对称图形,不是中心对称图形.故错误;
B、不是轴对称图形,是中心对称图形.故错误;
C、是轴对称图形,也是中心对称图形.故正确;
D、是轴对称图形,不是中心对称图形.故错误.C第30课时 轴对称与中心对称2.(2014黑龙江龙东) 如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD的中点,P是线段BD上的一个动点,则PM+PN的最小值是 。
【解析】作M关于BD的对称点Q,连接NQ,交BD于P,连接MP,此时MP+NP的值最小,连接AC,求出CP、PB,根据勾股定理求出BC长,证出MP+NP=QN=BC,即可得出答案.53.(2014湖北荆门)如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有( )
A.2种 B.3种 C.4种 D.5种
【解析】利用轴对称图形的性质以及中心对称图形的性质分析得出符合题意的图形即可.如图所示:组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有4种.C第30课时 轴对称与中心对称真题演练?层层推进
基础题
1.(2013广东)下列图形中,不是轴对称图形的是( )
2.(2014广东汕尾)下列电视台的台标,是中心对称图形的是( )
A. B. C. D.
3.(2014广东深圳)下列图形中是轴对称图形但不是中心对称图形的是( )
A. B. C. D.
CAB第30课时 轴对称与中心对称4.(2014广东)在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
5.(2012广东汕头)下列平面图形,既是中心对称图形,又是轴对称图形的是( )
A.等腰三角形 B.正五边形 C.平行四边形 D.矩形CDA提高题
6.(2013广东湛江)四张质地、大小相同的卡片上,分别画上如下图所示的四个图形,在看不到图形的情况下从中任意抽出一张,则抽出的卡片是轴对称图形的概率是( )
A. B. C. D.1第30课时 轴对称与中心对称7.(2011广东)如图,直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,折叠纸片使BC经过点D,点C落在点E处,BF是折痕,且BF=CF=8.
(1)求∠BDF的度数;
(2)求AB的长.解:(1)∵BF=CF=8, ∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°;
(2)∵∠EBC=60°, ∴∠ADB=60°,
∵BF=CF=8. ∴BD=BF?sin60°=
∴在Rt△BAD中, AB=BD×sin60°=6.第30课时 轴对称与中心对称拔高题
8.(2012广东)如图,在矩形纸片ABCD中,AB=6,BC=8.把△BCD沿对角线BD折叠,使点C落在C′处,BC′交AD于点G;E、F分别是C′D和BD上的点,线段EF交AD于点H,把△FDE沿EF折叠,使点D落在D′处,点D′恰好与点A重合.
(1)求证:△ABG≌△C′DG;
(2)求tan∠ABG的值;
(3)求EF的长.【答案】(1)证明:∵△BDC′由△BDC翻折而成,
∴∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,∴∠ABG=∠ADE。
在△ABG≌△C′DG中,∵∠BAG=∠C,AB= C′D,∠ABG=∠AD C′,
∴△ABG≌△C′DG(ASA)。【解析】(1)根据翻折变换的性质可知∠C=∠BAG=90°,C′D=AB=CD,∠AGB=∠DGC′,故可得出结论。第30课时 轴对称与中心对称【答案】(2)解:∵由(1)可知△ABG≌△C′DG,
∴GD=GB,
∴AG+GB=AD,
设AG=x,则GB=8﹣x,
在Rt△ABG中,∵AB2+AG2=BG2,即62+x2=(8﹣x)2,
解得x= ,
∴tan∠ABG= ;
【解析】(2)由(1)可知GD=GB,故AG+GB=AD,设AG=x,则GB=8-x,在Rt△ABG中利用勾股定理即可求出AG的长,从而得出tan∠ABG的值。第30课时 轴对称与中心对称【答案】(3)解:∵△AEF是△DEF翻折而成,
∴EF垂直平分AD。
∴HD= AD=4。
∵tan∠ABG=tan∠ADE= ,
∴EH=HD× =4× = ,
∵EF垂直平分AD,AB⊥AD,
∴HF是△ABD的中位线,
∴HF= AB= ×6=3,
∴EF=EH+HF= +3= .
【解析】(3)由△AEF是△DEF翻折而成可知EF垂直平分AD,故HD= AD=4,再根据tan∠ABG的值即可得出EH的长,同理可得HF是△ABD的中位线,故可得出HF的长,由EF=EH+HF即可得出结果.第30课时 轴对称与中心对称课时作业一、选择题
1.点P(-1,2)关于y轴对称的点的坐标是( )
A.(1,2) B.(-1,2) C.(1,-2) D.(-1,-2)
2.下列四个图形:
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A.1 B.2 C.3 D.4
3.下列标志中不是中心对称图形的是( ).
中国移动 中国银行 中国人民银行 方正集团
A. B. C. D.
4.下列图形是中心对称图形,但不是轴对称图形的是( )
A.平行四边形 B.等边三角形 C.圆 D.正方形ACCA第30课时 轴对称与中心对称课时作业5.下列四种图形都是轴对称图形,其中对称轴条数最多的图形是( )
A.等边三角形 B.矩形 C.菱形 D.正方形
二、填空题
6.下列图形:①平行四边形; ②菱形; ③圆; ④等腰三角形; ⑤直角三角形; ⑥国旗上的五角星。这些图形中既是轴对称图形又是中心对称图形的是 .(填写序号)
7.等边三角形边长为4 cm,则其面积为___________cm2.D②③208.如图,在等腰三角形纸片ABC中,AB=AC,∠A=50°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= .9.在四边形ABCD中,AB=CD,要使四边形ABCD是中心对称图形,只需添加一个条件,这个条件可以是 .(只要填写一种情况)
10.如图,已知△ABC中,AB=AC=26,DE是AB的垂直平分线,交AB于点E,交AC于点D,且△BDC的周长为46,则BC=__________.AB//CD或AD=BC,∠B+∠C=180o,∠A+∠D=180o等(不唯一)15 °第30课时 轴对称与中心对称课时作业三、解答题
11.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,求BC的长.解:根据折叠可得:AD=BD,
∵△ADC的周长为17cm,AC=5cm,
∴AD+DC=17﹣5=12(cm),
∵AD=BD, ∴BD+CD=12cm.12.如图,已知P是线段CD的垂直平分线上一点,PC⊥OA,PD⊥O,垂足为C、D.
求证: (1)OC=OD; (2)OP平分∠AOB.证明:(1)∵P在CD的垂直平分线上, ∴PC=PD.
又∵OP=OP, ∴Rt△OPC≌Rt△OPD(HL). ∴OC=OD.
(2)由(1)Rt△OPC≌△OPD知:∠AOP=∠BOP.
∴OP平分∠AOB.第30课时 轴对称与中心对称课时作业13.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,求线段BN的长.解:设BN=x,则依据折叠原理可得DN=AN=9-x,
∵D为BC的中点,
∴BN=3,
在Rt△ABC中,由勾股定理,得BN2+BD2=DN2,
∴32+x2=(9-x)2,
解得x=4,
∴BN=4.第30课时 轴对称与中心对称课时作业14.如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,CM是斜边AB上的中线,将△ACM沿直线CM折叠,点A落在点D处,如果CD恰好与AB垂直,求∠A的度数.解:∵在Rt△ABC中,∠ACB=90°,CM是斜边AB上的中线,
∴AM=MC=BM,
∴∠A=∠MCA,
∵将△ACM沿直线CM折叠,点A落在点D处,
∴CM平分∠ACD,∠A=∠D,
∴∠ACM=∠MCD,
∵∠A+∠B=∠B+∠BCD=90°
∴∠A=∠BCD
∴∠BCD=∠DCM=∠MCA=30°
∴∠A=30°.结束谢谢!
同课章节目录
