广东省2015中考数学冲刺复习课件:第29课时 平移与旋转(共16张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第29课时 平移与旋转(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 599.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 00:00:00 | ||
图片预览



文档简介
课件16张PPT。数学
第29课时 平移与旋转第29课时 平移与旋转知识考点?对应精练
考点分类一 图形的平移
【知识考点】
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变换,叫做平移变换,简称平移,平移前后互相重合的点叫做对应点.
平移的性质:(1)对应线段平行(或共线) 相等,对应点所连的线段平行(或共线)且相等,图形上的点都沿同一方向移动了相同的距离;
(2)对应角相等;(3)平移前后的两个图形是全等图形.
【对应精练】1.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF ,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12C152.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .第29课时 平移与旋转考点分类二 图形的旋转
【知识考点】
旋转的概念:在平面内,把一个图形绕着一个定点着某个方向旋转一定的角度,图形的这种变换,叫做旋转变换,其中这个定点叫做旋转中心,这个角度叫做旋转角,旋转前后的点叫做对应点.
旋转的性质:
(1)图形上的每一点都绕着旋转中心,沿着相同的方向旋转同样的大小的角度;
(2)旋转后的图形与原来的图形的形状和大小都没有发生变化,即它们是全等的;
(3)旋转前后两个图形的对应点到旋转中心的距离相等;
(4)对应点到旋转中心的连线所成的角相等,并且等于旋转角.第29课时 平移与旋转【对应精练】
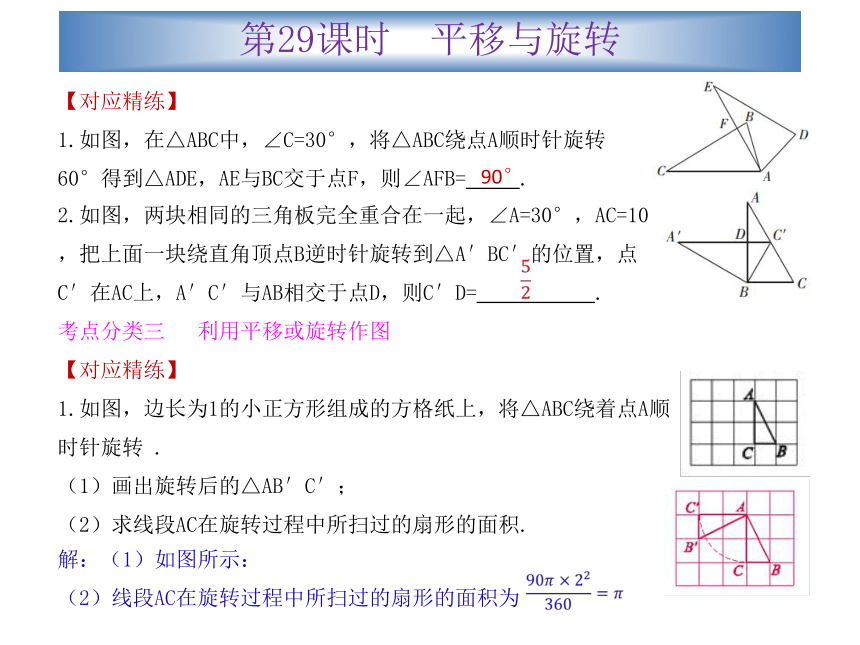
1.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于点F,则∠AFB= .2.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D= .90°考点分类三 利用平移或旋转作图
【对应精练】
1.如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转 .
(1)画出旋转后的△AB′C′;
(2)求线段AC在旋转过程中所扫过的扇形的面积.解:(1)如图所示:
(2)线段AC在旋转过程中所扫过的扇形的面积为? ?第29课时 平移与旋转真题演练?层层推进
基础题
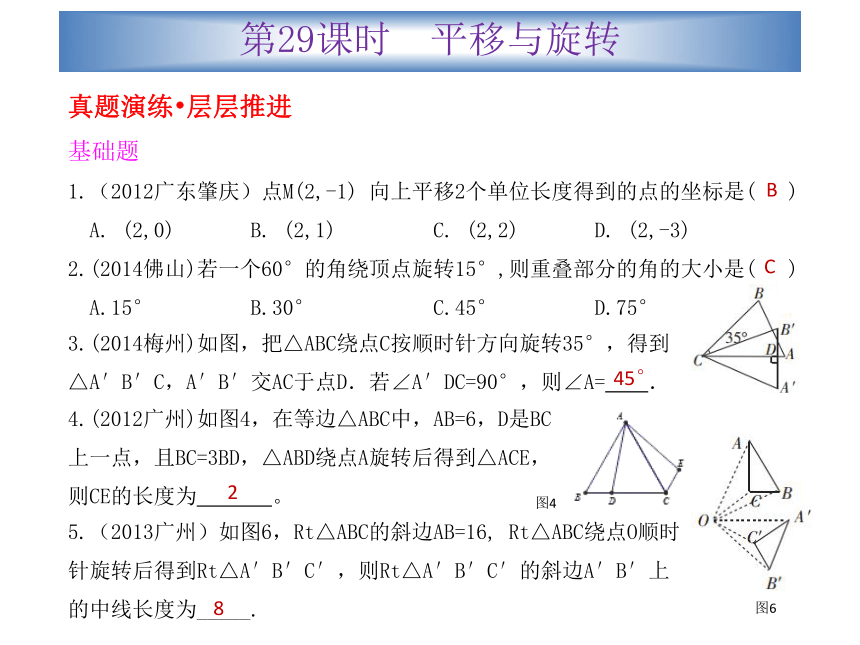
1.(2012广东肇庆)点M(2,-1) 向上平移2个单位长度得到的点的坐标是( )
A. (2,0) B. (2,1) C. (2,2) D. (2,-3)
2.(2014佛山)若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°3.(2014梅州)如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= .4.(2012广州)如图4,在等边△ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 。5.(2013广州)如图6,Rt△ABC的斜边AB=16, Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′,则Rt△A′B′C′的斜边A′B′上的中线长度为_____.图4图6BC2845°第29课时 平移与旋转提高题
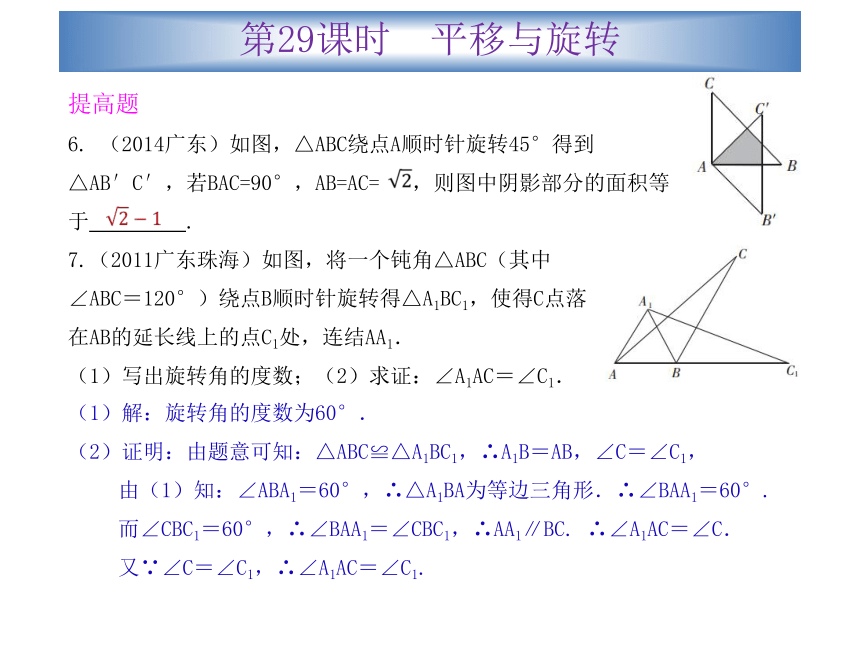
6. (2014广东)如图,△ABC绕点A顺时针旋转45°得到△AB′C′,若BAC=90°,AB=AC= ,则图中阴影部分的面积等于 .7.(2011广东珠海)如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;(2)求证:∠A1AC=∠C1.(1)解:旋转角的度数为60°.
(2)证明:由题意可知:△ABC≌△A1BC1,∴A1B=AB,∠C=∠C1,
由(1)知:∠ABA1=60°,∴△A1BA为等边三角形.∴∠BAA1=60°.
而∠CBC1=60°,∴∠BAA1=∠CBC1,∴AA1∥BC. ∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.第29课时 平移与旋转拔高题
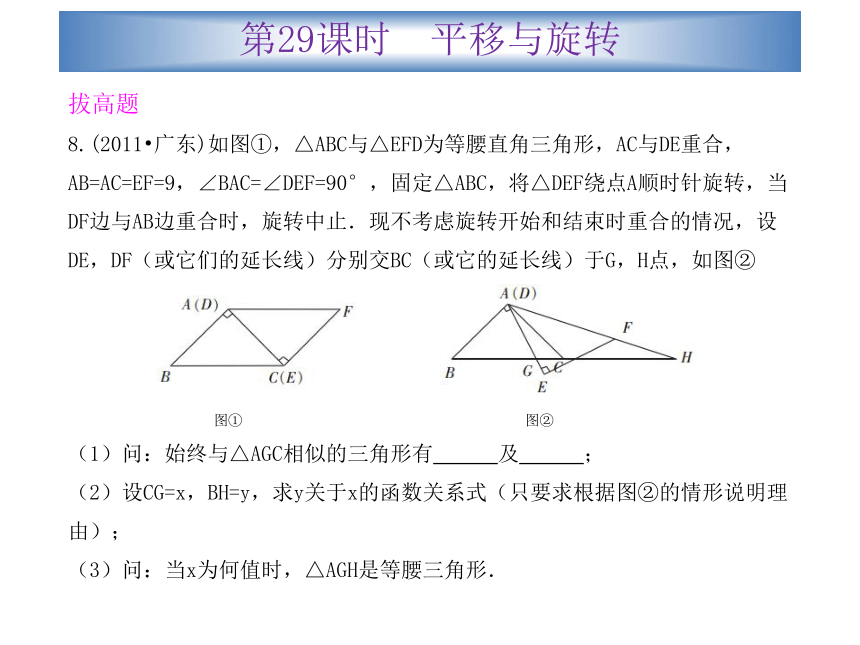
8.(2011?广东)如图①,△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线)于G,H点,如图②
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图②的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形.图①图②第29课时 平移与旋转(1)∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∴始终与△AGC相似的三角形有△HAB和△HGA;
故答案为:△HAB和△HGA.
(2)∵△AGC∽△HAB,∴ ,即 ,
∴?? .
答:y关于x的函数关系式为?? .
(3)∵∠GAH=45°,分两种情况讨论:
①当∠GAH=45°是等腰三角形的底角时,如图①:可知 ?????
②当∠GAH=45°是等腰三角形顶角时,如图②:由△HGA∽△HAB,??
知:HB=AB=9,也可知BG=HC,可得:???????.
答:当x为 和?? 时,△AGH是等腰三角形.图①图②第29课时 平移与旋转课时作业一、选择题
1.平面直角坐标中,坐标原点沿 轴向左平移3个单位后的对应点坐标为( )
A. (0,3) B. (0,-3) C. (3,0) D. (-3,0)
2.平面直角坐标中,点(3,0)绕原点逆时针旋转90°后,对应点的坐标为( )
A. (-3,0) B. (0,-3) C. (0,3) D. (3,-3)
3.在6×6的方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格DCD第29课时 平移与旋转课时作业4.由图中左侧三角形仅经过一次平移、旋转或轴对称变换,不能得到的图形是( )
5.如图,如果将△ABC的顶点A向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )
A.垂直 B.相等 C.平分 D.平分且垂直 DB第29课时 平移与旋转课时作业二、填空题
6.一个正方形要绕它的中心至少旋转_________度,才能和原来的图形重合.
7.点(3,-2)先向上平移2个单位长度,再向右平移3个单位长度后,对应点的坐标为 .8.如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=15°,∠C=10°,E,B,C在同一直线上,∠ABC=____________度,旋转角度是_____________度.9.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的有 个.10.如图,△ABC与△BDE都是等边三角形,AB<BD.如△ABC不动,将△BDE绕点B旋转,则在旋转过程中,你认为AE与CD的大小关系会怎样:________________.不变25(5,1)903155第29课时 平移与旋转课时作业三、解答题
11.如图,在方格纸中,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:先将格点△ABC向右平移4个单位得到△A1B1C1,再将△A1B1C1绕点C1点旋转180°得到△A2B2C2.
解:如图所示。
第29课时 平移与旋转课时作业12.如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角,∠AOA′=45°. 回答下列问题:
(1) 点B的对应点是点__________;
(2) 线段OB的对应线段是线段_________;
线段AB的对应线段是线段_________;
(3) ∠A的对应角是_______;∠B的对应角是_______;
(4) 旋转中心是点________;旋转的角度是______.
解:(1) 点B的对应点是点B′;
(2) 线段OB的对应线段是线段OB′;线段AB的对应线段是线段A′B′;
(3) ∠A的对应角是∠A′;∠B的对应角是∠B′;
(4) 旋转中心是点O;旋转的角度是45°.第29课时 平移与旋转课时作业13.如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,求∠BCA′的度数.
解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°﹣110°﹣40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°.第29课时 平移与旋转课时作业14.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.(1)解:FG⊥ED. 理由如下:
由旋转的性质,可得∠DEB=∠ACB,
由平移的性质,可得∠GFE=∠A,
∵∠ABC=90°, ∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°, ∴∠FHE=90°, ∴FG⊥ED;
(2)证:由旋转和平移的性质,
得∠GEF=∠CBE=∠ABC=90°,CG∥EB,CB=BE,
∴∠BCG+∠CBE=90°, ∴∠BCG=90°,
∴四边形BCGE是矩形,
又CB=BE, ∴四边形BCGE是正方形.结束谢谢!
考点分类一 图形的平移
【知识考点】
平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,图形的这种变换,叫做平移变换,简称平移,平移前后互相重合的点叫做对应点.
平移的性质:(1)对应线段平行(或共线) 相等,对应点所连的线段平行(或共线)且相等,图形上的点都沿同一方向移动了相同的距离;
(2)对应角相等;(3)平移前后的两个图形是全等图形.
【对应精练】1.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF ,则四边形ABFD的周长为( )
A.6 B.8 C.10 D.12C152.如图,将面积为5的△ABC沿BC方向平移至△DEF的位置,平移的距离是边BC长的两倍,那么图中的四边形ACED的面积为 .第29课时 平移与旋转考点分类二 图形的旋转
【知识考点】
旋转的概念:在平面内,把一个图形绕着一个定点着某个方向旋转一定的角度,图形的这种变换,叫做旋转变换,其中这个定点叫做旋转中心,这个角度叫做旋转角,旋转前后的点叫做对应点.
旋转的性质:
(1)图形上的每一点都绕着旋转中心,沿着相同的方向旋转同样的大小的角度;
(2)旋转后的图形与原来的图形的形状和大小都没有发生变化,即它们是全等的;
(3)旋转前后两个图形的对应点到旋转中心的距离相等;
(4)对应点到旋转中心的连线所成的角相等,并且等于旋转角.第29课时 平移与旋转【对应精练】
1.如图,在△ABC中,∠C=30°,将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于点F,则∠AFB= .2.如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D= .90°考点分类三 利用平移或旋转作图
【对应精练】
1.如图,边长为1的小正方形组成的方格纸上,将△ABC绕着点A顺时针旋转 .
(1)画出旋转后的△AB′C′;
(2)求线段AC在旋转过程中所扫过的扇形的面积.解:(1)如图所示:
(2)线段AC在旋转过程中所扫过的扇形的面积为? ?第29课时 平移与旋转真题演练?层层推进
基础题
1.(2012广东肇庆)点M(2,-1) 向上平移2个单位长度得到的点的坐标是( )
A. (2,0) B. (2,1) C. (2,2) D. (2,-3)
2.(2014佛山)若一个60°的角绕顶点旋转15°,则重叠部分的角的大小是( )
A.15° B.30° C.45° D.75°3.(2014梅州)如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D.若∠A′DC=90°,则∠A= .4.(2012广州)如图4,在等边△ABC中,AB=6,D是BC上一点,且BC=3BD,△ABD绕点A旋转后得到△ACE,则CE的长度为 。5.(2013广州)如图6,Rt△ABC的斜边AB=16, Rt△ABC绕点O顺时针旋转后得到Rt△A′B′C′,则Rt△A′B′C′的斜边A′B′上的中线长度为_____.图4图6BC2845°第29课时 平移与旋转提高题
6. (2014广东)如图,△ABC绕点A顺时针旋转45°得到△AB′C′,若BAC=90°,AB=AC= ,则图中阴影部分的面积等于 .7.(2011广东珠海)如图,将一个钝角△ABC(其中∠ABC=120°)绕点B顺时针旋转得△A1BC1,使得C点落在AB的延长线上的点C1处,连结AA1.
(1)写出旋转角的度数;(2)求证:∠A1AC=∠C1.(1)解:旋转角的度数为60°.
(2)证明:由题意可知:△ABC≌△A1BC1,∴A1B=AB,∠C=∠C1,
由(1)知:∠ABA1=60°,∴△A1BA为等边三角形.∴∠BAA1=60°.
而∠CBC1=60°,∴∠BAA1=∠CBC1,∴AA1∥BC. ∴∠A1AC=∠C.
又∵∠C=∠C1,∴∠A1AC=∠C1.第29课时 平移与旋转拔高题
8.(2011?广东)如图①,△ABC与△EFD为等腰直角三角形,AC与DE重合,AB=AC=EF=9,∠BAC=∠DEF=90°,固定△ABC,将△DEF绕点A顺时针旋转,当DF边与AB边重合时,旋转中止.现不考虑旋转开始和结束时重合的情况,设DE,DF(或它们的延长线)分别交BC(或它的延长线)于G,H点,如图②
(1)问:始终与△AGC相似的三角形有 及 ;
(2)设CG=x,BH=y,求y关于x的函数关系式(只要求根据图②的情形说明理由);
(3)问:当x为何值时,△AGH是等腰三角形.图①图②第29课时 平移与旋转(1)∵△ABC与△EFD为等腰直角三角形,AC与DE重合,
∴始终与△AGC相似的三角形有△HAB和△HGA;
故答案为:△HAB和△HGA.
(2)∵△AGC∽△HAB,∴ ,即 ,
∴?? .
答:y关于x的函数关系式为?? .
(3)∵∠GAH=45°,分两种情况讨论:
①当∠GAH=45°是等腰三角形的底角时,如图①:可知 ?????
②当∠GAH=45°是等腰三角形顶角时,如图②:由△HGA∽△HAB,??
知:HB=AB=9,也可知BG=HC,可得:???????.
答:当x为 和?? 时,△AGH是等腰三角形.图①图②第29课时 平移与旋转课时作业一、选择题
1.平面直角坐标中,坐标原点沿 轴向左平移3个单位后的对应点坐标为( )
A. (0,3) B. (0,-3) C. (3,0) D. (-3,0)
2.平面直角坐标中,点(3,0)绕原点逆时针旋转90°后,对应点的坐标为( )
A. (-3,0) B. (0,-3) C. (0,3) D. (3,-3)
3.在6×6的方格中,将图①中的图形N平移后位置如图②所示,则图形N的平移方法中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格DCD第29课时 平移与旋转课时作业4.由图中左侧三角形仅经过一次平移、旋转或轴对称变换,不能得到的图形是( )
5.如图,如果将△ABC的顶点A向下平移3格,再向左平移1格到达A′点,连接A′B,则线段A′B与线段AC的关系是( )
A.垂直 B.相等 C.平分 D.平分且垂直 DB第29课时 平移与旋转课时作业二、填空题
6.一个正方形要绕它的中心至少旋转_________度,才能和原来的图形重合.
7.点(3,-2)先向上平移2个单位长度,再向右平移3个单位长度后,对应点的坐标为 .8.如图,△ABC绕点B逆时针方向旋转到△EBD的位置,若∠A=15°,∠C=10°,E,B,C在同一直线上,∠ABC=____________度,旋转角度是_____________度.9.如图,将等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的有 个.10.如图,△ABC与△BDE都是等边三角形,AB<BD.如△ABC不动,将△BDE绕点B旋转,则在旋转过程中,你认为AE与CD的大小关系会怎样:________________.不变25(5,1)903155第29课时 平移与旋转课时作业三、解答题
11.如图,在方格纸中,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:先将格点△ABC向右平移4个单位得到△A1B1C1,再将△A1B1C1绕点C1点旋转180°得到△A2B2C2.
解:如图所示。
第29课时 平移与旋转课时作业12.如图,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段与角,∠AOA′=45°. 回答下列问题:
(1) 点B的对应点是点__________;
(2) 线段OB的对应线段是线段_________;
线段AB的对应线段是线段_________;
(3) ∠A的对应角是_______;∠B的对应角是_______;
(4) 旋转中心是点________;旋转的角度是______.
解:(1) 点B的对应点是点B′;
(2) 线段OB的对应线段是线段OB′;线段AB的对应线段是线段A′B′;
(3) ∠A的对应角是∠A′;∠B的对应角是∠B′;
(4) 旋转中心是点O;旋转的角度是45°.第29课时 平移与旋转课时作业13.如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°.∠B′=110°,求∠BCA′的度数.
解:根据旋转的性质可得:∠A′=∠A,∠A′CB′=∠ACB,
∵∠A=40°,
∴∠A′=40°,
∵∠B′=110°,
∴∠A′CB′=180°﹣110°﹣40°=30°,
∴∠ACB=30°,
∵将△ABC绕着点C顺时针旋转50°后得到△A′B′C′,
∴∠ACA′=50°,
∴∠BCA′=30°+50°=80°.第29课时 平移与旋转课时作业14.如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DF、FG相交于点H.
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.(1)解:FG⊥ED. 理由如下:
由旋转的性质,可得∠DEB=∠ACB,
由平移的性质,可得∠GFE=∠A,
∵∠ABC=90°, ∴∠A+∠ACB=90°,
∴∠DEB+∠GFE=90°, ∴∠FHE=90°, ∴FG⊥ED;
(2)证:由旋转和平移的性质,
得∠GEF=∠CBE=∠ABC=90°,CG∥EB,CB=BE,
∴∠BCG+∠CBE=90°, ∴∠BCG=90°,
∴四边形BCGE是矩形,
又CB=BE, ∴四边形BCGE是正方形.结束谢谢!
同课章节目录
