广东省2015中考数学冲刺复习课件:第28课时 弧长与扇形面积的计算(共19张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第28课时 弧长与扇形面积的计算(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 819.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:08:36 | ||
图片预览






文档简介
课件19张PPT。数学
第28课时 弧长与扇形面积的计算第28课时 弧长与扇形面积的计算知识考点?对应精练
考点分类一 扇形的面积、弧长
【知识考点】
1.如果弧长为l,圆心角为n°,圆的半径为r,那么弧长的计算公式为:
.
【对应精练】
1. 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,
则劣弧 BC的长是 .第28课时 弧长与扇形面积的计算【知识考点】
2.由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形.
若扇形的圆心角为n°,所在圆半径为r,弧长为l,面积为S,
则S= ,或S= lr.
【对应精练】
2. 已知扇形的圆心角为30°,面积为3π㎝2,则扇形的弧长是 ㎝。π第28课时 弧长与扇形面积的计算考点分类二 求阴影部分的面积
【知识考点】
1. 规则图形:按规则图形的面积公式求.
【对应精练】1. 如图,⊙A、⊙B、⊙C两两外切,它们的半径都是a,顺次连接三个圆心,则图中阴影部分的面积是 .提示:⊙A、⊙B、⊙C两两外切,它们的半径都是a,且三角形内角和定理为180°,
∴阴影部分的面积是半圆的面积,即为 。第28课时 弧长与扇形面积的计算【知识考点】
2.不规则图形:采用“转化”的数学思想方法,把不规则图形的面积采用“割补法”、“等积变形法”、“平移法”、“旋转法”等转化为规则图形的面积.
【对应精练】2.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为 .提示:连接OE、DO、AE,
∵AB是直径,∴∠AEB=90°,
又∵∠BED=120°,∴∠AED=30°,∴∠AOD=2∠AED=60°.
∵OA=OD ∴△AOD是等边三角形,∴∠A=60°,
∵点E为BC的中点,∠AED=90°,∴AB=AC,
∴△ABC是等边三角形.△EDC是等边三角形,边长是4.
∴∠BOE=∠EOD=60°,
∴ 和弦BE围成的部分的面积= 和弦DE围成的部分的面积.
∴阴影部分的面积=S△EDC= ×22= .第28课时 弧长与扇形面积的计算考点分类三 正多边形与圆
【知识考点】
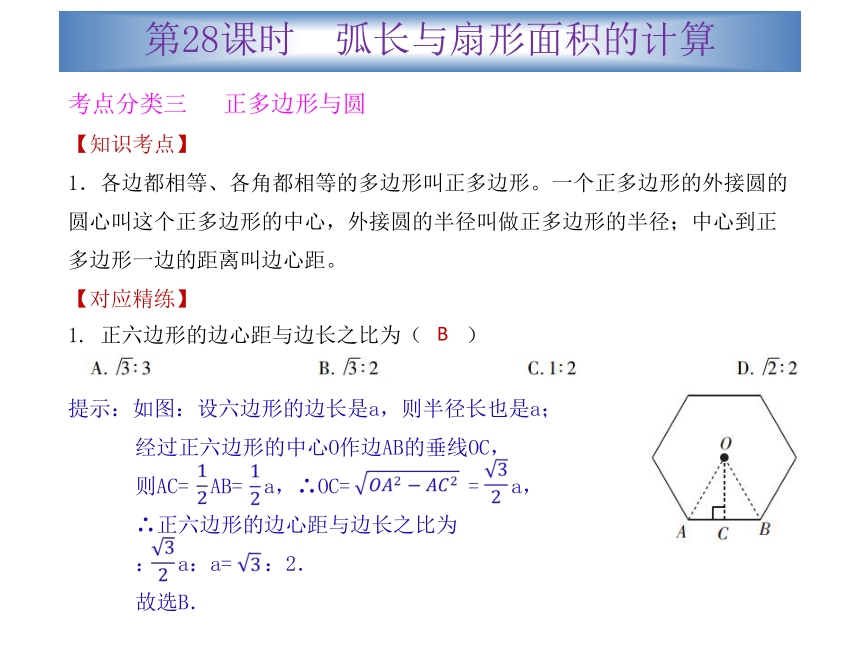
1.各边都相等、各角都相等的多边形叫正多边形。一个正多边形的外接圆的圆心叫这个正多边形的中心,外接圆的半径叫做正多边形的半径;中心到正多边形一边的距离叫边心距。
【对应精练】1. 正六边形的边心距与边长之比为( )
提示:如图:设六边形的边长是a,则半径长也是a;
经过正六边形的中心O作边AB的垂线OC,
则AC= AB= a,∴OC= = a,
∴正六边形的边心距与边长之比为
: a:a= :2.
故选B.B第27课时 直线与圆的位置关系真题演练?层层推进
基础题
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π提示:根据弧长公式 , =3π.2.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则 的长为( )
A.π B. C.7π D.6π3. (广东珠海?2014年)已知圆柱体的底面半径为3cm,髙为4cm,则圆柱体的侧面积为( )
A、24πcm2 B、36πcm2 C、12cm2 D、24cm2CA提示:根据弧长公式代入即可.提示:圆柱的侧面积=2π×3×4=24π.故选A.A第28课时 弧长与扇形面积的计算4.(广东?2013年)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是__________(结果保留π).提示:将左下阴影部分对称移到右上角,则阴影部分面积的和为:
S=5.半径为4cm,圆心角为60°的扇形的面积为 cm2.提高题
6、(佛山?2013年)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.提示:半径为4cm,圆心角为60°的扇形的面积为: (cm2).解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,∴l=2r,
∴母线与高的夹角的正弦值= = ,∴母线AB与高AO的夹角30°.第28课时 弧长与扇形面积的计算7.(广东梅州?2013年)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.解:(1)∵在矩形ABCD中,AB=2DA,
∴AE=2AD,且∠ADE=90°.
又∵DA=2,∴AE=AB=4,
∴DE= ,
∴EC=DC-DE=4- .
(2)S阴影=S扇形AEF -S△ADE= .第28课时 弧长与扇形面积的计算拔高题
8. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.求图中阴影部分的面积.解:连接OC,OC交BD于E,
∵∠CDB=30°,∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,∴CD∥AB,
又∵AC∥BD,∴四边形ABDC为平行四边形,∴∠A=∠D=30°,
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC
∵AC∥BD, ∴OC⊥BD,∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=6,
∴BE=OBcos30°=3 ,∴BD=2BE=6 ;易证△OEB≌△CED,
∴S阴影=S扇形BOC∴S阴影= =6π.
答:阴影部分的面积是6π.第28课时 弧长与扇形面积的计算课时作业一、选择题
1. 一个正多边形的每个外角都等于36°,那么它是( )
A、正六边形 B、正八边形 C、正十边形 D、 正十二边形提示:360÷36=10.2.如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )
A. B. C. D. 提示: ∵AB是⊙O的切线,切点为A,∴OA⊥AB,即∠OAB=90°。
∵在Rt△AOB中,OA=1,∠AOB=600,∴AB= OAtan∠AOB= 。
∴S阴影部分=S△AOB–S扇形OAC= 。
故选C。CC第28课时 弧长与扇形面积的计算课时作业3. 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为: ( )
A.10π B. C. D.π提示:△ABC绕点C顺时针旋转60°,顶点A经过的路径是以C为圆心AC为半径,圆心角为60°的弧,根据弧长公式 ,可求路径长为 .4.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( ).
A. B. C. D.提示:图中阴影部分的面积等于:三角形AOB面积-扇形AOB面积,不难知道,?AOB为等边三角形,可求出?AOB边AB上的高是 ,扇形AOB圆心角∠O=60°,半径OA= ,
从而阴影部分的面积是 ,故选A.CA第28课时 弧长与扇形面积的计算课时作业5.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A、6, B、 ,3 C、6,3 D、 , 提示:∵正方形的边长为6,∴AB=3,
又∵∠AOB=45°,∴OB=3 ∴AO=二、填空题
6.在半径为6cm的圆中,60o圆心角所对的弧长为 cm.(结果保留π)提示:根据弧长公式 .B2π7. (2013重庆)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为___________(结果保留π)3π8. (2013广东肇庆)扇形的半径是9 cm ,弧长是3πcm,则此扇形的圆心角为 度.60提示:由弧长公式 ,可求得n=60.第28课时 弧长与扇形面积的计算课时作业9.在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .提示:将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过部分的形状为半径为2,圆心角度数为30°的两个扇形,其面积为 .10.如图,已知扇形的圆心角为60°,半径为 ,则图中弓形的面积为 。提示:过A作AD⊥CB,
∵∠CAB=60°,AC=AB,∴△ABC是等边三角形,
∵AC= ,∴AD=AC?sin60°= ,
∴△ABC面积: ,
∵扇形面积: ,
∴弓形的面积为: .第28课时 弧长与扇形面积的计算课时作业三、解答题
11.如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.解:(1)∵∠ABC与∠D都是弧AC所对的圆周角 ∴∠ABC=∠D =60°
(2)∵AB是⊙O的直径 ∴∠ACB=90° ∴∠BAC=30°
∴∠BAE =∠BAC+∠EAC=30°+60°=90°
即BA⊥AE ∴AE是⊙O的切线
(3)如图,连结OC
∵OB=OC,∠ABC=60°∴△OBC是等边三角形
∴OB=BC=4 , ∠BOC=60° ∴∠AOC=120°
∴劣弧AC的长为 第28课时 弧长与扇形面积的计算课时作业12. 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)解:连接OC,
∵AB与圆O相切,∴OC⊥AB,
∵OA=OB,∴∠AOC=∠BOC,∠A=∠B=30°,
在Rt△AOC中,∠A=30°,OA=4,∴OC= OA=2,∠AOC=60°,
∴∠AOB=120°,AC= =2 ,即AB=2AC=4 ,
则S阴影=S△AOB﹣S扇形= .第28课时 弧长与扇形面积的计算课时作业13.如图,有一直径是 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.解:(1)∵∠BAC=90°,∴BC为⊙O的直径,即BC= ,
∴AB= BC=1;
(2)设所得圆锥的底面圆的半径为r,
根据题意得2πr= ,解得r= .第28课时 弧长与扇形面积的计算课时作业14. 分别作出已知三角形的内切圆、外接圆。解:如图:结束谢谢!
考点分类一 扇形的面积、弧长
【知识考点】
1.如果弧长为l,圆心角为n°,圆的半径为r,那么弧长的计算公式为:
.
【对应精练】
1. 如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,
则劣弧 BC的长是 .第28课时 弧长与扇形面积的计算【知识考点】
2.由组成圆心角的两条半径和圆心角所对弧围成的图形叫做扇形.
若扇形的圆心角为n°,所在圆半径为r,弧长为l,面积为S,
则S= ,或S= lr.
【对应精练】
2. 已知扇形的圆心角为30°,面积为3π㎝2,则扇形的弧长是 ㎝。π第28课时 弧长与扇形面积的计算考点分类二 求阴影部分的面积
【知识考点】
1. 规则图形:按规则图形的面积公式求.
【对应精练】1. 如图,⊙A、⊙B、⊙C两两外切,它们的半径都是a,顺次连接三个圆心,则图中阴影部分的面积是 .提示:⊙A、⊙B、⊙C两两外切,它们的半径都是a,且三角形内角和定理为180°,
∴阴影部分的面积是半圆的面积,即为 。第28课时 弧长与扇形面积的计算【知识考点】
2.不规则图形:采用“转化”的数学思想方法,把不规则图形的面积采用“割补法”、“等积变形法”、“平移法”、“旋转法”等转化为规则图形的面积.
【对应精练】2.如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为 .提示:连接OE、DO、AE,
∵AB是直径,∴∠AEB=90°,
又∵∠BED=120°,∴∠AED=30°,∴∠AOD=2∠AED=60°.
∵OA=OD ∴△AOD是等边三角形,∴∠A=60°,
∵点E为BC的中点,∠AED=90°,∴AB=AC,
∴△ABC是等边三角形.△EDC是等边三角形,边长是4.
∴∠BOE=∠EOD=60°,
∴ 和弦BE围成的部分的面积= 和弦DE围成的部分的面积.
∴阴影部分的面积=S△EDC= ×22= .第28课时 弧长与扇形面积的计算考点分类三 正多边形与圆
【知识考点】
1.各边都相等、各角都相等的多边形叫正多边形。一个正多边形的外接圆的圆心叫这个正多边形的中心,外接圆的半径叫做正多边形的半径;中心到正多边形一边的距离叫边心距。
【对应精练】1. 正六边形的边心距与边长之比为( )
提示:如图:设六边形的边长是a,则半径长也是a;
经过正六边形的中心O作边AB的垂线OC,
则AC= AB= a,∴OC= = a,
∴正六边形的边心距与边长之比为
: a:a= :2.
故选B.B第27课时 直线与圆的位置关系真题演练?层层推进
基础题
1.已知扇形的圆心角为45°,半径长为12,则该扇形的弧长为( )
A. B.2π C.3π D.12π提示:根据弧长公式 , =3π.2.如图,在4×4的正方形网格中,若将△ABC绕着点A逆时针旋转得到△AB′C′,则 的长为( )
A.π B. C.7π D.6π3. (广东珠海?2014年)已知圆柱体的底面半径为3cm,髙为4cm,则圆柱体的侧面积为( )
A、24πcm2 B、36πcm2 C、12cm2 D、24cm2CA提示:根据弧长公式代入即可.提示:圆柱的侧面积=2π×3×4=24π.故选A.A第28课时 弧长与扇形面积的计算4.(广东?2013年)如图,三个小正方形的边长都为1,则图中阴影部分面积的和是__________(结果保留π).提示:将左下阴影部分对称移到右上角,则阴影部分面积的和为:
S=5.半径为4cm,圆心角为60°的扇形的面积为 cm2.提高题
6、(佛山?2013年)如图,圆锥的侧面展开图是一个半圆,求母线AB与高AO的夹角.参考公式:圆锥的侧面积S=πrl,其中r为底面半径,l为母线长.提示:半径为4cm,圆心角为60°的扇形的面积为: (cm2).解:设圆锥的母线长为l,底面半径为r,
则:πl=2πr,∴l=2r,
∴母线与高的夹角的正弦值= = ,∴母线AB与高AO的夹角30°.第28课时 弧长与扇形面积的计算7.(广东梅州?2013年)如图,在矩形ABCD中,AB=2DA,以点A为圆心,AB为半径的圆弧交DC于点E,交AD的延长线于点F,设DA=2.
(1)求线段EC的长;
(2)求图中阴影部分的面积.解:(1)∵在矩形ABCD中,AB=2DA,
∴AE=2AD,且∠ADE=90°.
又∵DA=2,∴AE=AB=4,
∴DE= ,
∴EC=DC-DE=4- .
(2)S阴影=S扇形AEF -S△ADE= .第28课时 弧长与扇形面积的计算拔高题
8. 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.求图中阴影部分的面积.解:连接OC,OC交BD于E,
∵∠CDB=30°,∴∠COB=2∠CDB=60°,
∵∠CDB=∠OBD,∴CD∥AB,
又∵AC∥BD,∴四边形ABDC为平行四边形,∴∠A=∠D=30°,
∴∠OCA=180°﹣∠A﹣∠COB=90°,即OC⊥AC
∵AC∥BD, ∴OC⊥BD,∴BE=DE,
∵在直角△BEO中,∠OBD=30°,OB=6,
∴BE=OBcos30°=3 ,∴BD=2BE=6 ;易证△OEB≌△CED,
∴S阴影=S扇形BOC∴S阴影= =6π.
答:阴影部分的面积是6π.第28课时 弧长与扇形面积的计算课时作业一、选择题
1. 一个正多边形的每个外角都等于36°,那么它是( )
A、正六边形 B、正八边形 C、正十边形 D、 正十二边形提示:360÷36=10.2.如图,AB是⊙O的切线,切点为A,OA=1,∠AOB=60°,则图中阴影部分的面积是( )
A. B. C. D. 提示: ∵AB是⊙O的切线,切点为A,∴OA⊥AB,即∠OAB=90°。
∵在Rt△AOB中,OA=1,∠AOB=600,∴AB= OAtan∠AOB= 。
∴S阴影部分=S△AOB–S扇形OAC= 。
故选C。CC第28课时 弧长与扇形面积的计算课时作业3. 如图,在边长为1的正方形组成的网格中,△ABC的顶点都在格点上,将△ABC绕点C顺时针旋转60°,则顶点A所经过的路径长为: ( )
A.10π B. C. D.π提示:△ABC绕点C顺时针旋转60°,顶点A经过的路径是以C为圆心AC为半径,圆心角为60°的弧,根据弧长公式 ,可求路径长为 .4.如图,⊙O的外切正六边形ABCDEF的边长为2,则图中阴影部分的面积为( ).
A. B. C. D.提示:图中阴影部分的面积等于:三角形AOB面积-扇形AOB面积,不难知道,?AOB为等边三角形,可求出?AOB边AB上的高是 ,扇形AOB圆心角∠O=60°,半径OA= ,
从而阴影部分的面积是 ,故选A.CA第28课时 弧长与扇形面积的计算课时作业5.若正方形的边长为6,则其外接圆半径与内切圆半径的大小分别为( )
A、6, B、 ,3 C、6,3 D、 , 提示:∵正方形的边长为6,∴AB=3,
又∵∠AOB=45°,∴OB=3 ∴AO=二、填空题
6.在半径为6cm的圆中,60o圆心角所对的弧长为 cm.(结果保留π)提示:根据弧长公式 .B2π7. (2013重庆)一个扇形的圆心角为120°,半径为3,则这个扇形的面积为___________(结果保留π)3π8. (2013广东肇庆)扇形的半径是9 cm ,弧长是3πcm,则此扇形的圆心角为 度.60提示:由弧长公式 ,可求得n=60.第28课时 弧长与扇形面积的计算课时作业9.在平面内,将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过的面积为 .提示:将长度为4的线段AB绕它的中点M,按逆时针方向旋转30°,则线段AB扫过部分的形状为半径为2,圆心角度数为30°的两个扇形,其面积为 .10.如图,已知扇形的圆心角为60°,半径为 ,则图中弓形的面积为 。提示:过A作AD⊥CB,
∵∠CAB=60°,AC=AB,∴△ABC是等边三角形,
∵AC= ,∴AD=AC?sin60°= ,
∴△ABC面积: ,
∵扇形面积: ,
∴弓形的面积为: .第28课时 弧长与扇形面积的计算课时作业三、解答题
11.如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.解:(1)∵∠ABC与∠D都是弧AC所对的圆周角 ∴∠ABC=∠D =60°
(2)∵AB是⊙O的直径 ∴∠ACB=90° ∴∠BAC=30°
∴∠BAE =∠BAC+∠EAC=30°+60°=90°
即BA⊥AE ∴AE是⊙O的切线
(3)如图,连结OC
∵OB=OC,∠ABC=60°∴△OBC是等边三角形
∴OB=BC=4 , ∠BOC=60° ∴∠AOC=120°
∴劣弧AC的长为 第28课时 弧长与扇形面积的计算课时作业12. 如图,△OAB中,OA=OB=4,∠A=30°,AB与⊙O相切于点C,求图中阴影部分的面积.(结果保留π)解:连接OC,
∵AB与圆O相切,∴OC⊥AB,
∵OA=OB,∴∠AOC=∠BOC,∠A=∠B=30°,
在Rt△AOC中,∠A=30°,OA=4,∴OC= OA=2,∠AOC=60°,
∴∠AOB=120°,AC= =2 ,即AB=2AC=4 ,
则S阴影=S△AOB﹣S扇形= .第28课时 弧长与扇形面积的计算课时作业13.如图,有一直径是 米的圆形铁皮,现从中剪出一个圆周角是90°的最大扇形ABC,则:
(1)求AB的长;
(2)用该扇形铁皮围成一个圆锥,求所得圆锥的底面圆的半径.解:(1)∵∠BAC=90°,∴BC为⊙O的直径,即BC= ,
∴AB= BC=1;
(2)设所得圆锥的底面圆的半径为r,
根据题意得2πr= ,解得r= .第28课时 弧长与扇形面积的计算课时作业14. 分别作出已知三角形的内切圆、外接圆。解:如图:结束谢谢!
同课章节目录
