广东省2015中考数学冲刺复习课件:第26课时 圆的基本性质(共14张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第26课时 圆的基本性质(共14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 710.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:09:55 | ||
图片预览





文档简介
课件14张PPT。数学
第26课时 圆的基本性质第26课时 圆的基本性质知识考点?对应精练
考点分类一 圆的基本性质圆的对称性
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
(2)圆是以圆心为对称中心的中心对称图形.
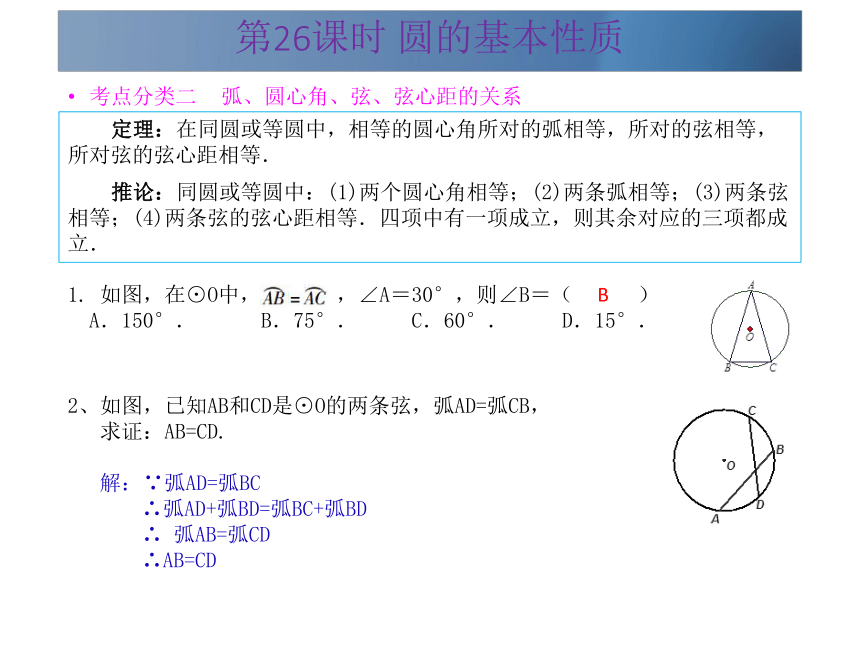
(3)圆是旋转对称图形.圆绕圆心旋转任意角度,都能和原来的图形重合,这就是圆的旋转不变性.1. (广东省?2013年) 下列图形中,不是轴对称图形的是( ) C解析:圆和正方形都既是轴对称图形又是中心对称图形,等边三角形是轴对称图形,平行四边形是中心对称图形,故选C。第26课时 圆的基本性质考点分类二 弧、圆心角、弦、弦心距的关系 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
推论:同圆或等圆中:(1)两个圆心角相等;(2)两条弧相等;(3)两条弦相等;(4)两条弦的弦心距相等.四项中有一项成立,则其余对应的三项都成立.1. 如图,在⊙O中, ,∠A=30°,则∠B=( )
A.150°. B.75°. C.60°. D.15°.解:∵弧AD=弧BC
∴弧AD+弧BD=弧BC+弧BD
∴ 弧AB=弧CD
∴AB=CD2、如图,已知AB和CD是⊙O的两条弦,弧AD=弧CB,
求证:AB=CD.B第26课时 圆的基本性质考点分类三 垂径定理 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;弦的垂直平分线经过圆心,并且平分弦所对的两条弧;平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧.1. 如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为( )
(A)6 (B)8 (C)10 (D)122.如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB 的长是( )
A.2cm B.3cm C.4cm D. cmA?C第26课时 圆的基本性质考点分类四 圆周角性质(1)圆心角的度数等于它所对弧的度数;
(2)一条弧所对的圆周角的度数等于它所对圆心角的度数的一半;
(3)同弧或等弧所对的圆周角相等,同圆或等圆中相等的圆周角所对的弧也相等;
(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆内接四边形对角互补;每一个内角,等于它的外对角。1.如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
(A)40° (B)50° (C)80° (D)100°2.一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=50°,则这个人工湖的直径AD为( )
A. B.
C. D. DB提示:连接BD.????第26课时 圆的基本性质真题演练?层层推进
基础题1. 佛山?2013年)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )
A. 3 B. 4 C. D. ??如图所示:过点O作OD⊥AB于点D,∵OB=3,AB=3,OD⊥AB,
∴ ,
在Rt△BOD中, .故选C.??C2. (湛江?2013年)如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
A.25° B.35° C.55° D.70°3. (珠海?2013年) 如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接BE,则∠AEB的度数为( )
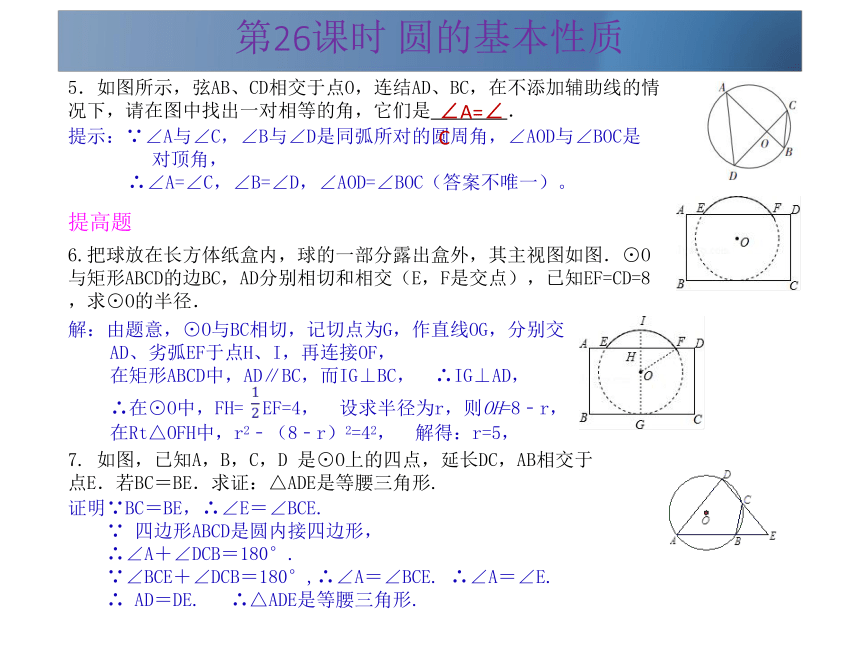
A.36° B.46° C.27° D.63°4、(珠海?2014)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于 .∵线段AB是⊙O的直径,弦CD丄AB,∴ ,∵∠CAB=20°,∴∠BOD=40°,∴∠AOD=140°.BA140°第26课时 圆的基本性质 5.如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是 .提示:∵∠A与∠C,∠B与∠D是同弧所对的圆周角,∠AOD与∠BOC是对顶角,
∴∠A=∠C,∠B=∠D,∠AOD=∠BOC(答案不唯一)。6.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,求⊙O的半径.解:由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧EF于点H、I,再连接OF,
在矩形ABCD中,AD∥BC,而IG⊥BC, ∴IG⊥AD,
∴在⊙O中,FH= EF=4, 设求半径为r,则OH=8﹣r,
在Rt△OFH中,r2﹣(8﹣r)2=42, 解得:r=5,∠A=∠C提高题?7. 如图,已知A,B,C,D 是⊙O上的四点,延长DC,AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.证明∵BC=BE,∴∠E=∠BCE.
∵ 四边形ABCD是圆内接四边形,
∴∠A+∠DCB=180°.
∵∠BCE+∠DCB=180°,∴∠A=∠BCE. ∴∠A=∠E.
∴ AD=DE. ∴△ADE是等腰三角形. 第26课时 圆的基本性质拔高题8. 如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出弧AB所在圆O的半径。解:∵弓形的跨度AB=3m,EF为弓形的高,
∴OE⊥AB,
∴AF= AB= m,
∵ 所在圆O的半径为r,弓形的高EF=1m,
∴AO=r,OF=r-1,
在Rt△AOF中,AO2=AF2+OF2,
即 ,
解得r= (m).
答: 所在圆O的半径为 m.?????第26课时 圆的基本性质课时作业一、选择题1. 已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.25° D.20°2. 如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位3. 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A.30° B.45° C.60° D.70°提示:∵∠ABC= ∠AOC, 而∠ABC+∠AOC=90°,
∴ ∠AOC+∠AOC=90°,
∴∠AOC=60°. 故选C.4.如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( )
A.50° B.80°或50° C.130° D.50°或130°ACBDD??5. 如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.弧CB=弧BD C.∠ACD=∠ADC D.OM=MD第26课时 圆的基本性质课时作业二、填空题6. (2014年广东卷).在⊙O中,已知半径为5,弦AB的长为8,那么圆心O 到AB的距离为 ;7. (佛山?2013年)图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD= .8. (2014?黄冈)如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD= .提示:连结OD,设⊙O的半径为R,
∵∠BAD=30°,
∴∠BOD=2∠BAD=60°,
∵CD⊥AB,∴DE=CE,
在Rt△ODE中,OE=OB﹣BE=R﹣2,OD=R,
∵cos∠EOD=cos60°= ,
∴ ,解得R=4,
∴OE=4﹣2=2, ∴DE= OE=2 , ∴CD=2DE=4 .3?60°?解:∵CA∥OB,∴∠CAO=∠AOB=30°,
∵OA=OC,∴∠C=∠OAC=30°,∴∠AOD=2∠C=60°,
∴∠BOD=60°﹣30°=30°.????第26课时 圆的基本性质课时作业 9.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50° ,则∠OCD的度数是 .10.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .提示:连接OB,由垂径定理得弧BC等于弧BD,再由“同圆中等弧所对的圆心角相等”得∠COD=∠A=50°,
最后∠OCD=90°-∠COD=90°-50°=40°.提示:本题给出直角三角形的两边长分别为16和12,并未给出具体是斜边和直角边还是两直角边,故需分类讨论:①当16和12是两直角边时,可得此直角三角形的斜边为20;②当16和12是斜边和直角边时,最后由直角三角形的外接圆半径即为直角三角形斜边的一半.故得答案10或8.40°10或811. (2013年广州市)如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为 ,求点P的坐标.?解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA, ∴OD= OA=3,
在Rt△OPD中, ∵OP= ,OD=3,
∴ ,
∴P(3,2).三、解答题???第26课时 圆的基本性质课时作业 12.如图, AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,求CD的长.解:∵OC⊥AP,OD⊥PB,
∴由垂径定理得:AC=PC,PD=BD,
∴CD是△APB的中位线,
∴CD= AB= ×8=4.13. (2013陕西)如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,求OP的长。解:连接OB,过O作OF⊥CD于点 ,作OE⊥AB于点E,
则:BE= AB= ×8=4,
在Rt△OEB中,由勾股定理可得:
,
∵AB=CD
∴OE=OF
∵∠OEP=∠FPE=∠PEO
∴四边形OEPF为正方形
∴OP= OE= . ???????第26课时 圆的基本性质课时作业 14.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.解:(1)∵AB是半圆O的直径,∴∠ACB=90°,
又∵OD∥BC,∴∠AEO=90°,
即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°.
∵OA=OD,∴∠DAO=∠ADO= =55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;(2)在直角△ABC中,BC= .
∵OE⊥AC,∴AE=EC,
又∵OA=OB,∴OE= BC= .
又∵OD= AB=2,∴DE=OD﹣OE=2﹣ .??????结束谢谢!
考点分类一 圆的基本性质圆的对称性
(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.
(2)圆是以圆心为对称中心的中心对称图形.
(3)圆是旋转对称图形.圆绕圆心旋转任意角度,都能和原来的图形重合,这就是圆的旋转不变性.1. (广东省?2013年) 下列图形中,不是轴对称图形的是( ) C解析:圆和正方形都既是轴对称图形又是中心对称图形,等边三角形是轴对称图形,平行四边形是中心对称图形,故选C。第26课时 圆的基本性质考点分类二 弧、圆心角、弦、弦心距的关系 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等.
推论:同圆或等圆中:(1)两个圆心角相等;(2)两条弧相等;(3)两条弦相等;(4)两条弦的弦心距相等.四项中有一项成立,则其余对应的三项都成立.1. 如图,在⊙O中, ,∠A=30°,则∠B=( )
A.150°. B.75°. C.60°. D.15°.解:∵弧AD=弧BC
∴弧AD+弧BD=弧BC+弧BD
∴ 弧AB=弧CD
∴AB=CD2、如图,已知AB和CD是⊙O的两条弦,弧AD=弧CB,
求证:AB=CD.B第26课时 圆的基本性质考点分类三 垂径定理 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.
推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;弦的垂直平分线经过圆心,并且平分弦所对的两条弧;平分弦所对的一条弧的直径垂直平分弦,并且平分弦所对的另一条弧.1. 如图,半径为10的⊙O中,弦AB的长为16,则这条弦的弦心距为( )
(A)6 (B)8 (C)10 (D)122.如图,⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,OM:OD=3:5,则AB 的长是( )
A.2cm B.3cm C.4cm D. cmA?C第26课时 圆的基本性质考点分类四 圆周角性质(1)圆心角的度数等于它所对弧的度数;
(2)一条弧所对的圆周角的度数等于它所对圆心角的度数的一半;
(3)同弧或等弧所对的圆周角相等,同圆或等圆中相等的圆周角所对的弧也相等;
(4)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.
圆内接四边形对角互补;每一个内角,等于它的外对角。1.如图,点A,B,C在⊙O上,∠A=50°,则∠BOC的度数为( )
(A)40° (B)50° (C)80° (D)100°2.一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=50°,则这个人工湖的直径AD为( )
A. B.
C. D. DB提示:连接BD.????第26课时 圆的基本性质真题演练?层层推进
基础题1. 佛山?2013年)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是( )
A. 3 B. 4 C. D. ??如图所示:过点O作OD⊥AB于点D,∵OB=3,AB=3,OD⊥AB,
∴ ,
在Rt△BOD中, .故选C.??C2. (湛江?2013年)如图,AB是⊙O的直径,∠AOC=110°,则∠D=( )
A.25° B.35° C.55° D.70°3. (珠海?2013年) 如图,□ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,∠ADC=54°,连接BE,则∠AEB的度数为( )
A.36° B.46° C.27° D.63°4、(珠海?2014)如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于 .∵线段AB是⊙O的直径,弦CD丄AB,∴ ,∵∠CAB=20°,∴∠BOD=40°,∴∠AOD=140°.BA140°第26课时 圆的基本性质 5.如图所示,弦AB、CD相交于点O,连结AD、BC,在不添加辅助线的情况下,请在图中找出一对相等的角,它们是 .提示:∵∠A与∠C,∠B与∠D是同弧所对的圆周角,∠AOD与∠BOC是对顶角,
∴∠A=∠C,∠B=∠D,∠AOD=∠BOC(答案不唯一)。6.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,求⊙O的半径.解:由题意,⊙O与BC相切,记切点为G,作直线OG,分别交AD、劣弧EF于点H、I,再连接OF,
在矩形ABCD中,AD∥BC,而IG⊥BC, ∴IG⊥AD,
∴在⊙O中,FH= EF=4, 设求半径为r,则OH=8﹣r,
在Rt△OFH中,r2﹣(8﹣r)2=42, 解得:r=5,∠A=∠C提高题?7. 如图,已知A,B,C,D 是⊙O上的四点,延长DC,AB相交于点E.若BC=BE.求证:△ADE是等腰三角形.证明∵BC=BE,∴∠E=∠BCE.
∵ 四边形ABCD是圆内接四边形,
∴∠A+∠DCB=180°.
∵∠BCE+∠DCB=180°,∴∠A=∠BCE. ∴∠A=∠E.
∴ AD=DE. ∴△ADE是等腰三角形. 第26课时 圆的基本性质拔高题8. 如图所示,某窗户由矩形和弓形组成,已知弓形的跨度AB=3m,弓形的高EF=1m,现计划安装玻璃,请帮工程师求出弧AB所在圆O的半径。解:∵弓形的跨度AB=3m,EF为弓形的高,
∴OE⊥AB,
∴AF= AB= m,
∵ 所在圆O的半径为r,弓形的高EF=1m,
∴AO=r,OF=r-1,
在Rt△AOF中,AO2=AF2+OF2,
即 ,
解得r= (m).
答: 所在圆O的半径为 m.?????第26课时 圆的基本性质课时作业一、选择题1. 已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
A.45° B.35° C.25° D.20°2. 如图,小华同学设计了一个圆直径的测量器,标有刻度的尺子OA、OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A. 12个单位 B. 10个单位 C.4个单位 D. 15个单位3. 如图,△ABC的顶点A、B、C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC的大小是( )
A.30° B.45° C.60° D.70°提示:∵∠ABC= ∠AOC, 而∠ABC+∠AOC=90°,
∴ ∠AOC+∠AOC=90°,
∴∠AOC=60°. 故选C.4.如图,∠AOB=100°,点C在⊙O上,且点C不与A、B重合,则∠ACB的度数为( )
A.50° B.80°或50° C.130° D.50°或130°ACBDD??5. 如图,AB是⊙的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B.弧CB=弧BD C.∠ACD=∠ADC D.OM=MD第26课时 圆的基本性质课时作业二、填空题6. (2014年广东卷).在⊙O中,已知半径为5,弦AB的长为8,那么圆心O 到AB的距离为 ;7. (佛山?2013年)图中圆心角∠AOB=30°,弦CA∥OB,延长CO与圆交于点D,则∠BOD= .8. (2014?黄冈)如图,在⊙O中,弦CD垂直于直径AB于点E,若∠BAD=30°,且BE=2,则CD= .提示:连结OD,设⊙O的半径为R,
∵∠BAD=30°,
∴∠BOD=2∠BAD=60°,
∵CD⊥AB,∴DE=CE,
在Rt△ODE中,OE=OB﹣BE=R﹣2,OD=R,
∵cos∠EOD=cos60°= ,
∴ ,解得R=4,
∴OE=4﹣2=2, ∴DE= OE=2 , ∴CD=2DE=4 .3?60°?解:∵CA∥OB,∴∠CAO=∠AOB=30°,
∵OA=OC,∴∠C=∠OAC=30°,∴∠AOD=2∠C=60°,
∴∠BOD=60°﹣30°=30°.????第26课时 圆的基本性质课时作业 9.如图,△ABC内接于⊙O,OD⊥BC于D,∠A=50° ,则∠OCD的度数是 .10.直角三角形的两边长分别为16和12,则此三角形的外接圆半径是 .提示:连接OB,由垂径定理得弧BC等于弧BD,再由“同圆中等弧所对的圆心角相等”得∠COD=∠A=50°,
最后∠OCD=90°-∠COD=90°-50°=40°.提示:本题给出直角三角形的两边长分别为16和12,并未给出具体是斜边和直角边还是两直角边,故需分类讨论:①当16和12是两直角边时,可得此直角三角形的斜边为20;②当16和12是斜边和直角边时,最后由直角三角形的外接圆半径即为直角三角形斜边的一半.故得答案10或8.40°10或811. (2013年广州市)如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为 ,求点P的坐标.?解:过点P作PD⊥x轴于点D,连接OP,
∵A(6,0),PD⊥OA, ∴OD= OA=3,
在Rt△OPD中, ∵OP= ,OD=3,
∴ ,
∴P(3,2).三、解答题???第26课时 圆的基本性质课时作业 12.如图, AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,求CD的长.解:∵OC⊥AP,OD⊥PB,
∴由垂径定理得:AC=PC,PD=BD,
∴CD是△APB的中位线,
∴CD= AB= ×8=4.13. (2013陕西)如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=8,求OP的长。解:连接OB,过O作OF⊥CD于点 ,作OE⊥AB于点E,
则:BE= AB= ×8=4,
在Rt△OEB中,由勾股定理可得:
,
∵AB=CD
∴OE=OF
∵∠OEP=∠FPE=∠PEO
∴四边形OEPF为正方形
∴OP= OE= . ???????第26课时 圆的基本性质课时作业 14.如图,AB是半圆O的直径,C、D是半圆O上的两点,且OD∥BC,OD与AC交于点E.
(1)若∠B=70°,求∠CAD的度数;
(2)若AB=4,AC=3,求DE的长.解:(1)∵AB是半圆O的直径,∴∠ACB=90°,
又∵OD∥BC,∴∠AEO=90°,
即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°.
∵OA=OD,∴∠DAO=∠ADO= =55°
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;(2)在直角△ABC中,BC= .
∵OE⊥AC,∴AE=EC,
又∵OA=OB,∴OE= BC= .
又∵OD= AB=2,∴DE=OD﹣OE=2﹣ .??????结束谢谢!
同课章节目录
