广东省2015中考数学冲刺复习课件:第25课时 特殊平行四边形(共13张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第25课时 特殊平行四边形(共13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 586.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:10:32 | ||
图片预览




文档简介
课件13张PPT。数学
第25课时 特殊平行四边形第25课时 特殊平行四边形知识考点?对应精练
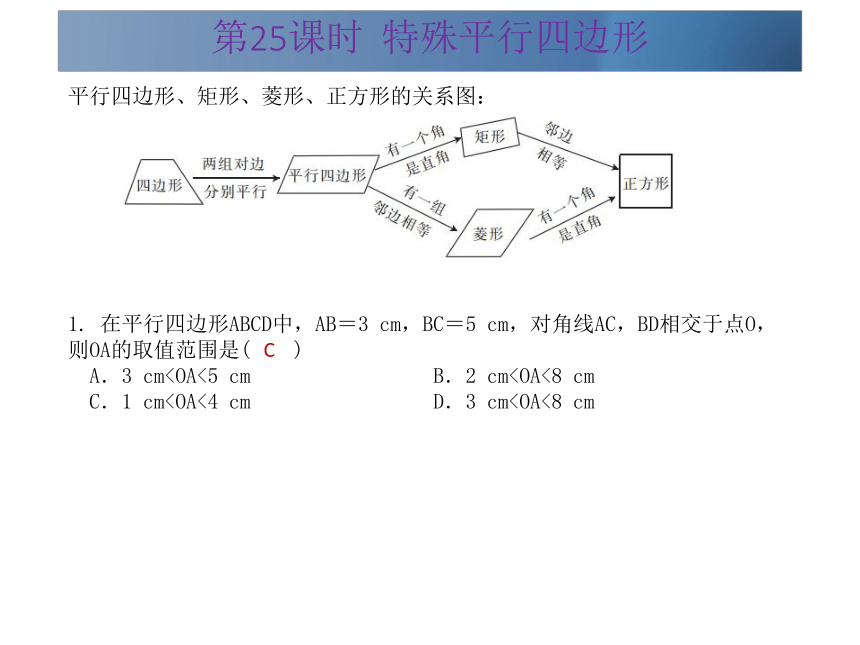
考点分类 矩形、菱形、正方形的定义、性质和判定第25课时 特殊平行四边形平行四边形、矩形、菱形、正方形的关系图:1. 在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.3 cm C.1 cm∵M为AD的中点,∴AM=DM,
在△ABM和△DCM中,
,∴△ABM≌△DCM(SAS).2.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB:AD= 时,四边形MENF是正方形.?(2)解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD, ∴AB=AM=DM=DC,
∵∠A=∠D=90°, ∴∠ABM=∠AMB=∠DMC=∠DCM=45°, ∴∠BMC=90°,
∵四边形ABCD是正方形, ∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°, ∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形, 即当AB:AD=1:2时,四边形MENF是正方形.第25课时 特殊平行四边形真题演练?层层推进
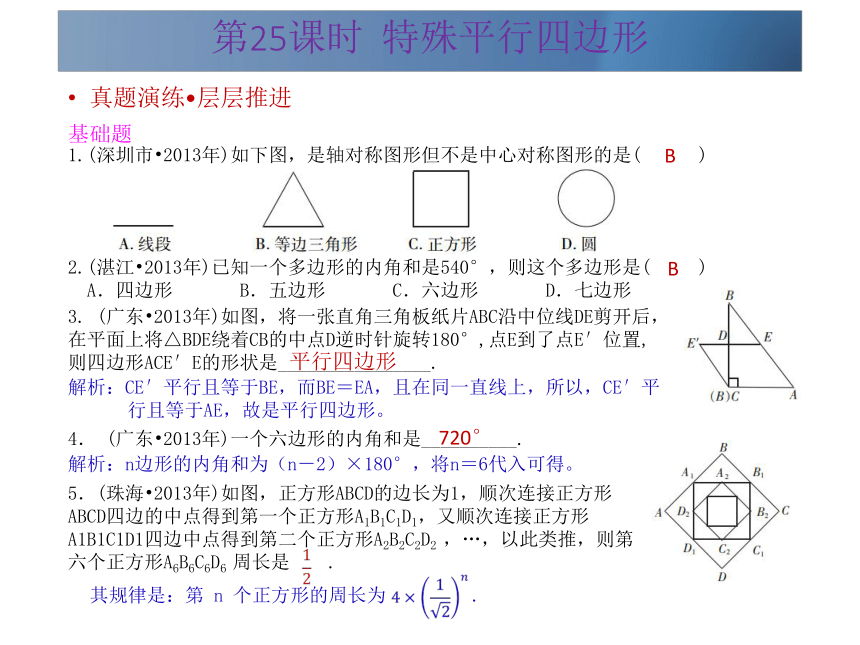
基础题1.(深圳市?2013年)如下图,是轴对称图形但不是中心对称图形的是( )2.(湛江?2013年)已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形B3. (广东?2013年)如图,将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置, 则四边形ACE′E的形状是________________.解析:CE′平行且等于BE,而BE=EA,且在同一直线上,所以,CE′平行且等于AE,故是平行四边形。B平行四边形4. (广东?2013年)一个六边形的内角和是__________.解析:n边形的内角和为(n-2)×180°,将n=6代入可得。5.(珠海?2013年)如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,又顺次连接正方形A1B1C1D1四边中点得到第二个正方形A2B2C2D2 ,…,以此类推,则第六个正方形A6B6C6D6 周长是 . 其规律是:第 n 个正方形的周长为 .720°??第25课时 特殊平行四边形提高题6. (2013年广州市)如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.解:∵四边形ABCD是菱形,对角线AC与BD相交于O,
∴AC⊥BD,DO=BO,
∵AB=5,AO=4,
∴BO= =3,
∴BD=2BO=2×3=6.?7. (广东?2014年) 如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.证明:(1)在□ABCD中,AB∥CD,∴∠CFE=∠ABF ∠A=∠ADF
∵AE=ED,∴△ABE≌△EFD ∴FD=AB.
(2)∵平行四边形ABCD,∴AD=BC=2ED,
∵AD∥BC ∴△EFD∽△FBC
∴ S△EFD:S△FBC =1:4 ∴S△EFD:S四边形ABCD =1:5
∴S△EFD =1.6 第25课时 特殊平行四边形拔高题8.(2014?深圳)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,
在△ADB与△CDB中, ,
∴△ADB≌△CDB(SSS) ∴∠BCD=∠BAD,
∵∠BCD=∠ADF, ∴∠BAD=∠ADF , ∴AB∥FD,
∵BD⊥AC,AF⊥AC, ∴AF∥BD,
∴四边形ABDF是平行四边形,????(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴四边形ABDF是菱形, ∴AB=BD=5,
∵AD=6,设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2, 即52﹣x2=62﹣(5﹣x)2
解得:x= , ∴ ,
∴AC=2AE= .第25课时 特殊平行四边形课时作业一、选择题1.(2014广东)在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.2.(2014广东)一个多边形的内角和是900°,这个多边形的边数是( )
A.10 B.9 C.8 D.73.(2014年广东) 如图,□ABCD中,下列说法一定正确的是( )
A.AC=BD B.AC⊥BD C.AB=CD D.AB=BC 4. 若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A.矩形 B.等腰梯形
C.对角线相等的四边形 D.对角线互相垂直的四边形CDCC第25课时 特殊平行四边形课时作业 5.(2014广州市)将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图2-①,测得AC=2 ,当∠B=60°时,如图2-②,AC=( ).
(A) (B)2 (C) (D) 图2-①图2-②A???6. 矩形两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的长为 cm.二、填空题7. (2014?珠海)边长为3cm的菱形的周长是 。 8.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD 从中任选两个条件,写出能使四边形ABCD为平行四边形的选法是 (只需要写出一种即可).
9. 如图,在菱形ABCD中,CE⊥AD,垂足为E,如果AE=DE.则∠A= ,∠B= 。512cm在这四种任写一个就行①④;①③;③④;①②120°60°第25课时 特殊平行四边形课时作业 10. (2013山西)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点
A′处,则AE的长为______.?三、解答题解:由勾股定理求得:BD=13,
DA=D A′=BC=5,∠D A′E=∠DAE=90°,
设AE=x,则A′E=x,BE=12-x,B A′=13-5=8,
在Rt△E B中,(12-x)2=x2+82,解得:x= ,即AE的长为 . ??11、(广东卷?2013).如图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结AE,交CD于点F,
求证:△AFD≌△EFC.解:(1)如图所示,线段CE为所求;
(2)证明:在□ABCD中,
AD∥BC,AD=BC.∴∠CEF=∠DAF
∵CE=BC,∴AD=CE,
又∵∠CFE=∠DFA,∴△AFD≌△EFC.第25课时 特殊平行四边形课时作业 12、(2014年广州市)如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别交于点E、F,
求证:△AOE≌△COF.证明:∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AO=CO,AB∥CD, ∴∠EAO=∠FCO,
在△AOE和△COF中, ,
∴△AOE≌△COF.?13. (2014?梅州)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?(1)证明:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.
(2)解:GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF, ∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC, ∴△ECG≌△FCG(SAS).
∴GE=GF. ∴GE=DF+GD=BE+GD.第25课时 特殊平行四边形课时作业 14. (广东梅州?2013年) 如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)若四边形BECF为正方形,求∠A的度数.解:(1)证明:∵BC的垂直平分线EF交于点D,
∴BF=FC,BE=EC.
又∵∠ACB=90°,
∴EF//AC.
∴BE:AB=DB:BC,
∵D为BC中点,
∴DB:BC=1:2,
∴BE:AB=1:2,
∴E为AB中点,即BE=AE,
∵CF=AE,∴CF=BE,∴CF=FB=BE=CE,
∴四边形BECF是菱形.
(2)如图,∵四边形BECF为正方形,
∴∠BEC=90°.
又AE=CE,∴∠A=45°.结束谢谢!
考点分类 矩形、菱形、正方形的定义、性质和判定第25课时 特殊平行四边形平行四边形、矩形、菱形、正方形的关系图:1. 在平行四边形ABCD中,AB=3 cm,BC=5 cm,对角线AC,BD相交于点O,则OA的取值范围是( )
A.3 cm
在△ABM和△DCM中,
,∴△ABM≌△DCM(SAS).2.已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点.
(1)求证:△ABM≌△DCM;
(2)填空:当AB:AD= 时,四边形MENF是正方形.?(2)解:当AB:AD=1:2时,四边形MENF是正方形,
理由是:∵AB:AD=1:2,AM=DM,AB=CD, ∴AB=AM=DM=DC,
∵∠A=∠D=90°, ∴∠ABM=∠AMB=∠DMC=∠DCM=45°, ∴∠BMC=90°,
∵四边形ABCD是正方形, ∴∠ABC=∠DCB=90°,
∴∠MBC=∠MCB=45°, ∴BM=CM,
∵N、E、F分别是BC、BM、CM的中点,
∴BE=CF,ME=MF,NF∥BM,NE∥CM,
∴四边形MENF是平行四边形,
∵ME=MF,∠BMC=90°,
∴四边形MENF是正方形, 即当AB:AD=1:2时,四边形MENF是正方形.第25课时 特殊平行四边形真题演练?层层推进
基础题1.(深圳市?2013年)如下图,是轴对称图形但不是中心对称图形的是( )2.(湛江?2013年)已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形B3. (广东?2013年)如图,将一张直角三角板纸片ABC沿中位线DE剪开后,在平面上将△BDE绕着CB的中点D逆时针旋转180°,点E到了点E′位置, 则四边形ACE′E的形状是________________.解析:CE′平行且等于BE,而BE=EA,且在同一直线上,所以,CE′平行且等于AE,故是平行四边形。B平行四边形4. (广东?2013年)一个六边形的内角和是__________.解析:n边形的内角和为(n-2)×180°,将n=6代入可得。5.(珠海?2013年)如图,正方形ABCD的边长为1,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1,又顺次连接正方形A1B1C1D1四边中点得到第二个正方形A2B2C2D2 ,…,以此类推,则第六个正方形A6B6C6D6 周长是 . 其规律是:第 n 个正方形的周长为 .720°??第25课时 特殊平行四边形提高题6. (2013年广州市)如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.解:∵四边形ABCD是菱形,对角线AC与BD相交于O,
∴AC⊥BD,DO=BO,
∵AB=5,AO=4,
∴BO= =3,
∴BD=2BO=2×3=6.?7. (广东?2014年) 如图,在平行四边形ABCD中,E是AD边上的中点,连接BE,并延长BE交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.证明:(1)在□ABCD中,AB∥CD,∴∠CFE=∠ABF ∠A=∠ADF
∵AE=ED,∴△ABE≌△EFD ∴FD=AB.
(2)∵平行四边形ABCD,∴AD=BC=2ED,
∵AD∥BC ∴△EFD∽△FBC
∴ S△EFD:S△FBC =1:4 ∴S△EFD:S四边形ABCD =1:5
∴S△EFD =1.6 第25课时 特殊平行四边形拔高题8.(2014?深圳)已知BD垂直平分AC,∠BCD=∠ADF,AF⊥AC
(1)证明ABDF是平行四边形;
(2)若AF=DF=5,AD=6,求AC的长.(1)证明:∵BD垂直平分AC,∴AB=BC,AD=DC,
在△ADB与△CDB中, ,
∴△ADB≌△CDB(SSS) ∴∠BCD=∠BAD,
∵∠BCD=∠ADF, ∴∠BAD=∠ADF , ∴AB∥FD,
∵BD⊥AC,AF⊥AC, ∴AF∥BD,
∴四边形ABDF是平行四边形,????(2)解:∵四边形ABDF是平行四边形,AF=DF=5,
∴四边形ABDF是菱形, ∴AB=BD=5,
∵AD=6,设BE=x,则DE=5﹣x,
∴AB2﹣BE2=AD2﹣DE2, 即52﹣x2=62﹣(5﹣x)2
解得:x= , ∴ ,
∴AC=2AE= .第25课时 特殊平行四边形课时作业一、选择题1.(2014广东)在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )
A. B. C. D.2.(2014广东)一个多边形的内角和是900°,这个多边形的边数是( )
A.10 B.9 C.8 D.73.(2014年广东) 如图,□ABCD中,下列说法一定正确的是( )
A.AC=BD B.AC⊥BD C.AB=CD D.AB=BC 4. 若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A.矩形 B.等腰梯形
C.对角线相等的四边形 D.对角线互相垂直的四边形CDCC第25课时 特殊平行四边形课时作业 5.(2014广州市)将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变,当∠B=90°时,如图2-①,测得AC=2 ,当∠B=60°时,如图2-②,AC=( ).
(A) (B)2 (C) (D) 图2-①图2-②A???6. 矩形两条对角线的夹角为60°,一条对角线与短边的和为15cm,则短边的长为 cm.二、填空题7. (2014?珠海)边长为3cm的菱形的周长是 。 8.四边形ABCD中,对角线AC、BD相交于点O,给出下列四个条件:
①AD∥BC;②AD=BC;③OA=OC;④OB=OD 从中任选两个条件,写出能使四边形ABCD为平行四边形的选法是 (只需要写出一种即可).
9. 如图,在菱形ABCD中,CE⊥AD,垂足为E,如果AE=DE.则∠A= ,∠B= 。512cm在这四种任写一个就行①④;①③;③④;①②120°60°第25课时 特殊平行四边形课时作业 10. (2013山西)如图,在矩形纸片ABCD中,AB=12,BC=5,点E在AB上,将△DAE沿DE折叠,使点A落在对角线BD上的点
A′处,则AE的长为______.?三、解答题解:由勾股定理求得:BD=13,
DA=D A′=BC=5,∠D A′E=∠DAE=90°,
设AE=x,则A′E=x,BE=12-x,B A′=13-5=8,
在Rt△E B中,(12-x)2=x2+82,解得:x= ,即AE的长为 . ??11、(广东卷?2013).如图,已知□ABCD.
(1)作图:延长BC,并在BC的延长线上截取线段CE,使得CE=BC(用尺规作图法,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连结AE,交CD于点F,
求证:△AFD≌△EFC.解:(1)如图所示,线段CE为所求;
(2)证明:在□ABCD中,
AD∥BC,AD=BC.∴∠CEF=∠DAF
∵CE=BC,∴AD=CE,
又∵∠CFE=∠DFA,∴△AFD≌△EFC.第25课时 特殊平行四边形课时作业 12、(2014年广州市)如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别交于点E、F,
求证:△AOE≌△COF.证明:∵平行四边形ABCD的对角线AC、BD相交于点O,
∴AO=CO,AB∥CD, ∴∠EAO=∠FCO,
在△AOE和△COF中, ,
∴△AOE≌△COF.?13. (2014?梅州)如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?(1)证明:在正方形ABCD中,
∵BC=CD,∠B=∠CDF,BE=DF,∴△CBE≌△CDF(SAS).∴CE=CF.
(2)解:GE=BE+GD成立.
理由是:∵由(1)得:△CBE≌△CDF, ∴∠BCE=∠DCF,
∴∠BCE+∠ECD=∠DCF+∠ECD,即∠ECF=∠BCD=90°,
又∵∠GCE=45°,∴∠GCF=∠GCE=45°.
∵CE=CF,∠GCE=∠GCF,GC=GC, ∴△ECG≌△FCG(SAS).
∴GE=GF. ∴GE=DF+GD=BE+GD.第25课时 特殊平行四边形课时作业 14. (广东梅州?2013年) 如图,在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交于点D,交AB于点E,且CF=AE.
(1)求证:四边形BECF是菱形;
(2)若四边形BECF为正方形,求∠A的度数.解:(1)证明:∵BC的垂直平分线EF交于点D,
∴BF=FC,BE=EC.
又∵∠ACB=90°,
∴EF//AC.
∴BE:AB=DB:BC,
∵D为BC中点,
∴DB:BC=1:2,
∴BE:AB=1:2,
∴E为AB中点,即BE=AE,
∵CF=AE,∴CF=BE,∴CF=FB=BE=CE,
∴四边形BECF是菱形.
(2)如图,∵四边形BECF为正方形,
∴∠BEC=90°.
又AE=CE,∴∠A=45°.结束谢谢!
同课章节目录
