广东省2015中考数学冲刺复习课件:第20课时 等腰三角形与等边三角形(共16张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第20课时 等腰三角形与等边三角形(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 852.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:14:30 | ||
图片预览






文档简介
课件16张PPT。数学
第20课时 等腰三角形与等边三角形第20课时 等腰三角形与等边三角形知识考点?对应精练
考点分类一 三角形的性质1.三角形的任意两边之和大于第三边,任意两边之差小于第三边.2.三角形的内角和是180°;三角形的外角等于与它不相邻的两个内角的和,三角形的外角大于任何一个和它不相邻的内角.1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形的个数为( )
A.2 B.3 C.5 D.132.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是( )
A.61° B.60°
C.37° D.39°BC第20课时 等腰三角形与等边三角形考点分类二 等腰三角形的性质与判定1.概念:有两条边相等的三角形叫等腰三角形;有三条边都相等的三角形叫做等边三角形(也叫正三角形).2.等腰三角形的性质
(1)等腰三角形的两腰相等;等腰三角形的两个底角相等;
(2)等腰三角形的顶角角平分线、底边上的中线和高互相重合,简称“三线合一”;
(3)等腰三角形是轴对称图形1. 如果等腰三角形的两边长是6 cm和3 cm,那么它的周长是( )
A.9 cm B.12 cm
C.15 cm或12 cm D.15 cm2. 如图,在等腰⊿ABC中,分别求出它们的底角的度数。DB3.等腰三角形的判定
(1)有两条边相等的三角形是等腰三角形;(2)有两个内角相等的三角形是等腰三角形.3. 下面给出的几种三角形:(1)有两个角为60°的三角形;(2)三个外角都相等的三角形;(3)一边上的高也是这边上的中线的等腰三角形;(4)有一个角为60°的等腰三角形.其中一定是等边三角形的有( )
A.4个 B.3个 C.2个 D.1个解:∵AB=AC,∠A=120°,∴∠B=∠C=30°.第20课时 等腰三角形与等边三角形考点分类三 直角三角形的性质与判定1、性质
(1)直角三角形的两个锐角互余;
(2)勾股定理:a2+b2=c2(在Rt△ABC中,∠C=90°);
(3)在直角三角形中,如果有一个锐角等于 30°,那么它所对的直角边等于斜边的一半;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角为 30°;
(5)直角三角形斜边上的中线等于斜边的一半.
2.判定
(1)勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形;
(2)如果一个三角形一边上的中线等于这边的一半,那么这个三角形为直角三角形;1. 在△ABC中,∠C=90°,若AC=6,CB=8,则AB上的高为 .2. 在下列以线段a、b、c的长为三边的三角形中,不能构成直角三角形的是( )
A. a=9,b=41,c=40 B. a=b=5,c=5
C. a︰b︰c=3︰4︰5 D. a=11,b=12,c=15?D?第20课时 等腰三角形与等边三角形考点分类四 三角形中位线定理:三角形的中位线,平行于第三边,并且等于第三边的一半。1. (2012浙江台州)如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
A.5 B.10 C.20 D.402、顺次连结四边形的各边中点的四边形是 四边形。平行C考点分类五 三角形全等证明三角形全等有方法有:SSS、SAS、ASA、AAS。对于直角三角形,还有HL.2. (2013?深圳市)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是( )
A. B. C. D. 1. (2014?漳州)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)????解:AC=DF.
证明:∵BF=EC,∴BF-CF=EC-CF,∴BC=EF,
在△ABC和△DEF中, ,∴△ABC≌△DEF(SAS).C第20课时 等腰三角形与等边三角形考点分类六 相似三角形的判定与性质1、判定方法:
①平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似;
②.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;
③.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;
④.如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
对于直角三角形相似的判定定理还有:斜边与一条直角边对应成比例的两直角三角形相似。
2、相似三角形的性质:
①.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比。
②.相似三角形周长的比等于相似比。
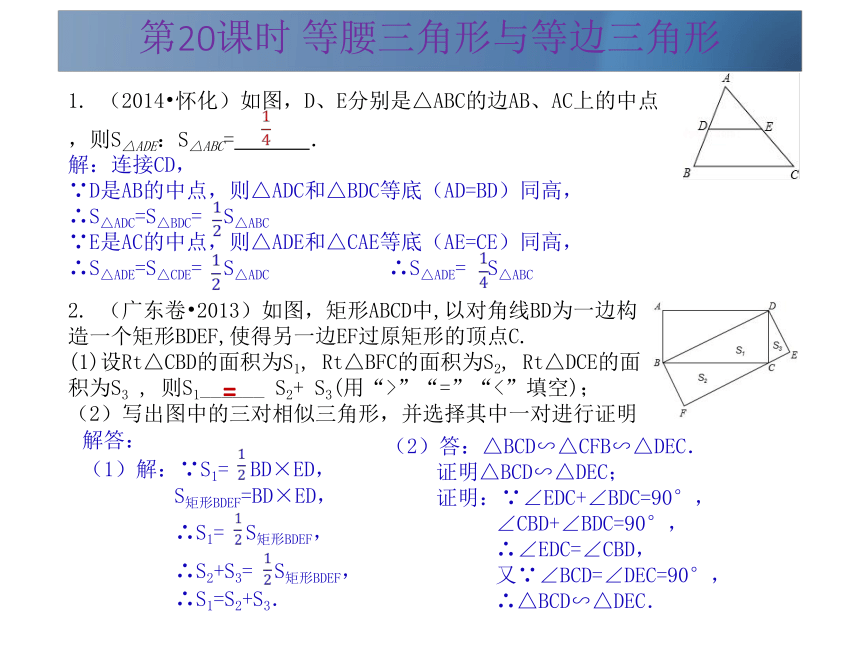
③.相似三角形面积的比等于相似比的平方。第20课时 等腰三角形与等边三角形 1. (2014?怀化)如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:S△ABC= .2. (广东卷?2013)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1, Rt△BFC的面积为S2, Rt△DCE的面积为S3 , 则S1______ S2+ S3(用“>”“=”“<”填空);
(2)写出图中的三对相似三角形,并选择其中一对进行证明解答:
(1)解:∵S1= BD×ED,
S矩形BDEF=BD×ED,
∴S1= S矩形BDEF,
∴S2+S3= S矩形BDEF,
∴S1=S2+S3.解:连接CD,
∵D是AB的中点,则△ADC和△BDC等底(AD=BD)同高,
∴S△ADC=S△BDC= S△ABC
∵E是AC的中点,则△ADE和△CAE等底(AE=CE)同高,
∴S△ADE=S△CDE= S△ADC ∴S△ADE= S△ABC??????=?(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,
∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC. 第20课时 等腰三角形与等边三角形真题演练?层层推进
基础题1. (广东省?2012年) 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A、5 B、6 C、11 D、163. (广东梅州?2013年) 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是 .2. (广东佛山?2013年) 如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m)( )
A.34.64m B.34.6m C.28.3m D.17.3mCB??第20课时 等腰三角形与等边三角形 4、 (广东湛江?2013年) 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.5、(广东珠海?2013年) (全等三角形) 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.证明:∵FB=CE.
∴BC=CF.
∵AB∥ED.
∴∠B=∠E.
∵AC∥DF.
∴∠ACB=∠DEF
∴△ABC≌△DEF
∴AC=DF证明:∵∠BCE=∠DCA
∴∠BCE+∠ACE=∠DCA+∠ACE, 即∠BCA=∠DCE
∴AC=EC.
∴∠A=∠E
∴ △BCA≌△DCE(ASA)
∴BC=DC第20课时 等腰三角形与等边三角形提高题6. (广东佛山市?2013年) (相似三角形)网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.?7. (深圳市?2013年) 如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,求所得四边形的周长.解:如图,BC=2,DE=1,AB=4,AC=2 ,
(1)AE与EC重合时,周长为8;
(2)AD与BD重合时,周长为4+2 ,
所以,四边形的周长是8或4+2 .???第20课时 等腰三角形与等边三角形拔高题8. (广东珠海?2013年)如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP; (2)求证:AE=CP;
(3)当 ,BP′=5 时,求线段AB的长.????????第20课时 等腰三角形与等边三角形课时作业一、选择题1.(2014?广东卷)一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17 B.15 C.13 D.13或172. (2012年?海南省)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm3. (2012?广东深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则么∠1+∠2的度数为( )
A. 120° B. 180° C. 240° D. 300°4. 三角形的下列线段中,能将三角形的面积分成相等两部分的是( )
A. 中线 B. 角平分线 C. 高 D. 中位线5.(2014?深圳)如图,△ABC和△DEF中,AB=DE、角∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F ∵AB=DE,∠B=∠DEF,
∴添加AC∥DF,得出∠ACB=∠F,即可证明△ABC≌△DEF,故A、D正确;
当添加∠A=∠D时,根据ASA,也可证明△ABC≌△DEF,故B正确;
但添加AC=DF时,没有SSA定理,不能证明△ABC≌△DEF,故C不正确;
故选C.AACCC第20课时 等腰三角形与等边三角形课时作业二、填空题6. (2014广州市)△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是___ __.8. (2014广东卷)如图,在△ABC中,点D,E分别是AB,AC的中点,若BC=6,则DE= ;7.(2014广州市)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题:____ _____,该逆命题是____命题(填“真”或“假”).如果两个三角形的面积相等,那么这两个三角形全等假140°9.(2014年梅州) 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C′,A′B′交AC于点D,若∠ADC=90°,则∠A= . 10.(2014年广东卷)如图,△ABC绕点A顺时针旋转45°得到△A′B′C′ ,若∠BAC=90°,AB=AC= ,则图中阴影部分的面积等于 . ??55°3解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,
∴∠ACA′=35°,则∠A′=90°﹣35°=55°,则∠A=∠A′=55°.第20课时 等腰三角形与等边三角形课时作业三、解答题11. 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,求∠1的度数.解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.故答案为:75. 12. (2014?绍兴)课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题:如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算. ?第20课时 等腰三角形与等边三角形课时作业 13. (2014?黄冈)已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.证明:连接AD,在△ACD和△ABD中,
, ∴△ACD≌△ABD(SSS), ∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF, ∴DE=DF.?14. (2014?怀化)如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的角平分线.求证:
(1)△ABE≌△AFE; (2)∠FAD=∠CDE.证明:(1)∵EA是∠BEF的角平分线, ∴∠1=∠2,
在△ABE和△AFE中,
,∴△ABE≌△AFE(AAS);
(2)∵△ABE≌△AFE, ∴AB=AF,
∵四边形ABCD平行四边形, ∴AB=CD,AD∥CB,AB∥CD,
∴AF=CD,∠ADF=∠DEC,∠B+∠C=180°,
∵∠B=∠AFE,∠AFE+∠AFD=180°, ∴∠AFD=∠C,
在△AFD和△DCE中,
, ∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
??结束谢谢!
考点分类一 三角形的性质1.三角形的任意两边之和大于第三边,任意两边之差小于第三边.2.三角形的内角和是180°;三角形的外角等于与它不相邻的两个内角的和,三角形的外角大于任何一个和它不相邻的内角.1.已知三角形三边长分别为2,x,13,若x为正整数,则这样的三角形的个数为( )
A.2 B.3 C.5 D.132.如图,∠BDC=98°,∠C=38°,∠B=23°,∠A的度数是( )
A.61° B.60°
C.37° D.39°BC第20课时 等腰三角形与等边三角形考点分类二 等腰三角形的性质与判定1.概念:有两条边相等的三角形叫等腰三角形;有三条边都相等的三角形叫做等边三角形(也叫正三角形).2.等腰三角形的性质
(1)等腰三角形的两腰相等;等腰三角形的两个底角相等;
(2)等腰三角形的顶角角平分线、底边上的中线和高互相重合,简称“三线合一”;
(3)等腰三角形是轴对称图形1. 如果等腰三角形的两边长是6 cm和3 cm,那么它的周长是( )
A.9 cm B.12 cm
C.15 cm或12 cm D.15 cm2. 如图,在等腰⊿ABC中,分别求出它们的底角的度数。DB3.等腰三角形的判定
(1)有两条边相等的三角形是等腰三角形;(2)有两个内角相等的三角形是等腰三角形.3. 下面给出的几种三角形:(1)有两个角为60°的三角形;(2)三个外角都相等的三角形;(3)一边上的高也是这边上的中线的等腰三角形;(4)有一个角为60°的等腰三角形.其中一定是等边三角形的有( )
A.4个 B.3个 C.2个 D.1个解:∵AB=AC,∠A=120°,∴∠B=∠C=30°.第20课时 等腰三角形与等边三角形考点分类三 直角三角形的性质与判定1、性质
(1)直角三角形的两个锐角互余;
(2)勾股定理:a2+b2=c2(在Rt△ABC中,∠C=90°);
(3)在直角三角形中,如果有一个锐角等于 30°,那么它所对的直角边等于斜边的一半;
(4)在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角为 30°;
(5)直角三角形斜边上的中线等于斜边的一半.
2.判定
(1)勾股定理的逆定理:如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形;
(2)如果一个三角形一边上的中线等于这边的一半,那么这个三角形为直角三角形;1. 在△ABC中,∠C=90°,若AC=6,CB=8,则AB上的高为 .2. 在下列以线段a、b、c的长为三边的三角形中,不能构成直角三角形的是( )
A. a=9,b=41,c=40 B. a=b=5,c=5
C. a︰b︰c=3︰4︰5 D. a=11,b=12,c=15?D?第20课时 等腰三角形与等边三角形考点分类四 三角形中位线定理:三角形的中位线,平行于第三边,并且等于第三边的一半。1. (2012浙江台州)如图,点D、E、F分别为∠ABC三边的中点,若△DEF的周长为10,则△ABC的周长为( )
A.5 B.10 C.20 D.402、顺次连结四边形的各边中点的四边形是 四边形。平行C考点分类五 三角形全等证明三角形全等有方法有:SSS、SAS、ASA、AAS。对于直角三角形,还有HL.2. (2013?深圳市)如图,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个项点分别在这三条平行直线上,则sinα的值是( )
A. B. C. D. 1. (2014?漳州)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)????解:AC=DF.
证明:∵BF=EC,∴BF-CF=EC-CF,∴BC=EF,
在△ABC和△DEF中, ,∴△ABC≌△DEF(SAS).C第20课时 等腰三角形与等边三角形考点分类六 相似三角形的判定与性质1、判定方法:
①平行于三角形一边的直线(或两边的延长线)和其他两边相交,所构成的三角形与原三角形相似;
②.如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似;
③.如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似;
④.如果两个三角形的三组对应边的比相等,那么这两个三角形相似;
对于直角三角形相似的判定定理还有:斜边与一条直角边对应成比例的两直角三角形相似。
2、相似三角形的性质:
①.相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比。
②.相似三角形周长的比等于相似比。
③.相似三角形面积的比等于相似比的平方。第20课时 等腰三角形与等边三角形 1. (2014?怀化)如图,D、E分别是△ABC的边AB、AC上的中点,则S△ADE:S△ABC= .2. (广东卷?2013)如图,矩形ABCD中,以对角线BD为一边构造一个矩形BDEF,使得另一边EF过原矩形的顶点C.
(1)设Rt△CBD的面积为S1, Rt△BFC的面积为S2, Rt△DCE的面积为S3 , 则S1______ S2+ S3(用“>”“=”“<”填空);
(2)写出图中的三对相似三角形,并选择其中一对进行证明解答:
(1)解:∵S1= BD×ED,
S矩形BDEF=BD×ED,
∴S1= S矩形BDEF,
∴S2+S3= S矩形BDEF,
∴S1=S2+S3.解:连接CD,
∵D是AB的中点,则△ADC和△BDC等底(AD=BD)同高,
∴S△ADC=S△BDC= S△ABC
∵E是AC的中点,则△ADE和△CAE等底(AE=CE)同高,
∴S△ADE=S△CDE= S△ADC ∴S△ADE= S△ABC??????=?(2)答:△BCD∽△CFB∽△DEC.
证明△BCD∽△DEC;
证明:∵∠EDC+∠BDC=90°,
∠CBD+∠BDC=90°,
∴∠EDC=∠CBD,
又∵∠BCD=∠DEC=90°,
∴△BCD∽△DEC. 第20课时 等腰三角形与等边三角形真题演练?层层推进
基础题1. (广东省?2012年) 已知三角形两边的长分别是4和10,则此三角形第三边的长可能是( )
A、5 B、6 C、11 D、163. (广东梅州?2013年) 如图,已知△ABC是腰长为1的等腰直角三角形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是 .2. (广东佛山?2013年) 如图,若∠A=60°,AC=20m,则BC大约是(结果精确到0.1m)( )
A.34.64m B.34.6m C.28.3m D.17.3mCB??第20课时 等腰三角形与等边三角形 4、 (广东湛江?2013年) 如图,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AC=DF.5、(广东珠海?2013年) (全等三角形) 如图,已知,EC=AC,∠BCE=∠DCA,∠A=∠E,求证:BC=DC.证明:∵FB=CE.
∴BC=CF.
∵AB∥ED.
∴∠B=∠E.
∵AC∥DF.
∴∠ACB=∠DEF
∴△ABC≌△DEF
∴AC=DF证明:∵∠BCE=∠DCA
∴∠BCE+∠ACE=∠DCA+∠ACE, 即∠BCA=∠DCE
∴AC=EC.
∴∠A=∠E
∴ △BCA≌△DCE(ASA)
∴BC=DC第20课时 等腰三角形与等边三角形提高题6. (广东佛山市?2013年) (相似三角形)网格图中每个方格都是边长为1的正方形.若A,B,C,D,E,F都是格点,试说明△ABC∽△DEF.?7. (深圳市?2013年) 如图,有一张一个角为30°,最小边长为2的直角三角形纸片,沿图中所示的中位线剪开后,将两部分拼成一个四边形,求所得四边形的周长.解:如图,BC=2,DE=1,AB=4,AC=2 ,
(1)AE与EC重合时,周长为8;
(2)AD与BD重合时,周长为4+2 ,
所以,四边形的周长是8或4+2 .???第20课时 等腰三角形与等边三角形拔高题8. (广东珠海?2013年)如图,在Rt△ABC中,∠C=90°,点P为AC边上的一点,将线段AP绕点A顺时针方向旋转(点P对应点P′),当AP旋转至AP′⊥AB时,点B、P、P′恰好在同一直线上,此时作P′E⊥AC于点E.
(1)求证:∠CBP=∠ABP; (2)求证:AE=CP;
(3)当 ,BP′=5 时,求线段AB的长.????????第20课时 等腰三角形与等边三角形课时作业一、选择题1.(2014?广东卷)一个等腰三角形的两边长分别是3和7,则它的周长为( )
A.17 B.15 C.13 D.13或172. (2012年?海南省)一个三角形的两边长分别为3cm和7cm,则此三角形的第三边的长可能是( )
A.3cm B.4cm C.7cm D.11cm3. (2012?广东深圳)如图所示,一个60°角的三角形纸片,剪去这个60°角后,得到一个四边形,则么∠1+∠2的度数为( )
A. 120° B. 180° C. 240° D. 300°4. 三角形的下列线段中,能将三角形的面积分成相等两部分的是( )
A. 中线 B. 角平分线 C. 高 D. 中位线5.(2014?深圳)如图,△ABC和△DEF中,AB=DE、角∠B=∠DEF,添加下列哪一个条件无法证明△ABC≌△DEF( )
A、AC∥DF B、∠A=∠D C、AC=DF D、∠ACB=∠F ∵AB=DE,∠B=∠DEF,
∴添加AC∥DF,得出∠ACB=∠F,即可证明△ABC≌△DEF,故A、D正确;
当添加∠A=∠D时,根据ASA,也可证明△ABC≌△DEF,故B正确;
但添加AC=DF时,没有SSA定理,不能证明△ABC≌△DEF,故C不正确;
故选C.AACCC第20课时 等腰三角形与等边三角形课时作业二、填空题6. (2014广州市)△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是___ __.8. (2014广东卷)如图,在△ABC中,点D,E分别是AB,AC的中点,若BC=6,则DE= ;7.(2014广州市)已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题:____ _____,该逆命题是____命题(填“真”或“假”).如果两个三角形的面积相等,那么这两个三角形全等假140°9.(2014年梅州) 如图,把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C′,A′B′交AC于点D,若∠ADC=90°,则∠A= . 10.(2014年广东卷)如图,△ABC绕点A顺时针旋转45°得到△A′B′C′ ,若∠BAC=90°,AB=AC= ,则图中阴影部分的面积等于 . ??55°3解:∵把△ABC绕点C按顺时针方向旋转35°,得到△A′B′C,A′B′交AC于点D,∠A′DC=90°,
∴∠ACA′=35°,则∠A′=90°﹣35°=55°,则∠A=∠A′=55°.第20课时 等腰三角形与等边三角形课时作业三、解答题11. 将一副直角三角板如图放置,使含30°角的三角板的直角边和含45°角的三角板的一条直角边重合,求∠1的度数.解:如图.∵∠3=60°,∠4=45°,∴∠1=∠5=180°﹣∠3﹣∠4=75°.故答案为:75. 12. (2014?绍兴)课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题:如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算. ?第20课时 等腰三角形与等边三角形课时作业 13. (2014?黄冈)已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.证明:连接AD,在△ACD和△ABD中,
, ∴△ACD≌△ABD(SSS), ∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF, ∴DE=DF.?14. (2014?怀化)如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的角平分线.求证:
(1)△ABE≌△AFE; (2)∠FAD=∠CDE.证明:(1)∵EA是∠BEF的角平分线, ∴∠1=∠2,
在△ABE和△AFE中,
,∴△ABE≌△AFE(AAS);
(2)∵△ABE≌△AFE, ∴AB=AF,
∵四边形ABCD平行四边形, ∴AB=CD,AD∥CB,AB∥CD,
∴AF=CD,∠ADF=∠DEC,∠B+∠C=180°,
∵∠B=∠AFE,∠AFE+∠AFD=180°, ∴∠AFD=∠C,
在△AFD和△DCE中,
, ∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
??结束谢谢!
同课章节目录
