广东省2015中考数学冲刺复习课件:第19课时 全等三角形(共16张PPT)
文档属性
| 名称 | 广东省2015中考数学冲刺复习课件:第19课时 全等三角形(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 702.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-03-05 14:15:22 | ||
图片预览





文档简介
课件16张PPT。数学
第19课时 全等三角形第19课时 全等三角形最新广东省初中毕业生数学学科学业考试大纲:①理解三角形有关概念(内角、外角、中线、高、角平分线),会画出任意三角形的角平分线、中线和高,了解三角形的稳定性②掌握三角形中位线的性质.③理解全等三角形的概念,掌握两个三角形全等的条件.④了解等腰三角形的有关概念,掌握等腰三角形的性质和一个三角形是等腰三角形的条件.⑤理解等边三角形的概念及其性质.⑥了解直角三角形的概念,掌握直角三角形的性质和一个三角形是直角三角形的条件.三角形⑦会运用勾股定理解决简单问题;会用勾股定理的逆定理判断直角三角形.⑧了解三角形重心的概念.第19课时 全等三角形知识考点?对应精练
考点分类一 全等三角形的概念与性质 全等三角形:能够完全重合的两个三角形叫做全等三角形.
全等三角形的性质:(1)全等三角形的对应角、对应边分别相等;
(2)全等三角形中的对应线段(角平分线、中线、高)相等、周长相等、面积相等.1.如图19-1所示,已知△ABC≌△BAD,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.10cm B.7 cm C.5 cm D.无法确定提示:根据全等三角形的性质,对应边相等,AC=BD=10cm.2.如图19-2,如果△ABC≌△DCB,AB=10,AC=12,BC=8,则△DCB的周长是( )
A.20 B.30 C.40 D.45提示:根据全等三角形的性质,对应边相等,所以AB=CD=10,AC=BD=12,BC=CB=8,
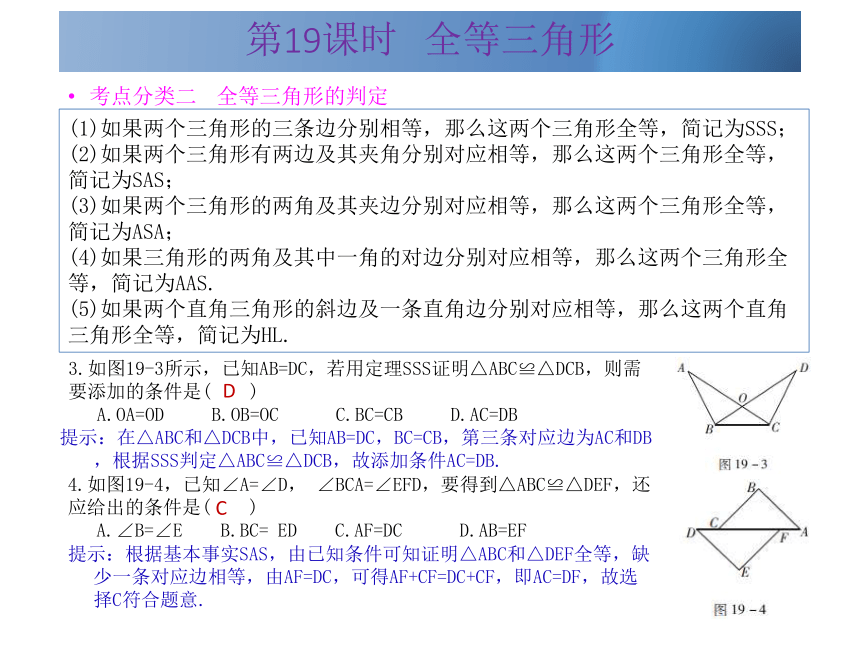
所以△DCB的周长=CD+BD+CB=10+12+8=30.BA第19课时 全等三角形考点分类二 全等三角形的判定(1)如果两个三角形的三条边分别相等,那么这两个三角形全等,简记为SSS;
(2)如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等,简记为SAS;
(3)如果两个三角形的两角及其夹边分别对应相等,那么这两个三角形全等,简记为ASA;
(4)如果三角形的两角及其中一角的对边分别对应相等,那么这两个三角形全等,简记为AAS.
(5)如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等,简记为HL.3.如图19-3所示,已知AB=DC,若用定理SSS证明△ABC≌△DCB,则需要添加的条件是( )
A.OA=OD B.OB=OC C.BC=CB D.AC=DB提示:在△ABC和△DCB中,已知AB=DC,BC=CB,第三条对应边为AC和DB,根据SSS判定△ABC≌△DCB,故添加条件AC=DB.4.如图19-4,已知∠A=∠D, ∠BCA=∠EFD,要得到△ABC≌△DEF,还应给出的条件是( )
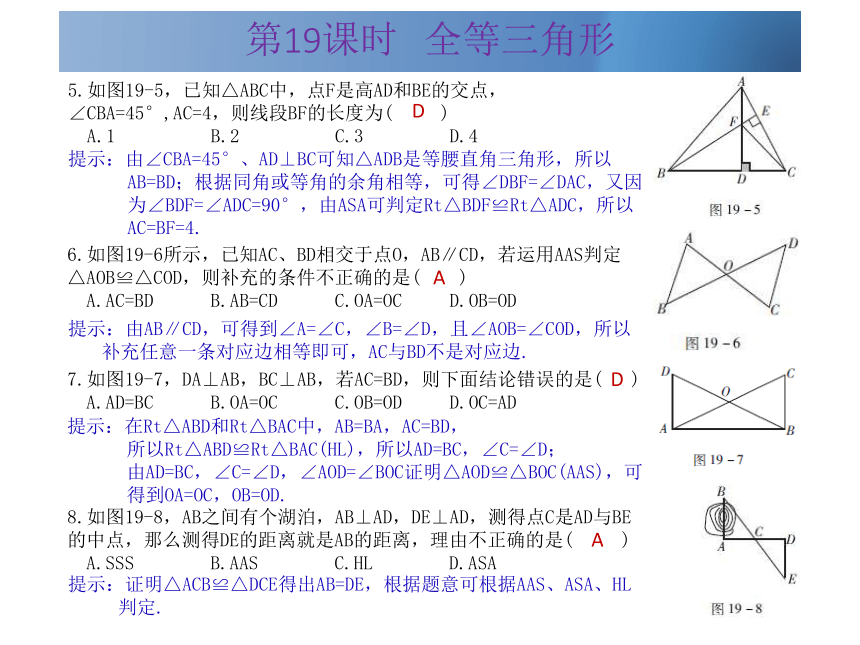
A.∠B=∠E B.BC= ED C.AF=DC D.AB=EF提示:根据基本事实SAS,由已知条件可知证明△ABC和△DEF全等,缺少一条对应边相等,由AF=DC,可得AF+CF=DC+CF,即AC=DF,故选择C符合题意.CD第19课时 全等三角形 5.如图19-5,已知△ABC中,点F是高AD和BE的交点,∠CBA=45°,AC=4,则线段BF的长度为( )
A.1 B.2 C.3 D.4提示:由∠CBA=45°、AD⊥BC可知△ADB是等腰直角三角形,所以AB=BD;根据同角或等角的余角相等,可得∠DBF=∠DAC,又因为∠BDF=∠ADC=90°,由ASA可判定Rt△BDF≌Rt△ADC,所以AC=BF=4.6.如图19-6所示,已知AC、BD相交于点O,AB∥CD,若运用AAS判定△AOB≌△COD,则补充的条件不正确的是( )
A.AC=BD B.AB=CD C.OA=OC D.OB=OD提示:由AB∥CD,可得到∠A=∠C,∠B=∠D,且∠AOB=∠COD,所以补充任意一条对应边相等即可,AC与BD不是对应边.7.如图19-7,DA⊥AB,BC⊥AB,若AC=BD,则下面结论错误的是( )
A.AD=BC B.OA=OC C.OB=OD D.OC=AD提示:在Rt△ABD和Rt△BAC中,AB=BA,AC=BD,
所以Rt△ABD≌Rt△BAC(HL),所以AD=BC,∠C=∠D;
由AD=BC,∠C=∠D,∠AOD=∠BOC证明△AOD≌△BOC(AAS),可得到OA=OC,OB=OD.DDA8.如图19-8,AB之间有个湖泊,AB⊥AD,DE⊥AD,测得点C是AD与BE的中点,那么测得DE的距离就是AB的距离,理由不正确的是( )
A.SSS B.AAS C.HL D.ASA提示:证明△ACB≌△DCE得出AB=DE,根据题意可根据AAS、ASA、HL判定.A第19课时 全等三角形考点分类三 角平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.
角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.9.如图19-9,角平分线的性质:角平分线上的点到这个角的两边距离相等,其理论依据是全等三角形判定定理( )
A.SAS B.HL C.AAS D.ASA10.如图19-10所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系下列说法正确的是( )
A.一定相等 B.一定不相等
C.当BD=CD时相等 D.当DE=DF时相等提示:如图,∵OP是∠AOB的平分线,∴∠AOP=∠BOP,
∵PA⊥OA于A,PB⊥OB于B,
∴∠PAO=∠PBO=90°,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(AAS).提示:根据到角的两边距离相等的点在角的平分线上,故选D.CD?第19课时 全等三角形真题演练?层层推进
基础题1.(2013?呼伦贝尔)如图19-11,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°提示:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
即∠ACA′+∠A′CB=∠B′CB+∠A′CB,
∴∠ACA′=∠B′CB,
又∠B′CB=30°
∴∠ACA′=30°.提示:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;2.(2014?黔西南州)如图19-12,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°BC第19课时 全等三角形 3.(2014?南昌)如图19-13,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC提示:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,
,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,
,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,
,∴△ABC≌△DEF,故D选项错误.提示:作DE⊥AB于E.∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.∴△ABD的面积为 ×3×10=15.4. (2014?长春)如图19-14,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 .C???15?第19课时 全等三角形 5.如图19-15,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是 .提示:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC =S△ABD +S△ACD ,
∴ ×4×2+ ×AC×2=7,
解得AC=3.解:AC=DF.
证明:∵BF=EC,∴BF-CF=EC-CF,∴BC=EF,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(SAS).6.(2014?漳州)(SAS)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)3??提高题?第19课时 全等三角形 7.(2014?邵阳)如图19-16,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.解:(1)△ABE≌△CDF,△AFD≌△CEB;
(2)∵AB∥CD,∴∠1=∠2,
∵AF=CE,∴AF+EF=CE+EF,即AE=FC,
在△ABE和△CDF中, ,
∴△ABE≌△CDF(AAS).证明:连接AD,
在△ACD和△ABD中, ,
∴△ACD≌△ABD(SSS),∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,∴DE=DF.8.(2014?黄冈)已知,如图19-17,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.?拔高题?第19课时 全等三角形课时作业一、选择题1.如图19-1,△ABC≌△A’B’C’,∠BAB’=30°,则∠CAC’的度数为( )
A.20° B.30° C.35° D.40°2.如图19-2,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
A. BD=CD B. ∠BAC=90° C. BD=AC D.∠B=45°3.如图19-3,AE平分∠BAC,运用ASA证明△ABD≌△ACD需要补充的条件是( ).
A.∠BDE=∠CDE B.AB=AC C.BD=CD D.∠BAE=∠C提示:根据全等三角形的性质,可得∠BAC=∠B’AC’, ∠BAC-∠BAC=∠B’AC’-∠BAC,即∠BAB’=∠CAC’=30°4.如图19-4所示,已知AB=DC,若用定理SSS证明△ABC≌△DCB,则需要添加的条件是( )
A.OA=OD B.OB=OC C.BC=CB D.AC=DBAABD提示:由BD=CD,∠ADB=∠ADC=90°,AD=AD,根据SAS即可判定△ABD≌△ACD,故选择A符合题意.提示:已知∠BAD=∠CAD,AD=AD,根据ASA可知证明△ABD≌△ACD需要补充∠ADB=∠ADC,由选项A即可推理出∠ADB=∠ADC.提示:在△ABC和△DCB中,已知AB=DC,BC=CB,第三条对应边为AC和DB,根据SSS判定△ABC≌△DCB,故添加条件AC=DB.第19课时 全等三角形课时作业 5.如图19-5所示,点A、D、C和F在一条直线上,AB∥DE,BC∥EF,且AB=DE,则下列结论不正确的是( )
A.∠E=∠F B.∠B=∠E C.AD=CF D.BC=EF提示:由AB∥DE、BC∥EF,可得∠A= ∠EDF,∠F=∠ACB,又因为AB=DE,所以△ABC≌△DEF(AAS),根据全等三角形的性质,选项B、C、D都正确.A二、填空题6.如图19-6,∠C=∠D=90°,若运用HL判定Rt△ABD≌Rt△BAC,则需要补充的条件是 .提示:根据题意,两个直角三角形的斜边是公共边,补充一条直角边对应相等.8.如图19-8,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,根据SAS可补充的条件是 ;根据ASA可补充的条件是 .7.如图19-7,已知∠C=∠D, OC=OD,AC与BD相交于点O,则图中相等的线段共有 组.(除同一线段)提示:判定定理SAS,即三角形的两边与两边的夹角对应相等,则两个三角形全等;判定定理ASA,即三角形的两角与两角的夹边对应相等,则两个三角形全等.根据判定定理的条件补充条件即可.提示:根据ASA判定△AOD≌△BOC,可得OC=OD,AD=BC,OA=OB,BD=AC.AD=BC(或AC=BD)4∠B=∠DAC=AE第19课时 全等三角形课时作业 9.如图19-9,D、E是BC边上的两点,且AB=AC,AD=AE,要使△ABE≌△ACD,报据SSS的判断方法,还需要给出的条件是 或 .提示:∵BD=CE,∴BD+DE=CE+DE,∴BE=CD,
在△ABE和△ACD中, ,
∴△ABE≌△ACD(SSS),
故答案为:BE=CD,BD=CE.10.如图19-10,△ABC中,∠C=90°,以B点为圆心,小于BC长为半径画弧,分别交边BA、BC于M、N两点;再分别以M、N为圆心,大于 MN长为半径画弧,两弧交于点P,射线BP交AC于点(D)若CD=5cm,则点D到AB的距离为 cm.提示:连接PN,PM,过点D作DE⊥AB于E,
在△BPN和△BPM中,
∵ ,
∴△BPN≌△BPM(SSS),∴∠PBN=∠PBM,
∵△ABC中,∠C=90°,即CD⊥BC,
∴DE=CD=5cm.
∴点D到AB的距离为5cm.
5BD=CEBE=CD???第19课时 全等三角形课时作业三、解答题11.如图19-11, A、B、C、D在同一直线上,AD=BC,AE=BF,CE=DF.
请你证明:DF∥CE.证明:∵AD=BC,∴AD+CD=BC+CD,即AC=BD,
又∵AE=BF,CE=DF,∴△BDF≌△ACE(SSS),
∴∠1=∠2,∴DF∥CE.12.如图19-12,已知Rt△ABC≌Rt△ADE,BC与DE相交于点F,连接CD、EB.
求证:△ADC≌△ABE.证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,∠CAB=∠EAD,AB=AD(即AD=AB),
∴∠CAD=∠EAB, ∴△ACD≌△AEB(SAS).13.如图19-13,已知AC平分∠BAD,CF⊥AD于F,CE⊥AB于E,DC=BC.
求证:△CFD≌△CEB.解:∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF(角平分线上的点到角的两边的距离相等);
在Rt△BCE和Rt△DCF中,
∵ , ∴Rt△BCE≌Rt△DCF(HL).?第19课时 全等三角形课时作业 14.如图19-14,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.证明:(1)如图,连接AP并延长,
∵PE⊥AB,PF⊥AC
∴∠AEP=∠AFP=90°
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
,
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.?结束谢谢!
考点分类一 全等三角形的概念与性质 全等三角形:能够完全重合的两个三角形叫做全等三角形.
全等三角形的性质:(1)全等三角形的对应角、对应边分别相等;
(2)全等三角形中的对应线段(角平分线、中线、高)相等、周长相等、面积相等.1.如图19-1所示,已知△ABC≌△BAD,如果AB=5cm,BC=7cm,AC=10cm,那么BD等于( )
A.10cm B.7 cm C.5 cm D.无法确定提示:根据全等三角形的性质,对应边相等,AC=BD=10cm.2.如图19-2,如果△ABC≌△DCB,AB=10,AC=12,BC=8,则△DCB的周长是( )
A.20 B.30 C.40 D.45提示:根据全等三角形的性质,对应边相等,所以AB=CD=10,AC=BD=12,BC=CB=8,
所以△DCB的周长=CD+BD+CB=10+12+8=30.BA第19课时 全等三角形考点分类二 全等三角形的判定(1)如果两个三角形的三条边分别相等,那么这两个三角形全等,简记为SSS;
(2)如果两个三角形有两边及其夹角分别对应相等,那么这两个三角形全等,简记为SAS;
(3)如果两个三角形的两角及其夹边分别对应相等,那么这两个三角形全等,简记为ASA;
(4)如果三角形的两角及其中一角的对边分别对应相等,那么这两个三角形全等,简记为AAS.
(5)如果两个直角三角形的斜边及一条直角边分别对应相等,那么这两个直角三角形全等,简记为HL.3.如图19-3所示,已知AB=DC,若用定理SSS证明△ABC≌△DCB,则需要添加的条件是( )
A.OA=OD B.OB=OC C.BC=CB D.AC=DB提示:在△ABC和△DCB中,已知AB=DC,BC=CB,第三条对应边为AC和DB,根据SSS判定△ABC≌△DCB,故添加条件AC=DB.4.如图19-4,已知∠A=∠D, ∠BCA=∠EFD,要得到△ABC≌△DEF,还应给出的条件是( )
A.∠B=∠E B.BC= ED C.AF=DC D.AB=EF提示:根据基本事实SAS,由已知条件可知证明△ABC和△DEF全等,缺少一条对应边相等,由AF=DC,可得AF+CF=DC+CF,即AC=DF,故选择C符合题意.CD第19课时 全等三角形 5.如图19-5,已知△ABC中,点F是高AD和BE的交点,∠CBA=45°,AC=4,则线段BF的长度为( )
A.1 B.2 C.3 D.4提示:由∠CBA=45°、AD⊥BC可知△ADB是等腰直角三角形,所以AB=BD;根据同角或等角的余角相等,可得∠DBF=∠DAC,又因为∠BDF=∠ADC=90°,由ASA可判定Rt△BDF≌Rt△ADC,所以AC=BF=4.6.如图19-6所示,已知AC、BD相交于点O,AB∥CD,若运用AAS判定△AOB≌△COD,则补充的条件不正确的是( )
A.AC=BD B.AB=CD C.OA=OC D.OB=OD提示:由AB∥CD,可得到∠A=∠C,∠B=∠D,且∠AOB=∠COD,所以补充任意一条对应边相等即可,AC与BD不是对应边.7.如图19-7,DA⊥AB,BC⊥AB,若AC=BD,则下面结论错误的是( )
A.AD=BC B.OA=OC C.OB=OD D.OC=AD提示:在Rt△ABD和Rt△BAC中,AB=BA,AC=BD,
所以Rt△ABD≌Rt△BAC(HL),所以AD=BC,∠C=∠D;
由AD=BC,∠C=∠D,∠AOD=∠BOC证明△AOD≌△BOC(AAS),可得到OA=OC,OB=OD.DDA8.如图19-8,AB之间有个湖泊,AB⊥AD,DE⊥AD,测得点C是AD与BE的中点,那么测得DE的距离就是AB的距离,理由不正确的是( )
A.SSS B.AAS C.HL D.ASA提示:证明△ACB≌△DCE得出AB=DE,根据题意可根据AAS、ASA、HL判定.A第19课时 全等三角形考点分类三 角平分线的性质角平分线的性质:角的平分线上的点到角的两边的距离相等.
角平分线的判定:角的内部到角的两边的距离相等的点在角的平分线上.9.如图19-9,角平分线的性质:角平分线上的点到这个角的两边距离相等,其理论依据是全等三角形判定定理( )
A.SAS B.HL C.AAS D.ASA10.如图19-10所示,若DE⊥AB,DF⊥AC,则对于∠1和∠2的大小关系下列说法正确的是( )
A.一定相等 B.一定不相等
C.当BD=CD时相等 D.当DE=DF时相等提示:如图,∵OP是∠AOB的平分线,∴∠AOP=∠BOP,
∵PA⊥OA于A,PB⊥OB于B,
∴∠PAO=∠PBO=90°,
在△AOP和△BOP中,
,
∴△AOP≌△BOP(AAS).提示:根据到角的两边距离相等的点在角的平分线上,故选D.CD?第19课时 全等三角形真题演练?层层推进
基础题1.(2013?呼伦贝尔)如图19-11,△ACB≌△A′CB′,∠BCB′=30°,则∠ACA′的度数为( )
A.20° B.30° C.35° D.40°提示:∵△ACB≌△A′CB′,
∴∠ACB=∠A′CB′,
即∠ACA′+∠A′CB=∠B′CB+∠A′CB,
∴∠ACA′=∠B′CB,
又∠B′CB=30°
∴∠ACA′=30°.提示:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故C选项符合题意;
D、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故D选项不符合题意;2.(2014?黔西南州)如图19-12,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC
C.∠BCA=∠DCA D.∠B=∠D=90°BC第19课时 全等三角形 3.(2014?南昌)如图19-13,AB∥DE,AC∥DF,AC=DF,下列条件中不能判断△ABC≌△DEF的是( )
A.AB=DE B.∠B=∠E C.EF=BC D.EF∥BC提示:∵AB∥DE,AC∥DF,∴∠A=∠D,
(1)AB=DE,则△ABC和△DEF中,
,∴△ABC≌△DEF,故A选项错误;
(2)∠B=∠E,则△ABC和△DEF中,
,∴△ABC≌△DEF,故B选项错误;
(3)EF=BC,无法证明△ABC≌△DEF(ASS);故C选项正确;
(4)∵EF∥BC,AB∥DE,∴∠B=∠E,则△ABC和△DEF中,
,∴△ABC≌△DEF,故D选项错误.提示:作DE⊥AB于E.∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=CD=3.∴△ABD的面积为 ×3×10=15.4. (2014?长春)如图19-14,在△ABC中,∠C=90°,AB=10,AD是△ABC的一条角平分线.若CD=3,则△ABD的面积为 .C???15?第19课时 全等三角形 5.如图19-15,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是 .提示:如图,过点D作DF⊥AC于F,
∵AD是△ABC中∠BAC的角平分线,DE⊥AB,
∴DE=DF,
由图可知,S△ABC =S△ABD +S△ACD ,
∴ ×4×2+ ×AC×2=7,
解得AC=3.解:AC=DF.
证明:∵BF=EC,∴BF-CF=EC-CF,∴BC=EF,
在△ABC和△DEF中, ,
∴△ABC≌△DEF(SAS).6.(2014?漳州)(SAS)如图,点C,F在线段BE上,BF=EC,∠1=∠2,请你添加一个条件,使△ABC≌△DEF,并加以证明.(不再添加辅助线和字母)3??提高题?第19课时 全等三角形 7.(2014?邵阳)如图19-16,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.解:(1)△ABE≌△CDF,△AFD≌△CEB;
(2)∵AB∥CD,∴∠1=∠2,
∵AF=CE,∴AF+EF=CE+EF,即AE=FC,
在△ABE和△CDF中, ,
∴△ABE≌△CDF(AAS).证明:连接AD,
在△ACD和△ABD中, ,
∴△ACD≌△ABD(SSS),∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,∴DE=DF.8.(2014?黄冈)已知,如图19-17,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.?拔高题?第19课时 全等三角形课时作业一、选择题1.如图19-1,△ABC≌△A’B’C’,∠BAB’=30°,则∠CAC’的度数为( )
A.20° B.30° C.35° D.40°2.如图19-2,已知AD是△ABC的边BC上的高,下列能使△ABD≌△ACD的条件是( )
A. BD=CD B. ∠BAC=90° C. BD=AC D.∠B=45°3.如图19-3,AE平分∠BAC,运用ASA证明△ABD≌△ACD需要补充的条件是( ).
A.∠BDE=∠CDE B.AB=AC C.BD=CD D.∠BAE=∠C提示:根据全等三角形的性质,可得∠BAC=∠B’AC’, ∠BAC-∠BAC=∠B’AC’-∠BAC,即∠BAB’=∠CAC’=30°4.如图19-4所示,已知AB=DC,若用定理SSS证明△ABC≌△DCB,则需要添加的条件是( )
A.OA=OD B.OB=OC C.BC=CB D.AC=DBAABD提示:由BD=CD,∠ADB=∠ADC=90°,AD=AD,根据SAS即可判定△ABD≌△ACD,故选择A符合题意.提示:已知∠BAD=∠CAD,AD=AD,根据ASA可知证明△ABD≌△ACD需要补充∠ADB=∠ADC,由选项A即可推理出∠ADB=∠ADC.提示:在△ABC和△DCB中,已知AB=DC,BC=CB,第三条对应边为AC和DB,根据SSS判定△ABC≌△DCB,故添加条件AC=DB.第19课时 全等三角形课时作业 5.如图19-5所示,点A、D、C和F在一条直线上,AB∥DE,BC∥EF,且AB=DE,则下列结论不正确的是( )
A.∠E=∠F B.∠B=∠E C.AD=CF D.BC=EF提示:由AB∥DE、BC∥EF,可得∠A= ∠EDF,∠F=∠ACB,又因为AB=DE,所以△ABC≌△DEF(AAS),根据全等三角形的性质,选项B、C、D都正确.A二、填空题6.如图19-6,∠C=∠D=90°,若运用HL判定Rt△ABD≌Rt△BAC,则需要补充的条件是 .提示:根据题意,两个直角三角形的斜边是公共边,补充一条直角边对应相等.8.如图19-8,已知AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,根据SAS可补充的条件是 ;根据ASA可补充的条件是 .7.如图19-7,已知∠C=∠D, OC=OD,AC与BD相交于点O,则图中相等的线段共有 组.(除同一线段)提示:判定定理SAS,即三角形的两边与两边的夹角对应相等,则两个三角形全等;判定定理ASA,即三角形的两角与两角的夹边对应相等,则两个三角形全等.根据判定定理的条件补充条件即可.提示:根据ASA判定△AOD≌△BOC,可得OC=OD,AD=BC,OA=OB,BD=AC.AD=BC(或AC=BD)4∠B=∠DAC=AE第19课时 全等三角形课时作业 9.如图19-9,D、E是BC边上的两点,且AB=AC,AD=AE,要使△ABE≌△ACD,报据SSS的判断方法,还需要给出的条件是 或 .提示:∵BD=CE,∴BD+DE=CE+DE,∴BE=CD,
在△ABE和△ACD中, ,
∴△ABE≌△ACD(SSS),
故答案为:BE=CD,BD=CE.10.如图19-10,△ABC中,∠C=90°,以B点为圆心,小于BC长为半径画弧,分别交边BA、BC于M、N两点;再分别以M、N为圆心,大于 MN长为半径画弧,两弧交于点P,射线BP交AC于点(D)若CD=5cm,则点D到AB的距离为 cm.提示:连接PN,PM,过点D作DE⊥AB于E,
在△BPN和△BPM中,
∵ ,
∴△BPN≌△BPM(SSS),∴∠PBN=∠PBM,
∵△ABC中,∠C=90°,即CD⊥BC,
∴DE=CD=5cm.
∴点D到AB的距离为5cm.
5BD=CEBE=CD???第19课时 全等三角形课时作业三、解答题11.如图19-11, A、B、C、D在同一直线上,AD=BC,AE=BF,CE=DF.
请你证明:DF∥CE.证明:∵AD=BC,∴AD+CD=BC+CD,即AC=BD,
又∵AE=BF,CE=DF,∴△BDF≌△ACE(SSS),
∴∠1=∠2,∴DF∥CE.12.如图19-12,已知Rt△ABC≌Rt△ADE,BC与DE相交于点F,连接CD、EB.
求证:△ADC≌△ABE.证明:∵Rt△ABC≌Rt△ADE,
∴AC=AE,∠CAB=∠EAD,AB=AD(即AD=AB),
∴∠CAD=∠EAB, ∴△ACD≌△AEB(SAS).13.如图19-13,已知AC平分∠BAD,CF⊥AD于F,CE⊥AB于E,DC=BC.
求证:△CFD≌△CEB.解:∵AC平分∠BAD,CE⊥AB,CF⊥AD,
∴CE=CF(角平分线上的点到角的两边的距离相等);
在Rt△BCE和Rt△DCF中,
∵ , ∴Rt△BCE≌Rt△DCF(HL).?第19课时 全等三角形课时作业 14.如图19-14,P是∠BAC内的一点,PE⊥AB,PF⊥AC,垂足分别为点E,F,AE=AF.
求证:
(1)PE=PF;
(2)点P在∠BAC的角平分线上.证明:(1)如图,连接AP并延长,
∵PE⊥AB,PF⊥AC
∴∠AEP=∠AFP=90°
又AE=AF,AP=AP,
∵在Rt△AFP和Rt△AEP中
,
∴Rt△AEP≌Rt△AFP(HL),
∴PE=PF.
(2)∵Rt△AEP≌Rt△AFP,
∴∠EAP=∠FAP,
∴AP是∠BAC的角平分线,
故点P在∠BAC的角平分线上.?结束谢谢!
同课章节目录
