物理人教版(2019)选择性必修第一册1.3动量守恒定律(共20张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册1.3动量守恒定律(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 996.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-10-27 21:14:55 | ||
图片预览






文档简介
(共20张PPT)
第一章 动量守恒定律
3、动量守恒定律
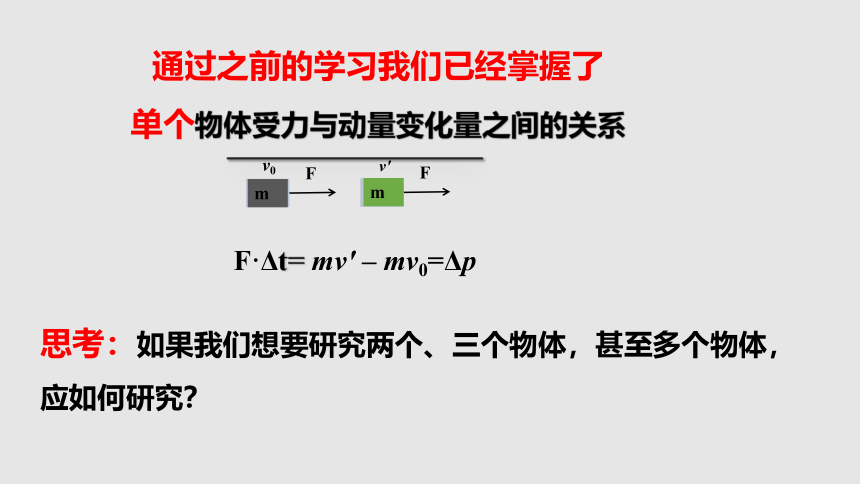
F·Δt= mv' – mv0=Δp
思考:如果我们想要研究两个、三个物体,甚至多个物体,应如何研究?
F
v0
v'
F
m
m
通过之前的学习我们已经掌握了
单个物体受力与动量变化量之间的关系
一、系统、内力和外力
注意:内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
1、系统:我们把两个(或多个)相互作用的物体构成的整体叫做一个力学系统。系统可按解决问题的需要灵活选取。
2、内力:系统中物体间的相互作用力叫做内力。
3、外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
选ABC为系统:A与C、B与C之间的摩擦力为内力还是外力?
选AB为系统:A与C、B与C之间的摩擦力为内力还是外力?
设置物理情景:在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
B
v2
m2
A
v1
m1
思考:下面我们用动量定理来分别研究A和B的动量变化!
二、相互作用的两个物体的动量改变
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
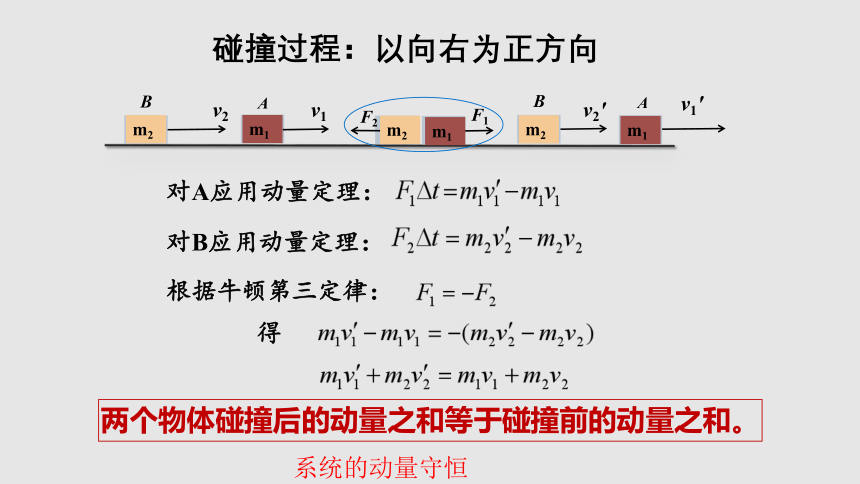
碰撞过程:以向右为正方向
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之和等于碰撞前的动量之和。
F1
F2
m2
m1
系统的动量守恒
碰撞过程
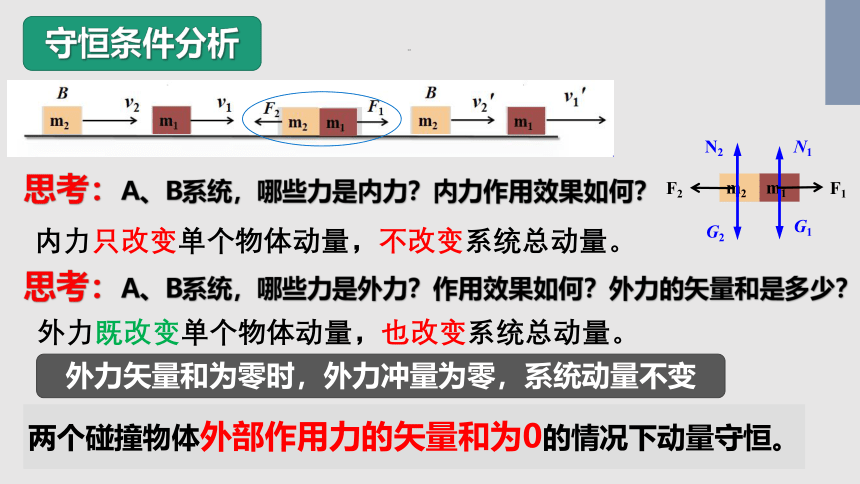
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
思考:A、B系统,哪些力是内力?内力作用效果如何?
外力矢量和为零时,外力冲量为零,系统动量不变
守恒条件分析
思考:A、B系统,哪些力是外力?作用效果如何?外力的矢量和是多少?
内力只改变单个物体动量,不改变系统总动量。
外力既改变单个物体动量,也改变系统总动量。
m2
m1
G1
N1
N2
G2
F2
F1
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统作用前的总动量等于作用后的总动量).
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(系统总动量的变化量为零)
三、动量守恒定律
(1)矢量性:动量守恒定律是矢量式,对于作用前后的运动方向都在同一直线上的问题,应选取统一的正方向。
(2)瞬时性:动量是一个状态量,是作用前(或某一时刻)系统的动量和等于作用后(或另一时刻)系统的动量和。
(3)相对性:速度相对于同一参考系,一般以地球为参考系。
(4)系统性:描述的对象是由两个以上的物体构成的系统 。
3.理 解
①动量守恒定律不仅适用于正碰,也适用于斜碰;不仅适用于碰撞(时间较短),也适用于任何形式的相互作用(时间可以较长);不仅适用于两个物体组成的系统,也适用于两个以上物体组成的系统。
4、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
5、守恒条件的理解:
(1)理想条件:系统不受外力或F合外=0
(2)近似条件:系统所受外力之和不为零,但系统的内力远大于外力,外力可以忽略不计,如:碰撞、爆炸瞬间
(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒,
系统不受外力或F合外=0
光滑水平面
粗糙水平面
光滑水平面
内力
1、子弹-木块
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行。
①进入瞬间:系统动量守恒吗?机械能守恒吗?
②一起滑行:系统动量守恒吗?
若桌面粗糙,结果如何
合外力为零,守恒;
摩擦生热,机械能不守恒
合外力为零,动量守恒
内力远大于外力,动量守恒,
外力不能忽略,动量减少不守恒
①进入时:系统动量守恒吗?
②一起滑行时:系统动量怎么样?
所以,从进入到一起滑行全程系统动量守恒,求末速度时直接动量守恒
所以,求滑行一段的末速度时,先动量守恒后动能定理
四、动量守恒的判断
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
2、子弹-木块-弹簧
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面光滑、共速后压缩弹簧过程、子弹和木块组成的系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
斜面置于光滑水平面上,木块沿光滑斜面滑下,则木块与斜面组成的系统受到几个作用力?哪些力是内力?哪些是外力?系统动量守恒吗?
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
3、斜面-滑块
思考:在物块下滑的过程中系统水平方向动量守恒吗?
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
4、铁锤-小车
A. 左右来回运动 B. 向左运动
C. 向右运动 D. 静止不动
A
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
m1v1+m2v2=m1v1′+m2v2′
五、动量守恒的计算
1.一枚在空中飞行的火箭质量为m,在某时刻的速度大小为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度大小为v1。求炸裂后另一块的速度v2。
典例分析
解:球和车组成的系统水平方向动量守恒,取水平向左为正方向,设球、车分离时,球的速度大小为v1,方向向左,车的速度大小为v2,方向向右,由动量守恒定律得
0=mv1-Mv2
由机械能守恒定律得
联立两式解得
3. 两只小船质量分别为m1=500 kg、m2=1000 kg,它们平行逆向航行,航线邻近,当它们头尾相齐时,从每一只船上各投质量m=50 kg的麻袋到对面的船上,如图所示,结果质量较小的船停了下来,另一只船则以v=8.5 m/s的速度沿原方向航行,若水的阻力不计,求在交换麻袋前两只船的速率。
解:以质量较小的船的速度方向为正方向,选取质量较小的船和从质量较大的船投过去的麻袋组成的系统为研究对象,根据动量守恒定律有
(m1-m)v1-mv2=0
选取两船和两个麻袋组成的系统为研究对象有
选取质量较大的船和从质量较小的船投过去的麻袋组成的系统为研究对象,根据动量守恒定律有
mv1-(m2-m)v2=-m2v
m1v1-m2v2=-m2v
联立任意两式解得v1=1 m/s,v2=9 m/s。
4. 如图所示,质量为2 kg的平板车B上表面水平,原来静止在光滑水平面上,平板车一端静止着一块质量为2 kg的物体A,一颗质量为m=0.01 kg的子弹以速度v0=600 m/s水平瞬间射穿A后,速度变为v′=100 m/s,已知A、B之间的动摩擦因数为0.05,平板车B足够长,求:(1)子弹穿过A瞬间,A的速度大小;(2)B最终的速度大小。
解 (1)子弹与A作用过程时间极短,内力远大于外力,故子弹与A组成的系统动量守恒,取v0方向为正方向,由动量守恒定律得
mv0=mv′+mAvA 解得vA=2.5 m/s。
(2)子弹射穿A后,物体A与平板车B组成的系统动量守恒,最终A、B共速,由动量守恒定律得
mAvA=(mA+mB)vB 解得vB=1.25 m/s。
谢谢观看!
第一章 动量守恒定律
3、动量守恒定律
F·Δt= mv' – mv0=Δp
思考:如果我们想要研究两个、三个物体,甚至多个物体,应如何研究?
F
v0
v'
F
m
m
通过之前的学习我们已经掌握了
单个物体受力与动量变化量之间的关系
一、系统、内力和外力
注意:内力和外力的区分依赖于系统的选取,只有在确定了系统后,才能确定内力和外力。
1、系统:我们把两个(或多个)相互作用的物体构成的整体叫做一个力学系统。系统可按解决问题的需要灵活选取。
2、内力:系统中物体间的相互作用力叫做内力。
3、外力:系统以外的物体施加给系统内任何一个物体的力,叫做外力。
选ABC为系统:A与C、B与C之间的摩擦力为内力还是外力?
选AB为系统:A与C、B与C之间的摩擦力为内力还是外力?
设置物理情景:在光滑水平面上做匀速运动的两个物体A、B,质量分别为m1和m2,沿着同一直线向相同的方向运动,速度分别是v1、v2,且v2>v1。当B追上了A时发生碰撞。碰撞后A、B的速度分别为v1′和v2′。
B
v2
m2
A
v1
m1
思考:下面我们用动量定理来分别研究A和B的动量变化!
二、相互作用的两个物体的动量改变
B
v2
m2
A
v1
m1
B
v2'
m2
A
v1'
m1
碰撞过程:以向右为正方向
对A应用动量定理:
对B应用动量定理:
根据牛顿第三定律:
得
两个物体碰撞后的动量之和等于碰撞前的动量之和。
F1
F2
m2
m1
系统的动量守恒
碰撞过程
两个碰撞物体外部作用力的矢量和为0的情况下动量守恒。
思考:A、B系统,哪些力是内力?内力作用效果如何?
外力矢量和为零时,外力冲量为零,系统动量不变
守恒条件分析
思考:A、B系统,哪些力是外力?作用效果如何?外力的矢量和是多少?
内力只改变单个物体动量,不改变系统总动量。
外力既改变单个物体动量,也改变系统总动量。
m2
m1
G1
N1
N2
G2
F2
F1
如果一个系统不受外力,或者所受外力的矢量和为0,
这个系统的总动量保持不变。这就是动量守恒定律。
1.内容:
2.表达式:
(3)Δp=0
(1)p=p′或m1v1+m2v2=m1v1′+m2v2′
(2)Δp1=-Δp2 或 m1Δv1=-m2Δv2
(系统作用前的总动量等于作用后的总动量).
(系统内一个物体的动量变化与另一物体的动量变化等大反向)
(系统总动量的变化量为零)
三、动量守恒定律
(1)矢量性:动量守恒定律是矢量式,对于作用前后的运动方向都在同一直线上的问题,应选取统一的正方向。
(2)瞬时性:动量是一个状态量,是作用前(或某一时刻)系统的动量和等于作用后(或另一时刻)系统的动量和。
(3)相对性:速度相对于同一参考系,一般以地球为参考系。
(4)系统性:描述的对象是由两个以上的物体构成的系统 。
3.理 解
①动量守恒定律不仅适用于正碰,也适用于斜碰;不仅适用于碰撞(时间较短),也适用于任何形式的相互作用(时间可以较长);不仅适用于两个物体组成的系统,也适用于两个以上物体组成的系统。
4、适用范围:
②定律既适用于宏观物体的相互作用,也适用于微观粒子的相互作用,不管是低速还是高速问题均适用。
5、守恒条件的理解:
(1)理想条件:系统不受外力或F合外=0
(2)近似条件:系统所受外力之和不为零,但系统的内力远大于外力,外力可以忽略不计,如:碰撞、爆炸瞬间
(3)方向条件:系统受外力,且不能忽略,但在某一方向上所受外力为0, 则系统在该方向上动量守恒,
系统不受外力或F合外=0
光滑水平面
粗糙水平面
光滑水平面
内力
1、子弹-木块
子弹沿水平方向射入光滑水平桌面上的木块后,一起滑行。
①进入瞬间:系统动量守恒吗?机械能守恒吗?
②一起滑行:系统动量守恒吗?
若桌面粗糙,结果如何
合外力为零,守恒;
摩擦生热,机械能不守恒
合外力为零,动量守恒
内力远大于外力,动量守恒,
外力不能忽略,动量减少不守恒
①进入时:系统动量守恒吗?
②一起滑行时:系统动量怎么样?
所以,从进入到一起滑行全程系统动量守恒,求末速度时直接动量守恒
所以,求滑行一段的末速度时,先动量守恒后动能定理
四、动量守恒的判断
子弹A沿水平方向射入水平桌面上的木块B后,一起压缩弹簧压缩到最短。
2、子弹-木块-弹簧
①桌面光滑、进入过程、子弹和木块系统动量怎样?
②桌面光滑、共速后压缩弹簧过程、子弹和木块组成的系统动量怎样?
外力(弹簧弹力)不能忽略,动量不守恒,但子弹、木块、弹簧系统机械能守恒
A
B
子弹射入木块的过程,时间极短暂,可认为弹簧仍保持原长,
此瞬间子弹与木块的摩擦为内力,系统合外力为零,
系统动量守恒,
思想方法:理想模型法,抓住重要因素忽略次要因素
斜面置于光滑水平面上,木块沿光滑斜面滑下,则木块与斜面组成的系统受到几个作用力?哪些力是内力?哪些是外力?系统动量守恒吗?
竖直方向失重:N<(M+m)g 系统动量不守恒。
N
Mg
mg
N1
N’1
思考:斜面粗糙但地面仍然光滑,系统水平方向动量还守恒吗?
系统水平方向不受外力作用,水平方向动量守恒
3、斜面-滑块
思考:在物块下滑的过程中系统水平方向动量守恒吗?
滑块和斜面间的摩擦为内力,系统水平方向动量守恒
在光滑的水平面上有一辆平板车,一个人站在车上用大锤敲打车的左端,如图所示,在连续地敲打下,这辆车
人、车系统水平方向不受外力作用,水平方向动量守恒 ,系统初动量为零, 任何一时刻系统动量矢量和必定都为零,当锤向左运动,小车就向右运动,大锤向右运动,小车向左运动,铁锤静止,小车也静止, 所以在水平面上左、右往返运动.车不会持续地向右驶去.
4、铁锤-小车
A. 左右来回运动 B. 向左运动
C. 向右运动 D. 静止不动
A
⑴找:找研究对象(系统包括那几个物体)和研究过程;
⑵析:进行受力分析,判断系统动量是否守恒(或在某一方向是否守恒);
⑶定:规定正方向,确定初末状态动量正负号;
⑷列:由动量守恒定律列方程;
⑸解:解方程,得出最后的结果,并对结果进行分析。
应用动量守恒定律解题的基本步骤和方法
m1v1+m2v2=m1v1′+m2v2′
五、动量守恒的计算
1.一枚在空中飞行的火箭质量为m,在某时刻的速度大小为v,方向水平,燃料即将耗尽。此时,火箭突然炸裂成两块,其中质量为m1的一块沿着与v相反的方向飞去,速度大小为v1。求炸裂后另一块的速度v2。
典例分析
解:球和车组成的系统水平方向动量守恒,取水平向左为正方向,设球、车分离时,球的速度大小为v1,方向向左,车的速度大小为v2,方向向右,由动量守恒定律得
0=mv1-Mv2
由机械能守恒定律得
联立两式解得
3. 两只小船质量分别为m1=500 kg、m2=1000 kg,它们平行逆向航行,航线邻近,当它们头尾相齐时,从每一只船上各投质量m=50 kg的麻袋到对面的船上,如图所示,结果质量较小的船停了下来,另一只船则以v=8.5 m/s的速度沿原方向航行,若水的阻力不计,求在交换麻袋前两只船的速率。
解:以质量较小的船的速度方向为正方向,选取质量较小的船和从质量较大的船投过去的麻袋组成的系统为研究对象,根据动量守恒定律有
(m1-m)v1-mv2=0
选取两船和两个麻袋组成的系统为研究对象有
选取质量较大的船和从质量较小的船投过去的麻袋组成的系统为研究对象,根据动量守恒定律有
mv1-(m2-m)v2=-m2v
m1v1-m2v2=-m2v
联立任意两式解得v1=1 m/s,v2=9 m/s。
4. 如图所示,质量为2 kg的平板车B上表面水平,原来静止在光滑水平面上,平板车一端静止着一块质量为2 kg的物体A,一颗质量为m=0.01 kg的子弹以速度v0=600 m/s水平瞬间射穿A后,速度变为v′=100 m/s,已知A、B之间的动摩擦因数为0.05,平板车B足够长,求:(1)子弹穿过A瞬间,A的速度大小;(2)B最终的速度大小。
解 (1)子弹与A作用过程时间极短,内力远大于外力,故子弹与A组成的系统动量守恒,取v0方向为正方向,由动量守恒定律得
mv0=mv′+mAvA 解得vA=2.5 m/s。
(2)子弹射穿A后,物体A与平板车B组成的系统动量守恒,最终A、B共速,由动量守恒定律得
mAvA=(mA+mB)vB 解得vB=1.25 m/s。
谢谢观看!
