湖北省宜昌市宜都市重点中学2023-2024学年高二上学期期中考试数学试题(含答案)
文档属性
| 名称 | 湖北省宜昌市宜都市重点中学2023-2024学年高二上学期期中考试数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 901.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 22:33:10 | ||
图片预览




文档简介
宜都市重点中学2023-2024学年高二上学期期中考试
数学
一 单选题:本大题共8小题,每小题5分,共计40分.每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知,则( )
A.-19 B.-20 C.20 D.19
2.在空间直角坐标系中,点关于平面对称的点坐标是( )
A. B.
C. D.
3.从装有除颜色外完全相同的2个红球(编号为1,2)和2个白球(编号为1,2)的口袋内任取2个球,那么互斥而不对立的两个随机事件是( )
A.至少有1个白球,都是白球
B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球
D.至少有1个白球,都是红球
4.已知一组数据从小到大为,若这组数据的分位数是中位数的两倍,则( )
A.12 B.11 C.10 D.9
5.已知直线与直线平行,则( )
A.0 B.0或 C. D.0或
6.若方程表示圆,则的取值范围是( )
A. B. C. D.
7.两定点的距离为3,动点满足,则点的轨迹长为( )
A. B. C. D.
8.若直线:平分圆的面积,则的最小值为( ).
A.6 B.8 C.4 D.
二 多选题:本大题共4小题,每小题5分,共计20分.每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,选对但不全得2分,有选错的得0分.
9.已知直线的一个方向向量为,且经过点,则下列结论中正确的是( )
A.的倾斜角等于
B.在轴上的截距等于
C.与直线垂直
D.与直线平行
10.某商场推出二次开奖活动,凡购买一定价值的商品可以获得一张奖券,奖券上有一个兄奖号码,可以分别参加两次抽奖方式相同的兑奖活动.如果每次兑奖活动中奖概率都是0.05,且每次中奖互不影响,则两次抽奖中( )
A.都中奖的概率为0.05
B.都没有中奖的概率为0.95
C.恰有一次中奖的概率为0.095
D.至少有一次中奖的概率为0.0975
11.设有一组圆,下列命题正确的是( )
A.不论如何变化,圆心始终在一条直线上
B.所有圆均不经过点
C.经过点的圆有且只有一个
D.所有圆的面积均为
12.如图,正方体的棱长为分别为的中点,则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点与点到平面的距离相等
三 填空题:本大题共4小题,每小题5分,共计20分.
13.平行线与间的距离为__________.
14.已知,若四点共面,则__________.
15.已知棱长为1的正方体为的中点,点为四边形及其内部任意一点,若,则三棱锥体积的取值范围是__________.
16.点在动直线上的投影为点,若点,那么的最小值为__________.
四 解答题:本大题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
已知.
(1)求点到直线的距离;
(2)求的外接圆的方程.
18.(12分)
如图,二面角的大小为,四边形与均为正方形,,,记.
(1)请用表示,并求;
(2)求异面直线与所成角的余弦值.
19.(12分)
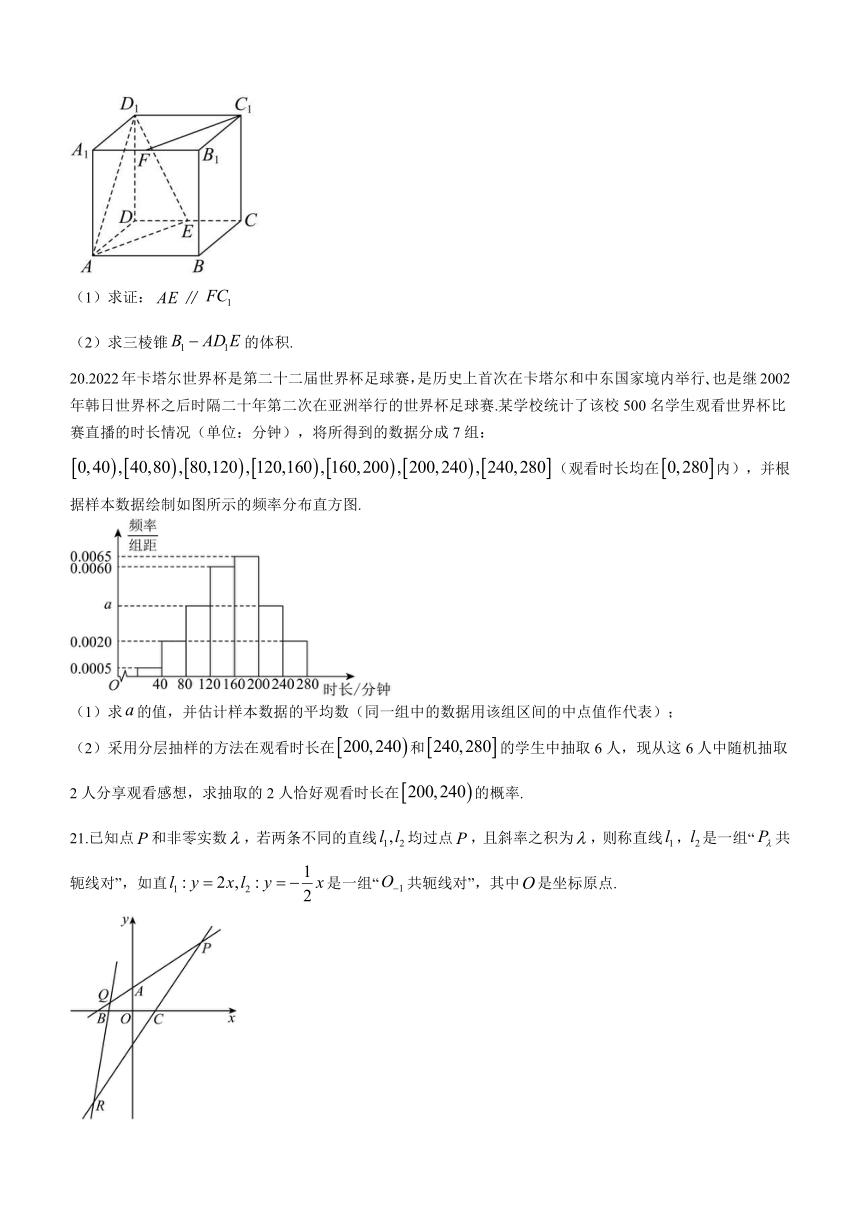
如图,在棱长为2的正方体中,点分别是线段的中点.
(1)求证:
(2)求三棱锥的体积.
20.2022年卡塔尔世界杯是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行 也是继2002年韩日世界杯之后时隔二十年第二次在亚洲举行的世界杯足球赛.某学校统计了该校500名学生观看世界杯比赛直播的时长情况(单位:分钟),将所得到的数据分成7组:(观看时长均在内),并根据样本数据绘制如图所示的频率分布直方图.
(1)求的值,并估计样本数据的平均数(同一组中的数据用该组区间的中点值作代表);
(2)采用分层抽样的方法在观看时长在和的学生中抽取6人,现从这6人中随机抽取2人分享观看感想,求抽取的2人恰好观看时长在的概率.
21.已知点和非零实数,若两条不同的直线均过点,且斜率之积为,则称直线,是一组“共轭线对”,如直是一组“共轭线对”,其中是坐标原点.
(1)已知点 点和点分别是三条直线上的点(与均不重合),且直线是“共轭线对”,直线是“共轭线对”,直线是“共轭线对”,求点的坐标;
(2)已知点,直线是“共轭线对”,当的斜率变化时,求原点到直线的距离之积的取值范围.
22.如图,在八面体中,四边形是边长为2的正方形,平面平面,二面角与二面角的大小都是.
(1)证明:平面平面;
(2)设为的重心,是否在棱上存在点,使得与平面所成角的正弦值为,若存在,求到平面的距离,若不存在,请说明理由.
宜都市重点中学2023-2024学年高二上学期期中考试
数学参考答案
1-4DACC 5-8CAAB
9.CD 10.CD 11.ABD 12.BC
13. 14.5 15. 16.
17.【详解】(1)直线的方程为,
化简可得,
所以点到直线的距离.
(2)设的外接圆的方程为,
将的坐标代入,得
,即
解得;
故所求圆的方程为.
18.【详解】(1)由已知得:,
,
∴,
∴
(2)四边形与均为正方形,平面平面,
所以即二面角的大小为,且
∴,
∴===,
∴异面直线AB与PQ所成角的余弦值为.
19.【详解】(1)建立如图所示的空间直角坐标系,
,
所以,显然,易知两者不共线,
所以有;
(2)由(1)可得:,
所以,
设平面的法向量为,
所以有,
因此点到平面的距离为,
在等腰三角形中,,
所以等腰三角形的面积为,
所以三棱锥的体积为
20.【详解】(1)解:由频率分布直方图性质得:
,
解得
平均数为
,
∴估计样本数据的平均数为157.6;
(2)解:采用以样本量比例分配的分层随机抽样方式,
则中抽取人,
分别记为,,,,中抽取人,分别记为,,
现从这6人中随机抽取2人分享观看感想,包含的基本事件有:
,,,,,,,,,,,,,,共15个,
抽取的2人恰好观看时长在基本事件有:
,,,,,共6个,
所以抽取的3人中恰有2人的观看时长在的概率为.
21.【详解】(1)设直线RP,PQ,QR的斜率分别为,,,
则,得,,或,,.
当,,时,直线RP的方程为,直线PQ的方程为,
由,解得,则;
当,,时,直线PR的方程为,直线PQ的方程为,
由,解得,则;
故所求为或;
(2)设:,:,其中,
故
由于(等号成立的条件是),
故,.
22.【详解】(1)因为为正方形,所以,又,,平面,
所以平面,所以为二面角的平面角,即,
又平面平面,,
所以平面,即为二面角的平面角,即,
如图建立空间直角坐标系,则,,,,
所以,,即,所以,
因为平面,平面,所以平面,
又,平面,平面,所以平面,
因为,平面,
所以平面平面.
(2)由点在上,设点,其中,点,
所以,平面的法向量可以为,
设与平面所成角为,
则,
即,化简得,
解得或(舍去),
所以存在点满足条件,且点到平面的距离为
数学
一 单选题:本大题共8小题,每小题5分,共计40分.每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.
1.已知,则( )
A.-19 B.-20 C.20 D.19
2.在空间直角坐标系中,点关于平面对称的点坐标是( )
A. B.
C. D.
3.从装有除颜色外完全相同的2个红球(编号为1,2)和2个白球(编号为1,2)的口袋内任取2个球,那么互斥而不对立的两个随机事件是( )
A.至少有1个白球,都是白球
B.至少有1个白球,至少有1个红球
C.恰有1个白球,恰有2个白球
D.至少有1个白球,都是红球
4.已知一组数据从小到大为,若这组数据的分位数是中位数的两倍,则( )
A.12 B.11 C.10 D.9
5.已知直线与直线平行,则( )
A.0 B.0或 C. D.0或
6.若方程表示圆,则的取值范围是( )
A. B. C. D.
7.两定点的距离为3,动点满足,则点的轨迹长为( )
A. B. C. D.
8.若直线:平分圆的面积,则的最小值为( ).
A.6 B.8 C.4 D.
二 多选题:本大题共4小题,每小题5分,共计20分.每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,选对但不全得2分,有选错的得0分.
9.已知直线的一个方向向量为,且经过点,则下列结论中正确的是( )
A.的倾斜角等于
B.在轴上的截距等于
C.与直线垂直
D.与直线平行
10.某商场推出二次开奖活动,凡购买一定价值的商品可以获得一张奖券,奖券上有一个兄奖号码,可以分别参加两次抽奖方式相同的兑奖活动.如果每次兑奖活动中奖概率都是0.05,且每次中奖互不影响,则两次抽奖中( )
A.都中奖的概率为0.05
B.都没有中奖的概率为0.95
C.恰有一次中奖的概率为0.095
D.至少有一次中奖的概率为0.0975
11.设有一组圆,下列命题正确的是( )
A.不论如何变化,圆心始终在一条直线上
B.所有圆均不经过点
C.经过点的圆有且只有一个
D.所有圆的面积均为
12.如图,正方体的棱长为分别为的中点,则( )
A.直线与直线垂直
B.直线与平面平行
C.平面截正方体所得的截面面积为
D.点与点到平面的距离相等
三 填空题:本大题共4小题,每小题5分,共计20分.
13.平行线与间的距离为__________.
14.已知,若四点共面,则__________.
15.已知棱长为1的正方体为的中点,点为四边形及其内部任意一点,若,则三棱锥体积的取值范围是__________.
16.点在动直线上的投影为点,若点,那么的最小值为__________.
四 解答题:本大题共6小题,共70分.解答应写出文字说明 证明过程或演算步骤.
17.(10分)
已知.
(1)求点到直线的距离;
(2)求的外接圆的方程.
18.(12分)
如图,二面角的大小为,四边形与均为正方形,,,记.
(1)请用表示,并求;
(2)求异面直线与所成角的余弦值.
19.(12分)
如图,在棱长为2的正方体中,点分别是线段的中点.
(1)求证:
(2)求三棱锥的体积.
20.2022年卡塔尔世界杯是第二十二届世界杯足球赛,是历史上首次在卡塔尔和中东国家境内举行 也是继2002年韩日世界杯之后时隔二十年第二次在亚洲举行的世界杯足球赛.某学校统计了该校500名学生观看世界杯比赛直播的时长情况(单位:分钟),将所得到的数据分成7组:(观看时长均在内),并根据样本数据绘制如图所示的频率分布直方图.
(1)求的值,并估计样本数据的平均数(同一组中的数据用该组区间的中点值作代表);
(2)采用分层抽样的方法在观看时长在和的学生中抽取6人,现从这6人中随机抽取2人分享观看感想,求抽取的2人恰好观看时长在的概率.
21.已知点和非零实数,若两条不同的直线均过点,且斜率之积为,则称直线,是一组“共轭线对”,如直是一组“共轭线对”,其中是坐标原点.
(1)已知点 点和点分别是三条直线上的点(与均不重合),且直线是“共轭线对”,直线是“共轭线对”,直线是“共轭线对”,求点的坐标;
(2)已知点,直线是“共轭线对”,当的斜率变化时,求原点到直线的距离之积的取值范围.
22.如图,在八面体中,四边形是边长为2的正方形,平面平面,二面角与二面角的大小都是.
(1)证明:平面平面;
(2)设为的重心,是否在棱上存在点,使得与平面所成角的正弦值为,若存在,求到平面的距离,若不存在,请说明理由.
宜都市重点中学2023-2024学年高二上学期期中考试
数学参考答案
1-4DACC 5-8CAAB
9.CD 10.CD 11.ABD 12.BC
13. 14.5 15. 16.
17.【详解】(1)直线的方程为,
化简可得,
所以点到直线的距离.
(2)设的外接圆的方程为,
将的坐标代入,得
,即
解得;
故所求圆的方程为.
18.【详解】(1)由已知得:,
,
∴,
∴
(2)四边形与均为正方形,平面平面,
所以即二面角的大小为,且
∴,
∴===,
∴异面直线AB与PQ所成角的余弦值为.
19.【详解】(1)建立如图所示的空间直角坐标系,
,
所以,显然,易知两者不共线,
所以有;
(2)由(1)可得:,
所以,
设平面的法向量为,
所以有,
因此点到平面的距离为,
在等腰三角形中,,
所以等腰三角形的面积为,
所以三棱锥的体积为
20.【详解】(1)解:由频率分布直方图性质得:
,
解得
平均数为
,
∴估计样本数据的平均数为157.6;
(2)解:采用以样本量比例分配的分层随机抽样方式,
则中抽取人,
分别记为,,,,中抽取人,分别记为,,
现从这6人中随机抽取2人分享观看感想,包含的基本事件有:
,,,,,,,,,,,,,,共15个,
抽取的2人恰好观看时长在基本事件有:
,,,,,共6个,
所以抽取的3人中恰有2人的观看时长在的概率为.
21.【详解】(1)设直线RP,PQ,QR的斜率分别为,,,
则,得,,或,,.
当,,时,直线RP的方程为,直线PQ的方程为,
由,解得,则;
当,,时,直线PR的方程为,直线PQ的方程为,
由,解得,则;
故所求为或;
(2)设:,:,其中,
故
由于(等号成立的条件是),
故,.
22.【详解】(1)因为为正方形,所以,又,,平面,
所以平面,所以为二面角的平面角,即,
又平面平面,,
所以平面,即为二面角的平面角,即,
如图建立空间直角坐标系,则,,,,
所以,,即,所以,
因为平面,平面,所以平面,
又,平面,平面,所以平面,
因为,平面,
所以平面平面.
(2)由点在上,设点,其中,点,
所以,平面的法向量可以为,
设与平面所成角为,
则,
即,化简得,
解得或(舍去),
所以存在点满足条件,且点到平面的距离为
同课章节目录
