专题18.58平行四边形 全章复习与巩固 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.58平行四边形 全章复习与巩固 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |  | |
| 格式 | docx | ||
| 文件大小 | 986.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 22:22:59 | ||
图片预览



文档简介
专题 18.58 平行四边形(全章复习与巩固)
(基础篇)(专项练习)
一、单选题
1.如图,在中,,则的度数是( )
A. B. C. D.
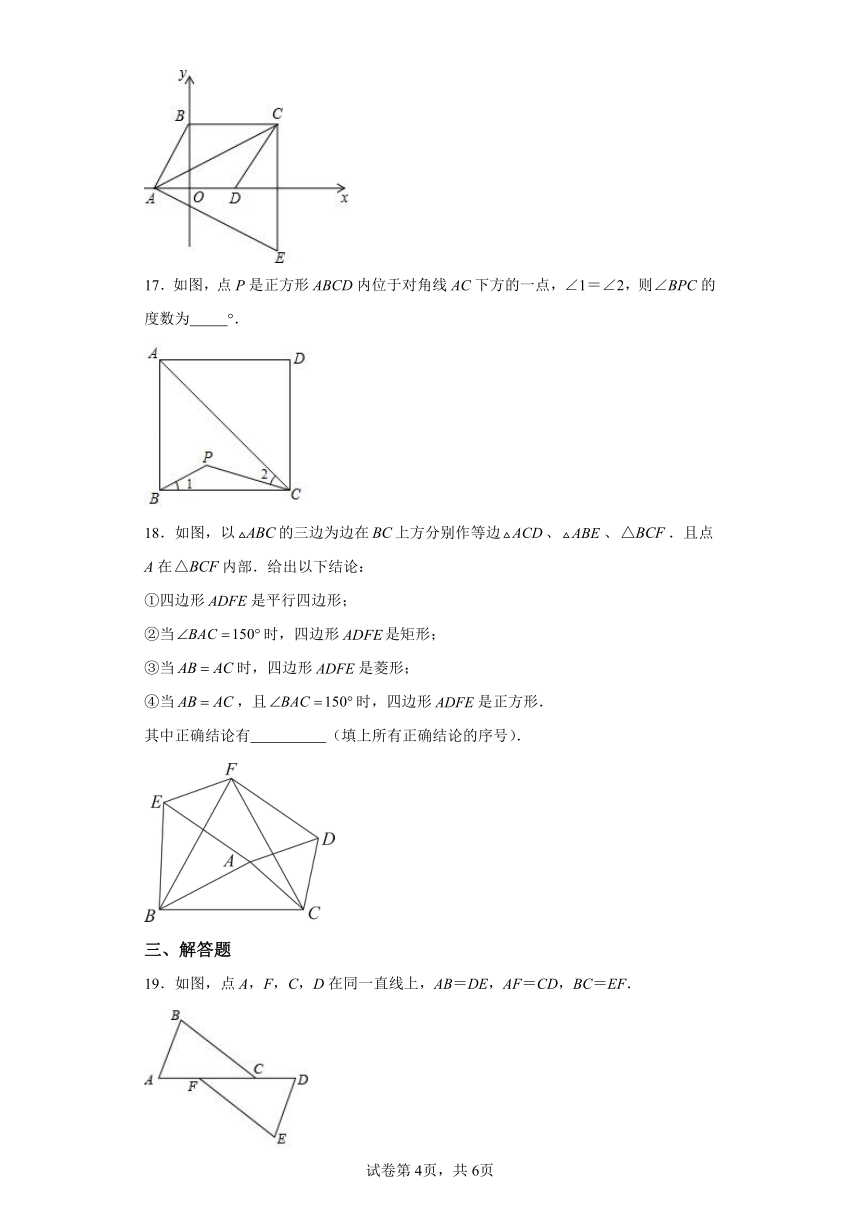
2.如图,在平行四边形中,,,,平分,下列结论错误的是( )
A. B. C. D.
3.已知矩形的两条对角线、相交于点O,则下列结论不一定正确的是( )
A. B. C. D.
4.两个矩形的位置如图所示,若则的度数为( )
A. B. C. D.
5.菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )
A.3:1 B.4:1 C.5:1 D.6:1
6.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
7.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8.已知四边形是平行四边形,下列结论中错误的有( )
①当时,它是菱形;
②当时,它是菱形;
③当时,它是矩形;
④当时,它是正方形.
A.1个 B.2个 C.3个 D.4个
9.如图所示,正方形的面积为12,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A. B. C. D.
10.如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接.已知∠C=120°,∠BAE=50°,则的度数为( )
A.50° B.60° C.80° D.90°
二、填空题
11.如图,在中,,,D是的中点,则 °.
12.已知矩形的一边长为,一条对角线的长为,则矩形的面积为 .
13.如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.
14.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为 (结果保留很号).
15.小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
16.如图,在平面直角坐标系中,是以菱形的对角线为边的等边三角形,点与点关于轴对称,则点的坐标是 .
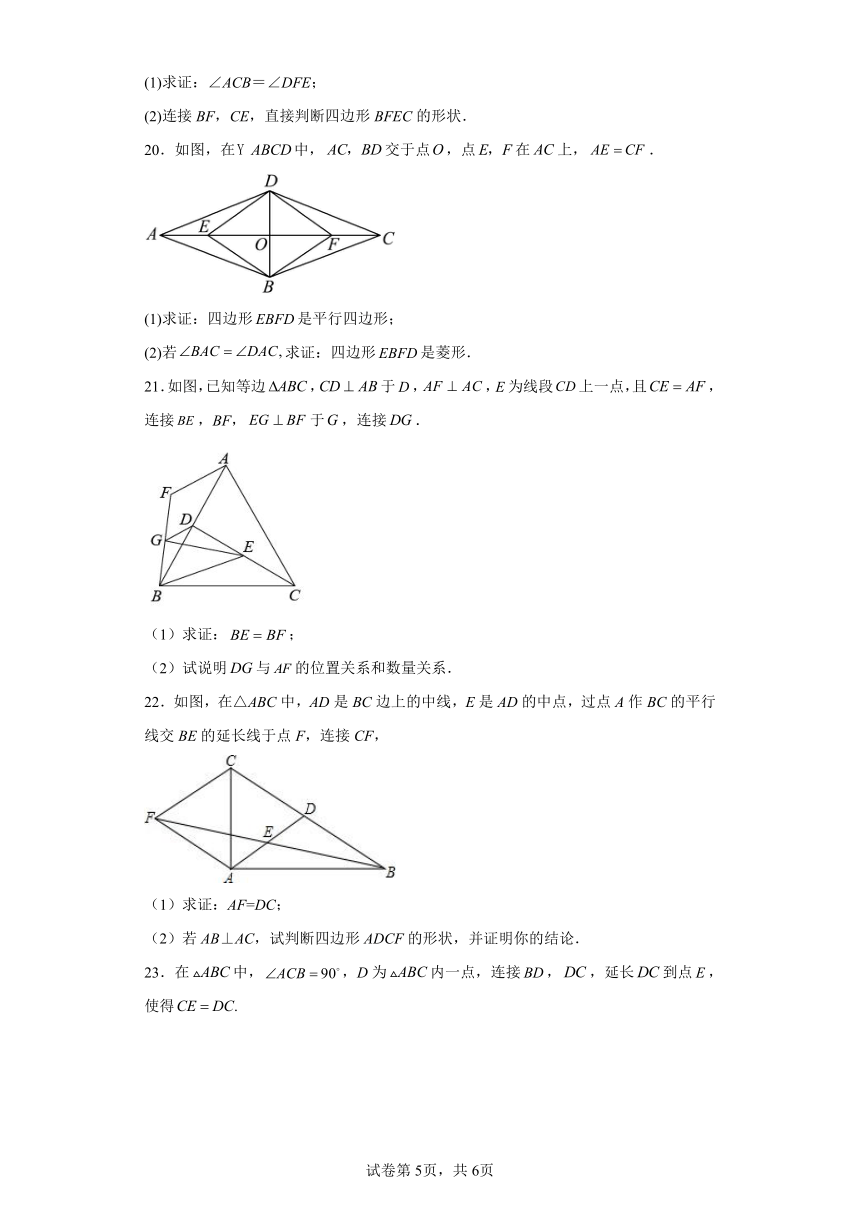
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
18.如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当,且时,四边形是正方形.
其中正确结论有 (填上所有正确结论的序号).
三、解答题
19.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
20.如图,在中,交于点,点在上,.
(1)求证:四边形是平行四边形;
(2)若求证:四边形是菱形.
21.如图,已知等边,于,,为线段上一点,且,连接,BF,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
22.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF,
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
23.在中,,D为内一点,连接,,延长到点,使得
(1)如图1,延长到点,使得,连接,,若,求证:;
(2)连接,交的延长线于点,连接,依题意补全图2,若,用等式表示线段与的数量关系,并证明.
24.如图,在巾,,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将沿AD折叠得到,连接BE.
(1)当时,___________;
(2)探究与之间的数量关系,并给出证明;
(3)设,的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据平行四边形的性质,得出,再根据平行线的性质,得出,与题意联立方程组,解出即可得出答案.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∴可得:,
解得:,
∴的度数为.
故选:B
【点睛】本题考查了平行四边形的性质、平行线的性质、解二元一次方程组,解本题的关键在得出.
2.C
【分析】根据平行四边形的性质逐项分析判断即可求解,
【详解】解:四边形是平行四边形,,
,,,,
,故D正确;
平分,
,
,
,故C错误;
,
,故A正确;
,
,故B正确.
故选:C.
【点睛】本题考查了平行四边形的性质,角平分线的定义,掌握平行四边形的性质是解题的关键.
3.A
【分析】根据矩形的性质解答即可.
【详解】解:如图所示,
在矩形中,,,,
故B、C、D选项结论正确,
当四边形为菱形或正方形时,成立,
故结论不一定正确的是A选项,
故选:A.
【点睛】本题考查了矩形的性质,矩形的对边互相平行且相等,四个内角都是直角,对角线互相平分且相等.
4.C
【分析】由补角的定义可得,由题意可得,,则有,即可得解.
【详解】解:如图,
由题意得:,
∵,
∴,
∴.
故选:C.
【点睛】本题主要考查矩形的性质,余角与补角,解答的关键是明确互余的两角之和为90°,互补的两角之和为180°
5.C
【详解】如图所示,
∵菱形的周长为8cm,
∴菱形的边长为2cm,
∵菱形的高为1cm,
∴sinB=
∴∠B=30°,
∴∠C=150°,
则该菱形两邻角度数比为5:1,
故选C.
6.D
【分析】根据菱形的性质利用勾股定理求得的长,从而得到的长,再根据菱形的面积公式即可求得其面积.
【详解】解:∵四边形是菱形,,
∴,,
∵在中, ,
∴,
∴,
∴.
故选D.
【点睛】此题考查学生对菱形的性质及勾股定理的理解及运用,熟练掌握菱形的性质是解答本题的关键.
7.B
【详解】解:∵分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故选:B.
8.B
【分析】根据矩形、菱形、正方形的判定逐一判断各项即可得出答案.
【详解】解:∵四边形是平行四边形,
∴当时,不能判断它是菱形(对边相等是平行四边形的性质),故①错误,
当时,它是菱形,故②正确,
当时,它是矩形,故③正确,
当时,它是矩形,故④错误,
故选:B.
【点睛】本题考查了矩形、菱形、正方形的判定,熟练掌握性质定理是解题的关键.
9.B
【分析】连接,,根据点B与D关于对称,得出,从而得出,即最小值为值为的长,求出的长即可.
【详解】解:连接,,如图所示:
∵四边形为正方形,
∴点B与D关于对称,
∴,
∴,
∴最小值为的长,
∵正方形的面积为12,
∴,
又∵是等边三角形,
∴,
∴最小值为,故B正确.
故选:B.
【点睛】本题主要考查了正方形的性质,轴对称的性质,等边三角形的性质,解题的关键是根据轴对称的性质得出的长为的最小值.
10.C
【分析】由翻折的性质知∠BAE==50°,=AB,再由菱形的性质得∠BAD=120°,=AD,最后利用三角形内角和定理可得答案.
【详解】解:∵四边形ABCD是菱形,∠C=120°,
∴∠BAD=∠C=120°,AB=AD,
∵将△ABE沿直线AE翻折,使点B落在上,
∴∠BAE==50°,=AB,
∴=100°,=AD,
∴=20°,
∴==(180°-20°)÷2=80°,
故选:C.
【点睛】本题主要考查了菱形的性质,翻折的性质,三角形内角和定理等知识,求出=20°是解题的关键.
11.36
【分析】由“直角三角形的两个锐角互余”得到.根据“直角三角形斜边上的中线等于斜边的一半”得到,则等边对等角求得.
【详解】解:∵在中,,,
∴,
∵D为线段的中点,
∴,
∴,
故答案为:36.
【点睛】本题考查了直角三角形的性质.解题关键是熟练掌握在直角三角形中,斜边上的中线等于斜边的一半.
12.48
【分析】如图,先根据勾股定理求出,再由求解即可.
【详解】解:在矩形ABCD中,,,
∴在中,(cm),
∴.
故答案为:48.
【点睛】此题考查了矩形的性质,勾股定理,解题的关键是熟知上述知识.
13.3
【详解】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵AC+BD=24厘米,
∴OA+OB=12厘米.
∵△OAB的周长是18厘米,
∴AB=6厘米.
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线.
∴EF=AB=3厘米.
故答案为:3
14.
【分析】连接AC交BD于H,证明△DCH≌△DCF,得出DH的长度,再根据菱形的性质得出BD的长度.
【详解】解:如图,连接AC交BD于点H,
由菱形的性质得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°,
又∵∠ECM=30°,
∴∠DCF=50°,
∵DF⊥CM,
∴∠CFD=90°,
∴∠CDF=40°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=40°,
在△CDH和△CDF中,,
∴△CDH≌△CDF(AAS),
∴DH=DF=,
∴DB=2DH=.
故答案为:.
【点睛】本题主要考查菱形的性质和全等三角形的判定,菱形的对角线互相平分是此题的关键知识点,得出∠HDC=∠FDC是这个题最关键的一点.
15.
【分析】判定△AB′D′是等腰直角三角形,即可得出AB′=AD,再根据AB′= AB,再计算即可得到结论.
【详解】解:∵四边形ABCD是矩形,
∴∠D=∠B=∠DAB=90°,
由操作一可知:∠DAB′=∠D′AB′=45°,∠AD′B′=∠D=90°,AD=AD′,
∴△AB′D′是等腰直角三角形,
∴AD=AD′= B′D′,
由勾股定理得AB′=AD,
又由操作二可知:AB′=AB,
∴AD=AB,
∴=,
∴A4纸的长AB与宽AD的比值为.
故答案为:.
【点睛】本题主要考查了矩形的性质以及折叠变换的运用,解题的关键是理解题意,灵活运用所学知识解决问题.
16.
【分析】根据菱形的性质和等腰三角形的性质,进行计算,即可得到答案.
【详解】解:如图:
∵点与点关于轴对称,
∴,,
是以菱形的对角线为边的等边三角形,,
,
,
在菱形中,,,
∴,,
∴,
在中,,∴,
∴
又∵,
∴
∴,
,
点的坐标是.
故答案为.
【点睛】本题考查菱形的性质和平面直角坐标系,解题的关键是熟练掌握菱形的性质和平面直角坐标系.
17.135
【分析】由正方形的性质可得∠ACB=∠BAC=45°,可得∠2+∠BCP=45°=∠1+∠BCP,由三角形内角和定理可求解.
【详解】解:∵四边形ABCD是正方形
∴∠ACB=∠BAC=45°
∴∠2+∠BCP=45°
∵∠1=∠2
∴∠1+∠BCP=45°
∵∠BPC=180°﹣∠1﹣∠BCP
∴∠BPC=135°
故答案为:135.
【点睛】本题考查了正方形的性质,三角形内角和定理,掌握正方形的性质是本题的关键.
18.①②③④
【分析】对于结论①,由等边三角形的性质可得,,则;同理,由,得,由,即可得出四边形是平行四边形;对于结论②,当时,
,结合结论①,可知结论②正确;对于结论③,当时,,结合结论①,可知结论③正确;对于结论④,综合②③的结论知:当,且时,四边形既是菱形,又是矩形,故结论④正确.
【详解】解析:①、是等边三角形,
,,,
,
,
,
同理由,得,
由,即可得出四边形是平行四边形,故结论①正确;
②当时,
,
由①知四边形是平行四边形,
平行四边形是矩形,故结论②正确;
③由①知,,四边形是平行四边形,
当时,,
平行四边形是菱形,故结论③正确;
④综合②③的结论知:当,且时,四边形既是菱形,又是矩形,
四边形是正方形,故结论④正确.
故答案为:①②③④.
【点睛】本题主要考查了平行四边形、菱形、矩形、正方形的判定方法,熟练掌握以上图形的判定方法是解题的关键.
19.(1)见解析
(2)四边形BFEC是平行四边形
【分析】(1)证△ABC≌△DEF(SSS),再由全等三角形的性质即可得出结论;
(2)由(1)可知,∠ACB=∠DFE,则BC∥EF,再由平行四边形的判定即可得出结论.
【详解】(1)证明:∵AF=CD,
∴AF + CF = CD + CF,
即AC=DF,
在△ABC和△DEF中,
△ABC≌△DEF(SSS)
(2)如图,四边形BFEC是平行四边形,理由如下:
由(1)可知,∠ACB=∠DFE,
∴BC EF,
又∶ BC = EF,
四边形BFEC是平行四边形.
【点睛】本题考查了平行网边形的判定、全等三角形的判定与性质、平行线的判定等知识,熟练掌握平行四边形的判定方法,证明三角形全等是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1)先根据四边形ABCD为平行四边形,得出,,再根据,得出,即可证明结论;
(2)先证明,得出,证明四边形ABCD为菱形,得出,即可证明结论.
【详解】(1)证明:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
即,
∴四边形是平行四边形.
(2)∵四边形ABCD为平行四边形,
∴,
∴,
∵
∴,
∴,
∴四边形ABCD为菱形,
∴,
即,
∵四边形是平行四边形,
∴四边形是菱形.
【点睛】本题主要考查了平行四边形的判定和性质,菱形的判定和性质,平行线的性质,熟练掌握菱形和平行四边形的判定方法,是解题的关键.
21.(1)详见解析;(2),,理由详见解析.
【分析】(1)由等边三角形的性质可得,,,,由“”可证,可得;
(2)由可得,进而可得,由即可证明是等边三角形,可得,由三角形中位线定理可得,.
【详解】(1)∵是等边三角形,
,,
∵,,
∴,,
∵,
,
,
,且,,
,
,
(2),.理由如下:
连接,
∵
∴,
∵,
∴,
∵,
是等边三角形,
∵,
,且,
,.
【点睛】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,三角形中位线定理,熟练运用三角形中位线定理是本题的关键.
22.(1)见解析(2)见解析
【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案.
(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
【详解】解:(1)证明:∵AF∥BC,
∴∠AFE=∠DBE.
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD.
在△AFE和△DBE中,
∵∠AFE=∠DBE,∠FEA=∠BED, AE=DE,
∴△AFE≌△DBE(AAS)
∴AF=BD.
∴AF=DC.
(2)四边形ADCF是菱形,证明如下:
∵AF∥BC,AF=DC,
∴四边形ADCF是平行四边形.
∵AC⊥AB,AD是斜边BC的中线,
∴AD=DC.
∴平行四边形ADCF是菱形.
23.(1)见解析
(2);证明见解析
【分析】(1)先利用已知条件证明,得出,推出,再由即可证明;
(2)延长BC到点M,使CM=CB,连接EM,AM,先证,推出,通过等量代换得到,利用平行线的性质得出,利用直角三角形斜边中线等于斜边一半即可得到.
【详解】(1)证明:在和中,
,
∴ ,
∴ ,
∴ ,
∵,
∴.
(2)解:补全后的图形如图所示,,证明如下:
延长BC到点M,使CM=CB,连接EM,AM,
∵,CM=CB,
∴ 垂直平分BM,
∴,
在和中,
,
∴ ,
∴ ,,
∵,
∴ ,
∴ ,
∵,
∴,
∴ ,即,
∵,
∴ ,
∴ .
【点睛】本题考查全等三角形的判定与性质,垂直平分线的性质,平行线的判定与性质,勾股定理的逆用,直角三角形斜边中线的性质等,第二问有一定难度,正确作辅助线,证明是解题的关键.
24.(1)
(2)
(3)
【分析】(1)首先由折叠的性质可得,再由等腰三角形的性质可求解;
(2)首先由折叠的性质可得,,再由等腰三角形的性质可得,,最后根据角度关系即可求解;
(3)首先由等腰直角三角形的性质和直角三角形的性质可求的长,由勾股定理可求的长,最后根据面积和差关系可求解.
【详解】(1),,,
,
将沿折叠得到,
,
,
∴△ABE是等边三角形,
,
故答案为:60;
(2),理由如下:
将沿折叠得到,
,,
,,
,
,
,
;
(3)如图,连接,
,点是的中点,
,
,,
,,
,
,
,
,
.
【点睛】本题考查了等腰直角三角形的性质,直角三角形的性质,折叠的性质等知识,解题的关键是熟练掌握相关性质并能够灵活运用.
答案第1页,共2页
答案第1页,共2页
(基础篇)(专项练习)
一、单选题
1.如图,在中,,则的度数是( )
A. B. C. D.
2.如图,在平行四边形中,,,,平分,下列结论错误的是( )
A. B. C. D.
3.已知矩形的两条对角线、相交于点O,则下列结论不一定正确的是( )
A. B. C. D.
4.两个矩形的位置如图所示,若则的度数为( )
A. B. C. D.
5.菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为( )
A.3:1 B.4:1 C.5:1 D.6:1
6.已知在菱形中,,,则菱形的面积为( )
A.160 B.80 C.40 D.96
7.如图,小聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
A.矩形 B.菱形 C.正方形 D.等腰梯形
8.已知四边形是平行四边形,下列结论中错误的有( )
①当时,它是菱形;
②当时,它是菱形;
③当时,它是矩形;
④当时,它是正方形.
A.1个 B.2个 C.3个 D.4个
9.如图所示,正方形的面积为12,是等边三角形,点E在正方形内,在对角线上有一点P,使的和最小,则这个最小值为( )
A. B. C. D.
10.如图,在菱形纸片ABCD中,E是BC边上一点,将△ABE沿直线AE翻折,使点B落在上,连接.已知∠C=120°,∠BAE=50°,则的度数为( )
A.50° B.60° C.80° D.90°
二、填空题
11.如图,在中,,,D是的中点,则 °.
12.已知矩形的一边长为,一条对角线的长为,则矩形的面积为 .
13.如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.
14.如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF=,则BD的长为 (结果保留很号).
15.小莹按照如图所示的步骤折叠A4纸,折完后,发现折痕AB′与A4纸的长边AB恰好重合,那么A4纸的长AB与宽AD的比值为 .
16.如图,在平面直角坐标系中,是以菱形的对角线为边的等边三角形,点与点关于轴对称,则点的坐标是 .
17.如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
18.如图,以的三边为边在上方分别作等边、、.且点A在内部.给出以下结论:
①四边形是平行四边形;
②当时,四边形是矩形;
③当时,四边形是菱形;
④当,且时,四边形是正方形.
其中正确结论有 (填上所有正确结论的序号).
三、解答题
19.如图,点A,F,C,D在同一直线上,AB=DE,AF=CD,BC=EF.
(1)求证:∠ACB=∠DFE;
(2)连接BF,CE,直接判断四边形BFEC的形状.
20.如图,在中,交于点,点在上,.
(1)求证:四边形是平行四边形;
(2)若求证:四边形是菱形.
21.如图,已知等边,于,,为线段上一点,且,连接,BF,于,连接.
(1)求证:;
(2)试说明与的位置关系和数量关系.
22.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF,
(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
23.在中,,D为内一点,连接,,延长到点,使得
(1)如图1,延长到点,使得,连接,,若,求证:;
(2)连接,交的延长线于点,连接,依题意补全图2,若,用等式表示线段与的数量关系,并证明.
24.如图,在巾,,点O为BC的中点,点D是线段OC上的动点(点D不与点O,C重合),将沿AD折叠得到,连接BE.
(1)当时,___________;
(2)探究与之间的数量关系,并给出证明;
(3)设,的面积为x,以AD为边长的正方形的面积为y,求y关于x的函数解析式.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据平行四边形的性质,得出,再根据平行线的性质,得出,与题意联立方程组,解出即可得出答案.
【详解】解:∵四边形是平行四边形,
∴,
∴,
∴可得:,
解得:,
∴的度数为.
故选:B
【点睛】本题考查了平行四边形的性质、平行线的性质、解二元一次方程组,解本题的关键在得出.
2.C
【分析】根据平行四边形的性质逐项分析判断即可求解,
【详解】解:四边形是平行四边形,,
,,,,
,故D正确;
平分,
,
,
,故C错误;
,
,故A正确;
,
,故B正确.
故选:C.
【点睛】本题考查了平行四边形的性质,角平分线的定义,掌握平行四边形的性质是解题的关键.
3.A
【分析】根据矩形的性质解答即可.
【详解】解:如图所示,
在矩形中,,,,
故B、C、D选项结论正确,
当四边形为菱形或正方形时,成立,
故结论不一定正确的是A选项,
故选:A.
【点睛】本题考查了矩形的性质,矩形的对边互相平行且相等,四个内角都是直角,对角线互相平分且相等.
4.C
【分析】由补角的定义可得,由题意可得,,则有,即可得解.
【详解】解:如图,
由题意得:,
∵,
∴,
∴.
故选:C.
【点睛】本题主要考查矩形的性质,余角与补角,解答的关键是明确互余的两角之和为90°,互补的两角之和为180°
5.C
【详解】如图所示,
∵菱形的周长为8cm,
∴菱形的边长为2cm,
∵菱形的高为1cm,
∴sinB=
∴∠B=30°,
∴∠C=150°,
则该菱形两邻角度数比为5:1,
故选C.
6.D
【分析】根据菱形的性质利用勾股定理求得的长,从而得到的长,再根据菱形的面积公式即可求得其面积.
【详解】解:∵四边形是菱形,,
∴,,
∵在中, ,
∴,
∴,
∴.
故选D.
【点睛】此题考查学生对菱形的性质及勾股定理的理解及运用,熟练掌握菱形的性质是解答本题的关键.
7.B
【详解】解:∵分别以A和B为圆心,大于AB的长为半径画弧,两弧相交于C、D,
∴AC=AD=BD=BC,
∴四边形ADBC一定是菱形,
故选:B.
8.B
【分析】根据矩形、菱形、正方形的判定逐一判断各项即可得出答案.
【详解】解:∵四边形是平行四边形,
∴当时,不能判断它是菱形(对边相等是平行四边形的性质),故①错误,
当时,它是菱形,故②正确,
当时,它是矩形,故③正确,
当时,它是矩形,故④错误,
故选:B.
【点睛】本题考查了矩形、菱形、正方形的判定,熟练掌握性质定理是解题的关键.
9.B
【分析】连接,,根据点B与D关于对称,得出,从而得出,即最小值为值为的长,求出的长即可.
【详解】解:连接,,如图所示:
∵四边形为正方形,
∴点B与D关于对称,
∴,
∴,
∴最小值为的长,
∵正方形的面积为12,
∴,
又∵是等边三角形,
∴,
∴最小值为,故B正确.
故选:B.
【点睛】本题主要考查了正方形的性质,轴对称的性质,等边三角形的性质,解题的关键是根据轴对称的性质得出的长为的最小值.
10.C
【分析】由翻折的性质知∠BAE==50°,=AB,再由菱形的性质得∠BAD=120°,=AD,最后利用三角形内角和定理可得答案.
【详解】解:∵四边形ABCD是菱形,∠C=120°,
∴∠BAD=∠C=120°,AB=AD,
∵将△ABE沿直线AE翻折,使点B落在上,
∴∠BAE==50°,=AB,
∴=100°,=AD,
∴=20°,
∴==(180°-20°)÷2=80°,
故选:C.
【点睛】本题主要考查了菱形的性质,翻折的性质,三角形内角和定理等知识,求出=20°是解题的关键.
11.36
【分析】由“直角三角形的两个锐角互余”得到.根据“直角三角形斜边上的中线等于斜边的一半”得到,则等边对等角求得.
【详解】解:∵在中,,,
∴,
∵D为线段的中点,
∴,
∴,
故答案为:36.
【点睛】本题考查了直角三角形的性质.解题关键是熟练掌握在直角三角形中,斜边上的中线等于斜边的一半.
12.48
【分析】如图,先根据勾股定理求出,再由求解即可.
【详解】解:在矩形ABCD中,,,
∴在中,(cm),
∴.
故答案为:48.
【点睛】此题考查了矩形的性质,勾股定理,解题的关键是熟知上述知识.
13.3
【详解】∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
又∵AC+BD=24厘米,
∴OA+OB=12厘米.
∵△OAB的周长是18厘米,
∴AB=6厘米.
∵点E,F分别是线段AO,BO的中点,
∴EF是△OAB的中位线.
∴EF=AB=3厘米.
故答案为:3
14.
【分析】连接AC交BD于H,证明△DCH≌△DCF,得出DH的长度,再根据菱形的性质得出BD的长度.
【详解】解:如图,连接AC交BD于点H,
由菱形的性质得∠ADC=∠ABC=80°,∠DCE=80°,∠DHC=90°,
又∵∠ECM=30°,
∴∠DCF=50°,
∵DF⊥CM,
∴∠CFD=90°,
∴∠CDF=40°,
又∵四边形ABCD是菱形,
∴BD平分∠ADC,
∴∠HDC=40°,
在△CDH和△CDF中,,
∴△CDH≌△CDF(AAS),
∴DH=DF=,
∴DB=2DH=.
故答案为:.
【点睛】本题主要考查菱形的性质和全等三角形的判定,菱形的对角线互相平分是此题的关键知识点,得出∠HDC=∠FDC是这个题最关键的一点.
15.
【分析】判定△AB′D′是等腰直角三角形,即可得出AB′=AD,再根据AB′= AB,再计算即可得到结论.
【详解】解:∵四边形ABCD是矩形,
∴∠D=∠B=∠DAB=90°,
由操作一可知:∠DAB′=∠D′AB′=45°,∠AD′B′=∠D=90°,AD=AD′,
∴△AB′D′是等腰直角三角形,
∴AD=AD′= B′D′,
由勾股定理得AB′=AD,
又由操作二可知:AB′=AB,
∴AD=AB,
∴=,
∴A4纸的长AB与宽AD的比值为.
故答案为:.
【点睛】本题主要考查了矩形的性质以及折叠变换的运用,解题的关键是理解题意,灵活运用所学知识解决问题.
16.
【分析】根据菱形的性质和等腰三角形的性质,进行计算,即可得到答案.
【详解】解:如图:
∵点与点关于轴对称,
∴,,
是以菱形的对角线为边的等边三角形,,
,
,
在菱形中,,,
∴,,
∴,
在中,,∴,
∴
又∵,
∴
∴,
,
点的坐标是.
故答案为.
【点睛】本题考查菱形的性质和平面直角坐标系,解题的关键是熟练掌握菱形的性质和平面直角坐标系.
17.135
【分析】由正方形的性质可得∠ACB=∠BAC=45°,可得∠2+∠BCP=45°=∠1+∠BCP,由三角形内角和定理可求解.
【详解】解:∵四边形ABCD是正方形
∴∠ACB=∠BAC=45°
∴∠2+∠BCP=45°
∵∠1=∠2
∴∠1+∠BCP=45°
∵∠BPC=180°﹣∠1﹣∠BCP
∴∠BPC=135°
故答案为:135.
【点睛】本题考查了正方形的性质,三角形内角和定理,掌握正方形的性质是本题的关键.
18.①②③④
【分析】对于结论①,由等边三角形的性质可得,,则;同理,由,得,由,即可得出四边形是平行四边形;对于结论②,当时,
,结合结论①,可知结论②正确;对于结论③,当时,,结合结论①,可知结论③正确;对于结论④,综合②③的结论知:当,且时,四边形既是菱形,又是矩形,故结论④正确.
【详解】解析:①、是等边三角形,
,,,
,
,
,
同理由,得,
由,即可得出四边形是平行四边形,故结论①正确;
②当时,
,
由①知四边形是平行四边形,
平行四边形是矩形,故结论②正确;
③由①知,,四边形是平行四边形,
当时,,
平行四边形是菱形,故结论③正确;
④综合②③的结论知:当,且时,四边形既是菱形,又是矩形,
四边形是正方形,故结论④正确.
故答案为:①②③④.
【点睛】本题主要考查了平行四边形、菱形、矩形、正方形的判定方法,熟练掌握以上图形的判定方法是解题的关键.
19.(1)见解析
(2)四边形BFEC是平行四边形
【分析】(1)证△ABC≌△DEF(SSS),再由全等三角形的性质即可得出结论;
(2)由(1)可知,∠ACB=∠DFE,则BC∥EF,再由平行四边形的判定即可得出结论.
【详解】(1)证明:∵AF=CD,
∴AF + CF = CD + CF,
即AC=DF,
在△ABC和△DEF中,
△ABC≌△DEF(SSS)
(2)如图,四边形BFEC是平行四边形,理由如下:
由(1)可知,∠ACB=∠DFE,
∴BC EF,
又∶ BC = EF,
四边形BFEC是平行四边形.
【点睛】本题考查了平行网边形的判定、全等三角形的判定与性质、平行线的判定等知识,熟练掌握平行四边形的判定方法,证明三角形全等是解题的关键.
20.(1)见解析
(2)见解析
【分析】(1)先根据四边形ABCD为平行四边形,得出,,再根据,得出,即可证明结论;
(2)先证明,得出,证明四边形ABCD为菱形,得出,即可证明结论.
【详解】(1)证明:∵四边形ABCD为平行四边形,
∴,,
∵,
∴,
即,
∴四边形是平行四边形.
(2)∵四边形ABCD为平行四边形,
∴,
∴,
∵
∴,
∴,
∴四边形ABCD为菱形,
∴,
即,
∵四边形是平行四边形,
∴四边形是菱形.
【点睛】本题主要考查了平行四边形的判定和性质,菱形的判定和性质,平行线的性质,熟练掌握菱形和平行四边形的判定方法,是解题的关键.
21.(1)详见解析;(2),,理由详见解析.
【分析】(1)由等边三角形的性质可得,,,,由“”可证,可得;
(2)由可得,进而可得,由即可证明是等边三角形,可得,由三角形中位线定理可得,.
【详解】(1)∵是等边三角形,
,,
∵,,
∴,,
∵,
,
,
,且,,
,
,
(2),.理由如下:
连接,
∵
∴,
∵,
∴,
∵,
是等边三角形,
∵,
,且,
,.
【点睛】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,三角形中位线定理,熟练运用三角形中位线定理是本题的关键.
22.(1)见解析(2)见解析
【分析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案.
(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.
【详解】解:(1)证明:∵AF∥BC,
∴∠AFE=∠DBE.
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD.
在△AFE和△DBE中,
∵∠AFE=∠DBE,∠FEA=∠BED, AE=DE,
∴△AFE≌△DBE(AAS)
∴AF=BD.
∴AF=DC.
(2)四边形ADCF是菱形,证明如下:
∵AF∥BC,AF=DC,
∴四边形ADCF是平行四边形.
∵AC⊥AB,AD是斜边BC的中线,
∴AD=DC.
∴平行四边形ADCF是菱形.
23.(1)见解析
(2);证明见解析
【分析】(1)先利用已知条件证明,得出,推出,再由即可证明;
(2)延长BC到点M,使CM=CB,连接EM,AM,先证,推出,通过等量代换得到,利用平行线的性质得出,利用直角三角形斜边中线等于斜边一半即可得到.
【详解】(1)证明:在和中,
,
∴ ,
∴ ,
∴ ,
∵,
∴.
(2)解:补全后的图形如图所示,,证明如下:
延长BC到点M,使CM=CB,连接EM,AM,
∵,CM=CB,
∴ 垂直平分BM,
∴,
在和中,
,
∴ ,
∴ ,,
∵,
∴ ,
∴ ,
∵,
∴,
∴ ,即,
∵,
∴ ,
∴ .
【点睛】本题考查全等三角形的判定与性质,垂直平分线的性质,平行线的判定与性质,勾股定理的逆用,直角三角形斜边中线的性质等,第二问有一定难度,正确作辅助线,证明是解题的关键.
24.(1)
(2)
(3)
【分析】(1)首先由折叠的性质可得,再由等腰三角形的性质可求解;
(2)首先由折叠的性质可得,,再由等腰三角形的性质可得,,最后根据角度关系即可求解;
(3)首先由等腰直角三角形的性质和直角三角形的性质可求的长,由勾股定理可求的长,最后根据面积和差关系可求解.
【详解】(1),,,
,
将沿折叠得到,
,
,
∴△ABE是等边三角形,
,
故答案为:60;
(2),理由如下:
将沿折叠得到,
,,
,,
,
,
,
;
(3)如图,连接,
,点是的中点,
,
,,
,,
,
,
,
,
.
【点睛】本题考查了等腰直角三角形的性质,直角三角形的性质,折叠的性质等知识,解题的关键是熟练掌握相关性质并能够灵活运用.
答案第1页,共2页
答案第1页,共2页
