专题18.48矩形、菱形、正方形分类专题 折叠问题 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题18.48矩形、菱形、正方形分类专题 折叠问题 基础篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-27 22:35:05 | ||
图片预览


文档简介
专题18.48 矩形、菱形、正方形分类专题(折叠问题)
(基础篇)(专项练习)
一、单选题
【类型一】矩形的折叠问题
1.如图,折叠长方形纸片ABCD的一边AD,使点D落在边BC上的点F处,AE为折痕,已知AB=6,BC=10,则BF的长为( )
A.6 B.8 C. D.
2.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
3.如图,在矩形纸片中,把沿直线折叠,使得点落在边上的点处.已知与的度数之比为,则的度数是( )
A. B. C. D.
4.如图,矩形沿对角线折叠,已知长,宽,那么折叠后重合部分的面积是( )
A. B. C. D.
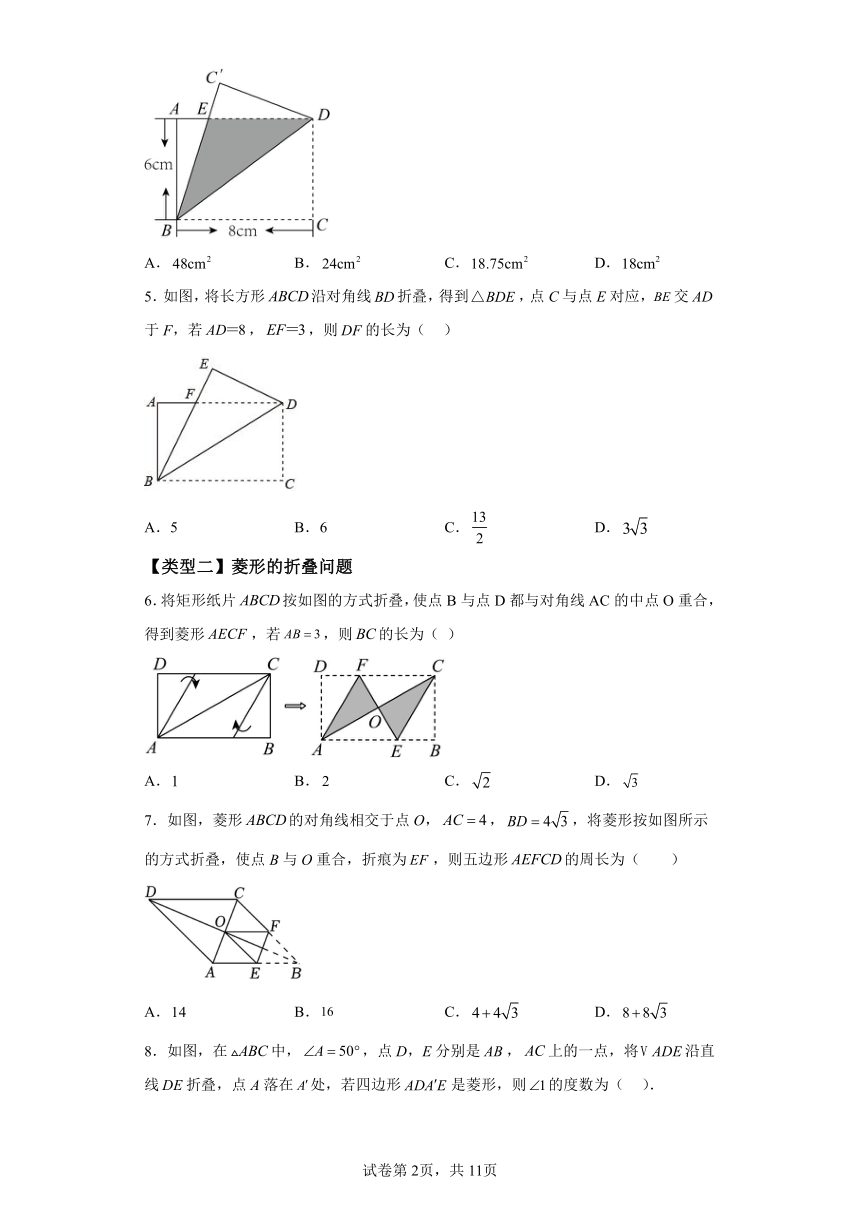
5.如图,将长方形沿对角线折叠,得到,点C与点E对应,交于F,若,,则的长为( )
A.5 B.6 C. D.
【类型二】菱形的折叠问题
6.将矩形纸片按如图的方式折叠,使点B与点D都与对角线AC的中点O重合,得到菱形,若,则的长为( )
A. B. C. D.
7.如图,菱形的对角线相交于点O,,,将菱形按如图所示的方式折叠,使点B与O重合,折痕为,则五边形的周长为( )
A. B. C. D.
8.如图,在中,,点D,E分别是,上的一点,将沿直线折叠,点A落在处,若四边形是菱形,则的度数为( ).
A. B. C. D.
9.如图,把菱形沿折叠,使点落在上的点处,若,则的大小为( ).
A. B. C. D.
10.如图,在中,,将沿折叠,使点落在边上的点处,并且,则的长是( )
A. B. C. D.
【类型三】正方形的折叠问题
11.如图,正方形纸片的边长为5,点和点分别在边与上,将、分别沿,折叠,点、恰好都落在点处,已知,则的长为( )
A. B. C. D.5
12.如图,将正方形纸片按如图折叠, 为折痕,点 落在对角线 上的点 处,则 的度数为( )
A. B. C. D.
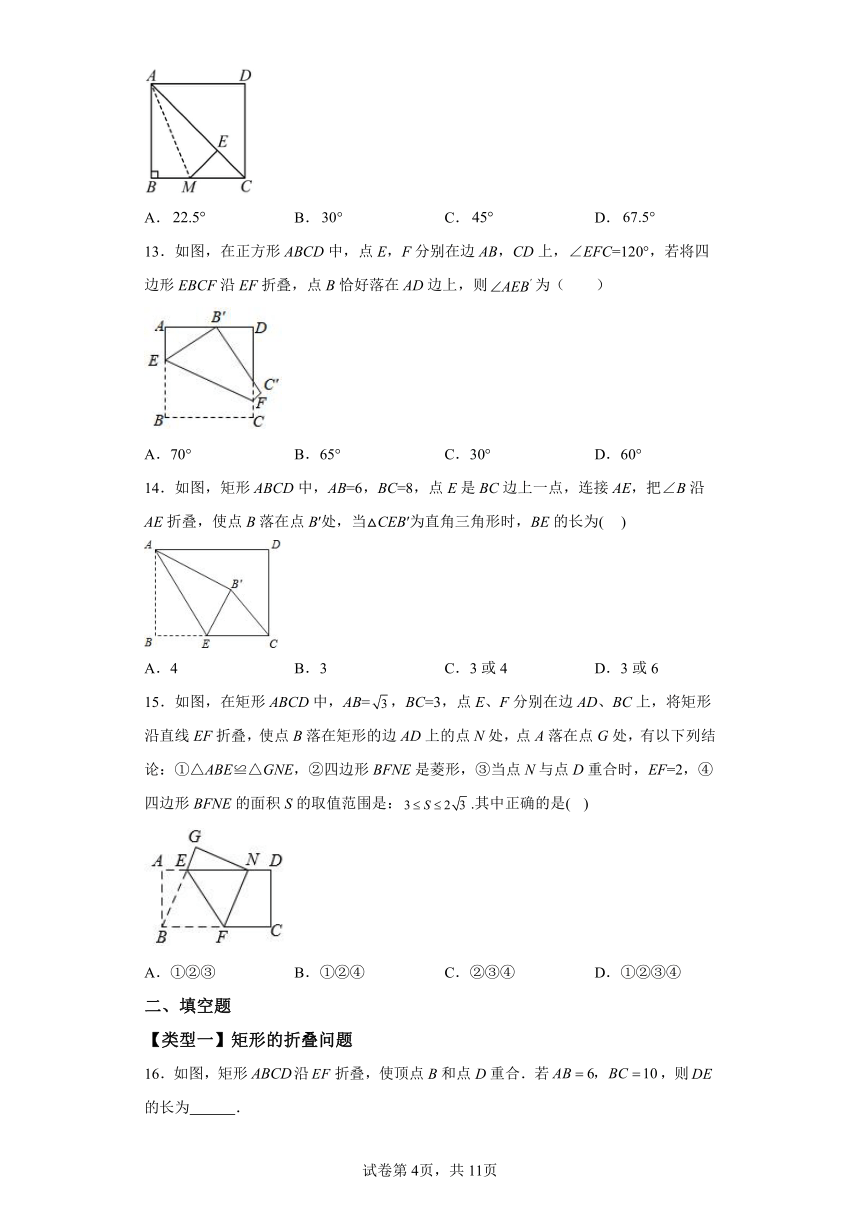
13.如图,在正方形ABCD中,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则为( )
A.70° B.65° C.30° D.60°
14.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A.4 B.3 C.3或4 D.3或6
15.如图,在矩形ABCD中,AB=,BC=3,点E、F分别在边AD、BC上,将矩形沿直线EF折叠,使点B落在矩形的边AD上的点N处,点A落在点G处,有以下列结论:①△ABE≌△GNE,②四边形BFNE是菱形,③当点N与点D重合时,EF=2,④四边形BFNE的面积S的取值范围是:.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
【类型一】矩形的折叠问题
16.如图,矩形沿折叠,使顶点B和点D重合.若,则的长为 .
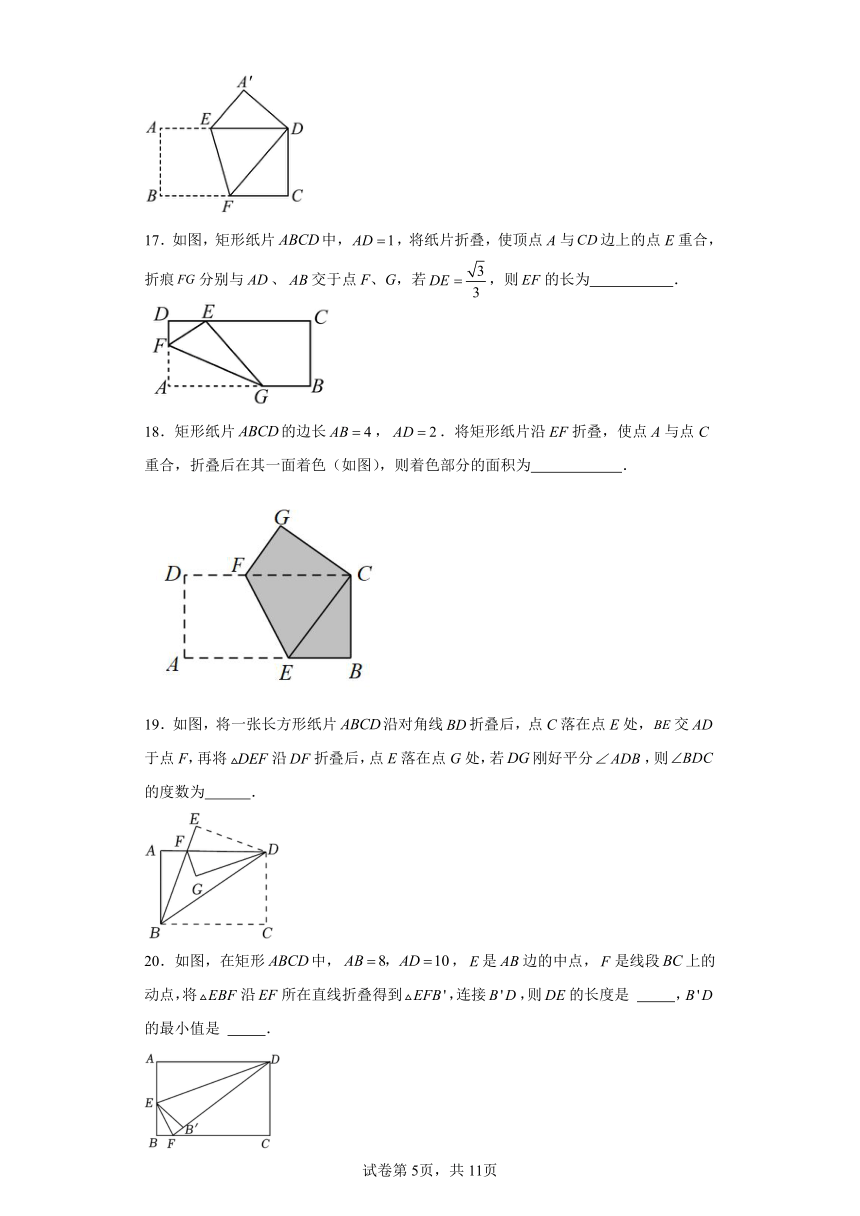
17.如图,矩形纸片中,,将纸片折叠,使顶点A与边上的点E重合,折痕分别与、交于点F、G,若,则的长为 .
18.矩形纸片的边长,.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为 .
19.如图,将一张长方形纸片沿对角线折叠后,点C落在点E处,交于点F,再将沿折叠后,点E落在点G处,若刚好平分,则的度数为 .
20.如图,在矩形中,,是边的中点,是线段上的动点,将沿所在直线折叠得到,连接,则的长度是 ,的最小值是 .
【类型二】菱形的折叠问题
21.如图,在菱形中,,,分别在边,上,,将沿折叠,点落在的延长线上的点处,则的度数为 .
22.如图,在 ABCD中,点E是BC边上的动点,已知AB=4,BC=6,∠B=60°,现将△ABE沿AE折叠,点B′是点B的对应点,设CE长为x.
(1)如图1,当点B′恰好落在AD边上时,x= ;
(2)如图2,若点B′落在△ADE内(包括边界),则x的取值范围是 .
23.如图,在矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠使点D与点B重合,点C的对应点是点C'.若AB=4,EF=,则AD的长等于 .
24.如图,将菱形ABCD沿AE折叠,点B刚好落在线段BC上的点F处,连接DF,若∠BAF=52°,则∠CDF= .
25.图,把菱形ABCD沿AE折叠,点B落在BC边上的F处,若∠BAE=15°,则∠FDC的大小为 .
【类型三】正方形的折叠问题
26.如图,四边形是正方形,E、F分别在边上,将分别沿折叠后,重合于的位置,且点G恰好在连线上.若正方形边长为12,线段长为10,则的长为 .
27.如图,将边长为1的正方形ABCD的一角折叠,折痕为AE,使AB落在对角线AC上的处,则的长为 .
28.如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若FN=3,则正方形纸片的边长为 .
29.如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为 .
30.如图,在正方形中,E是边的中点,将沿折叠,得到,延长交于G,连接,.(1) ;(2) ;(3)正方形的边长为 .
三、解答题
【类型一】矩形的折叠问题
31.如图,在长方形中,,将矩形纸片沿折叠,使点A落在点E处,设与相交于点F.
(1)判断的形状,并说明理由;
(2)求的长.
32.折叠矩形的一边,使点落在边的点处,若,,求:的长.
33.如图所示,折叠矩形的一边,使点D落在边上的点F处,已知,.
(1)求的长;
(2)求的长.
【类型二】菱形的折叠问题
34.如图,在矩形纸片中,,,是边上一点,折叠纸片使点与点重合,其中为折痕,连结、.若,求的长.
35.如图,四边形ABCD是矩形,E、F分别是线段AD、BC上的点,点O是EF与BD的交点.若将△BED沿直线BD折叠,则点E与点F重合.
(1)求证:四边形BEDF是菱形:
(2)若,,求四边形BEDF的面积.
36.矩形ABCD中,AB=9,AD=3,M、N分别是AB、CD上的点,将四边形MBCN沿MN折叠时,点B恰好落在D处,点C落在点E处,连接BN.
(1)求证:四边形DMBN是菱形;
(2)求线段AM之长;
(3)求折痕MN之长.
【类型三】正方形的折叠问题
37.【问题原型】如图①,在中,是边的中线,.
求证:.
【结论应用】如图②,在中,为锐角,为中点,连结,将四边形沿折叠,得到四边形,点、的对应点分别为点、.
(1)与的位置关系是________;
(2)连结,若,求的度数;
(3)如图③,当为边长为4的正方形时,其余条件不变,延长交于点,连结,直接写出线段的长.
38.如图,E、F分别是正方形ABCD边AB、AD的中点,将△ABF沿BF折叠,点A落在点Q处,连接FQ并延长,交DC于G点.
(1)求证:CE=BF;
(2)若AB=4,求GF的值.
39.如图,将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据折叠的性质,AF=AD=10,在Rt△ABF中,利用勾股定理即可求出BF.
【详解】解:根据题意,AF=AD=10,
∴,
故选 B
【点睛】本题考查了翻折变换的性质及勾股定理的应用,解题的关键理解是折叠前后的对应的线段相等.
2.B
【分析】先利用互余计算出,再根据平行线的性质得,接着根据折叠的性质得,于是得到结论.
【详解】解:∵四边形为矩形,
∴,,
又∵,
∴,
∴,
∵矩形沿对角线折叠,
∴.
故选:B.
【点睛】本题考查图形的变换—折叠,考查了矩形的性质,折叠的性质,平行线的性质等知识.理解和掌握折叠的性质是解题的关键.
3.C
【分析】根据矩形的性质得到,由折叠得,设,则,得到,求出,即可求出的度数.
【详解】解:∵四边形是矩形,
∴,
由折叠得,
设,则,
∵,
∴,
∴,
∴,
∴,
故选:C.
【点睛】此题考查了矩形与折叠,熟记矩形的性质是解题的关键.
4.C
【分析】由矩形的性质易得,那么可用表示出,利用的三边关系即可求得长,然后三角形面积公式求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∵
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质,解决此类问题,应利用折叠找到相应的直角三角形,利用勾股定理求得所需线段长度.
5.A
【分析】由翻折的性质可知,由矩形的性质可知,从而得到,于是,故此,证出,则可得出答案.
【详解】解:∵四边形是矩形,
∴.
∴.
由翻折的性质可知:,
∴.
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查了翻折的性质、等腰三角形的性质和判定、矩形的性质,由翻折的性质找出相等的角或边是解题的关键.
6.D
【详解】解:∵折叠
∴∠DAF=∠FAC,AD=AO,BE=EO,
∵AECF是菱形
∴∠FAC=∠CAB,AOE=90°
∴∠DAF=∠FAC=∠CAB
∵DABC是矩形
∴∠DAB=90°,AD=BC
∴∠DAF+∠FAC+∠CAB=90°
∴∠DAF=∠FAC=∠CAB=30°
∴AE=2OE=2BE
∵AB=AE+BE=3
∴AE=2,BE=1
∴在Rt△AEO中,AO==AD
∴BC=
故选D.
7.A
【分析】根据菱形的性质、勾股定理求得,即可得是等边三角形,,根据等边三角形的性质和折叠的性质得和是等边三角形,即可得,,根据,得是的中位线,可得,即可得
【详解】解:∵四边形是菱形,
∴,,,
∴,
∴,
∴是等边三角形,
∴,
∴,
∵折叠,
∴,,
∴,,
∴,,
∴,
,
∴和是等边三角形,
∴,,
∵,,
∴是的中位线,
∴,
∴五边形AEFCD的周长:,
故选:A.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,勾股定理,三角形的中位线,解题的关键是掌握这些知识点,正确计算.
8.B
【分析】由折叠的性质,可得,由菱形的性质可得,由等腰三角形的性质即可求解.
【详解】解:将沿直线折叠,点A落在处,
,
四边形是菱形,
,
.
故选:B.
【点睛】本题主要考查了折叠的性质、菱形的性质和等腰三角形的性质,解题的关键是利用灵活应用相关性质解题.
9.A
【分析】根据菱形的性质,已知菱形的对角相等,故推出,从而得出.又因为,故,,易得解.
【详解】解:根据菱形的对角相等得.
,
.
根据折叠得.
,
,
.
.
故选:A.
【点睛】此题要熟练运用菱形的性质得到有关角和边之间的关系.在计算的过程中,综合运用了等边对等角、三角形的内角和定理以及平行线的性质.注意:折叠的过程中,重合的边和重合的角相等.
10.A
【分析】先判定四边形是菱形,再根据菱形的性质计算.
【详解】解:设,
根据C′D∥BC,
∴∠C′DE=∠DEC=∠DEC′,
∴EC′=DC′,
∵EC=EC′,
∴C′D=EC,
可得四边形是菱形;
即中,
,
,
;
故可得;
解得.
故选:A.
【点睛】本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.
11.C
【分析】由图形折叠可得,因为正方形的边长为5,,求出,在中,运用勾股定理求出,再求出.
【详解】解:由图形折叠可得,
∵正方形的边长为5,,
∴,
在中,
∴,
∴,
解得,
∴.
故选:C.
【点睛】本题主要考查了折叠问题,勾股定理,解题的关键是找准不变的线段,利用勾股定理求解线段.
12.C
【分析】根据正方形的性质可得,,再由折叠可得,然后利用三角形的外角进行计算即可解答.
【详解】解:∵四边形ABCD是正方形,
∴,,
由折叠得:
,
∴,
故选:C.
【点睛】本题考查了正方形的性质,折叠的性质,三角形外角的性质,熟练掌握正方形的性质是解题的关键.
13.D
【分析】依据正方形的性质以及折叠的性质,即可得到=60°.
【详解】解:∵四边形ABCD是正方形,
∴ABCD,∠A=90°,
∴∠BEF+∠EFC=180°,
∵∠EFC=120°,
∴∠BEF=180°-∠EFC=60°,
∵将四边形EBCF沿EF折叠,点B恰好落在AD边上,
∴∠BEF==60°,
∴=180°-∠BEF-=60°,
故选:D.
【点睛】本题考查了正方形的性质,折叠的性质等知识点,能综合性运用性质进行推理是解此题的关键.
14.D
【分析】当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图所示,连接AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8-x,然后在Rt△CEB′中运用勾股定理可计算出x;
②当点B′落在AD边上时,如图所示,此时四边形ABEB′为正方形.
【详解】解:当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图所示,连接AC,
在Rt△ABC中,AB=6,BC=8,
∴AC==10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,
即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=6,
∴CB′=10-6=4,
设BE=x,则EB′=x,CE=8-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴BE=3;
②当点B′落在AD边上时,如图所示,
此时四边形ABEB′为正方形,
∴BE=AB=6,
综上所述,BE的长为3或6,
故选:D.
【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理,注意本题有两种情况,需要分类讨论,避免漏解.
15.D
【分析】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN,可以证明Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN,所以得到∠NEF=∠BFE,可以证EN=BF,又因为EN∥BF,所以四边形EBFN为平行四边形;又因为BF=NF,即可证明四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:可得AB=CD= ,BC=3,在Rt BCN中,由勾股定理可得BN ,求出NO=NC=,证明Rt NOF Rt NCF(HL),得到FC=FO,在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得 ,解得:FC=FO=1,所以EF=2FO=2,故③正确;
④当N和D重合时,菱形BFNE面积最大,S最大= ;当N和A重合时,菱形BFNE面积最小,S最小= ,可以四边形BFNE的面积S的取值范围得④正确;
【详解】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN
在Rt△ABE和Rt△GNE中,
,
∴Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN
∵EN∥BF
∴∠NEF=∠BFE,
又因为∠BFE=∠NFE,
∴∠NEF=∠NFE
∴EN=FN,
∴EN=BF
又因为EN∥BF
∴四边形EBFN为平行四边形;
又因为BF=NF
∴四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:
AB=CD= ,BC=3,
在Rt BCN中,由勾股定理
BN= ,
,
∴N0=NC= ,
在Rt NOF和Rt NCF中,
∴Rt NOF Rt NCF(HL),
∴FC=FO
在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得,
∴
解得:x=1
∴FC=FO=1,
∴EF=2FO=2,故③正确;
当N和D重合时,
菱形BFNE面积最大,S最大= ;
当N和A重合时,
菱形BFNE面积最小,S最小= ,
四边形BFNE的面积S的取值范围是:
故④正确;
故正确的序号是:①②③④;
故选:D
【点睛】本题考查了矩形折叠问题,此题是四边形综合题,主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用,熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键;
16.
【分析】由矩形的性质可得,,由折叠性质可得,,由勾股定理可求的长.
【详解】解:∵四边形是矩形
∴,,
∵折叠,
∴,,
在中,,
∴,
∴,
故答案为:.
【点睛】本题考查了翻折变换,矩形的性质,利用勾股定理求的长度是本题的关键.
17.
【分析】设的长为x,由折叠的性质得,,在中,由勾股定理即可求得x的值,即可得到的长.
【详解】解:设的长为x,
由折叠的性质得,
在矩形纸片中,,,
∴,
在中,
,
∴,
解得,
即的长为.
故答案为:
【点睛】此题考查了勾股定理在折叠问题中的应用,还考查了矩形的性质,根据勾股定理列方程是解题的关键.
18.####
【分析】根据矩形的性质,可得与的关系,根据翻折的性质,可得;与的关系,根据全等三角形的判定与性质,可得与的关系,根据勾股定理,可得的长,根据面积的和差,可得答案.
【详解】∵是矩形,
∴,
设,则,
在中,
∴,即,解得,
∴,
∴.
故答案为:.
【点睛】本题主要考查了图形的翻折变化,矩形的性质,关键是掌握折叠是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
19.54°##54度
【分析】根据折叠的性质可得,,由角平分线的定义可得,然后根据矩形的定义及角的运算可得答案.
【详解】解:∵四边形是矩形,
∴,
由折叠得:,,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:54°.
【点睛】本题考查了折叠的性质,矩形的性质、角平分线的定义、角的运算.
20.
【分析】根据矩形的性质和勾股定理求出的长,再根据三角形的三边关系进而得出的最小值.
【详解】解:∵四边形是矩形,
∴
∵是边的中点
∴
∴
由折叠得
∵
∴
∴
∴的最小值是
故答案为:,.
【点睛】本题考查了矩形的性质,勾股定理,折叠的性质,三角形的三边关系等相关知识点,理解三角形三边关系是解题的关键.
21.20°##20度
【分析】由菱形的性质得出AB=AD,∠B=∠D=60°,证明△ABG≌△ADE(SAS),由全等三角形的性质得出∠BAG=∠DAE,由折叠的性质得出∠DAE=∠FAE,∠AED=∠AEF,由三角形内角和定理可得出答案.
【详解】解:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D=60°,
∴∠BAD=120°,
在△ABG和△ADE中,
,
∴△ABG≌△ADE(SAS),
∴∠BAG=∠DAE,
∵将△ADE沿AE折叠,
∴∠DAE=∠FAE,∠AED=∠AEF,
∴∠DAE=∠BAD=40°,
∴∠AED=180°-∠DAE-∠D=180°-40°-60°=80°,
∴∠FEC=180°2∠AED=180°160°=20°,
故答案为:20°.
【点睛】本题考查了菱形的性质,折叠的性质,全等三角形的判定与性质,熟练掌握折叠的性质是解题的关键.
22. 2
【分析】(1)根据折叠的性质知EC=BC-BE=6-4=2;
(2)当B'落在DE上时,作AH⊥DE于H,由折叠的性质可证AD=DE,再利用△AB'H是含30°的直角三角形,从而求出DB'的长,即可解决问题.
【详解】(1)∵将△ABE沿AE折叠,点B′是点B的对应点,
∴AB=AB’, ∠B=∠AB'E,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AB∥CD,AD∥BC,
∴∠AB’E=∠ADC,
∴B’E∥CD,
∴B’E∥AB,
∴四边形ABEB’是平行四边形,
∵AB=AB’,
四边形ABEB'是菱形,
∴EC=BC-BE=6-4=2,
故答案为:2;
(2)如图,当B'落在DE上时,作AH⊥DE于H,
在Rt△AHB'中,
∵∠AB'H=60°,AB'=4,
∴HB'=AB′=2,AH=HB′=,
在Rt△ADH中,
,
∵AD∥BC,
∴∠DAE=∠AEB=∠AED,
∴DA=DE=6,
∴,
∴,
∴若点B′落在△ADE内(包括边界),则x的取值范围是,
故答案为:.
【点睛】本题主要考查了平行四边形的性质,翻折变换,含30°角的直角三角形的性质等知识,找到临界状态求出x的长是解题的关键.
23.8
【分析】由折叠得到,结合矩形的性质,解得,继而证明四边形是菱形,由菱形对角线的性质结合菱形的面积解得,最后在中,利用勾股定理解得的长即可.
【详解】解:由折叠的性质可知
连接,与相交于点,
折叠
四边形是菱形,
中,
设
在中,
故答案为:8.
【点睛】本题考查矩形与折叠、菱形的判定与性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
24.6°
【分析】首先根据折叠的性质得出,然后根据菱形的性质求出的度数,最后利用求解即可.
【详解】根据折叠的性质有,
.
∵四边形ABCD是菱形,
,
,
,
,
,
故答案为:6°.
【点睛】本题主要考查菱形的性质和折叠的性质,掌握菱形的性质和折叠的性质是解题的关键.
25.22.5°
【分析】根据翻折变换的性质可得AB=AF,然后根据等腰三角形两底角相等求出∠B=∠AFE=75°,可得∠C,根据AF=AD,求出∠AFD,由三角形外角等于不相邻的两个内角的和即可得答案.
【详解】解:∵菱形ABCD沿AE折叠,B落在BC边上的点F处,
∴AD=AB=AF,∠AEB=90°=∠AEF,∠FAE=∠BAE=15°,
∴∠B=∠AFE=75°,
在菱形ABCD中,AB∥CD,AD∥BC,
∴∠DAF=∠AFE=75°,∠C=180°-∠B=105°,
∵AF=AD,
∴∠ADF=∠AFD==52.5°,
∴∠DFB=∠AFE+∠AFD=127.5°,
∴∠FDC=∠DFB-∠B=22.5°,
故答案为:22.5°.
【点睛】本题考查了菱形中的翻折问题,等腰三角形的性质,解题的关键是掌握翻折的性质及菱形的性质.
26.6或8##8或6
【分析】由折叠的性质可得,再根据已知条件推出,设,则,在中,由勾股定理得:,即,据此求解即可.
【详解】解:由折叠的性质可得,
∵,
∴,
∵四边形是正方形且边长为12,
∴,
∴,
∴,
设,则,
在中,由勾股定理得:,
∴,
解得或,
∴的长为6或8,
故答案为:6或8.
【点睛】本题主要考查了折叠的性质,正方形的性质,勾股定理,推出是解题的关键.
27.##
【分析】根据正方形的性质与折叠的性质可得,设,则,勾股定理即可求解.
【详解】解:∵四边形是正方形,
∴,,
,
是等腰直角三角形,
设,则,,
在中,,
,
解得,
故答案为:.
【点睛】本题考查了正方形的折叠问题,掌握正方形的性质与折叠的性质是解题的关键.
28.
【分析】设正方形的边长为a,根据折叠得出,,根据勾股定理列出关于a的方程,解方程即可.
【详解】解:设正方形的边长为a,则根据折叠可知,,,
在Rt△BFN中,根据勾股定理可知,,
即:,
解得:或(舍去).
故答案为:.
【点睛】本题主要考查了正方形的折叠问题,勾股定理的应用,设出正方形的边长,根据勾股定理列出关于a的方程,是解题的关键.
29.
【分析】设DF=EF=x,分别表示出DA=DC= 、AC= ,利用勾股定理列方程解得,利用等积法求出结果.
【详解】解:由折叠知AF平分∠DAE,∠D=90°,FE⊥AC于于点F,
∴FD=FE,
设DF=EF=x,
在直角△EFC中,∠FCE=45°,
∴EC=EF=x,
∴FC= ,
∴DA=DC= ,
∴AC= ,
在直角△ADF中,
∴AD2+DF2=AF2,
即 ,
解得 ,
又∵ ,
∴,
故答案为 .
【点睛】本题考查正方形的性质、勾股定理以及等积法的应用,解决问题的关键是利用三角形的面积有两种不同的表示方法确定等量关系.
30. 1 45 3
【分析】(1)由翻折的性质及全等三角形的性质可求出AG=FG;
(2)根据正方形的性质及角的和差关系可得;
(3)设边长为x,得到BG=x-1,BE=,GE=1+,根据勾股定理列出方程,故可求解.
【详解】(1)根据折叠的意义,得△DEC≌△DEF,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,
∴Rt△ADG≌Rt△FDG(HL),
∴∠ADG=∠FDG,AG=FG=1
(2)∵△DEC≌△DEF,Rt△ADG≌Rt△FDG
∴∠GDE=∠FDG+∠FDE=(∠ADF+∠CDF)=45°
(3)∵△DEC≌△DEF,Rt△ADG≌Rt△FDG
∴GF=GA=1,EC=EF
设正方形边长为x,得到BG=x-1,BE=,GE=1+,
在Rt△BEG中,GE2=BG2+BE2
∴(1+)2=(x-1)2+()2
解得x=3
∴正方形的边长为3
故答案为:1;45;3.
【点睛】此题考查了翻折性质、正方形的性质、全等三角形的判定与性质等,掌握其性质是解决此题关键.
31.(1)是直角三角形,理由见解析
(2)
【分析】(1)利用翻折变换的性质及矩形的性质即可求解;
(2)利用翻折变换的性质即可求解.
【详解】(1)是直角三角形,
∵四边形是矩形,
∴,
∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴是直角三角形;
(2)∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴四边形是矩形,,
∴,
∴.
【点睛】本题考查了折叠的性质,矩形的性质,掌握折叠的性质是解题的关键.
32.
【分析】根据勾股定理求出的长;进而求出的长度;由题意得;利用勾股定理列出关于的方程,解方程即可解决问题.
【详解】解:四边形为矩形,
,,;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
【点睛】本题主要考查了翻折变换的性质及其应用问题,解题的关键是掌握折叠的性质,熟练运用勾股定理列方程解决问题.
33.(1);
(2).
【分析】(1)由折叠的性质可得:,利用勾股定理求解即可;
(2)由(1)可得,设,则利用勾股定理求解即可.
【详解】(1)解:由矩形的性质可得:,,
由折叠的性质可得:,
由勾股定理可得:;
(2)解:由(1)可得,
设,则,
在中,,即
解得,即.
【点睛】此题考查了矩形的折叠问题,涉及了勾股定理,解题的关键是能够利用勾股定理灵活求解.
34..
【分析】利用对称的性质得出,进而得出,证明四边形是菱形,再利用菱形的性质结合勾股定理得出答案.
【详解】解:∵B、E两点关于直线对称,
∴,
在矩形中,,
∴,
∴,
∴,
∴,
∴四边形是菱形;
设菱形的边长为x,
∴,
在中,,
∴,
∴解得:.
∴.
【点睛】此题主要考查了菱形的判定与性质以及勾股定理,正确应用轴对称的性质是解题关键.
35.(1)见解析
(2)菱形BEDF的面积为.
【分析】(1)证明△OBF≌△ODE,得到OB=OD即可得出结论;
(2)由ED=2AE,由AB AD=,求得S△ABD=AB AD=,再由ED=2AE,可求得S△BDE=,进而可得出菱形BEDF的面积.
【详解】(1)证明:将△BED沿BD折叠,使E,F重合,
∴OE=OF,EF⊥BD,
∵四边形ABCD是矩形,
∴∠C=90°,AD∥BC,
∴∠ODE=∠OBF,
在△OBF和△ODE中,
,
∴△OBF≌△ODE(AAS),
∴OB=OD,
∵OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形;
(2)解:∵AB AD=,
∴S△ABD=AB AD=,
∵ED=2AE,
∴ED=AD,
∴S△BDE:S△ABD=2:3,
∴S△BDE=,
∴菱形BEDF的面积=2S△BDE=.
【点睛】本题考查了翻折变换的性质、菱形的判定与性质、矩形的性质等知识;熟练掌握菱形的判定与性质是解题的关键.
36.(1)见解析
(2)4
(3)
【分析】(1)根据折叠的性质可得BM=DM,DN=BN,∠DMN=∠BMN,再由四边形ABCD是矩形,可得AB∥CD,从而得到∠DNM=∠BMN,进而得到∠DNM=∠DMN,继而得到DM=DN,即可求证;
(2)设AM=x,则DM=BM=AB-AM=9-x,在中,由勾股定理,即可求解;
(3)连接BD,由勾股定理可得,再根据,即可求解.
【详解】(1)证明:根据题意得:BM=DM,DN=BN,∠DMN=∠BMN,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DNM=∠BMN,
∴∠DNM=∠DMN,
∴DM=DN,
∴DM=BM=DN=BN,
∴四边形DMBN是菱形;
(2)解:设AM=x,则DM=BM=AB-AM=9-x,
∵四边形ABCD是矩形,
∴∠A=90°,
在中,,
∴,解得:x=4,
即AM=4;
(3)解:如图,连接BD,
∵四边形ABCD是矩形,
∴∠A=90°,
在中, AB=9,AD=3,
∴,
由(2)得:AM=4,
∴BM=5,
∵,
∴,
解得:.
【点睛】本题主要考查了矩形的性质,菱形的判定和性质,勾股定理,折叠的性质,熟练掌握矩形的性质,菱形的判定和性质,勾股定理,折叠的性质是解题的关键.
37.[问题原型] 见解析;
[结论应用](1);(2)(3)
【分析】[问题原型] 由等腰三角形的性质可得,,由三角形内角和定理可得结论;
[结论应用]
(1)根据轴对称的性质得出;
(2)根据平行线的性质即可求解;
(3)证明,设,在中,勾股定理列出方程,解方程即可求解.
【详解】[问题原型]证明:是边的中线,.
,
,,
,
,
;
[结论应用](1)依题意点、的对应点分别为点、
∴关于对称,
∴,
(2)∵为中点,
由[问题原型]可得
又,
∴,
∵,
∴;
(3)∵四边形是正方形,
∴,
∵折叠,
∴,,
∴,
∵为中点,
∴,
∴,
在与中,
∴,
设,
在中,,
,,
∵,
∴,
解得,
即.
【点睛】本题考查了折叠的性质,等腰三角形的性质与判定,平行线的性质,平行四边形的性质,正方形的性质,勾股定理,掌握折叠的的性质是解题的关键.
38.(1)见解析
(2)GF的值为.
【分析】(1)先判断出AF=BE,进而得出△FAB≌△EBC(SAS),即可得出结论;
(2)连接BG,根据HL证明Rt△BQG≌Rt△BCG,得QG=GC,设QG=b,在Rt△DFG中,根据勾股定理列方程可得b,从而可得结论.
【详解】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠A=∠ABC=90°,
∵E、F分别是正方形ABCD边AB、AD的中点,
∵AF=BE,
∴△FAB≌△EBC(SAS),
∴CE=BF;
(2)解:如图,连接BG,
由折叠得:AB=BQ,∠BQF=∠A=90°,
∵AB=BC,
∴BC=BQ,
∵BG=BG,
∴Rt△BQG≌Rt△BCG(HL),
∴QG=GC,
∵AB=4,F是正方形ABCD边AD的中点,
设QG=b,
则DF=AF=FQ=2,FG=2+b,DG=4-b,
在Rt△DFG中,∵DF2+DG2=FG2,
∴,
∴b=,即QG=,
∴GF=FQ+QG=2+=.
∴GF的值为.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,正确作辅助线是本题的关键.
39.(1)CN=3;(2)正方形的面积为80
【分析】(1)根据题意易得DN=NE,BE=EC=4,设CN=x,则有DN=8-x,然后根据勾股定理进行求解即可;
(2)过点M作MG⊥CD于点G,连接DE,证明△MNG≌△DEC,则有MN=DE,进而根据勾股定理及正方形的面积公式可求解.
【详解】解:(1)∵将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,
∴DN=NE,BE=EC=4,
设CN=x,则有DN=8-x,
∴在Rt△ECN中,,即,
解得,即CN=3;
(2)过点M作MG⊥CD于点G,连接DE,交MN于点H,如图所示:
由题意可得AM=DG,MG=BC=CD,∠MGN=∠C=90°,
根据折叠的性质可得:DE⊥MN,
∴∠NMG+∠MHE=90°,
∵∠EDC+∠DHG=90°,∠DHG=∠MHE,
∴∠NMG=∠EDC,
∴△MNG≌△DEC(ASA),
∴MN=DE,
在Rt△DEC中,,
∴,
∴以MN为边的正方形面积为:.
【点睛】本题主要考查正方形的性质、折叠的性质、全等三角形的性质与判定及勾股定理,熟练掌握正方形的性质、折叠的性质、全等三角形的性质与判定及勾股定理是解题的关键.
答案第1页,共2页
答案第1页,共2页
(基础篇)(专项练习)
一、单选题
【类型一】矩形的折叠问题
1.如图,折叠长方形纸片ABCD的一边AD,使点D落在边BC上的点F处,AE为折痕,已知AB=6,BC=10,则BF的长为( )
A.6 B.8 C. D.
2.如图,将矩形沿对角线折叠,使点落在处,交于点.若,则的度数为( )
A. B. C. D.
3.如图,在矩形纸片中,把沿直线折叠,使得点落在边上的点处.已知与的度数之比为,则的度数是( )
A. B. C. D.
4.如图,矩形沿对角线折叠,已知长,宽,那么折叠后重合部分的面积是( )
A. B. C. D.
5.如图,将长方形沿对角线折叠,得到,点C与点E对应,交于F,若,,则的长为( )
A.5 B.6 C. D.
【类型二】菱形的折叠问题
6.将矩形纸片按如图的方式折叠,使点B与点D都与对角线AC的中点O重合,得到菱形,若,则的长为( )
A. B. C. D.
7.如图,菱形的对角线相交于点O,,,将菱形按如图所示的方式折叠,使点B与O重合,折痕为,则五边形的周长为( )
A. B. C. D.
8.如图,在中,,点D,E分别是,上的一点,将沿直线折叠,点A落在处,若四边形是菱形,则的度数为( ).
A. B. C. D.
9.如图,把菱形沿折叠,使点落在上的点处,若,则的大小为( ).
A. B. C. D.
10.如图,在中,,将沿折叠,使点落在边上的点处,并且,则的长是( )
A. B. C. D.
【类型三】正方形的折叠问题
11.如图,正方形纸片的边长为5,点和点分别在边与上,将、分别沿,折叠,点、恰好都落在点处,已知,则的长为( )
A. B. C. D.5
12.如图,将正方形纸片按如图折叠, 为折痕,点 落在对角线 上的点 处,则 的度数为( )
A. B. C. D.
13.如图,在正方形ABCD中,点E,F分别在边AB,CD上,∠EFC=120°,若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则为( )
A.70° B.65° C.30° D.60°
14.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为( )
A.4 B.3 C.3或4 D.3或6
15.如图,在矩形ABCD中,AB=,BC=3,点E、F分别在边AD、BC上,将矩形沿直线EF折叠,使点B落在矩形的边AD上的点N处,点A落在点G处,有以下列结论:①△ABE≌△GNE,②四边形BFNE是菱形,③当点N与点D重合时,EF=2,④四边形BFNE的面积S的取值范围是:.其中正确的是( )
A.①②③ B.①②④ C.②③④ D.①②③④
二、填空题
【类型一】矩形的折叠问题
16.如图,矩形沿折叠,使顶点B和点D重合.若,则的长为 .
17.如图,矩形纸片中,,将纸片折叠,使顶点A与边上的点E重合,折痕分别与、交于点F、G,若,则的长为 .
18.矩形纸片的边长,.将矩形纸片沿EF折叠,使点A与点C重合,折叠后在其一面着色(如图),则着色部分的面积为 .
19.如图,将一张长方形纸片沿对角线折叠后,点C落在点E处,交于点F,再将沿折叠后,点E落在点G处,若刚好平分,则的度数为 .
20.如图,在矩形中,,是边的中点,是线段上的动点,将沿所在直线折叠得到,连接,则的长度是 ,的最小值是 .
【类型二】菱形的折叠问题
21.如图,在菱形中,,,分别在边,上,,将沿折叠,点落在的延长线上的点处,则的度数为 .
22.如图,在 ABCD中,点E是BC边上的动点,已知AB=4,BC=6,∠B=60°,现将△ABE沿AE折叠,点B′是点B的对应点,设CE长为x.
(1)如图1,当点B′恰好落在AD边上时,x= ;
(2)如图2,若点B′落在△ADE内(包括边界),则x的取值范围是 .
23.如图,在矩形ABCD中,点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠使点D与点B重合,点C的对应点是点C'.若AB=4,EF=,则AD的长等于 .
24.如图,将菱形ABCD沿AE折叠,点B刚好落在线段BC上的点F处,连接DF,若∠BAF=52°,则∠CDF= .
25.图,把菱形ABCD沿AE折叠,点B落在BC边上的F处,若∠BAE=15°,则∠FDC的大小为 .
【类型三】正方形的折叠问题
26.如图,四边形是正方形,E、F分别在边上,将分别沿折叠后,重合于的位置,且点G恰好在连线上.若正方形边长为12,线段长为10,则的长为 .
27.如图,将边长为1的正方形ABCD的一角折叠,折痕为AE,使AB落在对角线AC上的处,则的长为 .
28.如图,把正方形纸片ABCD沿对边中点所在的直线对折后展开,折痕为MN,再过点B折叠纸片,使点A落在MN上的点F处,折痕为BE.若FN=3,则正方形纸片的边长为 .
29.如图,沿对角线AC折叠正方形ABCD,使得B、D重合,再折叠,点D恰好落在AC上的点E处,测得折痕AF的长为3,则C到AF的距离CG为 .
30.如图,在正方形中,E是边的中点,将沿折叠,得到,延长交于G,连接,.(1) ;(2) ;(3)正方形的边长为 .
三、解答题
【类型一】矩形的折叠问题
31.如图,在长方形中,,将矩形纸片沿折叠,使点A落在点E处,设与相交于点F.
(1)判断的形状,并说明理由;
(2)求的长.
32.折叠矩形的一边,使点落在边的点处,若,,求:的长.
33.如图所示,折叠矩形的一边,使点D落在边上的点F处,已知,.
(1)求的长;
(2)求的长.
【类型二】菱形的折叠问题
34.如图,在矩形纸片中,,,是边上一点,折叠纸片使点与点重合,其中为折痕,连结、.若,求的长.
35.如图,四边形ABCD是矩形,E、F分别是线段AD、BC上的点,点O是EF与BD的交点.若将△BED沿直线BD折叠,则点E与点F重合.
(1)求证:四边形BEDF是菱形:
(2)若,,求四边形BEDF的面积.
36.矩形ABCD中,AB=9,AD=3,M、N分别是AB、CD上的点,将四边形MBCN沿MN折叠时,点B恰好落在D处,点C落在点E处,连接BN.
(1)求证:四边形DMBN是菱形;
(2)求线段AM之长;
(3)求折痕MN之长.
【类型三】正方形的折叠问题
37.【问题原型】如图①,在中,是边的中线,.
求证:.
【结论应用】如图②,在中,为锐角,为中点,连结,将四边形沿折叠,得到四边形,点、的对应点分别为点、.
(1)与的位置关系是________;
(2)连结,若,求的度数;
(3)如图③,当为边长为4的正方形时,其余条件不变,延长交于点,连结,直接写出线段的长.
38.如图,E、F分别是正方形ABCD边AB、AD的中点,将△ABF沿BF折叠,点A落在点Q处,连接FQ并延长,交DC于G点.
(1)求证:CE=BF;
(2)若AB=4,求GF的值.
39.如图,将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,点A落在F处,折痕为MN.
(1)求线段CN的长;
(2)求以线段MN为边长的正方形的面积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据折叠的性质,AF=AD=10,在Rt△ABF中,利用勾股定理即可求出BF.
【详解】解:根据题意,AF=AD=10,
∴,
故选 B
【点睛】本题考查了翻折变换的性质及勾股定理的应用,解题的关键理解是折叠前后的对应的线段相等.
2.B
【分析】先利用互余计算出,再根据平行线的性质得,接着根据折叠的性质得,于是得到结论.
【详解】解:∵四边形为矩形,
∴,,
又∵,
∴,
∴,
∵矩形沿对角线折叠,
∴.
故选:B.
【点睛】本题考查图形的变换—折叠,考查了矩形的性质,折叠的性质,平行线的性质等知识.理解和掌握折叠的性质是解题的关键.
3.C
【分析】根据矩形的性质得到,由折叠得,设,则,得到,求出,即可求出的度数.
【详解】解:∵四边形是矩形,
∴,
由折叠得,
设,则,
∵,
∴,
∴,
∴,
∴,
故选:C.
【点睛】此题考查了矩形与折叠,熟记矩形的性质是解题的关键.
4.C
【分析】由矩形的性质易得,那么可用表示出,利用的三边关系即可求得长,然后三角形面积公式求解即可.
【详解】解:∵四边形是矩形,
∴,
∴,
∵
∴,
∴,
∴,
∵,
∴,
∴,
∴.
故选:C.
【点睛】本题考查了矩形的性质,折叠的性质,解决此类问题,应利用折叠找到相应的直角三角形,利用勾股定理求得所需线段长度.
5.A
【分析】由翻折的性质可知,由矩形的性质可知,从而得到,于是,故此,证出,则可得出答案.
【详解】解:∵四边形是矩形,
∴.
∴.
由翻折的性质可知:,
∴.
∴,
∵,
∴,
∴,
故选:A.
【点睛】本题考查了翻折的性质、等腰三角形的性质和判定、矩形的性质,由翻折的性质找出相等的角或边是解题的关键.
6.D
【详解】解:∵折叠
∴∠DAF=∠FAC,AD=AO,BE=EO,
∵AECF是菱形
∴∠FAC=∠CAB,AOE=90°
∴∠DAF=∠FAC=∠CAB
∵DABC是矩形
∴∠DAB=90°,AD=BC
∴∠DAF+∠FAC+∠CAB=90°
∴∠DAF=∠FAC=∠CAB=30°
∴AE=2OE=2BE
∵AB=AE+BE=3
∴AE=2,BE=1
∴在Rt△AEO中,AO==AD
∴BC=
故选D.
7.A
【分析】根据菱形的性质、勾股定理求得,即可得是等边三角形,,根据等边三角形的性质和折叠的性质得和是等边三角形,即可得,,根据,得是的中位线,可得,即可得
【详解】解:∵四边形是菱形,
∴,,,
∴,
∴,
∴是等边三角形,
∴,
∴,
∵折叠,
∴,,
∴,,
∴,,
∴,
,
∴和是等边三角形,
∴,,
∵,,
∴是的中位线,
∴,
∴五边形AEFCD的周长:,
故选:A.
【点睛】本题考查了菱形的性质,等边三角形的判定与性质,勾股定理,三角形的中位线,解题的关键是掌握这些知识点,正确计算.
8.B
【分析】由折叠的性质,可得,由菱形的性质可得,由等腰三角形的性质即可求解.
【详解】解:将沿直线折叠,点A落在处,
,
四边形是菱形,
,
.
故选:B.
【点睛】本题主要考查了折叠的性质、菱形的性质和等腰三角形的性质,解题的关键是利用灵活应用相关性质解题.
9.A
【分析】根据菱形的性质,已知菱形的对角相等,故推出,从而得出.又因为,故,,易得解.
【详解】解:根据菱形的对角相等得.
,
.
根据折叠得.
,
,
.
.
故选:A.
【点睛】此题要熟练运用菱形的性质得到有关角和边之间的关系.在计算的过程中,综合运用了等边对等角、三角形的内角和定理以及平行线的性质.注意:折叠的过程中,重合的边和重合的角相等.
10.A
【分析】先判定四边形是菱形,再根据菱形的性质计算.
【详解】解:设,
根据C′D∥BC,
∴∠C′DE=∠DEC=∠DEC′,
∴EC′=DC′,
∵EC=EC′,
∴C′D=EC,
可得四边形是菱形;
即中,
,
,
;
故可得;
解得.
故选:A.
【点睛】本题通过折叠变换考查学生的逻辑思维能力,解决此类问题,应结合题意,最好实际操作图形的折叠,易于找到图形间的关系.
11.C
【分析】由图形折叠可得,因为正方形的边长为5,,求出,在中,运用勾股定理求出,再求出.
【详解】解:由图形折叠可得,
∵正方形的边长为5,,
∴,
在中,
∴,
∴,
解得,
∴.
故选:C.
【点睛】本题主要考查了折叠问题,勾股定理,解题的关键是找准不变的线段,利用勾股定理求解线段.
12.C
【分析】根据正方形的性质可得,,再由折叠可得,然后利用三角形的外角进行计算即可解答.
【详解】解:∵四边形ABCD是正方形,
∴,,
由折叠得:
,
∴,
故选:C.
【点睛】本题考查了正方形的性质,折叠的性质,三角形外角的性质,熟练掌握正方形的性质是解题的关键.
13.D
【分析】依据正方形的性质以及折叠的性质,即可得到=60°.
【详解】解:∵四边形ABCD是正方形,
∴ABCD,∠A=90°,
∴∠BEF+∠EFC=180°,
∵∠EFC=120°,
∴∠BEF=180°-∠EFC=60°,
∵将四边形EBCF沿EF折叠,点B恰好落在AD边上,
∴∠BEF==60°,
∴=180°-∠BEF-=60°,
故选:D.
【点睛】本题考查了正方形的性质,折叠的性质等知识点,能综合性运用性质进行推理是解此题的关键.
14.D
【分析】当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图所示,连接AC,先利用勾股定理计算出AC=10,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=6,可计算出CB′=4,设BE=x,则EB′=x,CE=8-x,然后在Rt△CEB′中运用勾股定理可计算出x;
②当点B′落在AD边上时,如图所示,此时四边形ABEB′为正方形.
【详解】解:当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如图所示,连接AC,
在Rt△ABC中,AB=6,BC=8,
∴AC==10,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,
即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=6,
∴CB′=10-6=4,
设BE=x,则EB′=x,CE=8-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴BE=3;
②当点B′落在AD边上时,如图所示,
此时四边形ABEB′为正方形,
∴BE=AB=6,
综上所述,BE的长为3或6,
故选:D.
【点睛】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等;对应角相等.也考查了矩形的性质以及勾股定理,注意本题有两种情况,需要分类讨论,避免漏解.
15.D
【分析】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN,可以证明Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN,所以得到∠NEF=∠BFE,可以证EN=BF,又因为EN∥BF,所以四边形EBFN为平行四边形;又因为BF=NF,即可证明四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:可得AB=CD= ,BC=3,在Rt BCN中,由勾股定理可得BN ,求出NO=NC=,证明Rt NOF Rt NCF(HL),得到FC=FO,在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得 ,解得:FC=FO=1,所以EF=2FO=2,故③正确;
④当N和D重合时,菱形BFNE面积最大,S最大= ;当N和A重合时,菱形BFNE面积最小,S最小= ,可以四边形BFNE的面积S的取值范围得④正确;
【详解】①由矩形的性质,折叠可知:∠A=∠G=90°AB=GN,BE=EN
在Rt△ABE和Rt△GNE中,
,
∴Rt△ABE≌Rt△GNE(HL),故①正确;
②由矩形的性质,折叠可知:EN∥BF,BF=FN
∵EN∥BF
∴∠NEF=∠BFE,
又因为∠BFE=∠NFE,
∴∠NEF=∠NFE
∴EN=FN,
∴EN=BF
又因为EN∥BF
∴四边形EBFN为平行四边形;
又因为BF=NF
∴四边形EBFN为菱形;故②正确;
③当点N与点D重合时,如图所示:
AB=CD= ,BC=3,
在Rt BCN中,由勾股定理
BN= ,
,
∴N0=NC= ,
在Rt NOF和Rt NCF中,
∴Rt NOF Rt NCF(HL),
∴FC=FO
在Rt NFC中,设FC=x,则NF=3-x,由勾股定理可得,
∴
解得:x=1
∴FC=FO=1,
∴EF=2FO=2,故③正确;
当N和D重合时,
菱形BFNE面积最大,S最大= ;
当N和A重合时,
菱形BFNE面积最小,S最小= ,
四边形BFNE的面积S的取值范围是:
故④正确;
故正确的序号是:①②③④;
故选:D
【点睛】本题考查了矩形折叠问题,此题是四边形综合题,主要考查了折叠问题与菱形的判定与性质、勾股定理的综合应用,熟练掌握菱形的判定定理和性质定理、勾股定理是解本题的关键;
16.
【分析】由矩形的性质可得,,由折叠性质可得,,由勾股定理可求的长.
【详解】解:∵四边形是矩形
∴,,
∵折叠,
∴,,
在中,,
∴,
∴,
故答案为:.
【点睛】本题考查了翻折变换,矩形的性质,利用勾股定理求的长度是本题的关键.
17.
【分析】设的长为x,由折叠的性质得,,在中,由勾股定理即可求得x的值,即可得到的长.
【详解】解:设的长为x,
由折叠的性质得,
在矩形纸片中,,,
∴,
在中,
,
∴,
解得,
即的长为.
故答案为:
【点睛】此题考查了勾股定理在折叠问题中的应用,还考查了矩形的性质,根据勾股定理列方程是解题的关键.
18.####
【分析】根据矩形的性质,可得与的关系,根据翻折的性质,可得;与的关系,根据全等三角形的判定与性质,可得与的关系,根据勾股定理,可得的长,根据面积的和差,可得答案.
【详解】∵是矩形,
∴,
设,则,
在中,
∴,即,解得,
∴,
∴.
故答案为:.
【点睛】本题主要考查了图形的翻折变化,矩形的性质,关键是掌握折叠是一种对称变换,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
19.54°##54度
【分析】根据折叠的性质可得,,由角平分线的定义可得,然后根据矩形的定义及角的运算可得答案.
【详解】解:∵四边形是矩形,
∴,
由折叠得:,,
∵平分,
∴,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
故答案为:54°.
【点睛】本题考查了折叠的性质,矩形的性质、角平分线的定义、角的运算.
20.
【分析】根据矩形的性质和勾股定理求出的长,再根据三角形的三边关系进而得出的最小值.
【详解】解:∵四边形是矩形,
∴
∵是边的中点
∴
∴
由折叠得
∵
∴
∴
∴的最小值是
故答案为:,.
【点睛】本题考查了矩形的性质,勾股定理,折叠的性质,三角形的三边关系等相关知识点,理解三角形三边关系是解题的关键.
21.20°##20度
【分析】由菱形的性质得出AB=AD,∠B=∠D=60°,证明△ABG≌△ADE(SAS),由全等三角形的性质得出∠BAG=∠DAE,由折叠的性质得出∠DAE=∠FAE,∠AED=∠AEF,由三角形内角和定理可得出答案.
【详解】解:∵四边形ABCD是菱形,
∴AB=AD,∠B=∠D=60°,
∴∠BAD=120°,
在△ABG和△ADE中,
,
∴△ABG≌△ADE(SAS),
∴∠BAG=∠DAE,
∵将△ADE沿AE折叠,
∴∠DAE=∠FAE,∠AED=∠AEF,
∴∠DAE=∠BAD=40°,
∴∠AED=180°-∠DAE-∠D=180°-40°-60°=80°,
∴∠FEC=180°2∠AED=180°160°=20°,
故答案为:20°.
【点睛】本题考查了菱形的性质,折叠的性质,全等三角形的判定与性质,熟练掌握折叠的性质是解题的关键.
22. 2
【分析】(1)根据折叠的性质知EC=BC-BE=6-4=2;
(2)当B'落在DE上时,作AH⊥DE于H,由折叠的性质可证AD=DE,再利用△AB'H是含30°的直角三角形,从而求出DB'的长,即可解决问题.
【详解】(1)∵将△ABE沿AE折叠,点B′是点B的对应点,
∴AB=AB’, ∠B=∠AB'E,
∵四边形ABCD是平行四边形,
∴∠B=∠ADC,AB∥CD,AD∥BC,
∴∠AB’E=∠ADC,
∴B’E∥CD,
∴B’E∥AB,
∴四边形ABEB’是平行四边形,
∵AB=AB’,
四边形ABEB'是菱形,
∴EC=BC-BE=6-4=2,
故答案为:2;
(2)如图,当B'落在DE上时,作AH⊥DE于H,
在Rt△AHB'中,
∵∠AB'H=60°,AB'=4,
∴HB'=AB′=2,AH=HB′=,
在Rt△ADH中,
,
∵AD∥BC,
∴∠DAE=∠AEB=∠AED,
∴DA=DE=6,
∴,
∴,
∴若点B′落在△ADE内(包括边界),则x的取值范围是,
故答案为:.
【点睛】本题主要考查了平行四边形的性质,翻折变换,含30°角的直角三角形的性质等知识,找到临界状态求出x的长是解题的关键.
23.8
【分析】由折叠得到,结合矩形的性质,解得,继而证明四边形是菱形,由菱形对角线的性质结合菱形的面积解得,最后在中,利用勾股定理解得的长即可.
【详解】解:由折叠的性质可知
连接,与相交于点,
折叠
四边形是菱形,
中,
设
在中,
故答案为:8.
【点睛】本题考查矩形与折叠、菱形的判定与性质、勾股定理等知识,是重要考点,难度较易,掌握相关知识是解题关键.
24.6°
【分析】首先根据折叠的性质得出,然后根据菱形的性质求出的度数,最后利用求解即可.
【详解】根据折叠的性质有,
.
∵四边形ABCD是菱形,
,
,
,
,
,
故答案为:6°.
【点睛】本题主要考查菱形的性质和折叠的性质,掌握菱形的性质和折叠的性质是解题的关键.
25.22.5°
【分析】根据翻折变换的性质可得AB=AF,然后根据等腰三角形两底角相等求出∠B=∠AFE=75°,可得∠C,根据AF=AD,求出∠AFD,由三角形外角等于不相邻的两个内角的和即可得答案.
【详解】解:∵菱形ABCD沿AE折叠,B落在BC边上的点F处,
∴AD=AB=AF,∠AEB=90°=∠AEF,∠FAE=∠BAE=15°,
∴∠B=∠AFE=75°,
在菱形ABCD中,AB∥CD,AD∥BC,
∴∠DAF=∠AFE=75°,∠C=180°-∠B=105°,
∵AF=AD,
∴∠ADF=∠AFD==52.5°,
∴∠DFB=∠AFE+∠AFD=127.5°,
∴∠FDC=∠DFB-∠B=22.5°,
故答案为:22.5°.
【点睛】本题考查了菱形中的翻折问题,等腰三角形的性质,解题的关键是掌握翻折的性质及菱形的性质.
26.6或8##8或6
【分析】由折叠的性质可得,再根据已知条件推出,设,则,在中,由勾股定理得:,即,据此求解即可.
【详解】解:由折叠的性质可得,
∵,
∴,
∵四边形是正方形且边长为12,
∴,
∴,
∴,
设,则,
在中,由勾股定理得:,
∴,
解得或,
∴的长为6或8,
故答案为:6或8.
【点睛】本题主要考查了折叠的性质,正方形的性质,勾股定理,推出是解题的关键.
27.##
【分析】根据正方形的性质与折叠的性质可得,设,则,勾股定理即可求解.
【详解】解:∵四边形是正方形,
∴,,
,
是等腰直角三角形,
设,则,,
在中,,
,
解得,
故答案为:.
【点睛】本题考查了正方形的折叠问题,掌握正方形的性质与折叠的性质是解题的关键.
28.
【分析】设正方形的边长为a,根据折叠得出,,根据勾股定理列出关于a的方程,解方程即可.
【详解】解:设正方形的边长为a,则根据折叠可知,,,
在Rt△BFN中,根据勾股定理可知,,
即:,
解得:或(舍去).
故答案为:.
【点睛】本题主要考查了正方形的折叠问题,勾股定理的应用,设出正方形的边长,根据勾股定理列出关于a的方程,是解题的关键.
29.
【分析】设DF=EF=x,分别表示出DA=DC= 、AC= ,利用勾股定理列方程解得,利用等积法求出结果.
【详解】解:由折叠知AF平分∠DAE,∠D=90°,FE⊥AC于于点F,
∴FD=FE,
设DF=EF=x,
在直角△EFC中,∠FCE=45°,
∴EC=EF=x,
∴FC= ,
∴DA=DC= ,
∴AC= ,
在直角△ADF中,
∴AD2+DF2=AF2,
即 ,
解得 ,
又∵ ,
∴,
故答案为 .
【点睛】本题考查正方形的性质、勾股定理以及等积法的应用,解决问题的关键是利用三角形的面积有两种不同的表示方法确定等量关系.
30. 1 45 3
【分析】(1)由翻折的性质及全等三角形的性质可求出AG=FG;
(2)根据正方形的性质及角的和差关系可得;
(3)设边长为x,得到BG=x-1,BE=,GE=1+,根据勾股定理列出方程,故可求解.
【详解】(1)根据折叠的意义,得△DEC≌△DEF,
∴EF=EC,DF=DC,∠CDE=∠FDE,
∵DA=DF,DG=DG,
∴Rt△ADG≌Rt△FDG(HL),
∴∠ADG=∠FDG,AG=FG=1
(2)∵△DEC≌△DEF,Rt△ADG≌Rt△FDG
∴∠GDE=∠FDG+∠FDE=(∠ADF+∠CDF)=45°
(3)∵△DEC≌△DEF,Rt△ADG≌Rt△FDG
∴GF=GA=1,EC=EF
设正方形边长为x,得到BG=x-1,BE=,GE=1+,
在Rt△BEG中,GE2=BG2+BE2
∴(1+)2=(x-1)2+()2
解得x=3
∴正方形的边长为3
故答案为:1;45;3.
【点睛】此题考查了翻折性质、正方形的性质、全等三角形的判定与性质等,掌握其性质是解决此题关键.
31.(1)是直角三角形,理由见解析
(2)
【分析】(1)利用翻折变换的性质及矩形的性质即可求解;
(2)利用翻折变换的性质即可求解.
【详解】(1)是直角三角形,
∵四边形是矩形,
∴,
∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴是直角三角形;
(2)∵将矩形纸片沿折叠,使点A落在点E处,
∴,
∴四边形是矩形,,
∴,
∴.
【点睛】本题考查了折叠的性质,矩形的性质,掌握折叠的性质是解题的关键.
32.
【分析】根据勾股定理求出的长;进而求出的长度;由题意得;利用勾股定理列出关于的方程,解方程即可解决问题.
【详解】解:四边形为矩形,
,,;
折叠矩形的一边,使点落在边的点处,
,
由勾股定理得:,
,
;
设,;
在中,由勾股定理得:,
解得:,
.
【点睛】本题主要考查了翻折变换的性质及其应用问题,解题的关键是掌握折叠的性质,熟练运用勾股定理列方程解决问题.
33.(1);
(2).
【分析】(1)由折叠的性质可得:,利用勾股定理求解即可;
(2)由(1)可得,设,则利用勾股定理求解即可.
【详解】(1)解:由矩形的性质可得:,,
由折叠的性质可得:,
由勾股定理可得:;
(2)解:由(1)可得,
设,则,
在中,,即
解得,即.
【点睛】此题考查了矩形的折叠问题,涉及了勾股定理,解题的关键是能够利用勾股定理灵活求解.
34..
【分析】利用对称的性质得出,进而得出,证明四边形是菱形,再利用菱形的性质结合勾股定理得出答案.
【详解】解:∵B、E两点关于直线对称,
∴,
在矩形中,,
∴,
∴,
∴,
∴,
∴四边形是菱形;
设菱形的边长为x,
∴,
在中,,
∴,
∴解得:.
∴.
【点睛】此题主要考查了菱形的判定与性质以及勾股定理,正确应用轴对称的性质是解题关键.
35.(1)见解析
(2)菱形BEDF的面积为.
【分析】(1)证明△OBF≌△ODE,得到OB=OD即可得出结论;
(2)由ED=2AE,由AB AD=,求得S△ABD=AB AD=,再由ED=2AE,可求得S△BDE=,进而可得出菱形BEDF的面积.
【详解】(1)证明:将△BED沿BD折叠,使E,F重合,
∴OE=OF,EF⊥BD,
∵四边形ABCD是矩形,
∴∠C=90°,AD∥BC,
∴∠ODE=∠OBF,
在△OBF和△ODE中,
,
∴△OBF≌△ODE(AAS),
∴OB=OD,
∵OE=OF,
∴四边形BFDE是平行四边形,
∵EF⊥BD,
∴四边形BFDE是菱形;
(2)解:∵AB AD=,
∴S△ABD=AB AD=,
∵ED=2AE,
∴ED=AD,
∴S△BDE:S△ABD=2:3,
∴S△BDE=,
∴菱形BEDF的面积=2S△BDE=.
【点睛】本题考查了翻折变换的性质、菱形的判定与性质、矩形的性质等知识;熟练掌握菱形的判定与性质是解题的关键.
36.(1)见解析
(2)4
(3)
【分析】(1)根据折叠的性质可得BM=DM,DN=BN,∠DMN=∠BMN,再由四边形ABCD是矩形,可得AB∥CD,从而得到∠DNM=∠BMN,进而得到∠DNM=∠DMN,继而得到DM=DN,即可求证;
(2)设AM=x,则DM=BM=AB-AM=9-x,在中,由勾股定理,即可求解;
(3)连接BD,由勾股定理可得,再根据,即可求解.
【详解】(1)证明:根据题意得:BM=DM,DN=BN,∠DMN=∠BMN,
∵四边形ABCD是矩形,
∴AB∥CD,
∴∠DNM=∠BMN,
∴∠DNM=∠DMN,
∴DM=DN,
∴DM=BM=DN=BN,
∴四边形DMBN是菱形;
(2)解:设AM=x,则DM=BM=AB-AM=9-x,
∵四边形ABCD是矩形,
∴∠A=90°,
在中,,
∴,解得:x=4,
即AM=4;
(3)解:如图,连接BD,
∵四边形ABCD是矩形,
∴∠A=90°,
在中, AB=9,AD=3,
∴,
由(2)得:AM=4,
∴BM=5,
∵,
∴,
解得:.
【点睛】本题主要考查了矩形的性质,菱形的判定和性质,勾股定理,折叠的性质,熟练掌握矩形的性质,菱形的判定和性质,勾股定理,折叠的性质是解题的关键.
37.[问题原型] 见解析;
[结论应用](1);(2)(3)
【分析】[问题原型] 由等腰三角形的性质可得,,由三角形内角和定理可得结论;
[结论应用]
(1)根据轴对称的性质得出;
(2)根据平行线的性质即可求解;
(3)证明,设,在中,勾股定理列出方程,解方程即可求解.
【详解】[问题原型]证明:是边的中线,.
,
,,
,
,
;
[结论应用](1)依题意点、的对应点分别为点、
∴关于对称,
∴,
(2)∵为中点,
由[问题原型]可得
又,
∴,
∵,
∴;
(3)∵四边形是正方形,
∴,
∵折叠,
∴,,
∴,
∵为中点,
∴,
∴,
在与中,
∴,
设,
在中,,
,,
∵,
∴,
解得,
即.
【点睛】本题考查了折叠的性质,等腰三角形的性质与判定,平行线的性质,平行四边形的性质,正方形的性质,勾股定理,掌握折叠的的性质是解题的关键.
38.(1)见解析
(2)GF的值为.
【分析】(1)先判断出AF=BE,进而得出△FAB≌△EBC(SAS),即可得出结论;
(2)连接BG,根据HL证明Rt△BQG≌Rt△BCG,得QG=GC,设QG=b,在Rt△DFG中,根据勾股定理列方程可得b,从而可得结论.
【详解】(1)证明:∵四边形ABCD是正方形,
∴AB=AD,∠A=∠ABC=90°,
∵E、F分别是正方形ABCD边AB、AD的中点,
∵AF=BE,
∴△FAB≌△EBC(SAS),
∴CE=BF;
(2)解:如图,连接BG,
由折叠得:AB=BQ,∠BQF=∠A=90°,
∵AB=BC,
∴BC=BQ,
∵BG=BG,
∴Rt△BQG≌Rt△BCG(HL),
∴QG=GC,
∵AB=4,F是正方形ABCD边AD的中点,
设QG=b,
则DF=AF=FQ=2,FG=2+b,DG=4-b,
在Rt△DFG中,∵DF2+DG2=FG2,
∴,
∴b=,即QG=,
∴GF=FQ+QG=2+=.
∴GF的值为.
【点睛】此题主要考查了正方形的性质,全等三角形的判定和性质,勾股定理等知识,正确作辅助线是本题的关键.
39.(1)CN=3;(2)正方形的面积为80
【分析】(1)根据题意易得DN=NE,BE=EC=4,设CN=x,则有DN=8-x,然后根据勾股定理进行求解即可;
(2)过点M作MG⊥CD于点G,连接DE,证明△MNG≌△DEC,则有MN=DE,进而根据勾股定理及正方形的面积公式可求解.
【详解】解:(1)∵将边长为8的正方形ABCD折叠,使点D落在BC边的中点E处,
∴DN=NE,BE=EC=4,
设CN=x,则有DN=8-x,
∴在Rt△ECN中,,即,
解得,即CN=3;
(2)过点M作MG⊥CD于点G,连接DE,交MN于点H,如图所示:
由题意可得AM=DG,MG=BC=CD,∠MGN=∠C=90°,
根据折叠的性质可得:DE⊥MN,
∴∠NMG+∠MHE=90°,
∵∠EDC+∠DHG=90°,∠DHG=∠MHE,
∴∠NMG=∠EDC,
∴△MNG≌△DEC(ASA),
∴MN=DE,
在Rt△DEC中,,
∴,
∴以MN为边的正方形面积为:.
【点睛】本题主要考查正方形的性质、折叠的性质、全等三角形的性质与判定及勾股定理,熟练掌握正方形的性质、折叠的性质、全等三角形的性质与判定及勾股定理是解题的关键.
答案第1页,共2页
答案第1页,共2页
