24.1.4 圆周角 学案(无答案)
文档属性
| 名称 | 24.1.4 圆周角 学案(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 00:00:00 | ||
图片预览

文档简介
【编号:15】初三上学期 24章《圆》导学案 24.1.4 圆周角
24.1.4 圆周角
目标导学
理解圆周角的概念,会叙述并证明圆周角定理.
理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
理解掌握圆周角定理的推论及其证明过程和运用.(难点)
二、知识回顾
如图,AB,CD为⊙O的两条弦,AB=CD. 求证:∠AOC=∠BOD.
新知导入
观察右下图,发现∠ACB的顶点不在圆心,在圆周上,你知道∠ACB这一类角的名称吗?
四、新知探究
探究一:圆周角的概念
圆周角:顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角。
如右图:∠ACB为圆周角
同一个弧所对的圆周角有________个。
跟踪训练:
1、如图所示,∠BAC 是圆周角的是( )
2、如右上图所示,图中的圆周角共有______个,其中弧AB所对的圆周角是____________,弧CD所对的圆周角是___________。
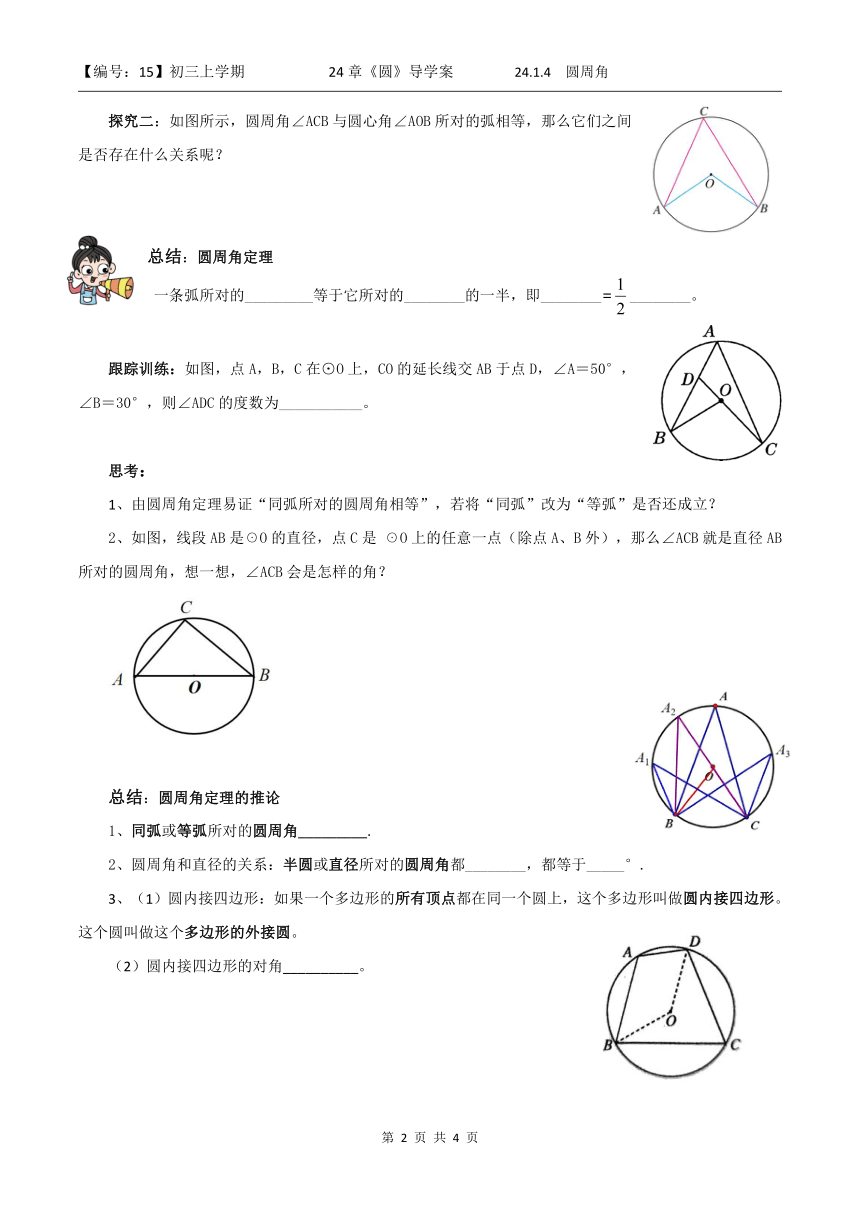
探究二:如图所示,圆周角∠ACB与圆心角∠AOB所对的弧相等,那么它们之间是否存在什么关系呢?
总结:圆周角定理
一条弧所对的_________等于它所对的________的一半,即________=________。
跟踪训练:如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为___________。
思考:
1、由圆周角定理易证“同弧所对的圆周角相等”,若将“同弧”改为“等弧”是否还成立?
2、如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
总结:圆周角定理的推论
1、同弧或等弧所对的圆周角_________.
2、圆周角和直径的关系:半圆或直径所对的圆周角都________,都等于_____°.
3、(1)圆内接四边形:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接四边形。这个圆叫做这个多边形的外接圆。
(2)圆内接四边形的对角__________。
五、经典例题
1、如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线。
写出相等的角。
2、如图,⊙O的直径AB为10 cm,弦AC为6 cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
六、当堂达标
1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
(1) (2) (3)
2.如图2,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
3.如图3,AD是⊙O的直径,AC是弦,OB⊥AD,若OB=5,且∠CAD=30°,则BC等于( ).
A.3 B.3+ C.5- D.5
4.半径为2a的⊙O中,弦AB的长为2a,则弦AB所对的圆周角的度数是________.
5.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.
(4) (5)
6.如图5,已知△ABC为⊙O内接三角形,BC=1,∠A=60°,则⊙O半径为_______.
7.如图,弦AB把圆周分成1:2的两部分,已知⊙O半径为1,求弦长AB.
8.如图,已知AB=AC,∠APC=60°
(1)求证:△ABC是等边三角形.
(2)若BC=4cm,求⊙O的面积.
七、课后总结
24.1.4 圆周角
目标导学
理解圆周角的概念,会叙述并证明圆周角定理.
理解圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.(重点、难点)
理解掌握圆周角定理的推论及其证明过程和运用.(难点)
二、知识回顾
如图,AB,CD为⊙O的两条弦,AB=CD. 求证:∠AOC=∠BOD.
新知导入
观察右下图,发现∠ACB的顶点不在圆心,在圆周上,你知道∠ACB这一类角的名称吗?
四、新知探究
探究一:圆周角的概念
圆周角:顶点在圆上,并且两边都与圆相交,这样的角叫做圆周角。
如右图:∠ACB为圆周角
同一个弧所对的圆周角有________个。
跟踪训练:
1、如图所示,∠BAC 是圆周角的是( )
2、如右上图所示,图中的圆周角共有______个,其中弧AB所对的圆周角是____________,弧CD所对的圆周角是___________。
探究二:如图所示,圆周角∠ACB与圆心角∠AOB所对的弧相等,那么它们之间是否存在什么关系呢?
总结:圆周角定理
一条弧所对的_________等于它所对的________的一半,即________=________。
跟踪训练:如图,点A,B,C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,则∠ADC的度数为___________。
思考:
1、由圆周角定理易证“同弧所对的圆周角相等”,若将“同弧”改为“等弧”是否还成立?
2、如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
总结:圆周角定理的推论
1、同弧或等弧所对的圆周角_________.
2、圆周角和直径的关系:半圆或直径所对的圆周角都________,都等于_____°.
3、(1)圆内接四边形:如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接四边形。这个圆叫做这个多边形的外接圆。
(2)圆内接四边形的对角__________。
五、经典例题
1、如图,点A、B、C、D在同一个圆上,AC、BD为四边形ABCD的对角线。
写出相等的角。
2、如图,⊙O的直径AB为10 cm,弦AC为6 cm,∠ACB的平分线交⊙O于D,求BC,AD,BD的长.
六、当堂达标
1.如图1,A、B、C三点在⊙O上,∠AOC=100°,则∠ABC等于( ).
A.140° B.110° C.120° D.130°
(1) (2) (3)
2.如图2,∠1、∠2、∠3、∠4的大小关系是( )
A.∠4<∠1<∠2<∠3 B.∠4<∠1=∠3<∠2 C.∠4<∠1<∠3∠2 D.∠4<∠1<∠3=∠2
3.如图3,AD是⊙O的直径,AC是弦,OB⊥AD,若OB=5,且∠CAD=30°,则BC等于( ).
A.3 B.3+ C.5- D.5
4.半径为2a的⊙O中,弦AB的长为2a,则弦AB所对的圆周角的度数是________.
5.如图4,A、B是⊙O的直径,C、D、E都是圆上的点,则∠1+∠2=_______.
(4) (5)
6.如图5,已知△ABC为⊙O内接三角形,BC=1,∠A=60°,则⊙O半径为_______.
7.如图,弦AB把圆周分成1:2的两部分,已知⊙O半径为1,求弦长AB.
8.如图,已知AB=AC,∠APC=60°
(1)求证:△ABC是等边三角形.
(2)若BC=4cm,求⊙O的面积.
七、课后总结
同课章节目录
