数学人教A版(2019)选择性必修第一册 3.2.1双曲线及其标准方程 课件(共25张ppt)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第一册 3.2.1双曲线及其标准方程 课件(共25张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 10:59:29 | ||
图片预览




文档简介
(共25张PPT)
3.2.1 双曲线及其标准方程
情境引入
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定位等都要用到双曲线的性质.本节我们将类比椭圆的研究方法研究双曲线的有关问题.
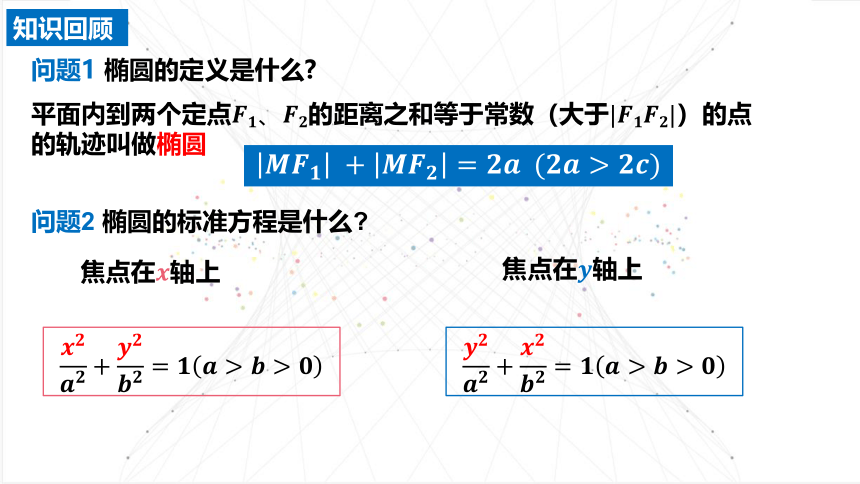
知识回顾
问题1 椭圆的定义是什么
平面内到两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆
问题2 椭圆的标准方程是什么
焦点在轴上
焦点在轴上
问题2:平面内与两个定点的距离的差等于常数的点的轨迹是什么?
新知探究
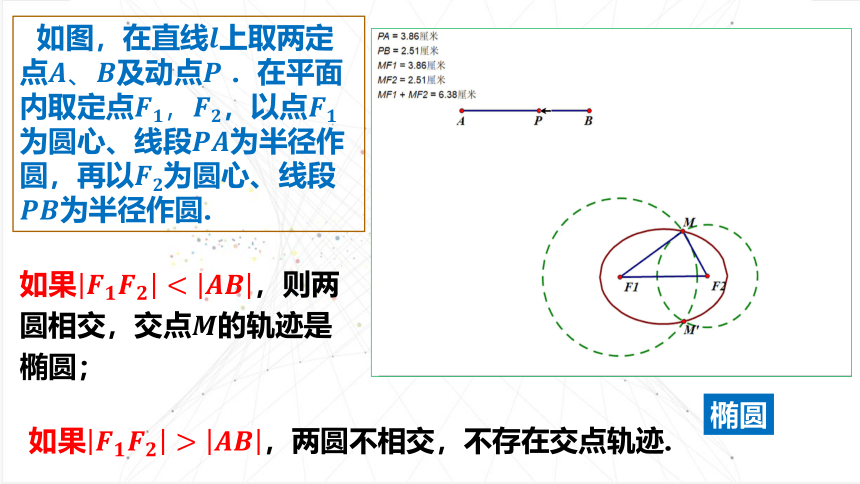
下面先用信息技术探究一下
如图,在直线上取两定点及动点.在平面内取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
椭圆
如果,则两圆相交,交点的轨迹是椭圆;
如果,两圆不相交,不存在交点轨迹.
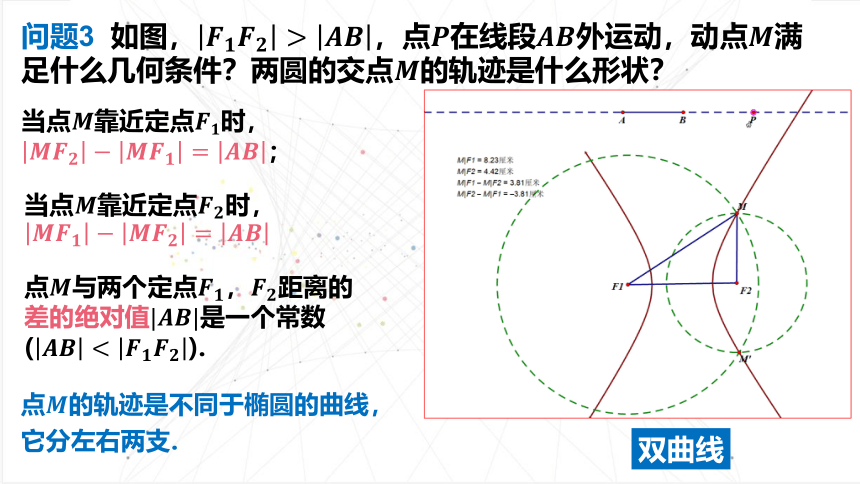
问题3 如图,,点在线段外运动,动点满足什么几何条件?两圆的交点的轨迹是什么形状?
双曲线
点的轨迹是不同于椭圆的曲线,它分左右两支.
当点靠近定点时,;
当点靠近定点时,
点与两个定点,距离的差的绝对值是一个常数
().
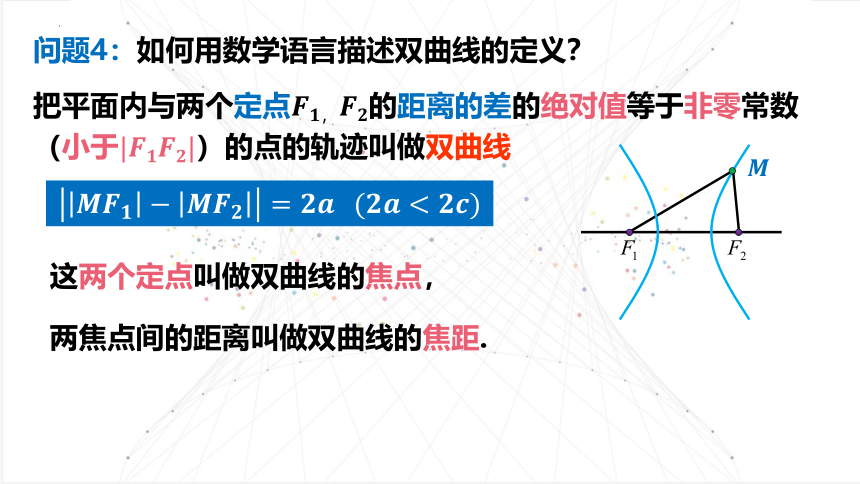
问题4:如何用数学语言描述双曲线的定义?
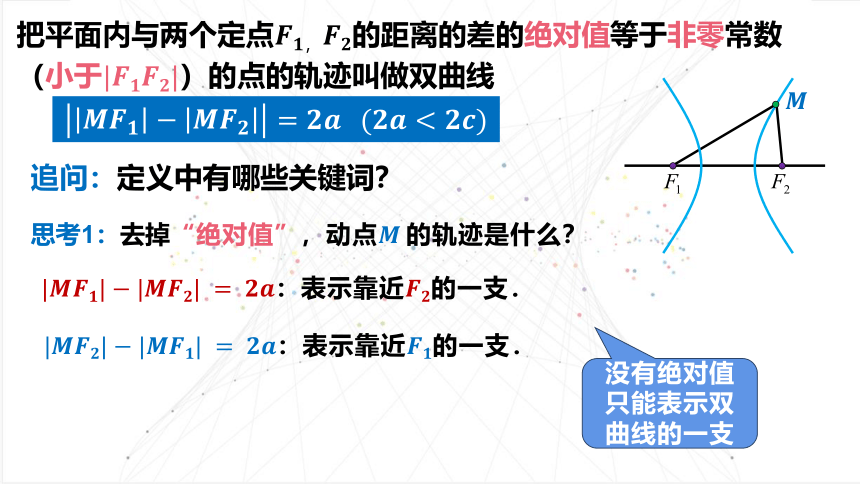
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
追问:定义中有哪些关键词?
思考1:去掉“绝对值”,动点的轨迹是什么?
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
:表示靠近的一支.
:表示靠近的一支.
没有绝对值只能表示双曲线的一支
思考2:如果“常数为”,动点的轨迹是什么?
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
点轨迹为中垂线.
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
思考3:如果,那么动点的轨迹是什么?
表示以为端点的两条射线.
如果,动点的轨迹又是什么?
轨迹不存在
问题4 类比求椭圆标准方程的过程,如何建立适当的坐标系,得出双曲线的方程?
对称性,直线是它的一条对称轴
建系
化简
列式
设点
以直线为轴,线段的垂直平分线为轴,建立如图所示平面直角坐标系.
l
由双曲线的定义得
类比椭圆标准方程的化简过程,化简得
两边同时除以,得
由双曲线定义知,,即,所以.
令,其中,代入上式,
得.
焦点在轴上
双曲线的标准方程
焦点分别是,
思考: 大小关系如何?
思考:类比焦点在轴上的椭圆标准方程,焦点在轴上的双曲线的把标准方程是什么?
l
焦点,的坐标分别是,
的意义同上,这个方程也是双曲线的标准方程.
焦点在轴上:
焦点在轴上:
(1)左边是两个分式的平方差,右边是1;
双曲线的标准方程的特点:
(2)系数为正的项的分母是 ,系数为负的项的分母是
与哪一个系数为正,焦点就在哪一个轴上
概念辨析
辨析1.判断正误.
(1)在双曲线标准方程中,,,且.( )
(2)方程表示焦点在轴上的双曲线.( )
(3)方程表示双曲线.( )
×
×
√
C
辨析2. 若动点到点,的距离之差的绝对值为,则点的轨迹是( ).
A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
练习 求下列双曲线的焦点坐标,以及双曲线上任一点到两个焦点的距离之差的绝对值
(1)焦点坐标为,. 距离之差的绝对值为
(2)焦点坐标为,
(3)焦点坐标为,
双曲线与椭圆的区别与联系
定 义
方 程
焦 点
a.b.c的关系 椭 圆
双曲线
|MF1|+|MF2|=2a
||MF1|-|MF2||=2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
a>b>0,a2=b2+c2
a>0,b>0,但a不一定大于b,c2=a2+b2
例题精讲
例1.已知双曲线的两个焦点分别为,,双曲线上一点与,的距离差的绝对值等于,求双曲线的标准方程.
l
解:由于椭圆的焦点在轴上,所以设它的标准方程为
.
由得又,
因此
所以,双曲线的标准方程为.
例2.已知,两地相距,在地听到炮弹爆炸声比在地晚,且声速为,求炮弹爆炸点的轨迹方程.
l
解:如图,建立平面直角坐标系,使两点在轴上,并且原点与线段的中点重合.
设炮弹爆炸点的坐标为,
则,即.
又,所以,,.
所以,炮弹爆炸点的轨迹方程为
因为,所以点的轨迹是双曲线的右支,因此
例题精讲
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程,并由点的轨迹方程判断轨迹的形状,与例比较,你有什么发现?
化简整理,得
因此,点的轨迹是焦点在轴上的双曲线(除两点外).
解:设则,.
由题意知,即
规律总结:若一个动点与两个定点连线的斜率之积为一个常数.
当时,轨迹为双曲线(除,两点外),方程为;
当时,轨迹为椭圆(除,两点外),方程为;
当时,轨迹为圆(除两点外),方程为.
3.已知方程表示双曲线,求的取值范围.
课堂练习
4. 双曲线的两个焦点分别是与焦距为8;是双曲线上的一点,且,求的值.
双曲线的定义
课堂小结
图像
标准方程
3.2.1 双曲线及其标准方程
情境引入
双曲线也是具有广泛应用的一种圆锥曲线,如发电厂冷却塔的外形、通过声音时差测定位等都要用到双曲线的性质.本节我们将类比椭圆的研究方法研究双曲线的有关问题.
知识回顾
问题1 椭圆的定义是什么
平面内到两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆
问题2 椭圆的标准方程是什么
焦点在轴上
焦点在轴上
问题2:平面内与两个定点的距离的差等于常数的点的轨迹是什么?
新知探究
下面先用信息技术探究一下
如图,在直线上取两定点及动点.在平面内取定点,以点为圆心、线段为半径作圆,再以为圆心、线段为半径作圆.
椭圆
如果,则两圆相交,交点的轨迹是椭圆;
如果,两圆不相交,不存在交点轨迹.
问题3 如图,,点在线段外运动,动点满足什么几何条件?两圆的交点的轨迹是什么形状?
双曲线
点的轨迹是不同于椭圆的曲线,它分左右两支.
当点靠近定点时,;
当点靠近定点时,
点与两个定点,距离的差的绝对值是一个常数
().
问题4:如何用数学语言描述双曲线的定义?
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
这两个定点叫做双曲线的焦点,
两焦点间的距离叫做双曲线的焦距.
追问:定义中有哪些关键词?
思考1:去掉“绝对值”,动点的轨迹是什么?
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
:表示靠近的一支.
:表示靠近的一支.
没有绝对值只能表示双曲线的一支
思考2:如果“常数为”,动点的轨迹是什么?
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
点轨迹为中垂线.
把平面内与两个定点的距离的差的绝对值等于非零常数(小于)的点的轨迹叫做双曲线
思考3:如果,那么动点的轨迹是什么?
表示以为端点的两条射线.
如果,动点的轨迹又是什么?
轨迹不存在
问题4 类比求椭圆标准方程的过程,如何建立适当的坐标系,得出双曲线的方程?
对称性,直线是它的一条对称轴
建系
化简
列式
设点
以直线为轴,线段的垂直平分线为轴,建立如图所示平面直角坐标系.
l
由双曲线的定义得
类比椭圆标准方程的化简过程,化简得
两边同时除以,得
由双曲线定义知,,即,所以.
令,其中,代入上式,
得.
焦点在轴上
双曲线的标准方程
焦点分别是,
思考: 大小关系如何?
思考:类比焦点在轴上的椭圆标准方程,焦点在轴上的双曲线的把标准方程是什么?
l
焦点,的坐标分别是,
的意义同上,这个方程也是双曲线的标准方程.
焦点在轴上:
焦点在轴上:
(1)左边是两个分式的平方差,右边是1;
双曲线的标准方程的特点:
(2)系数为正的项的分母是 ,系数为负的项的分母是
与哪一个系数为正,焦点就在哪一个轴上
概念辨析
辨析1.判断正误.
(1)在双曲线标准方程中,,,且.( )
(2)方程表示焦点在轴上的双曲线.( )
(3)方程表示双曲线.( )
×
×
√
C
辨析2. 若动点到点,的距离之差的绝对值为,则点的轨迹是( ).
A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
练习 求下列双曲线的焦点坐标,以及双曲线上任一点到两个焦点的距离之差的绝对值
(1)焦点坐标为,. 距离之差的绝对值为
(2)焦点坐标为,
(3)焦点坐标为,
双曲线与椭圆的区别与联系
定 义
方 程
焦 点
a.b.c的关系 椭 圆
双曲线
|MF1|+|MF2|=2a
||MF1|-|MF2||=2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
a>b>0,a2=b2+c2
a>0,b>0,但a不一定大于b,c2=a2+b2
例题精讲
例1.已知双曲线的两个焦点分别为,,双曲线上一点与,的距离差的绝对值等于,求双曲线的标准方程.
l
解:由于椭圆的焦点在轴上,所以设它的标准方程为
.
由得又,
因此
所以,双曲线的标准方程为.
例2.已知,两地相距,在地听到炮弹爆炸声比在地晚,且声速为,求炮弹爆炸点的轨迹方程.
l
解:如图,建立平面直角坐标系,使两点在轴上,并且原点与线段的中点重合.
设炮弹爆炸点的坐标为,
则,即.
又,所以,,.
所以,炮弹爆炸点的轨迹方程为
因为,所以点的轨迹是双曲线的右支,因此
例题精讲
问题3:如图,点的坐标分别是,直线相交于点,且它们的斜率之积是,试求点的轨迹方程,并由点的轨迹方程判断轨迹的形状,与例比较,你有什么发现?
化简整理,得
因此,点的轨迹是焦点在轴上的双曲线(除两点外).
解:设则,.
由题意知,即
规律总结:若一个动点与两个定点连线的斜率之积为一个常数.
当时,轨迹为双曲线(除,两点外),方程为;
当时,轨迹为椭圆(除,两点外),方程为;
当时,轨迹为圆(除两点外),方程为.
3.已知方程表示双曲线,求的取值范围.
课堂练习
4. 双曲线的两个焦点分别是与焦距为8;是双曲线上的一点,且,求的值.
双曲线的定义
课堂小结
图像
标准方程
