第五章 一元一次方程专项拓展训练(四) 2023-2024学年冀教版数学七年级上册(含解析)
文档属性
| 名称 | 第五章 一元一次方程专项拓展训练(四) 2023-2024学年冀教版数学七年级上册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 303.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 00:00:00 | ||
图片预览



文档简介
《第五章 一元一次方程》专项拓展训练(四)
专项一 解一元一次方程
1. 下列方程变形正确的是 ( )
A.将方程3x-2=2x-1移项,得3x-2x=-1-2
B.将方程3-x=2-5(x-1)去括号,得3-x=2-5x-1
C.方程=1可化简为3x=6
D.将方程x=系数化为1,得x=-1
2. 解下列方程:
(1)2x+5=3(x-1);
(2)3(x+1)-2(x+2)=2x+3;
(3);
(4).
3.如图是小慧同学书写的解方程=1的过程,请你认真阅读并回答下列问题:
(1)同学们看了小慧的解答过程,都说她做错了,你认为小慧同学从第 步开始出错,错误原因是 .
(2)请你写出正确的解答过程.
专项二 一元一次方程的实际应用
类型1 数学文化问题
1. 我国古代名著《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问人数几何.原文意思是:现在有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人.如果假设共有x人,那么可列方程为 ( )
A.8x+3=7x+4 B.8x-3=7x+4
C.8x+3=7x-4 D.8x-3=7x-4
2. 我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马再从原地出发,几天可以追上慢马 设快马x天可以追上慢马,根据题意,可列方程为 .
类型2 月历问题
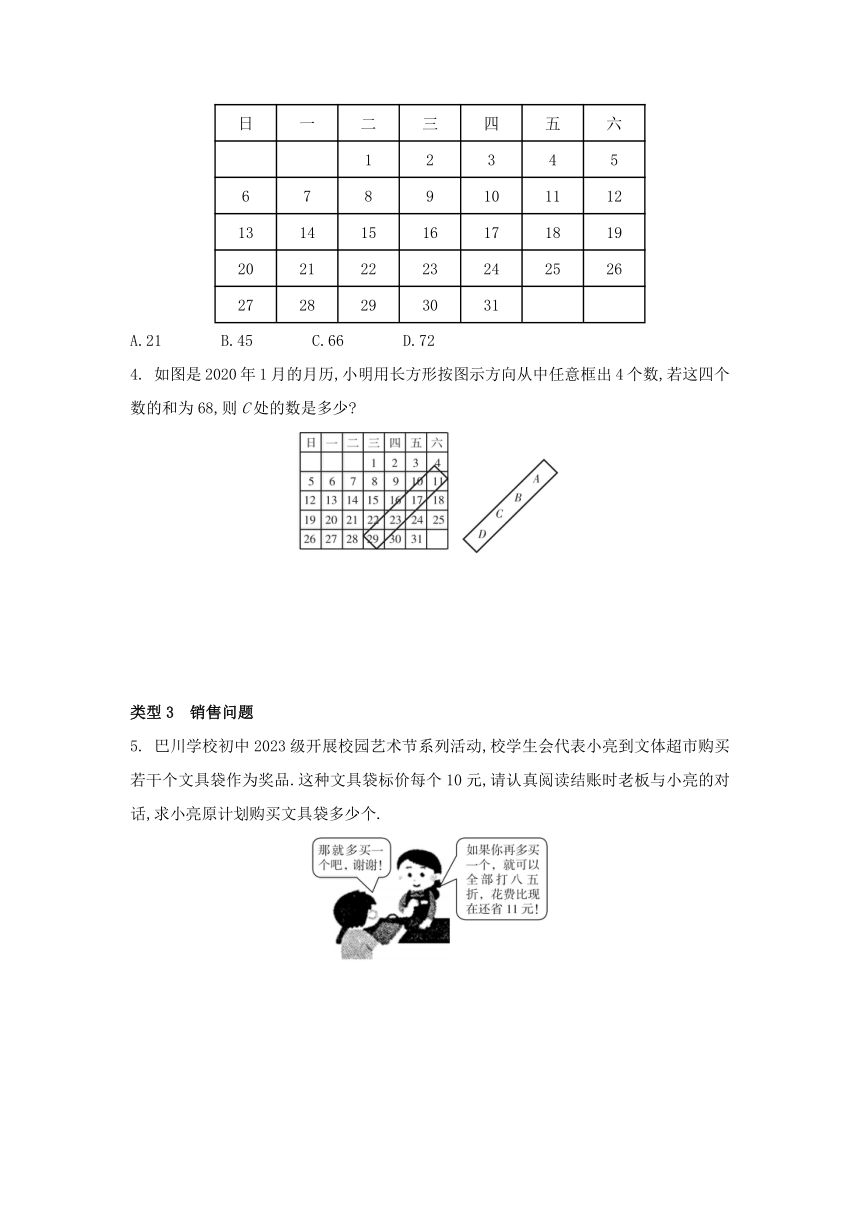
3. 如图,在某年1月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
A.21 B.45 C.66 D.72
4. 如图是2020年1月的月历,小明用长方形按图示方向从中任意框出4个数,若这四个数的和为68,则C处的数是多少
类型3 销售问题
5. 巴川学校初中2023级开展校园艺术节系列活动,校学生会代表小亮到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小亮的对话,求小亮原计划购买文具袋多少个.
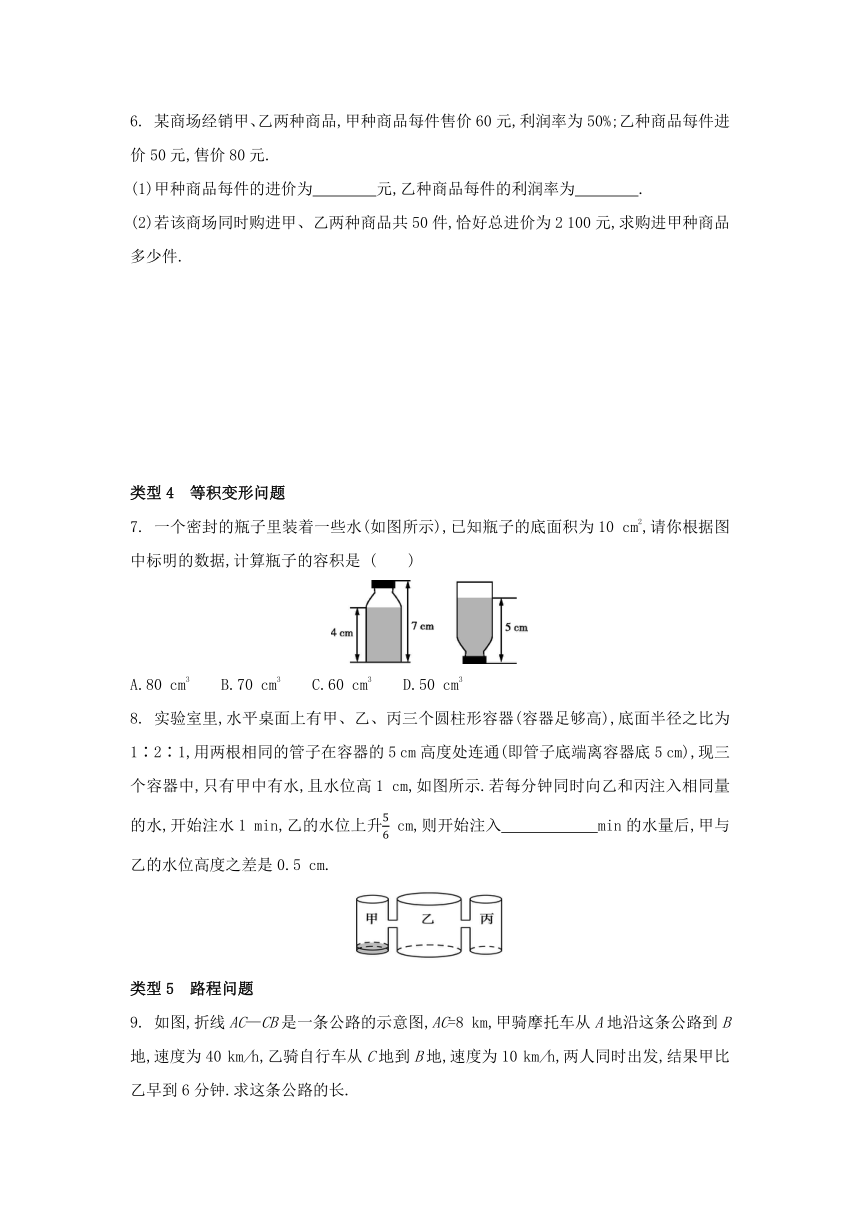
6. 某商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.
(1)甲种商品每件的进价为 元,乙种商品每件的利润率为 .
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2 100元,求购进甲种商品多少件.
类型4 等积变形问题
7. 一个密封的瓶子里装着一些水(如图所示),已知瓶子的底面积为10 cm2,请你根据图中标明的数据,计算瓶子的容积是 ( )
A.80 cm3 B.70 cm3 C.60 cm3 D.50 cm3
8. 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两根相同的管子在容器的5 cm高度处连通(即管子底端离容器底5 cm),现三个容器中,只有甲中有水,且水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1 min,乙的水位上升 cm,则开始注入 min的水量后,甲与乙的水位高度之差是0.5 cm.
类型5 路程问题
9. 如图,折线AC—CB是一条公路的示意图,AC=8 km,甲骑摩托车从A地沿这条公路到B地,速度为40 km/h,乙骑自行车从C地到B地,速度为10 km/h,两人同时出发,结果甲比乙早到6分钟.求这条公路的长.
10. 为了治理污染,改善空气质量,现在广大农村正在实施“煤改气”工程.甲、乙两个工程队共同承接了某村“燃气壁挂炉注水”任务.若甲队单独施工,则需10天完成;若乙队单独施工,则需15天完成.
(1)若甲、乙两队合作,需要几天完成
(2)若甲队先施工5天,剩下部分由两队合作完成,还需要几天
11. 如图,某市A,B两地之间有两条公路,一条是市区公路AB,另一条是外环公路AD—DC—CB.这两条公路围成等腰梯形ABCD,其中DC∥AB,AB∶AD∶DC=10∶5∶2.
(1)求外环公路总长和市区公路长的比.
(2)某人驾车从A地出发,沿市区公路去B地,平均速度是40 km/h.返回时沿外环公路行驶,平均速度是80 km/h,结果比去时少用了 h,求市区公路的长.
类型6 计费问题
12. 为了加强公民的节水意识,合理利用水资源,某市采取了价格调控措施,该市自来水收费价格见价目表.若某户居民1月份用水8吨,则应缴水费:2×6+4×(8-6)=20(元).
(1)若该户居民2月份用水12.5 吨,则应缴水费多少元
(2)若该户居民3、4月份共用水15吨(4月份用水量超过3月份),共缴水费44元,则该户居民3、4月份各用水多少吨
类型7 确定优化方案问题
13. 某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
优惠一:非会员购物,所有商品价格可获九折优惠.
优惠二:交纳200元会费成为该超市的会员,所有商品价格可获八折优惠.
(1)若用x(单位:元)表示所购商品的总价格,请你用含x的式子分别表示两种优惠方案优惠后所花的钱数.
(2)当所购商品的总价格是多少元时,两种优惠方案优惠后所花的钱数相同
(3)若某人计划在该超市购买一台价格为2 700元的电脑,请分析选择哪种优惠方案更省钱.
参考答案
专项一 解一元一次方程
1.C 【解析】 A项,将方程3x-2=2x-1移项,得3x-2x=-1+2,故本选项错误;B项,将方程3-x=2-5(x-1)去括号,得3-x= 2-5x+5,故本选项错误;C项,方程=1可化为=1,整理得3x=6,故本选项正确;D项,方程x=系数化为1,得x=,故本选项错误.故选C.
2.【解析】 (1)去括号,得2x+5=3x-3,
移项,得2x-3x=-3-5,
合并同类项,得-x=-8,
系数化为1,得x=8.
(2)去括号,得3x+3-2x-4=2x+3,
移项,合并同类项,得-x=4,
系数化为1,得x=-4.
(3)去分母,得3(x-1)-(2x-3)=2(6-x),
去括号,得3x-3-2x+3=12-2x,
移项,合并同类项,得3x=12,
系数化为1,得x=4.
(4)方程整理,得,
去分母,得(8-90x)-6(13-30x)=4(50x+10),
去括号,得8-90x-78+180x=200x+40,
移项,得-90x+180x-200x=40-8+78,
合并同类项,得-110x=110,
系数化为1,得x=-1.
3.【解析】 (1)① 去分母时,分子5x+2忘记加括号
(2)正确的解答过程如下:
去分母,得2(x-1)-(5x+2)=4,
去括号,得2x-2-5x-2=4,
移项,得2x-5x=4+2+2,
合并同类项,得-3x=8,
系数化为1,得x=-.
专项二 一元一次方程的实际应用
1.B
2.(240-150)x=150×12
3.A
4.【解析】 设C处的数为x,
根据题意,列方程得x+6+x+x-6+x-12=68,
解得x=20.
答:C处的数为20.
5.【解析】 设小亮原计划购买文具袋x个,
依题意,得10x-10×0.85(x+1)=11,
解得x=13.
答:小亮原计划购买文具袋13个.
6.【解析】 (1)40 60%
设甲种商品每件的进价为x元,
由题意,得60-x=50%x,解得x=40,
所以甲种商品每件的进价为40元.
乙种商品每件的利润率为×100%=60%.
(2)设购进甲种商品y件,则购进乙种商品(50-y)件,
由题意,得40y+50(50-y)=2 100,解得y=40.
答:购进甲种商品40件.
7.C 【解析】 设瓶子的容积为V cm3,则V-10×(7-5)=10×4,解得V=60.故选C.
8.,或 【解析】 设开始注入x min的水量后,甲与乙的水位高度之差是0.5 cm.由题意分三种情况讨论:①当甲的水位高于乙的水位时,1-x=0.5,解得x=.②当乙的水位高于甲的水位,且甲的水位不变时,由x-1=0.5,解得x=.由题意可得向丙注水1 min,丙的水位上升 cm,因为=6>5,所以此时丙容器已向乙容器溢水,因为5÷(min),(cm),即经过 min丙容器的水位到达管子底部,乙的水位上升 cm,所以+2×(x-)-1=0.5,解得x=.③当乙的水位高于甲的水位,乙的水位到达管子底部,甲的水位上升时,因为乙的水位到达管子底部的时间为+(5-)÷÷2=(min),所以5-1-2×(x-)=0.5,解得x=.综上所述,开始注入,或 min的水量后,甲与乙的水位高度之差为0.5 cm.
9.【解析】 设这条公路的长为x km,
由题意,得,解得x=12.
答:这条公路的长为12 km.
10.【解析】 (1)根据题意,设甲、乙两队合作,需要x天完成,
则()x=1,解得x=6.
所以甲、乙两队合作,需要6天完成.
(2)设剩下部分由两队合作完成,还需要y天,
则×5+()y=1,解得y=3.
所以甲队先施工5天,剩下部分由两队合作完成,还需要3天.
11.【解析】 (1)设AB=10x km,则AD=BC=5x km,CD=2x km.
所以AD+DC+CB=12x km,
故外环公路总长和市区公路长的比为12x∶10x=6∶5.
(2)由(1)可知,市区公路的长为10x km,外环公路的总长为12x km.
由题意,得,
解得x=1,所以10x=10.
故市区公路的长为10 km.
12.【解析】 (1)由题意得,应缴水费为2×6+4×(10-6)+8×(12.5-10)=12+16+20=48(元).
(2)设该户居民3月用水x吨,则4月用水(15-x)吨,
①当0根据题意,得2x+6×2+4(15-x-6)=44,
解得x=2,与6<15-x≤10 矛盾,舍去.
②当010时,
根据题意,得2x+6×2+4×4+8×(15-x-10)=44,
解得x=4,符合题意.
③当6根据题意,得6×2×2+4(x-6)+4(15-x-6)=44无解.
综上,该户居民3月份用水4吨,4月份用水11吨.
13.【解析】 (1)由题意可得,优惠一的花费为0.9x元,
优惠二的花费为(200+0.8x)元.
(2)若两种优惠方案优惠后所花的钱数相同,则0.9x=200+0.8x,
解得x=2 000.
答:当所购商品的总价格是2 000元时,两种优惠方案优惠后所花的钱数相同.
(3)优惠一的花费为0.9×2 700=2 430(元),
优惠二的花费为200+0.8×2 700=2 360(元),
2 430>2 360,所以优惠二更省钱.
专项一 解一元一次方程
1. 下列方程变形正确的是 ( )
A.将方程3x-2=2x-1移项,得3x-2x=-1-2
B.将方程3-x=2-5(x-1)去括号,得3-x=2-5x-1
C.方程=1可化简为3x=6
D.将方程x=系数化为1,得x=-1
2. 解下列方程:
(1)2x+5=3(x-1);
(2)3(x+1)-2(x+2)=2x+3;
(3);
(4).
3.如图是小慧同学书写的解方程=1的过程,请你认真阅读并回答下列问题:
(1)同学们看了小慧的解答过程,都说她做错了,你认为小慧同学从第 步开始出错,错误原因是 .
(2)请你写出正确的解答过程.
专项二 一元一次方程的实际应用
类型1 数学文化问题
1. 我国古代名著《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有人共买物,人出八,盈三;人出七,不足四,问人数几何.原文意思是:现在有一些人共同买一个物品,每人出8元,还盈余3元;每人出7元,则还差4元,问共有多少人.如果假设共有x人,那么可列方程为 ( )
A.8x+3=7x+4 B.8x-3=7x+4
C.8x+3=7x-4 D.8x-3=7x-4
2. 我国古代数学著作《算学启蒙》中有这样一个数学问题,其大意是:跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马再从原地出发,几天可以追上慢马 设快马x天可以追上慢马,根据题意,可列方程为 .
类型2 月历问题
3. 如图,在某年1月份的月历表中,任意框出表中竖列上三个相邻的数,这三个数的和不可能是( )
日 一 二 三 四 五 六
1 2 3 4 5
6 7 8 9 10 11 12
13 14 15 16 17 18 19
20 21 22 23 24 25 26
27 28 29 30 31
A.21 B.45 C.66 D.72
4. 如图是2020年1月的月历,小明用长方形按图示方向从中任意框出4个数,若这四个数的和为68,则C处的数是多少
类型3 销售问题
5. 巴川学校初中2023级开展校园艺术节系列活动,校学生会代表小亮到文体超市购买若干个文具袋作为奖品.这种文具袋标价每个10元,请认真阅读结账时老板与小亮的对话,求小亮原计划购买文具袋多少个.
6. 某商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.
(1)甲种商品每件的进价为 元,乙种商品每件的利润率为 .
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2 100元,求购进甲种商品多少件.
类型4 等积变形问题
7. 一个密封的瓶子里装着一些水(如图所示),已知瓶子的底面积为10 cm2,请你根据图中标明的数据,计算瓶子的容积是 ( )
A.80 cm3 B.70 cm3 C.60 cm3 D.50 cm3
8. 实验室里,水平桌面上有甲、乙、丙三个圆柱形容器(容器足够高),底面半径之比为1∶2∶1,用两根相同的管子在容器的5 cm高度处连通(即管子底端离容器底5 cm),现三个容器中,只有甲中有水,且水位高1 cm,如图所示.若每分钟同时向乙和丙注入相同量的水,开始注水1 min,乙的水位上升 cm,则开始注入 min的水量后,甲与乙的水位高度之差是0.5 cm.
类型5 路程问题
9. 如图,折线AC—CB是一条公路的示意图,AC=8 km,甲骑摩托车从A地沿这条公路到B地,速度为40 km/h,乙骑自行车从C地到B地,速度为10 km/h,两人同时出发,结果甲比乙早到6分钟.求这条公路的长.
10. 为了治理污染,改善空气质量,现在广大农村正在实施“煤改气”工程.甲、乙两个工程队共同承接了某村“燃气壁挂炉注水”任务.若甲队单独施工,则需10天完成;若乙队单独施工,则需15天完成.
(1)若甲、乙两队合作,需要几天完成
(2)若甲队先施工5天,剩下部分由两队合作完成,还需要几天
11. 如图,某市A,B两地之间有两条公路,一条是市区公路AB,另一条是外环公路AD—DC—CB.这两条公路围成等腰梯形ABCD,其中DC∥AB,AB∶AD∶DC=10∶5∶2.
(1)求外环公路总长和市区公路长的比.
(2)某人驾车从A地出发,沿市区公路去B地,平均速度是40 km/h.返回时沿外环公路行驶,平均速度是80 km/h,结果比去时少用了 h,求市区公路的长.
类型6 计费问题
12. 为了加强公民的节水意识,合理利用水资源,某市采取了价格调控措施,该市自来水收费价格见价目表.若某户居民1月份用水8吨,则应缴水费:2×6+4×(8-6)=20(元).
(1)若该户居民2月份用水12.5 吨,则应缴水费多少元
(2)若该户居民3、4月份共用水15吨(4月份用水量超过3月份),共缴水费44元,则该户居民3、4月份各用水多少吨
类型7 确定优化方案问题
13. 某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
优惠一:非会员购物,所有商品价格可获九折优惠.
优惠二:交纳200元会费成为该超市的会员,所有商品价格可获八折优惠.
(1)若用x(单位:元)表示所购商品的总价格,请你用含x的式子分别表示两种优惠方案优惠后所花的钱数.
(2)当所购商品的总价格是多少元时,两种优惠方案优惠后所花的钱数相同
(3)若某人计划在该超市购买一台价格为2 700元的电脑,请分析选择哪种优惠方案更省钱.
参考答案
专项一 解一元一次方程
1.C 【解析】 A项,将方程3x-2=2x-1移项,得3x-2x=-1+2,故本选项错误;B项,将方程3-x=2-5(x-1)去括号,得3-x= 2-5x+5,故本选项错误;C项,方程=1可化为=1,整理得3x=6,故本选项正确;D项,方程x=系数化为1,得x=,故本选项错误.故选C.
2.【解析】 (1)去括号,得2x+5=3x-3,
移项,得2x-3x=-3-5,
合并同类项,得-x=-8,
系数化为1,得x=8.
(2)去括号,得3x+3-2x-4=2x+3,
移项,合并同类项,得-x=4,
系数化为1,得x=-4.
(3)去分母,得3(x-1)-(2x-3)=2(6-x),
去括号,得3x-3-2x+3=12-2x,
移项,合并同类项,得3x=12,
系数化为1,得x=4.
(4)方程整理,得,
去分母,得(8-90x)-6(13-30x)=4(50x+10),
去括号,得8-90x-78+180x=200x+40,
移项,得-90x+180x-200x=40-8+78,
合并同类项,得-110x=110,
系数化为1,得x=-1.
3.【解析】 (1)① 去分母时,分子5x+2忘记加括号
(2)正确的解答过程如下:
去分母,得2(x-1)-(5x+2)=4,
去括号,得2x-2-5x-2=4,
移项,得2x-5x=4+2+2,
合并同类项,得-3x=8,
系数化为1,得x=-.
专项二 一元一次方程的实际应用
1.B
2.(240-150)x=150×12
3.A
4.【解析】 设C处的数为x,
根据题意,列方程得x+6+x+x-6+x-12=68,
解得x=20.
答:C处的数为20.
5.【解析】 设小亮原计划购买文具袋x个,
依题意,得10x-10×0.85(x+1)=11,
解得x=13.
答:小亮原计划购买文具袋13个.
6.【解析】 (1)40 60%
设甲种商品每件的进价为x元,
由题意,得60-x=50%x,解得x=40,
所以甲种商品每件的进价为40元.
乙种商品每件的利润率为×100%=60%.
(2)设购进甲种商品y件,则购进乙种商品(50-y)件,
由题意,得40y+50(50-y)=2 100,解得y=40.
答:购进甲种商品40件.
7.C 【解析】 设瓶子的容积为V cm3,则V-10×(7-5)=10×4,解得V=60.故选C.
8.,或 【解析】 设开始注入x min的水量后,甲与乙的水位高度之差是0.5 cm.由题意分三种情况讨论:①当甲的水位高于乙的水位时,1-x=0.5,解得x=.②当乙的水位高于甲的水位,且甲的水位不变时,由x-1=0.5,解得x=.由题意可得向丙注水1 min,丙的水位上升 cm,因为=6>5,所以此时丙容器已向乙容器溢水,因为5÷(min),(cm),即经过 min丙容器的水位到达管子底部,乙的水位上升 cm,所以+2×(x-)-1=0.5,解得x=.③当乙的水位高于甲的水位,乙的水位到达管子底部,甲的水位上升时,因为乙的水位到达管子底部的时间为+(5-)÷÷2=(min),所以5-1-2×(x-)=0.5,解得x=.综上所述,开始注入,或 min的水量后,甲与乙的水位高度之差为0.5 cm.
9.【解析】 设这条公路的长为x km,
由题意,得,解得x=12.
答:这条公路的长为12 km.
10.【解析】 (1)根据题意,设甲、乙两队合作,需要x天完成,
则()x=1,解得x=6.
所以甲、乙两队合作,需要6天完成.
(2)设剩下部分由两队合作完成,还需要y天,
则×5+()y=1,解得y=3.
所以甲队先施工5天,剩下部分由两队合作完成,还需要3天.
11.【解析】 (1)设AB=10x km,则AD=BC=5x km,CD=2x km.
所以AD+DC+CB=12x km,
故外环公路总长和市区公路长的比为12x∶10x=6∶5.
(2)由(1)可知,市区公路的长为10x km,外环公路的总长为12x km.
由题意,得,
解得x=1,所以10x=10.
故市区公路的长为10 km.
12.【解析】 (1)由题意得,应缴水费为2×6+4×(10-6)+8×(12.5-10)=12+16+20=48(元).
(2)设该户居民3月用水x吨,则4月用水(15-x)吨,
①当0
解得x=2,与6<15-x≤10 矛盾,舍去.
②当0
根据题意,得2x+6×2+4×4+8×(15-x-10)=44,
解得x=4,符合题意.
③当6
综上,该户居民3月份用水4吨,4月份用水11吨.
13.【解析】 (1)由题意可得,优惠一的花费为0.9x元,
优惠二的花费为(200+0.8x)元.
(2)若两种优惠方案优惠后所花的钱数相同,则0.9x=200+0.8x,
解得x=2 000.
答:当所购商品的总价格是2 000元时,两种优惠方案优惠后所花的钱数相同.
(3)优惠一的花费为0.9×2 700=2 430(元),
优惠二的花费为200+0.8×2 700=2 360(元),
2 430>2 360,所以优惠二更省钱.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
