第四章 图形的相似 单元检测题(无答案) 2023—2024学年北师大版数学九年级上册
文档属性
| 名称 | 第四章 图形的相似 单元检测题(无答案) 2023—2024学年北师大版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 15:13:56 | ||
图片预览


文档简介
九年级数学学力检测(二)
(九上第四章 图形的相似)
学校 班级 姓名
说明:全卷分A卷和B卷,A卷100分,B卷50分,满分150分;检测时间120分钟.
A卷(100分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1.已知,下列变形错误的是( )
A. B. C. D.
2.如图所示,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C等于( )
A.40° B.60°
C.80° D.100°
3.下列命题中,是真命题的是( )
A.等腰三角形都相似 B.等边三角形都相似
C.锐角三角形都相似 D.直角三角形都相似
4.在△ABC中,DE∥BC交AB于D,交AC于E,AD=5,BD=10,AE=3.则CE的值为( )
A.9 B.6 C.3 D.4
5.丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥正在建造中,在比例尺为1:500的图纸上,大桥的长度约为1.04米,则大桥的实际长度约是( )
A.104米 B.1040米 C.5200米 D.520米
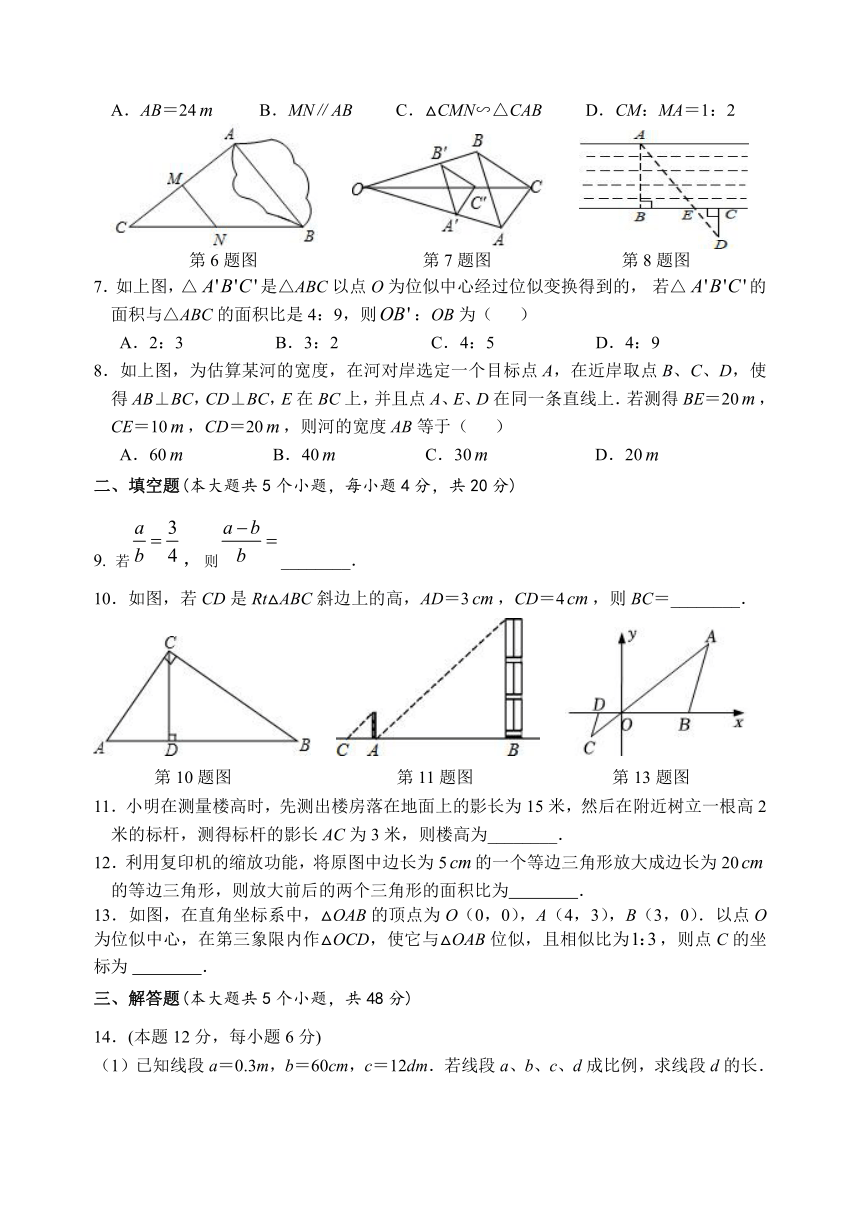
6.如下图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24 B.MN∥AB C.△CMN∽△CAB D.CM:MA=1:2
第6题图 第7题图 第8题图
7.如上图,△是△ABC以点O为位似中心经过位似变换得到的, 若△的
面积与△ABC的面积比是4:9,则:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
8.如上图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B、C、D,使得AB⊥BC,CD⊥BC,E在BC上,并且点A、E、D在同一条直线上.若测得BE=20,CE=10,CD=20,则河的宽度AB等于( )
A.60 B.40 C.30 D.20
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 若,则________.
10.如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=________.
第10题图 第11题图 第13题图
11.小明在测量楼高时,先测出楼房落在地面上的影长为15米,然后在附近树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为________.
12.利用复印机的缩放功能,将原图中边长为5的一个等边三角形放大成边长为20
的等边三角形,则放大前后的两个三角形的面积比为 .
13.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作△OCD,使它与△OAB位似,且相似比为,则点C的坐标为 .
三、解答题(本大题共5个小题,共48分)
14.(本题12分,每小题6分)
(1)已知线段a=0.3m,b=60cm,c=12dm.若线段a、b、c、d成比例,求线段d的长.
(2)若,且,求的值;
15.(本题8分)如图,D、E分别是△ABC的边AB、BC上的点, 且.
求证:DE∥AC.
16.(本题8分)如图,□ABCD中,AE:EB=2:3,DE交AC于F.若△CDF的面积为20,求△AEF的面积.
17.(本题10分) 如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)若设CD=t,梯形COEB的面积为S,
当t为多少时,S的值最大?最大值是多少?
18.(本题10分) 如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.已知DE=.
(1)求证:DB=DM;
(2)直接写出线段DE的取值范围;
(3)若(),求线段MN的长.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为36,则较大多边形的周长为________.
20.已知:,则直线一定经过的象限是 .
21.如下图所示,△ABC中,PQ∥BC,若,,则______.
第23题图 第24题图 第25题图
22.如上图所示,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH值为________.
23.如上图所示,直角三角形ABC中,∠C=90°,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为___ __.
二、解答题(本大题共3个小题,共30分)
24.(本题8分) 如图所示.已知△ABC的边BC长120米,高AD长80米.某学校计划
将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图),其中EFGH的一边EF
在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平
方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建
爱心鱼池,每平方米投资4元.
(1)当FG长为多少米时,种草的面积与
种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,
△ABC空地改造总投资最小?
25.(本题10分) 如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1/s,点Q运动的速度是2/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为(s).
(1)当=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(),求S与的关系式;
(3)作QR∥BA交AC于点R,连接PR,当为多少
时,△APR∽△PRQ?
26.(本题12分) 如图,将矩形OABC放置在平面直角坐标系中,点D在边OC上,点E在边OA上,把矩形沿直线DE翻折,使点O落在边AB上的点F处,且.
若线段OA的长是一元二次方程的一个根,又2AB=3AO.
(1)求点B、F的坐标;
(2)求直线ED的解析式;
(3)在直线ED、FD上是否存在点M、N,使
以点C、D、M、N为顶点的四边形是平行四
边形?若存在,请直接写出点M的坐标;若
不存在,请说明理由.
(九上第四章 图形的相似)
学校 班级 姓名
说明:全卷分A卷和B卷,A卷100分,B卷50分,满分150分;检测时间120分钟.
A卷(100分)
一、选择题(本大题共8个小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求)
1.已知,下列变形错误的是( )
A. B. C. D.
2.如图所示,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C等于( )
A.40° B.60°
C.80° D.100°
3.下列命题中,是真命题的是( )
A.等腰三角形都相似 B.等边三角形都相似
C.锐角三角形都相似 D.直角三角形都相似
4.在△ABC中,DE∥BC交AB于D,交AC于E,AD=5,BD=10,AE=3.则CE的值为( )
A.9 B.6 C.3 D.4
5.丽水市第一座横跨瓯江的单塔斜拉式大桥紫金大桥正在建造中,在比例尺为1:500的图纸上,大桥的长度约为1.04米,则大桥的实际长度约是( )
A.104米 B.1040米 C.5200米 D.520米
6.如下图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )
A.AB=24 B.MN∥AB C.△CMN∽△CAB D.CM:MA=1:2
第6题图 第7题图 第8题图
7.如上图,△是△ABC以点O为位似中心经过位似变换得到的, 若△的
面积与△ABC的面积比是4:9,则:OB为( )
A.2:3 B.3:2 C.4:5 D.4:9
8.如上图,为估算某河的宽度,在河对岸选定一个目标点A,在近岸取点B、C、D,使得AB⊥BC,CD⊥BC,E在BC上,并且点A、E、D在同一条直线上.若测得BE=20,CE=10,CD=20,则河的宽度AB等于( )
A.60 B.40 C.30 D.20
二、填空题(本大题共5个小题,每小题4分,共20分)
9. 若,则________.
10.如图,若CD是Rt△ABC斜边上的高,AD=3,CD=4,则BC=________.
第10题图 第11题图 第13题图
11.小明在测量楼高时,先测出楼房落在地面上的影长为15米,然后在附近树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为________.
12.利用复印机的缩放功能,将原图中边长为5的一个等边三角形放大成边长为20
的等边三角形,则放大前后的两个三角形的面积比为 .
13.如图,在直角坐标系中,△OAB的顶点为O(0,0),A(4,3),B(3,0).以点O为位似中心,在第三象限内作△OCD,使它与△OAB位似,且相似比为,则点C的坐标为 .
三、解答题(本大题共5个小题,共48分)
14.(本题12分,每小题6分)
(1)已知线段a=0.3m,b=60cm,c=12dm.若线段a、b、c、d成比例,求线段d的长.
(2)若,且,求的值;
15.(本题8分)如图,D、E分别是△ABC的边AB、BC上的点, 且.
求证:DE∥AC.
16.(本题8分)如图,□ABCD中,AE:EB=2:3,DE交AC于F.若△CDF的面积为20,求△AEF的面积.
17.(本题10分) 如图,边长为4的正方形OABC的顶点O为坐标原点,点A在x轴的正半轴上,点C在y轴的正半轴上.动点D在线段BC上移动(不与B,C重合),连接OD,过点D作DE⊥OD,交边AB于点E,连接OE.
(1)当CD=1时,求点E的坐标;
(2)若设CD=t,梯形COEB的面积为S,
当t为多少时,S的值最大?最大值是多少?
18.(本题10分) 如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.已知DE=.
(1)求证:DB=DM;
(2)直接写出线段DE的取值范围;
(3)若(),求线段MN的长.
B卷(50分)
一、填空题(本大题共5个小题,每小题4分,共20分)
19.已知两个相似多边形的面积比是9:16,其中较小多边形的周长为36,则较大多边形的周长为________.
20.已知:,则直线一定经过的象限是 .
21.如下图所示,△ABC中,PQ∥BC,若,,则______.
第23题图 第24题图 第25题图
22.如上图所示,E,G,F,H分别是矩形ABCD四条边上的点,EF⊥GH,若AB=2,BC=3,则EF:GH值为________.
23.如上图所示,直角三角形ABC中,∠C=90°,AC=1,BC=2,P为斜边AB上一动点.PE⊥BC,PF⊥CA,则线段EF长的最小值为___ __.
二、解答题(本大题共3个小题,共30分)
24.(本题8分) 如图所示.已知△ABC的边BC长120米,高AD长80米.某学校计划
将它分割成△AHG、△BHE、△GFC和矩形EFGH四部分(如图),其中EFGH的一边EF
在边BC上.其余两个顶点H、G分别在边AB、AC上.现计划在△AHG上种草,每平
方米投资6元;在△BHE、△FCG上都种花,每平方米投资10元;在矩形EFGH上兴建
爱心鱼池,每平方米投资4元.
(1)当FG长为多少米时,种草的面积与
种花的面积相等?
(2)当矩形EFGH的边FG为多少米时,
△ABC空地改造总投资最小?
25.(本题10分) 如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1/s,点Q运动的速度是2/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为(s).
(1)当=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(),求S与的关系式;
(3)作QR∥BA交AC于点R,连接PR,当为多少
时,△APR∽△PRQ?
26.(本题12分) 如图,将矩形OABC放置在平面直角坐标系中,点D在边OC上,点E在边OA上,把矩形沿直线DE翻折,使点O落在边AB上的点F处,且.
若线段OA的长是一元二次方程的一个根,又2AB=3AO.
(1)求点B、F的坐标;
(2)求直线ED的解析式;
(3)在直线ED、FD上是否存在点M、N,使
以点C、D、M、N为顶点的四边形是平行四
边形?若存在,请直接写出点M的坐标;若
不存在,请说明理由.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
