人教A版(2019)选择性必修第一册 2.2.2直线的两点式方程 课件(共13张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 2.2.2直线的两点式方程 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 12:28:17 | ||
图片预览





文档简介
(共13张PPT)
高二数学 选择性必修 第一册
第二章 直线和圆的方程
2.2.2直线的两点式方程
1、点斜式:
2、斜截式:
3、适用条件:
复习回顾
过定点,斜率为,
过定点,斜率为,
斜率存在
1、掌握直线的两点式方程和截距式方程(数学抽象)
2、会选择适当的方程形式求直线方程(数学抽象)
3、能用直线的两点式方程和截距式方程解答有关问题(数学运算)
【高考链接】直线的方程是学习平面解析几何知识的基础,高考中主要考查对直线的方程的求解与应用。
学习目标
建筑工人在砌墙时,时常在两个墙角分别立一根标志杆,在两根标志杆之间拉一根绳,沿着这根绳就能砌出直的墙。在平面直角坐标系中,这条直线的方程如何用两点确定呢?
情景引入
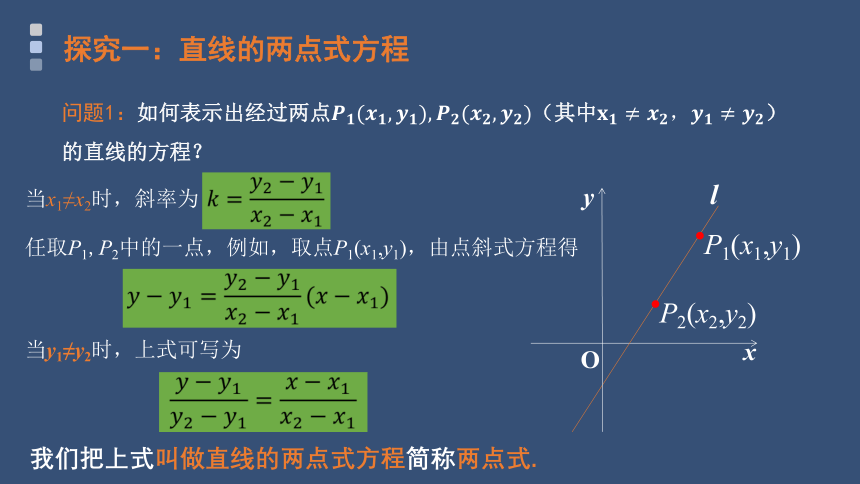
问题1:如何表示出经过两点(其中)的直线的方程?
探究一:直线的两点式方程
x
y
O
P1(x1,y1)
P2(x2,y2)
l
当x1≠x2时,斜率为
任取P1,P2中的一点,例如,取点P1(x1,y1),由点斜式方程得
当y1≠y2时,上式可写为
我们把上式叫做直线的两点式方程简称两点式.
探究新知:一、直线的两点式方程
l
x
y
O
P1(x1,y1)
P2(x2,y2)
1、两点式方程
x1≠x2或y1≠y2
【小结】垂直于坐标轴的直线不能用两点式方程。
2、适用条件:
①当x1=x2时,直线方程为
②当y1=y2时,直线方程为
例3 如图,已知直线l与x轴的交点A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程.
解:将两点A(a,0),B(0,b)的坐标代入两点式得:
即,
探究二:截距式方程
l
x
y
O
B
A
截距式方程
纵截距
横截距
1.定义
直线l在x轴的交点(a,0)的横坐标a叫做直线l在x轴上的截距(横截距)
直线l在y轴的交点(0,b)的纵坐标b叫做直线l在y轴上的截距(纵截距)
方程 叫做直线的截距式方程,简称截距式.
2.适用条件:与坐标轴有截距且a≠0,b≠0
当a=0,b=0时,直线l的方程为:y=kx
探究新知:二、截距式方程
l
x
y
O
B
A
【小结】过原点和垂直于坐标轴的直线不适用截距式方程。
例4 已知△ABC的三个顶点A(-5,0),B(3,-3),C(0,2),求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
教材例题
基础练习
x+5y-15=0
(一)一点和方向确定一条直线
1、点斜式
直线 l 经过点P0(x0,y0),斜率为k:y-y0=k(x-x0)
适用条件:斜率存在
2、斜截式
直线 l 经过点P0(0,b),斜率为k:y=kx+b
适用条件:斜率存在
当堂小结
(二)两点确定一条直线
1、两点式
直线 l 经过点P1(x1,y1),P2(x2,y2):
适用条件:直线不垂直于坐标轴
2、截距式
直线 l 经过点P1(a,0),P2(0,b):
适用条件:直线不经过原点和垂直于坐标轴
思维拓展
B
高二数学 选择性必修 第一册
第二章 直线和圆的方程
2.2.2直线的两点式方程
1、点斜式:
2、斜截式:
3、适用条件:
复习回顾
过定点,斜率为,
过定点,斜率为,
斜率存在
1、掌握直线的两点式方程和截距式方程(数学抽象)
2、会选择适当的方程形式求直线方程(数学抽象)
3、能用直线的两点式方程和截距式方程解答有关问题(数学运算)
【高考链接】直线的方程是学习平面解析几何知识的基础,高考中主要考查对直线的方程的求解与应用。
学习目标
建筑工人在砌墙时,时常在两个墙角分别立一根标志杆,在两根标志杆之间拉一根绳,沿着这根绳就能砌出直的墙。在平面直角坐标系中,这条直线的方程如何用两点确定呢?
情景引入
问题1:如何表示出经过两点(其中)的直线的方程?
探究一:直线的两点式方程
x
y
O
P1(x1,y1)
P2(x2,y2)
l
当x1≠x2时,斜率为
任取P1,P2中的一点,例如,取点P1(x1,y1),由点斜式方程得
当y1≠y2时,上式可写为
我们把上式叫做直线的两点式方程简称两点式.
探究新知:一、直线的两点式方程
l
x
y
O
P1(x1,y1)
P2(x2,y2)
1、两点式方程
x1≠x2或y1≠y2
【小结】垂直于坐标轴的直线不能用两点式方程。
2、适用条件:
①当x1=x2时,直线方程为
②当y1=y2时,直线方程为
例3 如图,已知直线l与x轴的交点A(a,0),与y轴的交点为B(0,b),其中a≠0,b≠0,求直线l的方程.
解:将两点A(a,0),B(0,b)的坐标代入两点式得:
即,
探究二:截距式方程
l
x
y
O
B
A
截距式方程
纵截距
横截距
1.定义
直线l在x轴的交点(a,0)的横坐标a叫做直线l在x轴上的截距(横截距)
直线l在y轴的交点(0,b)的纵坐标b叫做直线l在y轴上的截距(纵截距)
方程 叫做直线的截距式方程,简称截距式.
2.适用条件:与坐标轴有截距且a≠0,b≠0
当a=0,b=0时,直线l的方程为:y=kx
探究新知:二、截距式方程
l
x
y
O
B
A
【小结】过原点和垂直于坐标轴的直线不适用截距式方程。
例4 已知△ABC的三个顶点A(-5,0),B(3,-3),C(0,2),求边BC所在直线的方程,以及这条边上的中线AM所在直线的方程.
教材例题
基础练习
x+5y-15=0
(一)一点和方向确定一条直线
1、点斜式
直线 l 经过点P0(x0,y0),斜率为k:y-y0=k(x-x0)
适用条件:斜率存在
2、斜截式
直线 l 经过点P0(0,b),斜率为k:y=kx+b
适用条件:斜率存在
当堂小结
(二)两点确定一条直线
1、两点式
直线 l 经过点P1(x1,y1),P2(x2,y2):
适用条件:直线不垂直于坐标轴
2、截距式
直线 l 经过点P1(a,0),P2(0,b):
适用条件:直线不经过原点和垂直于坐标轴
思维拓展
B
