北师大版六下第一单元 圆柱体积的应用课件(共16张PPT)
文档属性
| 名称 | 北师大版六下第一单元 圆柱体积的应用课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 38.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
圆 柱 体 积 的 应 用
(北师大版六下第一单元“圆柱的体积”拓展与提升)
旧知梳理
01
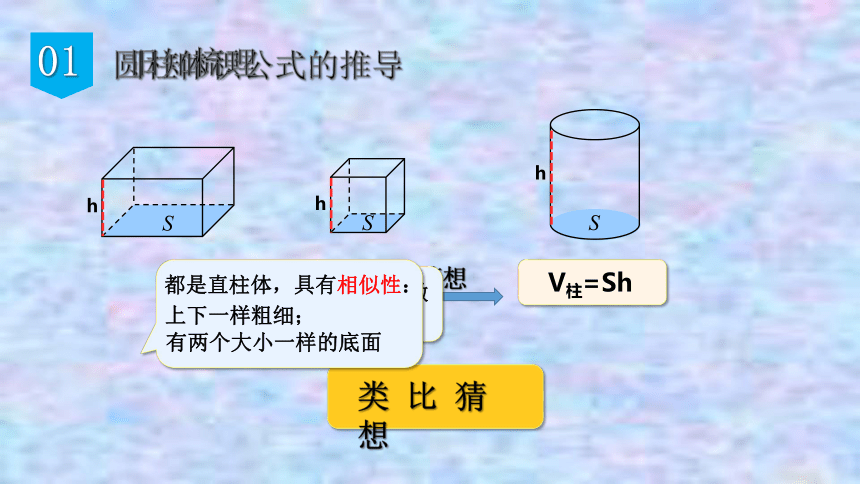
圆柱体积公式的推导
h
h
h
猜想
物体所占空间的大小叫做物体的体积。
类 比 猜 想
V长=Sh
V柱=Sh
旧知梳理
都是直柱体,具有相似性:
上下一样粗细;
有两个大小一样的底面
01
底面积
底面积
高
高
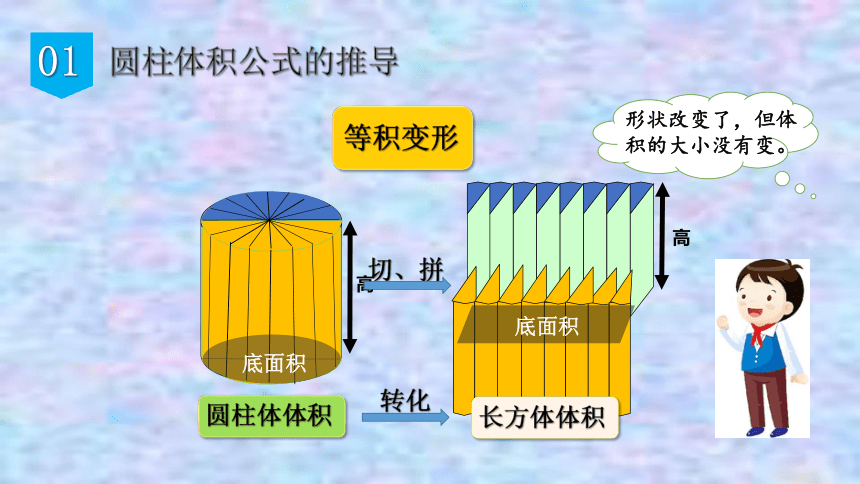
圆柱体积公式的推导
切、拼
转化
形状改变了,但体积的大小没有变。
圆柱体体积
长方体体积
等积变形
01
圆柱体积公式的推导
…
推导
01
猜 想
验 证
归纳总结
转化法
V柱=S h
=π r ×h
解决问题
02
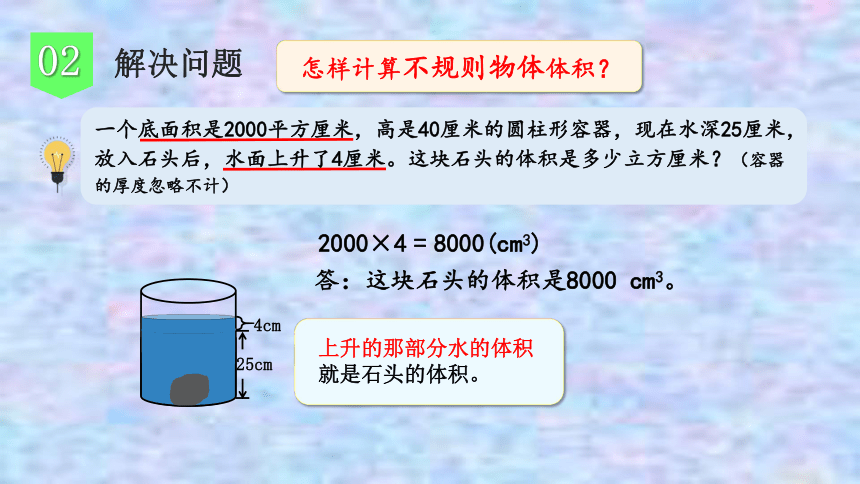
25cm
4cm
2000×4 = 8000(cm3)
答:这块石头的体积是8000 cm3。
解决问题
上升的那部分水的体积
就是石头的体积。
一个底面积是2000平方厘米,高是40厘米的圆柱形容器,现在水深25厘米,放入石头后,水面上升了4厘米。这块石头的体积是多少立方厘米?(容器的厚度忽略不计)
怎样计算不规则物体体积?
02
17cm
5cm
瓶子的容积相当于:底面积不变,
高是(17+5)cm的圆柱的体积。
饮料的容积340毫升
相当于瓶子容积的 17
17+5
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
转化成规则的圆柱进行计算。
空余部分的体积也相等,
不管是正放或是倒放,
瓶子里面饮料的体积一定。
瓶子的形状不规则,无法直接进行计算
解决问题
可以
02
5cm
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
解决问题
02
先求出高为1cm的圆柱的容积。
17cm
17cm
5cm
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
解决问题
02
梳理总结
03
方法①
方法②
方法③
方法④
梳理总结
解决求圆柱形容器容积问题的关键是什么?
注意审题时找出题目中
隐藏的条件。
明确:瓶子正放或倒放时,饮料体积不变;
运用“转化法”将不规则物体体积转化成我们学过的规则立体图形来解决。
空余部分的容积也相
等,既是隐藏的条件,也是解答此题的关键。
03
策略一:
将新知转化成旧知识
策略二:
将不规则的转化成规则的
将复杂的转化成简单的
策略三:
策略四:
将抽象的转化成具体的
梳理总结
巧妙利用转化思维策略:
根据题目中存在的相等关系,通过换角度、换方式等办法……
03
……
拓展练习
04
拓展延伸
一个瓶子的瓶身呈圆柱形(不包括瓶颈),它的底面直径是10cm,高是30cm,瓶子里装有15cm高的水,把瓶盖拧紧后倒放,水深25cm(如图),这个瓶子的容积是多少?(瓶子的厚度忽略不计)
04
30cm
15cm
10cm
25cm
感
谢
聆
听
圆 柱 体 积 的 应 用
(北师大版六下第一单元“圆柱的体积”拓展与提升)
旧知梳理
01
圆柱体积公式的推导
h
h
h
猜想
物体所占空间的大小叫做物体的体积。
类 比 猜 想
V长=Sh
V柱=Sh
旧知梳理
都是直柱体,具有相似性:
上下一样粗细;
有两个大小一样的底面
01
底面积
底面积
高
高
圆柱体积公式的推导
切、拼
转化
形状改变了,但体积的大小没有变。
圆柱体体积
长方体体积
等积变形
01
圆柱体积公式的推导
…
推导
01
猜 想
验 证
归纳总结
转化法
V柱=S h
=π r ×h
解决问题
02
25cm
4cm
2000×4 = 8000(cm3)
答:这块石头的体积是8000 cm3。
解决问题
上升的那部分水的体积
就是石头的体积。
一个底面积是2000平方厘米,高是40厘米的圆柱形容器,现在水深25厘米,放入石头后,水面上升了4厘米。这块石头的体积是多少立方厘米?(容器的厚度忽略不计)
怎样计算不规则物体体积?
02
17cm
5cm
瓶子的容积相当于:底面积不变,
高是(17+5)cm的圆柱的体积。
饮料的容积340毫升
相当于瓶子容积的 17
17+5
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
转化成规则的圆柱进行计算。
空余部分的体积也相等,
不管是正放或是倒放,
瓶子里面饮料的体积一定。
瓶子的形状不规则,无法直接进行计算
解决问题
可以
02
5cm
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
解决问题
02
先求出高为1cm的圆柱的容积。
17cm
17cm
5cm
有一种饮料的瓶身呈圆柱形(不包括瓶颈),瓶内装有340毫升饮料,正放时瓶内饮料高度为17厘米,倒放时瓶内空余部分高5厘米(如图所示),这个瓶子的容积是多少?
解决问题
02
梳理总结
03
方法①
方法②
方法③
方法④
梳理总结
解决求圆柱形容器容积问题的关键是什么?
注意审题时找出题目中
隐藏的条件。
明确:瓶子正放或倒放时,饮料体积不变;
运用“转化法”将不规则物体体积转化成我们学过的规则立体图形来解决。
空余部分的容积也相
等,既是隐藏的条件,也是解答此题的关键。
03
策略一:
将新知转化成旧知识
策略二:
将不规则的转化成规则的
将复杂的转化成简单的
策略三:
策略四:
将抽象的转化成具体的
梳理总结
巧妙利用转化思维策略:
根据题目中存在的相等关系,通过换角度、换方式等办法……
03
……
拓展练习
04
拓展延伸
一个瓶子的瓶身呈圆柱形(不包括瓶颈),它的底面直径是10cm,高是30cm,瓶子里装有15cm高的水,把瓶盖拧紧后倒放,水深25cm(如图),这个瓶子的容积是多少?(瓶子的厚度忽略不计)
04
30cm
15cm
10cm
25cm
感
谢
聆
听
