九年级数学课堂教学诊断练习(一)一元二次方程(pdf、含答案)
文档属性
| 名称 | 九年级数学课堂教学诊断练习(一)一元二次方程(pdf、含答案) |  | |
| 格式 | |||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 14:34:16 | ||
图片预览

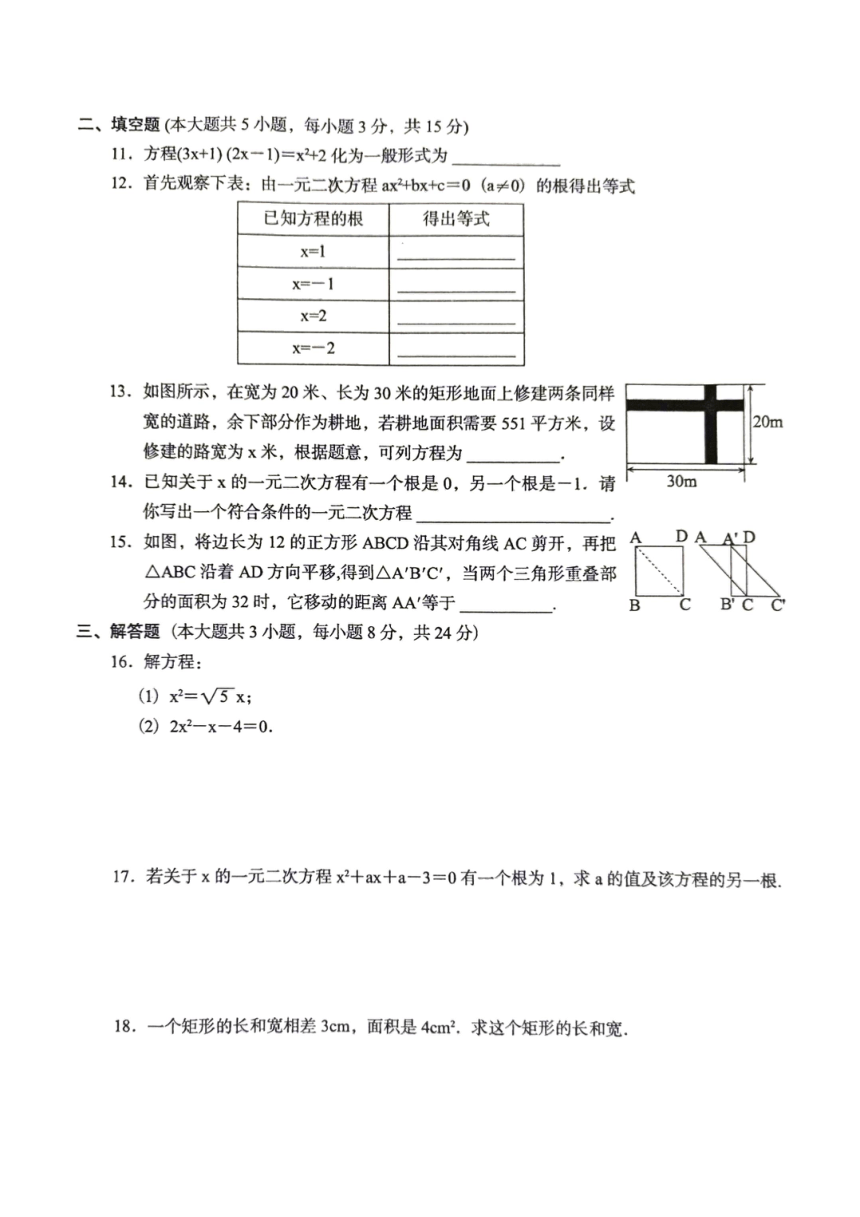


文档简介
2023—2024 学年度第一学期
九年级数学课堂教学诊断练习参考答案
(一)
1.C 2.B 3.D 4.A 5.A 6.A 7.C 8.A 9.A 10.A
11.5x2﹣x﹣3=0 12. a+b+ c = 0 a b+c = 0 4a+ 2b+ c = 0 4a 2b+ c = 0
13. (30 x)(20 x) = 551 14. x2 + x = 0 15.4 或 8
【分析】由平移的性质可知阴影部分为平行四边形,设 A′D=x,根据题意阴影部分的面积
为(12 x)×x,即 x(12 x),当 x(12 x)=32 时,解得:x=4 或 x=8,所以 AA′=8 或 AA′=4.
【详解】设 AA′=x,AC 与 A′B′相交于点 E,
∵△ACD 是正方形 ABCD 剪开得到的,
∴△ACD 是等腰直角三角形,
∴∠A=45 ,
∴△AA′E 是等腰直角三角形,
∴A′E=AA′=x,
A′D=AD AA′=12 x,
∵两个三角形重叠部分的面积为 32,
∴x(12 x)=32,
整理得,x 2 12x+32=0,
解得 x 1 =4,x 2 =8,
即移动的距离 AA′等 4 或 8.
【点睛】本题考查正方形和图形的平移,熟练掌握计算法则是解题关键·.
16.(1)解:∵ x2 = 5x ,
∴ x2 5x = 0,
∴ x (x 5) = 0,
解得 x1 = 0,x2 = 5 ;
(2)解:∵2x2 x 4 = 0,
∴a = 2,b = 1,c = 4,
2 2∴ =b 4ac = ( 1) 4 2 ( 4) = 33 0,
b b2 4ac 1 33
∴ x = = ,
2a 4
1+ 33 1 33
解得 x = ,x = . 1 2
4 4
17.解:将 x =1代入方程 x2 + ax+ a 3= 0,得1+a+ a 3= 0,
解得a =1,
∴原方程为 x2 + x 2 = 0,即 (x + 2)(x 1) = 0 ,
解得 x =1或 x = 2
∴方程的另一根为 2.
18.解:设矩形的宽为 x cm,则长为( x+3) cm
由矩形面积公式可知 x(x+3) = 4,
整理得 x2 +3x 4 = 0,
解得 x1 = 4 , x2 =1.
因为矩形的边长不能是负数,所以 x = 4不符合题意,舍去,
所以 x =1.
所以 x+3=1+3= 4.
答:这个矩形的长为 4 cm,宽为 1cm .
19.(1)解: AB的长为 x 米,且篱笆的总长度为30米,
BC 的长为 (30 3x)米.
花圃的面积 y = x (30 3x) = 3x2 +30x ,
∵墙的长度为10m,
30 3x 0
∴ ,
30 3x 10
20
x 10,
3
20
∴ y = 3x
2 + 30x x 10 ;
3
(2)解:依题意得: x (30 3x) = 63,
整理得: x2 10x + 21= 0 ,
解得: x1 = 3(不符合题意,舍去), x2 = 7.
答: AB 的长是 7 米.
20.(1)由于 x|a| 1 x 2 = 0是关于 x 的一元二次方程,
所以 | a | 1= 2 ,
解得a = 3;
(2)由(1)知,该方程为 x2 x 2 = 0,
把 x =m代入,得m2 m 2 = 0,
所以m2 m = 2 ,①
2
由m2 m 2 = 0,得m 1 = 0,
m
2
所以m =1,②
m
2 2
把①和②代入 (m m) m +1 ,
m
2
得 (m2 m) m +1 = 2 (1+1) = 4 ,
m
( 2 )
2
即 m m m +1 = 4.
m
21.解:(1)零售单价每降低 0.1 元,每天可多卖出 100 只粽子,
则降低 m 元,每天多卖出 1000m 只粽子,每只利润为(1- m)元,
∴每天可卖出(1000m + 300)只粽子,每天获得的利润为(1- m)(1000m+300)
故答案为:(1000m+300),(1- m)(1000m+300)
(2)根据题意得,(1- m)(1000m+300) = 420,
解得 m1= 0.4,m2= 0.3
因为要使卖出的粽子更多,故取 m= 0.4
答:m 定为 0.4 时,才能使该店每天获取的利润是 420 元,并且卖出的粽子更多.
22. (1)∵△=m2﹣4(m﹣2)=(m﹣2)2+4>0,
∴无论 m 取任何实数,此方程总有两个不相等的实数根.
(2)∵ x2+mx+m﹣2=0 的两个实数根为 x1、x2,
∴x1+x2=﹣m,x1x2=m﹣2,
∴y=x 21 +x 22 +4x1x2=(x 21+x2) +2x1x2=(﹣m)2+2(m﹣2)=m2+2m﹣4;
(3)∵y=m2+2m﹣4=(m+1)2﹣5,
∴顶点(﹣1,﹣5),
又∵﹣1≤m≤2,∴当 x=﹣1 时,y 最小值=﹣5,
当 x=2 时,y 最大值=4,
∴﹣5≤y≤4.
23.解:设 xs 后,BP=AB-AP=(5-x)cm,BQ=2xcm.
(1)根据三角形的面积公式列方程,得
x(5-x)=4.
解得 x1=1,x2=4.
当 x=4 时 BQ=4×2=8 cm>7cm,不合题意,舍去.
所以 1s 后,△PBQ 的面积等于 4cm2.
(2)△PBQ 的面积不能等于 8cm2.
理由:根据三角形的面积公式列方程,得
x(5-x)=8.
整理,得 x2-5x+8=0.
因为 Δ=(-5)2-4×1×8=-7<0,
所以△PBQ 的面积不能等于 8 cm2.
(3)根据勾股定理列方程,得
(5-x)2+(2x)2=25.
解得 x1=2,x2=0(不符合题意,舍去).
所以 2s 后,PQ 的长度等于 5 m.
九年级数学课堂教学诊断练习参考答案
(一)
1.C 2.B 3.D 4.A 5.A 6.A 7.C 8.A 9.A 10.A
11.5x2﹣x﹣3=0 12. a+b+ c = 0 a b+c = 0 4a+ 2b+ c = 0 4a 2b+ c = 0
13. (30 x)(20 x) = 551 14. x2 + x = 0 15.4 或 8
【分析】由平移的性质可知阴影部分为平行四边形,设 A′D=x,根据题意阴影部分的面积
为(12 x)×x,即 x(12 x),当 x(12 x)=32 时,解得:x=4 或 x=8,所以 AA′=8 或 AA′=4.
【详解】设 AA′=x,AC 与 A′B′相交于点 E,
∵△ACD 是正方形 ABCD 剪开得到的,
∴△ACD 是等腰直角三角形,
∴∠A=45 ,
∴△AA′E 是等腰直角三角形,
∴A′E=AA′=x,
A′D=AD AA′=12 x,
∵两个三角形重叠部分的面积为 32,
∴x(12 x)=32,
整理得,x 2 12x+32=0,
解得 x 1 =4,x 2 =8,
即移动的距离 AA′等 4 或 8.
【点睛】本题考查正方形和图形的平移,熟练掌握计算法则是解题关键·.
16.(1)解:∵ x2 = 5x ,
∴ x2 5x = 0,
∴ x (x 5) = 0,
解得 x1 = 0,x2 = 5 ;
(2)解:∵2x2 x 4 = 0,
∴a = 2,b = 1,c = 4,
2 2∴ =b 4ac = ( 1) 4 2 ( 4) = 33 0,
b b2 4ac 1 33
∴ x = = ,
2a 4
1+ 33 1 33
解得 x = ,x = . 1 2
4 4
17.解:将 x =1代入方程 x2 + ax+ a 3= 0,得1+a+ a 3= 0,
解得a =1,
∴原方程为 x2 + x 2 = 0,即 (x + 2)(x 1) = 0 ,
解得 x =1或 x = 2
∴方程的另一根为 2.
18.解:设矩形的宽为 x cm,则长为( x+3) cm
由矩形面积公式可知 x(x+3) = 4,
整理得 x2 +3x 4 = 0,
解得 x1 = 4 , x2 =1.
因为矩形的边长不能是负数,所以 x = 4不符合题意,舍去,
所以 x =1.
所以 x+3=1+3= 4.
答:这个矩形的长为 4 cm,宽为 1cm .
19.(1)解: AB的长为 x 米,且篱笆的总长度为30米,
BC 的长为 (30 3x)米.
花圃的面积 y = x (30 3x) = 3x2 +30x ,
∵墙的长度为10m,
30 3x 0
∴ ,
30 3x 10
20
x 10,
3
20
∴ y = 3x
2 + 30x x 10 ;
3
(2)解:依题意得: x (30 3x) = 63,
整理得: x2 10x + 21= 0 ,
解得: x1 = 3(不符合题意,舍去), x2 = 7.
答: AB 的长是 7 米.
20.(1)由于 x|a| 1 x 2 = 0是关于 x 的一元二次方程,
所以 | a | 1= 2 ,
解得a = 3;
(2)由(1)知,该方程为 x2 x 2 = 0,
把 x =m代入,得m2 m 2 = 0,
所以m2 m = 2 ,①
2
由m2 m 2 = 0,得m 1 = 0,
m
2
所以m =1,②
m
2 2
把①和②代入 (m m) m +1 ,
m
2
得 (m2 m) m +1 = 2 (1+1) = 4 ,
m
( 2 )
2
即 m m m +1 = 4.
m
21.解:(1)零售单价每降低 0.1 元,每天可多卖出 100 只粽子,
则降低 m 元,每天多卖出 1000m 只粽子,每只利润为(1- m)元,
∴每天可卖出(1000m + 300)只粽子,每天获得的利润为(1- m)(1000m+300)
故答案为:(1000m+300),(1- m)(1000m+300)
(2)根据题意得,(1- m)(1000m+300) = 420,
解得 m1= 0.4,m2= 0.3
因为要使卖出的粽子更多,故取 m= 0.4
答:m 定为 0.4 时,才能使该店每天获取的利润是 420 元,并且卖出的粽子更多.
22. (1)∵△=m2﹣4(m﹣2)=(m﹣2)2+4>0,
∴无论 m 取任何实数,此方程总有两个不相等的实数根.
(2)∵ x2+mx+m﹣2=0 的两个实数根为 x1、x2,
∴x1+x2=﹣m,x1x2=m﹣2,
∴y=x 21 +x 22 +4x1x2=(x 21+x2) +2x1x2=(﹣m)2+2(m﹣2)=m2+2m﹣4;
(3)∵y=m2+2m﹣4=(m+1)2﹣5,
∴顶点(﹣1,﹣5),
又∵﹣1≤m≤2,∴当 x=﹣1 时,y 最小值=﹣5,
当 x=2 时,y 最大值=4,
∴﹣5≤y≤4.
23.解:设 xs 后,BP=AB-AP=(5-x)cm,BQ=2xcm.
(1)根据三角形的面积公式列方程,得
x(5-x)=4.
解得 x1=1,x2=4.
当 x=4 时 BQ=4×2=8 cm>7cm,不合题意,舍去.
所以 1s 后,△PBQ 的面积等于 4cm2.
(2)△PBQ 的面积不能等于 8cm2.
理由:根据三角形的面积公式列方程,得
x(5-x)=8.
整理,得 x2-5x+8=0.
因为 Δ=(-5)2-4×1×8=-7<0,
所以△PBQ 的面积不能等于 8 cm2.
(3)根据勾股定理列方程,得
(5-x)2+(2x)2=25.
解得 x1=2,x2=0(不符合题意,舍去).
所以 2s 后,PQ 的长度等于 5 m.
同课章节目录
