3.1.2椭圆的简单几何性质(第二课时)(教学课件)(共30张PPT)
文档属性
| 名称 | 3.1.2椭圆的简单几何性质(第二课时)(教学课件)(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 14:34:26 | ||
图片预览











文档简介
(共30张PPT)
第 3 章圆锥曲线的方程
3.1.2椭圆的简单几何性质(第2课时)
1.进一步掌握椭圆的方程及其性质的应用,会判断直线与椭圆的位置关系.
2.能运用直线与椭圆的位置关系解决相关的弦长、中点弦问题.
学习目标
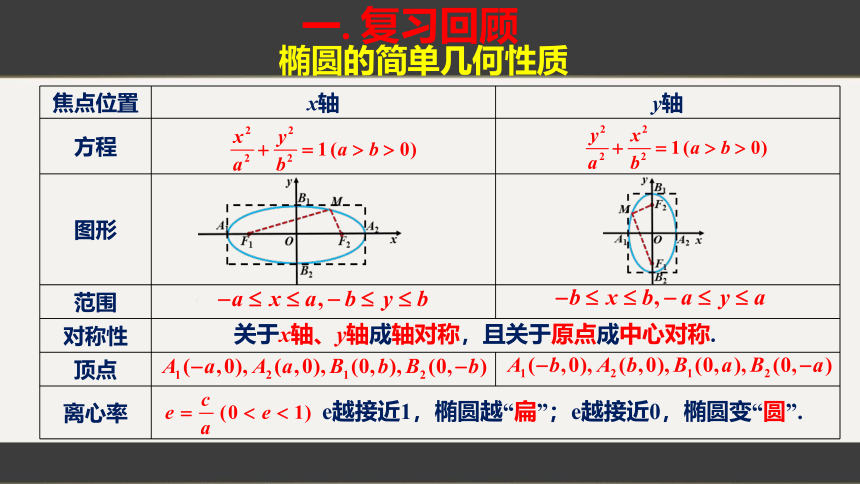
焦点位置 x轴 y轴
方程
图形
范围
对称性
顶点
离心率
关于x轴、y轴成轴对称,且关于原点成中心对称.
e越接近1,椭圆越“扁”;e越接近0,椭圆变“圆”.
一. 复习回顾
椭圆的简单几何性质
二.和椭圆有关的实际问题
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
例1. 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
二.和椭圆有关的实际问题
跟踪练习1(多选)嫦娥四号探测器,简称“四号星”,是世界首个在月球背面软着陆和巡视探测的航天器.2019年9月25日,中国科研人员利用嫦娥四号数据精确定位了嫦娥四号的着陆位置,并再现了嫦娥四号的落月过程,该成果由国际科学期刊《自然·通讯》在线发表.如图所示,现假设“四号星”沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,
用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,则下列式子正确的是
√
√
解析 由图可知,a1>a2,c1>c2所以a1+c1>a2+c2,所以A不正确;
在椭圆轨道Ⅰ中可得,a1-c1=|PF|,
在椭圆轨道Ⅱ中可得,|PF|=a2-c2,
所以a1-c1=a2-c2,所以B正确;
二.和椭圆有关的实际问题
三.椭圆的第二定义
所以点M的轨迹是长轴、短轴长分别为10,6的椭圆。
三.椭圆的第二定义
其中,定点F(c,0)是椭圆的焦点;
椭圆的第二定义:
三.椭圆的第二定义
焦准距
左、右准线
左、右焦点
上、下焦点
F(±c,0)
上、下准线
F(0,±c)
通径长
p=b2/c
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
要点梳理
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
求弦长的两种方法
(1)求出直线与椭圆的两交点坐标,用两点间距离公式求弦长.
(2)“联立—消元—列式”,利用弦长公式:
其中x1,x2(y1,y2)是上述一元二次方程的两根,由根与系数的关系求出两根之和与两根之积后代入公式可求得弦长.
提醒:如果直线方程涉及斜率,要注意斜率不存在的情况.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
解决椭圆中点弦问题的两种方法
(二)弦长及弦的中点问题
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
解法一:根与系数的关系、中点坐标公式法(“联立——消元——列式”)
设直线AB:y-1=k(x-2).A(x1,y1),B(x2,y2),得(4k2+1)x2-8(2k2-k)x+4(2k-1)2-16=0;
方法二 点差法:∵M(2,1)为线段AB的中点,∴x1+x2=4,y1+y2=2.作差得(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0.
方法三 对称点法(或共线法):设所求直线与椭圆的一个交点为A(x,y),由中点M(2,1),则B(4-x,2-y).∵A,B两点都在椭圆上,
相减得lAB: x+2y-4=0.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
(1)求椭圆E的方程;(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
(1)求椭圆E的方程;(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
(2)若存在点Q(m,0),使得∠PQM+∠PQN=180°,则直线QM和QN的斜率存在,分别设为k1,k2.等价于k1+k2=0.依题意,设直线l的方程为y=k(x-4).
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
设M(x1,y1),N(x2,y2),则
y1=k1(x1-4),y2=k2(x2-4),
当k≠0时,2x1x2-(m+4)(x1+x2)+8m=0,代入求得m=1,
当k=0时,也成立.所以存在点Q(1,0),使得∠PQM+∠PQN=180°.
2.若直线l:2x+by+3=0过椭圆C:10x2+y2=10的一个焦点,则b等于( )A.1 B.±1 C.-1 D.±2
五.当堂达标训练
B
C
B
4.已知椭圆的方程是x2+2y2-4=0,则以M(1,1)为中点的弦所在直线的方程是( )A.x+2y-3=0 B.2x+y-3=0 C.x-2y+3=0 D.2x-y+3=0
五.当堂达标训练
A
A
五.当堂达标训练
即x2-3x-8=0,则x1+x2=3,∴中点的坐标为
第 3 章圆锥曲线的方程
3.1.2椭圆的简单几何性质(第2课时)
1.进一步掌握椭圆的方程及其性质的应用,会判断直线与椭圆的位置关系.
2.能运用直线与椭圆的位置关系解决相关的弦长、中点弦问题.
学习目标
焦点位置 x轴 y轴
方程
图形
范围
对称性
顶点
离心率
关于x轴、y轴成轴对称,且关于原点成中心对称.
e越接近1,椭圆越“扁”;e越接近0,椭圆变“圆”.
一. 复习回顾
椭圆的简单几何性质
二.和椭圆有关的实际问题
解: 建立如图所示的平面直角坐标系, 设所求椭圆方程为
在Rt△BF1F2中,
由椭圆的性质知,
所以,所求的椭圆方程为
例1. 如图示, 一种电影放映灯的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分, 过对称轴的截口BAC是椭圆的一部分, 灯丝位于椭圆的一个焦点F1上, 片门位于另一个焦点F2上, 由椭圆一个焦点F1发出的光线, 经过旋转椭圆面反射后集中到另一个焦点F2 . 已知BC⊥F1F2 , |F1B|=2.8 cm, |F1F2|=4.5 cm. 试建 立适当的平面直角坐标系, 求截口BAC所在椭圆的方程(精确到0.1 cm).
二.和椭圆有关的实际问题
跟踪练习1(多选)嫦娥四号探测器,简称“四号星”,是世界首个在月球背面软着陆和巡视探测的航天器.2019年9月25日,中国科研人员利用嫦娥四号数据精确定位了嫦娥四号的着陆位置,并再现了嫦娥四号的落月过程,该成果由国际科学期刊《自然·通讯》在线发表.如图所示,现假设“四号星”沿地月转移轨道飞向月球后,在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行,之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行.若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距,
用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴长,则下列式子正确的是
√
√
解析 由图可知,a1>a2,c1>c2所以a1+c1>a2+c2,所以A不正确;
在椭圆轨道Ⅰ中可得,a1-c1=|PF|,
在椭圆轨道Ⅱ中可得,|PF|=a2-c2,
所以a1-c1=a2-c2,所以B正确;
二.和椭圆有关的实际问题
三.椭圆的第二定义
所以点M的轨迹是长轴、短轴长分别为10,6的椭圆。
三.椭圆的第二定义
其中,定点F(c,0)是椭圆的焦点;
椭圆的第二定义:
三.椭圆的第二定义
焦准距
左、右准线
左、右焦点
上、下焦点
F(±c,0)
上、下准线
F(0,±c)
通径长
p=b2/c
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
要点梳理
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(一)直线与椭圆位置关系及判定
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
求弦长的两种方法
(1)求出直线与椭圆的两交点坐标,用两点间距离公式求弦长.
(2)“联立—消元—列式”,利用弦长公式:
其中x1,x2(y1,y2)是上述一元二次方程的两根,由根与系数的关系求出两根之和与两根之积后代入公式可求得弦长.
提醒:如果直线方程涉及斜率,要注意斜率不存在的情况.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
解决椭圆中点弦问题的两种方法
(二)弦长及弦的中点问题
(1)根与系数的关系法:联立直线方程和椭圆方程构成方程组,消去一个未知数,利用一元二次方程根与系数的关系以及中点坐标公式解决.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
解法一:根与系数的关系、中点坐标公式法(“联立——消元——列式”)
设直线AB:y-1=k(x-2).A(x1,y1),B(x2,y2),得(4k2+1)x2-8(2k2-k)x+4(2k-1)2-16=0;
方法二 点差法:∵M(2,1)为线段AB的中点,∴x1+x2=4,y1+y2=2.作差得(x1+x2)(x1-x2)+4(y1+y2)(y1-y2)=0.
方法三 对称点法(或共线法):设所求直线与椭圆的一个交点为A(x,y),由中点M(2,1),则B(4-x,2-y).∵A,B两点都在椭圆上,
相减得lAB: x+2y-4=0.
四.直线与椭圆的位置关系
(二)弦长及弦的中点问题
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
(1)求椭圆E的方程;(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
(1)求椭圆E的方程;(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
(2)若存在点Q(m,0),使得∠PQM+∠PQN=180°,则直线QM和QN的斜率存在,分别设为k1,k2.等价于k1+k2=0.依题意,设直线l的方程为y=k(x-4).
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N.在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明理由.
四.直线与椭圆的位置关系
(三)与椭圆有关的综合问题
设M(x1,y1),N(x2,y2),则
y1=k1(x1-4),y2=k2(x2-4),
当k≠0时,2x1x2-(m+4)(x1+x2)+8m=0,代入求得m=1,
当k=0时,也成立.所以存在点Q(1,0),使得∠PQM+∠PQN=180°.
2.若直线l:2x+by+3=0过椭圆C:10x2+y2=10的一个焦点,则b等于( )A.1 B.±1 C.-1 D.±2
五.当堂达标训练
B
C
B
4.已知椭圆的方程是x2+2y2-4=0,则以M(1,1)为中点的弦所在直线的方程是( )A.x+2y-3=0 B.2x+y-3=0 C.x-2y+3=0 D.2x-y+3=0
五.当堂达标训练
A
A
五.当堂达标训练
即x2-3x-8=0,则x1+x2=3,∴中点的坐标为
