3.2.1双曲线及其标准方程(教学课件)(共25张PPT)
文档属性
| 名称 | 3.2.1双曲线及其标准方程(教学课件)(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 643.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第 3 章圆锥曲线的方程
3.2.1双曲线及其标准方程
1.掌握双曲线的标准方程及其求法.
2.会利用双曲线的定义和标准方程解决简单实际问题.
3.与椭圆的标准方程进行比较,并加以区分.
学习目标
1.椭圆的定义:
平面内与两个定点|F1F2|的距离的和等于常数(大于|F1F2| )的点的轨迹叫做椭圆.
2.椭圆的标准方程:
问题:如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
知识回顾
一.双曲线的定义
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
通常情况下,我们把|F1F2|记为2c(c>0), 常数记为2a(a>0),则双曲线定义还可以描述为
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
思考1 定义中为什么强调距离差的绝对值为常数?
一、双曲线的定义
如果不加绝对值,那得到的轨迹只是双曲线的一支.
一.双曲线的定义
新知探究
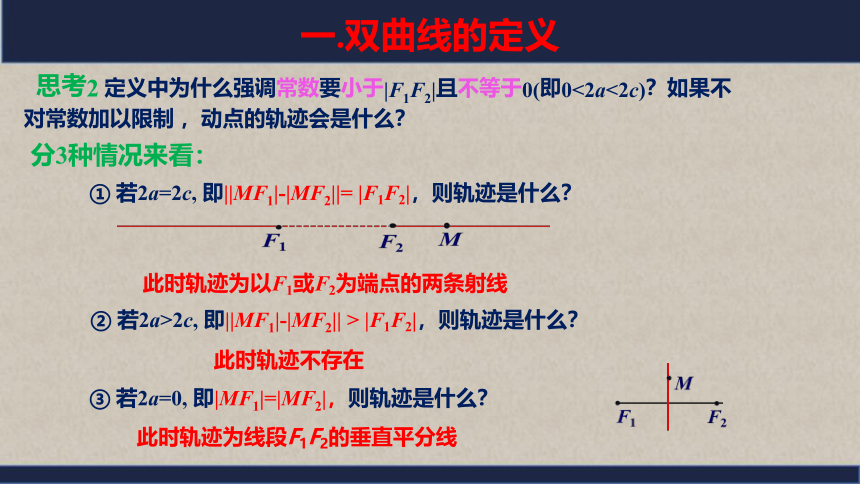
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2 定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
一.双曲线的定义
设M(x,y)为双曲线上任一点, 双曲线的焦距为2c(c>0), 那么焦点F1,F2的坐标分别为 F1(-c,0), F2(c,0), 又设||MF1|-|MF2||=2a(0二、双曲线标准方程
① 建系:
如图所示,建立平面直角坐标系.
② 设点:
③ 列式:
④ 化简整理得:
方程推导
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
二、双曲线标准方程
我们把上述方程叫做双曲线的标准方程,它表示焦点在x轴上,焦点坐标分别是F1(-c, 0), F2(c, 0)的双曲线,这里c2=a2+b2.
三.辨析和应用
1.平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
2.平面内到点F1(0,4),F2(0,-4)的距离之差等于6的点的轨迹是双曲线. ( )
3.平面内到点F1(0,4),F2(0,-4)的距离之差的绝对值等于8的点的轨迹是双曲线. ( )
4.在双曲线标准方程中,a,b,c之间的关系与椭圆中a,b,c之间的关系相同. ( )
概念辨析:
×
×
×
×
应用1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程.
三.辨析和应用
解:因为双曲线的焦点在x轴上,所以设它的标准方程为:
所以,双曲线的标准方程为:
由2c=10,2a=6,得c=5,a=3,所以b2=52-32=16.
应用2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s,
且声速为340m/s, 求炮弹爆炸点的轨迹方程.
三.辨析和应用
解:建立平面直角坐标系,使两点A,B在x轴 上,并且原点与线段AB的中点重合,
设炮弹炸点P的坐标为(x,y),则|PA|-|PB|=340×2=680,即2a=680,a=340
又|AB|=800,所以2c=800,c=400,b2=c2-a2=44400
因为|PA|-|PB|=680>0,所以点P的轨迹是双曲线的右支,因此x≥340,
所以,炮弹炸点的轨迹方程为:
想一想:如果A, B两处同时听到爆炸声,那么爆炸点应在什么样的曲线上?
答:爆炸点应在线段AB的中垂线上.
由应用2可知,利用两个不同的观测点测得同一炮弹爆炸声的时间差 , 就可以确定爆炸点所在的双曲线的方程,但是不能确定爆炸点的准确位置.
要想确定爆炸点的准确位置,还需增设一个观测点C,利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲线的一个重要应用 .
思考 如何准确测出爆炸点的位置?
三.辨析和应用
四.题型与方法
题型一 求双曲线的标准方程
把点A的坐标代入,得b2=9.
无解;
四.题型与方法
题型一 求双曲线的标准方程
(3)设双曲线的方程为Ax2+By2=1,AB<0.
因为点P,Q在双曲线上,解得
四.题型与方法
1.求双曲线标准方程的步骤
(1)定位:是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
(2)定量:是指确定a2,b2的数值,常由条件列方程组求解.
2.双曲线标准方程的两种求法
(1)定义法:根据双曲线的定义得到相应的a,b,c,再写出双曲线的标准方程.
提醒:若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
四.题型与方法
题型一 求双曲线的标准方程
四.题型与方法
题型二 双曲线中焦点三角形问题
(1)由双曲线的定义得||MF1|-|MF2||=2a=6,假设点M到另一个焦点的距离等于x,则|16-x|=6,解得x=10或x=22.故点M到另一个焦点的距离为10或22.
四.题型与方法
题型二 双曲线中焦点三角形问题
(2)将|PF2|-|PF1|=2a=6两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,则|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.在△F1PF2中,由余弦定理得
四.题型与方法
题型二 双曲线中焦点三角形问题
四.题型与方法
题型三 与双曲线有关的轨迹问题
解:以AB边所在的直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,如图所示,
(R为△ABC的外接圆半径).
∵2sin A+sin C=2sin B,∴2|BC|+|AB|=2|AC|,
由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点).
四.题型与方法
题型三 与双曲线有关的轨迹问题
求解双曲线的轨迹问题时要特别注意:(1)双曲线的焦点所在的坐标轴;(2)检验所求的轨迹对应的是双曲线的一支还是两支.
常见的方法:基本轨迹法
寻找几何关系,结合双曲线的定义,待定系数法得出对应的方程.
四.题型与方法
题型三 与双曲线有关的轨迹问题
[跟踪训练]3 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:x2+y2-10x+9=0,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
解:圆F1:(x+5)2+y2=1,圆心F1(-5,0),半径r1=1.圆F2:(x-5)2+y2=42,圆心F2(5,0),半径r2=4.设动圆M的半径为R,则有|MF1|=R+1,|MF2|=R+4,∴|MF2|-|MF1|=3<10=|F1F2|.∴点M的轨迹是以F1,F2为焦点的双曲线的左支,
双曲线两种标准方程的特点
① 方程用“-”号连接;
② 分母是a2, b2, 且a>0, b>0,但a, b大小不定;
③ c2=a2+b2 ;
④ 如果x2的系数是正的,则焦点在x轴上;
如果y2的系数是正的,则焦点在y轴上.
五.小结与练习
课堂小结
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a|MF1|+|MF2|=2a (a>c)
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
五.小结与练习
达标训练
五.小结与练习
1.动点P到点M(1,0)的距离与点N(3,0)的距离之差为2,则点P的轨迹是( )A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
2.已知F1(-8,3),F2(2,3),动点P满足|PF1|-|PF2|=10,则P点的轨迹是( )A.双曲线 B.双曲线的一支 C.直线 D.一条射线
D
D
D
五.小结与练习
C
C
A
8.已知双曲线方程为2x2-y2=k,焦距为6,则k的值为________.
9.已知F1,F2分别为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|等于________.
6或-6
4
五.小结与练习
第 3 章圆锥曲线的方程
3.2.1双曲线及其标准方程
1.掌握双曲线的标准方程及其求法.
2.会利用双曲线的定义和标准方程解决简单实际问题.
3.与椭圆的标准方程进行比较,并加以区分.
学习目标
1.椭圆的定义:
平面内与两个定点|F1F2|的距离的和等于常数(大于|F1F2| )的点的轨迹叫做椭圆.
2.椭圆的标准方程:
问题:如果把椭圆定义中“距离的和”改为“距离的差”那么动点的轨迹会发生怎样的变化?
知识回顾
一.双曲线的定义
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹叫做双曲线.
这两个定点叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
通常情况下,我们把|F1F2|记为2c(c>0), 常数记为2a(a>0),则双曲线定义还可以描述为
若||MF1|-|MF2||=2a<2c,则点M的轨迹是双曲线.
思考1 定义中为什么强调距离差的绝对值为常数?
一、双曲线的定义
如果不加绝对值,那得到的轨迹只是双曲线的一支.
一.双曲线的定义
新知探究
① 若2a=2c, 即||MF1|-|MF2||= |F1F2|,则轨迹是什么?
② 若2a>2c, 即||MF1|-|MF2|| > |F1F2|,则轨迹是什么?
③ 若2a=0, 即|MF1|=|MF2|,则轨迹是什么?
此时轨迹为以F1或F2为端点的两条射线
此时轨迹不存在
此时轨迹为线段F1F2的垂直平分线
分3种情况来看:
思考2 定义中为什么强调常数要小于|F1F2|且不等于0(即0<2a<2c)?如果不对常数加以限制 ,动点的轨迹会是什么?
一.双曲线的定义
设M(x,y)为双曲线上任一点, 双曲线的焦距为2c(c>0), 那么焦点F1,F2的坐标分别为 F1(-c,0), F2(c,0), 又设||MF1|-|MF2||=2a(0
① 建系:
如图所示,建立平面直角坐标系.
② 设点:
③ 列式:
④ 化简整理得:
方程推导
思考 类比椭圆,请思考焦点在y轴上的双曲线的标准方程是什么?
这个方程也是双曲线的标准方程,它表示焦点在y轴上,焦点坐标分别是F1(0, -c), F2(0, c)的双曲线,这里c2=a2+b2.
二、双曲线标准方程
我们把上述方程叫做双曲线的标准方程,它表示焦点在x轴上,焦点坐标分别是F1(-c, 0), F2(c, 0)的双曲线,这里c2=a2+b2.
三.辨析和应用
1.平面内到两定点的距离的差等于常数(小于两定点间距离)的点的轨迹是双曲线. ( )
2.平面内到点F1(0,4),F2(0,-4)的距离之差等于6的点的轨迹是双曲线. ( )
3.平面内到点F1(0,4),F2(0,-4)的距离之差的绝对值等于8的点的轨迹是双曲线. ( )
4.在双曲线标准方程中,a,b,c之间的关系与椭圆中a,b,c之间的关系相同. ( )
概念辨析:
×
×
×
×
应用1 已知双曲线的焦点 F1(-5, 0), F2(5, 0),双曲线上一点P到焦点的距离差的绝对值等于8,求双曲线的标准方程.
三.辨析和应用
解:因为双曲线的焦点在x轴上,所以设它的标准方程为:
所以,双曲线的标准方程为:
由2c=10,2a=6,得c=5,a=3,所以b2=52-32=16.
应用2 已知A, B两地相距800m, 在A地听到炮弹爆炸声比在B地晚2s,
且声速为340m/s, 求炮弹爆炸点的轨迹方程.
三.辨析和应用
解:建立平面直角坐标系,使两点A,B在x轴 上,并且原点与线段AB的中点重合,
设炮弹炸点P的坐标为(x,y),则|PA|-|PB|=340×2=680,即2a=680,a=340
又|AB|=800,所以2c=800,c=400,b2=c2-a2=44400
因为|PA|-|PB|=680>0,所以点P的轨迹是双曲线的右支,因此x≥340,
所以,炮弹炸点的轨迹方程为:
想一想:如果A, B两处同时听到爆炸声,那么爆炸点应在什么样的曲线上?
答:爆炸点应在线段AB的中垂线上.
由应用2可知,利用两个不同的观测点测得同一炮弹爆炸声的时间差 , 就可以确定爆炸点所在的双曲线的方程,但是不能确定爆炸点的准确位置.
要想确定爆炸点的准确位置,还需增设一个观测点C,利用A, C( 或B, C) 两处测得的爆炸声的时间差 , 求爆炸点所在的另一个双曲线的方程.
解这两个双曲线方程组成的方程组 , 就能确定爆炸点的准确位置 . 这是双曲线的一个重要应用 .
思考 如何准确测出爆炸点的位置?
三.辨析和应用
四.题型与方法
题型一 求双曲线的标准方程
把点A的坐标代入,得b2=9.
无解;
四.题型与方法
题型一 求双曲线的标准方程
(3)设双曲线的方程为Ax2+By2=1,AB<0.
因为点P,Q在双曲线上,解得
四.题型与方法
1.求双曲线标准方程的步骤
(1)定位:是指确定与坐标系的相对位置,在标准方程的前提下,确定焦点位于哪条坐标轴上,以确定方程的形式.
(2)定量:是指确定a2,b2的数值,常由条件列方程组求解.
2.双曲线标准方程的两种求法
(1)定义法:根据双曲线的定义得到相应的a,b,c,再写出双曲线的标准方程.
提醒:若焦点的位置不明确,应注意分类讨论,也可以设双曲线方程为mx2+ny2=1的形式,注意标明条件mn<0.
四.题型与方法
题型一 求双曲线的标准方程
四.题型与方法
题型二 双曲线中焦点三角形问题
(1)由双曲线的定义得||MF1|-|MF2||=2a=6,假设点M到另一个焦点的距离等于x,则|16-x|=6,解得x=10或x=22.故点M到另一个焦点的距离为10或22.
四.题型与方法
题型二 双曲线中焦点三角形问题
(2)将|PF2|-|PF1|=2a=6两边平方得|PF1|2+|PF2|2-2|PF1|·|PF2|=36,则|PF1|2+|PF2|2=36+2|PF1|·|PF2|=36+2×32=100.在△F1PF2中,由余弦定理得
四.题型与方法
题型二 双曲线中焦点三角形问题
四.题型与方法
题型三 与双曲线有关的轨迹问题
解:以AB边所在的直线为x轴,AB的垂直平分线为y轴,建立平面直角坐标系,如图所示,
(R为△ABC的外接圆半径).
∵2sin A+sin C=2sin B,∴2|BC|+|AB|=2|AC|,
由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点).
四.题型与方法
题型三 与双曲线有关的轨迹问题
求解双曲线的轨迹问题时要特别注意:(1)双曲线的焦点所在的坐标轴;(2)检验所求的轨迹对应的是双曲线的一支还是两支.
常见的方法:基本轨迹法
寻找几何关系,结合双曲线的定义,待定系数法得出对应的方程.
四.题型与方法
题型三 与双曲线有关的轨迹问题
[跟踪训练]3 如图所示,已知定圆F1:x2+y2+10x+24=0,定圆F2:x2+y2-10x+9=0,动圆M与定圆F1,F2都外切,求动圆圆心M的轨迹方程.
解:圆F1:(x+5)2+y2=1,圆心F1(-5,0),半径r1=1.圆F2:(x-5)2+y2=42,圆心F2(5,0),半径r2=4.设动圆M的半径为R,则有|MF1|=R+1,|MF2|=R+4,∴|MF2|-|MF1|=3<10=|F1F2|.∴点M的轨迹是以F1,F2为焦点的双曲线的左支,
双曲线两种标准方程的特点
① 方程用“-”号连接;
② 分母是a2, b2, 且a>0, b>0,但a, b大小不定;
③ c2=a2+b2 ;
④ 如果x2的系数是正的,则焦点在x轴上;
如果y2的系数是正的,则焦点在y轴上.
五.小结与练习
课堂小结
椭圆 双曲线
定 义
方 程 焦点在x轴上
焦点在y轴上
焦 点
a, b, c 的关系
F1(-c, 0), F2(c, 0)
a>0, b>0, c2=a2+b2 a, b, c中c最大
a>b>0, a2=b2+c2 a, b, c中a最大
双曲线与椭圆之间的区别与联系
||MF1|-|MF2||=2a (a
F1(0, -c), F2(0, c)
F1(-c, 0), F2(c, 0)
F1(0, -c), F2(0, c)
五.小结与练习
达标训练
五.小结与练习
1.动点P到点M(1,0)的距离与点N(3,0)的距离之差为2,则点P的轨迹是( )A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
2.已知F1(-8,3),F2(2,3),动点P满足|PF1|-|PF2|=10,则P点的轨迹是( )A.双曲线 B.双曲线的一支 C.直线 D.一条射线
D
D
D
五.小结与练习
C
C
A
8.已知双曲线方程为2x2-y2=k,焦距为6,则k的值为________.
9.已知F1,F2分别为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,则|PF1|·|PF2|等于________.
6或-6
4
五.小结与练习
