3.2.2双曲线的简单几何性质(第1课时)(教学课件)(共21张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质(第1课时)(教学课件)(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 14:36:35 | ||
图片预览






文档简介
(共21张PPT)
1.掌握双曲线的简单几何性质.
第 3 章圆锥曲线的方程
3.2.2 双曲线的简单几何性质(第1课时)
学习目标
2.理解双曲线的渐近线及离心率的意义.
3.掌握 双曲线“定义、图像、方程、性质”之间相互转化的方法.
双曲线的定义及标准方程
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
一.回顾与探究
类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质
如何研究这些性质
x
F1
F2
y
O
M(x,y)
F1
F2
O
x
y
A1
A2
B1
B2
椭圆的简单几何性质:①范围; ②对称性; ③顶点; ④离心率
本节,我们将类比椭圆研究双曲线性质
一.回顾与探究
类比研究椭圆范围的方法,观察双曲线,我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R (图3.2-7).
一、范围
二.双曲线的几何性质
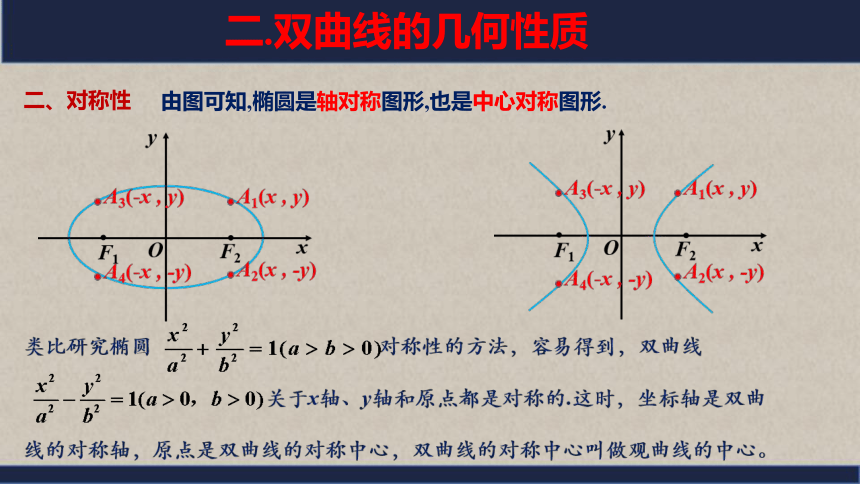
由图可知,椭圆是轴对称图形,也是中心对称图形.
二、对称性
二.双曲线的几何性质
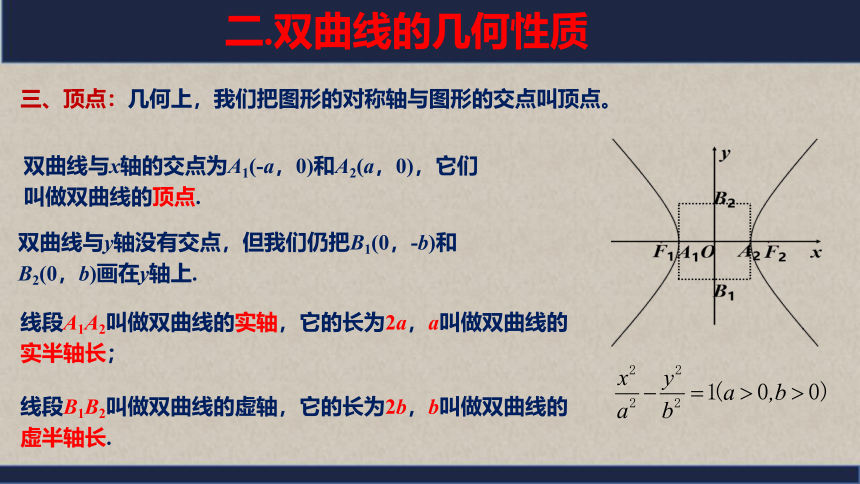
三、顶点:几何上,我们把图形的对称轴与图形的交点叫顶点。
双曲线与x轴的交点为A1(-a,0)和A2(a,0),它们叫做双曲线的顶点.
双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
二.双曲线的几何性质
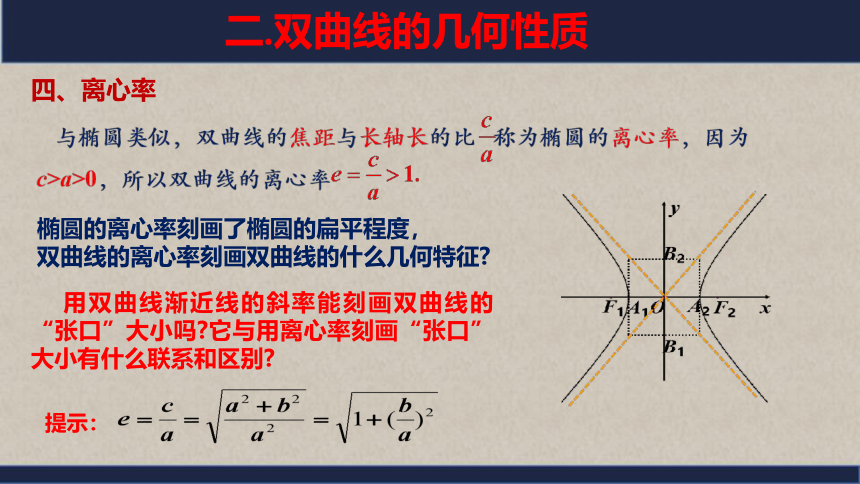
椭圆的离心率刻画了椭圆的扁平程度,
双曲线的离心率刻画双曲线的什么几何特征
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗 它与用离心率刻画“张口”大小有什么联系和区别
四、离心率
二.双曲线的几何性质
提示:
双曲线的两支向外延伸时,与矩形的两条对角线逐渐接近,我们把这两条直线叫做双曲线的渐近线.
五、渐近线
如图,直线x= a和直线y= b 围成了一个矩形,矩形的两条对角线的方程是什么?
这时,四条直线x =±a,y =±b围成正方形,渐近线方程为 y=±x ,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
二.双曲线的几何性质
双曲线标准方程:
双曲线性质:
1、范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点:
B1(0,-a), B2(0,-a)
4、对称轴:
5、渐近线方程:
6、离心率:
实轴 B1B2 ; 虚轴 A1A2
探究:焦点在y轴上的双曲线的几何性质都有什么?
二.双曲线的几何性质
(e>1 )
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
二.双曲线的几何性质
归纳总结:
1.知识要点:
以“定义 图像 方程 性质”为基本线索,以“定义、图像、方程、性质”为基本内容,以它们之间的相互转化为基本能力;
2.性质归纳:
(1)四类点:中心、焦点、顶点、虚轴端点;
(2)四类线:实轴、虚轴、渐近线、准线;
(3)五个基本量及其关系:a,b,c,e,p
3.由双曲线的方程研究其几何性质的注意点:
三.题型与方法
题型一 问题辨析
√
×
×
×
√
注意:
(1)共轭双曲线;等轴双曲线;共渐近线双曲线等概念及其性质;
(2)离心率及取值范围;
(3)顶点与虚轴端点;实轴长与a;虚轴长与b;双曲线与其渐近线的相互关系等。
三.题型与方法
题型二 根据双曲线方程研究几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
三.题型与方法
题型二 根据双曲线方程研究几何性质
由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准形式;(2)由标准方程确定焦点位置,确定a,b的值;(3)由c2=a2+b2求出c值,从而写出双曲线的几何性质.
提醒:求性质时一定要注意焦点的位置.
[跟踪训练]1求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
三.题型与方法
题型三 由几何性质求双曲线的标准方程
三.题型与方法
题型三 由几何性质求双曲线的标准方程
1.由几何性质求双曲线标准方程的解题思路:由双曲线的几何性质求双曲线的标准方程,一般用待定系数法.
当双曲线的焦点不明确时,方程可能有两种形式,此时应注意分类讨论;
为了避免讨论,也可设双曲线的方程为mx2-ny2=1(mn>0).
方法总结:
三.题型与方法
题型三 由几何性质求双曲线的标准方程
2.常见双曲线方程的设法:
三.题型与方法
题型三 由几何性质求双曲线的标准方程
三.题型与方法
题型四 求双曲线的离心率
三.题型与方法
题型四 求双曲线的离心率
求双曲线离心率的方法
四.达标训练
B
A
C
5
四.达标训练
1.掌握双曲线的简单几何性质.
第 3 章圆锥曲线的方程
3.2.2 双曲线的简单几何性质(第1课时)
学习目标
2.理解双曲线的渐近线及离心率的意义.
3.掌握 双曲线“定义、图像、方程、性质”之间相互转化的方法.
双曲线的定义及标准方程
标准方程
图 形
焦点坐标
双曲线定义
a、b、c 的关系
平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F1F2|)的点的轨迹.
一.回顾与探究
类比对椭圆几何性质的研究,你认为应该研究双曲线的哪些几何性质
如何研究这些性质
x
F1
F2
y
O
M(x,y)
F1
F2
O
x
y
A1
A2
B1
B2
椭圆的简单几何性质:①范围; ②对称性; ③顶点; ④离心率
本节,我们将类比椭圆研究双曲线性质
一.回顾与探究
类比研究椭圆范围的方法,观察双曲线,我们发现双曲线上点的横坐标的范围是x≤-a,或x≥a,纵坐标的范围是y∈R (图3.2-7).
一、范围
二.双曲线的几何性质
由图可知,椭圆是轴对称图形,也是中心对称图形.
二、对称性
二.双曲线的几何性质
三、顶点:几何上,我们把图形的对称轴与图形的交点叫顶点。
双曲线与x轴的交点为A1(-a,0)和A2(a,0),它们叫做双曲线的顶点.
双曲线与y轴没有交点,但我们仍把B1(0,-b)和B2(0,b)画在y轴上.
线段A1A2叫做双曲线的实轴,它的长为2a,a叫做双曲线的实半轴长;
线段B1B2叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长.
二.双曲线的几何性质
椭圆的离心率刻画了椭圆的扁平程度,
双曲线的离心率刻画双曲线的什么几何特征
用双曲线渐近线的斜率能刻画双曲线的“张口”大小吗 它与用离心率刻画“张口”大小有什么联系和区别
四、离心率
二.双曲线的几何性质
提示:
双曲线的两支向外延伸时,与矩形的两条对角线逐渐接近,我们把这两条直线叫做双曲线的渐近线.
五、渐近线
如图,直线x= a和直线y= b 围成了一个矩形,矩形的两条对角线的方程是什么?
这时,四条直线x =±a,y =±b围成正方形,渐近线方程为 y=±x ,它们互相垂直,并且平分双曲线实轴和虚轴所成的角.实轴和虚轴等长的双曲线叫做等轴双曲线.
二.双曲线的几何性质
双曲线标准方程:
双曲线性质:
1、范围:
y≥a或y≤-a
2、对称性:
关于x轴,y轴,原点对称。
3、顶点:
B1(0,-a), B2(0,-a)
4、对称轴:
5、渐近线方程:
6、离心率:
实轴 B1B2 ; 虚轴 A1A2
探究:焦点在y轴上的双曲线的几何性质都有什么?
二.双曲线的几何性质
(e>1 )
(1)把双曲线方程化为标准形式是解决此类题的关键.
(2)由标准方程确定焦点位置,确定a,b的值.
(3)由c2=a2+b2求出c的值,从而写出双曲线的几何性质.
二.双曲线的几何性质
归纳总结:
1.知识要点:
以“定义 图像 方程 性质”为基本线索,以“定义、图像、方程、性质”为基本内容,以它们之间的相互转化为基本能力;
2.性质归纳:
(1)四类点:中心、焦点、顶点、虚轴端点;
(2)四类线:实轴、虚轴、渐近线、准线;
(3)五个基本量及其关系:a,b,c,e,p
3.由双曲线的方程研究其几何性质的注意点:
三.题型与方法
题型一 问题辨析
√
×
×
×
√
注意:
(1)共轭双曲线;等轴双曲线;共渐近线双曲线等概念及其性质;
(2)离心率及取值范围;
(3)顶点与虚轴端点;实轴长与a;虚轴长与b;双曲线与其渐近线的相互关系等。
三.题型与方法
题型二 根据双曲线方程研究几何性质
例1 求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程.
三.题型与方法
题型二 根据双曲线方程研究几何性质
由双曲线的方程研究几何性质的解题步骤
(1)把双曲线方程化为标准形式;(2)由标准方程确定焦点位置,确定a,b的值;(3)由c2=a2+b2求出c值,从而写出双曲线的几何性质.
提醒:求性质时一定要注意焦点的位置.
[跟踪训练]1求双曲线9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.
三.题型与方法
题型三 由几何性质求双曲线的标准方程
三.题型与方法
题型三 由几何性质求双曲线的标准方程
1.由几何性质求双曲线标准方程的解题思路:由双曲线的几何性质求双曲线的标准方程,一般用待定系数法.
当双曲线的焦点不明确时,方程可能有两种形式,此时应注意分类讨论;
为了避免讨论,也可设双曲线的方程为mx2-ny2=1(mn>0).
方法总结:
三.题型与方法
题型三 由几何性质求双曲线的标准方程
2.常见双曲线方程的设法:
三.题型与方法
题型三 由几何性质求双曲线的标准方程
三.题型与方法
题型四 求双曲线的离心率
三.题型与方法
题型四 求双曲线的离心率
求双曲线离心率的方法
四.达标训练
B
A
C
5
四.达标训练
