2.1.1倾斜角与斜率 (教学课件)(15张PPT)
文档属性
| 名称 | 2.1.1倾斜角与斜率 (教学课件)(15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 00:00:00 | ||
图片预览





文档简介
2.1.1 倾斜角与斜率
高二上学期数学人教A版(2019)选择性必修第一册
学习目标
1、探索确定直线位置的几何要素,感受倾斜角这个反映倾斜程度的几何量的形成过程。
2、从生活中的坡度,自然迁移到数学中直线的斜率,感受数学概念来
源于生活实际,数学概念的形成是自然的
3、充分利用倾斜角和斜率是从数与形两方面,刻画直线相对于x轴倾斜程度的两个量这一事实
4、经历用代数方法刻画直线斜率的过程,初步掌握过已知两点的直线的斜率计算公式,
问题与思考
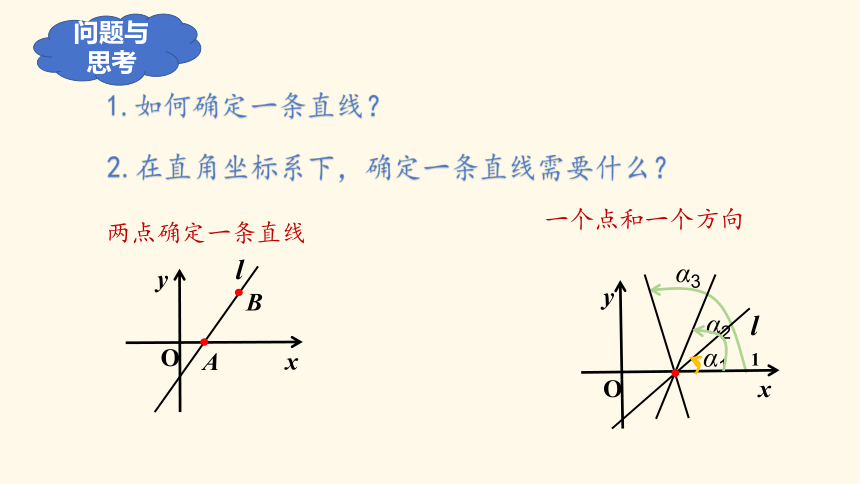
1.如何确定一条直线?
2.在直角坐标系下,确定一条直线需要什么?
l
x
y
O
A
B
l1
x
y
O
α1
α2
α3
两点确定一条直线
一个点和一个方向
画一画
在直角坐标系中,直线对x轴的相对位置有几种情形?画图表示。
3. 如何表示直线的方向?
在直角坐标系下,设????,????为直线上两点,则????????就是这条直线的方向向量。所以,两点确定一条直线也可以归结为一点和一个方向向量确定一条直线。
?
问题与思考
x
y
O
l
确定直线位置的要素除了点之外, 还有直线的方向, 也就是直线的倾斜程度.
O
x
y
P
α
α
(1)当直线l 与x轴相交时,我们取 x 轴为基准, x 轴正向与直线l 向上方向之间所形成的角α叫做直线l的倾斜角。
l
l
注意:
(1)直线向上方向;
(2)x轴的正方向。
(2)规定当直线l与x轴平行或重合时,规定它的倾斜角为0°
l
2、直线倾斜角α的取值范围:
0°≤α<180°
倾斜角相同能确定一条直线吗?
x
o
y
一点+倾斜角 确定一条直线
(两者缺一不可)
定 义
探究
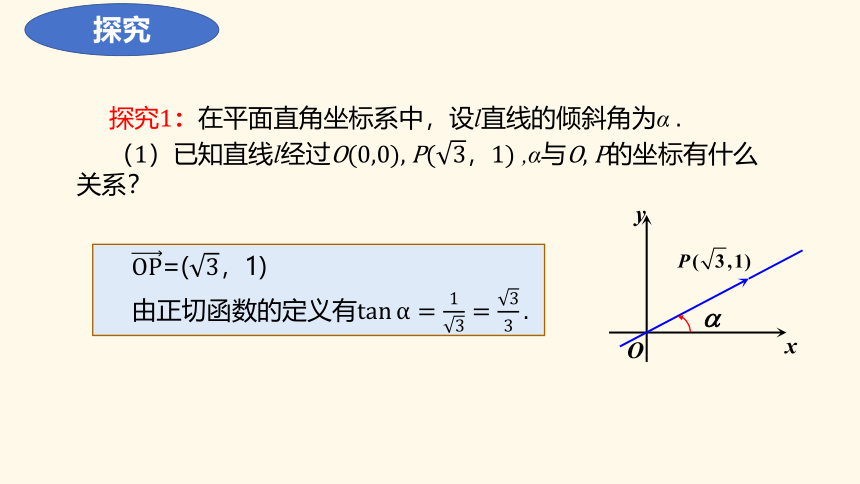
探究1:在平面直角坐标系中,设l直线的倾斜角为α .
(1)已知直线l经过O(0,0), P(3,1) ,α与O, P的坐标有什么关系?
?
O
x
y
OP=(3,1)
由正切函数的定义有tanα=13=33.
?
探究2:在平面直角坐标系中,设l直线的倾斜角为α .
(2)类似地,若直线l经过????1(?1,1), ????2(2,0) ,α与????1, ????2的坐标又有什么关系?
?
探究
O
x
y
P
P2P1=(?1?2,1 ??0)=(?1?2,1).
平移向量P2P1到OP
则点P的坐标为(?1?2,1),
由正切函数的定义有tanα=1?1?2=1?2
?
探究3:一般地,若直线l经过????1(????1,????1), ????2(????2, ????2)(????1≠ ????2) ,那么α与????1, ????2的坐标有怎样的关系?
?
探究
当向量P1P2,的方向向上时,P1P2=(????2?????1,????2?????1).平移向量P1P2到OP,则点P的坐标为(????2?????1,????2?????1),且直线OP的倾斜角也是α,由正切函数的定义,有tanα=????2?????1????2?????1.
?
O
x
y
P1
P2
O
x
y
P2
P1
意 义
前进量
升
高
量
直线????的倾斜角????与直线????上的两点????1(????1,????1),????2(????2,????2)(????1≠????2)的坐标有如下关系:?????????????????=????2?????1????2?????1.①
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即k=tan?α.②
?
图示
?
?
?
?
倾斜角(范围)
α=0°
0°<α<90°
α=90°
90°<α<180°
斜率(范围)
k=0
k>0
不存在
k<0
斜率与倾斜角对应关系
意 义
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角????
0°
30°
45°
60°
120°
135°
150°
斜率????
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
0°
30°
45°
60°
120°
135°
150°
填一填
思考:直线的倾斜角越大,斜率越大?
????∈[0°,90°)时,斜率越大,倾斜角越大;
????∈(90°,180°)时,斜率越大,倾斜角越大.
?
斜率范围:????∈(-∞,+∞)
?
辨析1:判断正误.
(1)倾斜角为135°的直线的斜率为1.( )
(2)直线斜率的取值范围是(?∞,+∞).( )
?
×
辨析2:如图所示, 直线l的倾斜角为( ).
????.60° ????.150° ????.0° ????.不存在
?
????
?
练习
√
例1:如图,已知A(3,2),B(?4,1),C(0,?1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
?
解:直线AB的斜率kAB=1?2?4?3=?1?7=17;
直线BC的斜率kBC=?1?10?(?4)=?24=?12;
直线CA的斜率kCA=2?(?1)3?0=33=1.
由kAB>0及kCA>0可知,直线AB与CA的倾斜角均为锐角;
由kBC<0可知,直线BC的倾斜角为钝角.
?
例题讲解
小节
图示
?
?
?
?
倾斜角(范围)
α=0°
0°<α<90°
α=90°
90°<α<180°
斜率(范围)
k=0
k>0
不存在
k<0
斜率与倾斜角对应关系
k=tan?α=????2?????1????2?????1
?
????∈[0°,90°)时,斜率越大,倾斜角越大;
????∈(90°,180°)时,斜率越大,倾斜角越大.
?
斜率范围:????∈(-∞,+∞)
高二上学期数学人教A版(2019)选择性必修第一册
学习目标
1、探索确定直线位置的几何要素,感受倾斜角这个反映倾斜程度的几何量的形成过程。
2、从生活中的坡度,自然迁移到数学中直线的斜率,感受数学概念来
源于生活实际,数学概念的形成是自然的
3、充分利用倾斜角和斜率是从数与形两方面,刻画直线相对于x轴倾斜程度的两个量这一事实
4、经历用代数方法刻画直线斜率的过程,初步掌握过已知两点的直线的斜率计算公式,
问题与思考
1.如何确定一条直线?
2.在直角坐标系下,确定一条直线需要什么?
l
x
y
O
A
B
l1
x
y
O
α1
α2
α3
两点确定一条直线
一个点和一个方向
画一画
在直角坐标系中,直线对x轴的相对位置有几种情形?画图表示。
3. 如何表示直线的方向?
在直角坐标系下,设????,????为直线上两点,则????????就是这条直线的方向向量。所以,两点确定一条直线也可以归结为一点和一个方向向量确定一条直线。
?
问题与思考
x
y
O
l
确定直线位置的要素除了点之外, 还有直线的方向, 也就是直线的倾斜程度.
O
x
y
P
α
α
(1)当直线l 与x轴相交时,我们取 x 轴为基准, x 轴正向与直线l 向上方向之间所形成的角α叫做直线l的倾斜角。
l
l
注意:
(1)直线向上方向;
(2)x轴的正方向。
(2)规定当直线l与x轴平行或重合时,规定它的倾斜角为0°
l
2、直线倾斜角α的取值范围:
0°≤α<180°
倾斜角相同能确定一条直线吗?
x
o
y
一点+倾斜角 确定一条直线
(两者缺一不可)
定 义
探究
探究1:在平面直角坐标系中,设l直线的倾斜角为α .
(1)已知直线l经过O(0,0), P(3,1) ,α与O, P的坐标有什么关系?
?
O
x
y
OP=(3,1)
由正切函数的定义有tanα=13=33.
?
探究2:在平面直角坐标系中,设l直线的倾斜角为α .
(2)类似地,若直线l经过????1(?1,1), ????2(2,0) ,α与????1, ????2的坐标又有什么关系?
?
探究
O
x
y
P
P2P1=(?1?2,1 ??0)=(?1?2,1).
平移向量P2P1到OP
则点P的坐标为(?1?2,1),
由正切函数的定义有tanα=1?1?2=1?2
?
探究3:一般地,若直线l经过????1(????1,????1), ????2(????2, ????2)(????1≠ ????2) ,那么α与????1, ????2的坐标有怎样的关系?
?
探究
当向量P1P2,的方向向上时,P1P2=(????2?????1,????2?????1).平移向量P1P2到OP,则点P的坐标为(????2?????1,????2?????1),且直线OP的倾斜角也是α,由正切函数的定义,有tanα=????2?????1????2?????1.
?
O
x
y
P1
P2
O
x
y
P2
P1
意 义
前进量
升
高
量
直线????的倾斜角????与直线????上的两点????1(????1,????1),????2(????2,????2)(????1≠????2)的坐标有如下关系:?????????????????=????2?????1????2?????1.①
我们把一条直线的倾斜角α的正切值叫做这条直线的斜率.斜率常用小写字母k表示,即k=tan?α.②
?
图示
?
?
?
?
倾斜角(范围)
α=0°
0°<α<90°
α=90°
90°<α<180°
斜率(范围)
k=0
k>0
不存在
k<0
斜率与倾斜角对应关系
意 义
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角????
0°
30°
45°
60°
120°
135°
150°
斜率????
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}
0°
30°
45°
60°
120°
135°
150°
填一填
思考:直线的倾斜角越大,斜率越大?
????∈[0°,90°)时,斜率越大,倾斜角越大;
????∈(90°,180°)时,斜率越大,倾斜角越大.
?
斜率范围:????∈(-∞,+∞)
?
辨析1:判断正误.
(1)倾斜角为135°的直线的斜率为1.( )
(2)直线斜率的取值范围是(?∞,+∞).( )
?
×
辨析2:如图所示, 直线l的倾斜角为( ).
????.60° ????.150° ????.0° ????.不存在
?
????
?
练习
√
例1:如图,已知A(3,2),B(?4,1),C(0,?1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角.
?
解:直线AB的斜率kAB=1?2?4?3=?1?7=17;
直线BC的斜率kBC=?1?10?(?4)=?24=?12;
直线CA的斜率kCA=2?(?1)3?0=33=1.
由kAB>0及kCA>0可知,直线AB与CA的倾斜角均为锐角;
由kBC<0可知,直线BC的倾斜角为钝角.
?
例题讲解
小节
图示
?
?
?
?
倾斜角(范围)
α=0°
0°<α<90°
α=90°
90°<α<180°
斜率(范围)
k=0
k>0
不存在
k<0
斜率与倾斜角对应关系
k=tan?α=????2?????1????2?????1
?
????∈[0°,90°)时,斜率越大,倾斜角越大;
????∈(90°,180°)时,斜率越大,倾斜角越大.
?
斜率范围:????∈(-∞,+∞)
