2.1.1直线的倾斜角与斜率 (教学课件)(共39张PPT)
文档属性
| 名称 | 2.1.1直线的倾斜角与斜率 (教学课件)(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 15:32:58 | ||
图片预览





文档简介
解析几何
第二章 直线和圆的方程
问题1: 我们学过哪些平面图形,用的什么研究方法?
问题1: 我们学过哪些平面图形,用的什么研究方法?
综合法
引 入
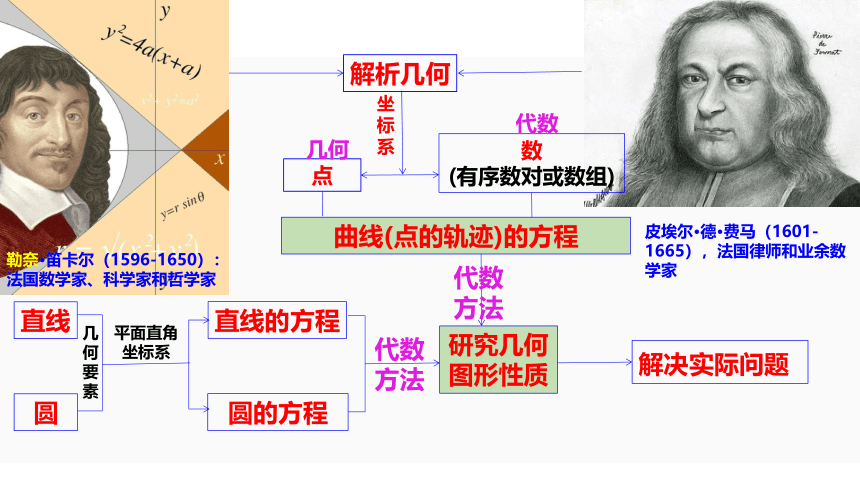
解析几何
勒奈·笛卡尔(1596-1650):法国数学家、科学家和哲学家
皮埃尔·德·费马(1601-1665),法国律师和业余数学家
坐标系
点
数
(有序数对或数组)
几何
代数
曲线(点的轨迹)的方程
研究几何图形性质
代数方法
直线
直线的方程
几何要素
圆的方程
解决实际问题
圆
平面直角坐标系
代数方法
2.1.1 直线的倾斜角与斜率
第二章 直线和圆的方程
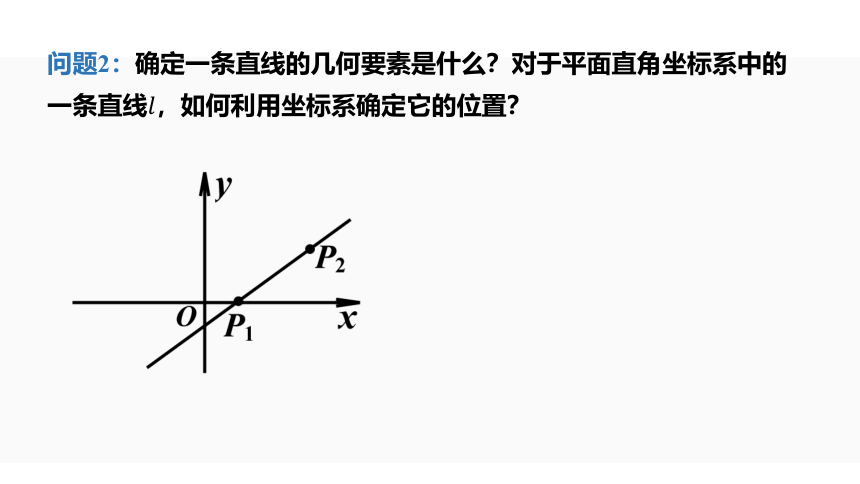
问题2:确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线????,如何利用坐标系确定它的位置?
?
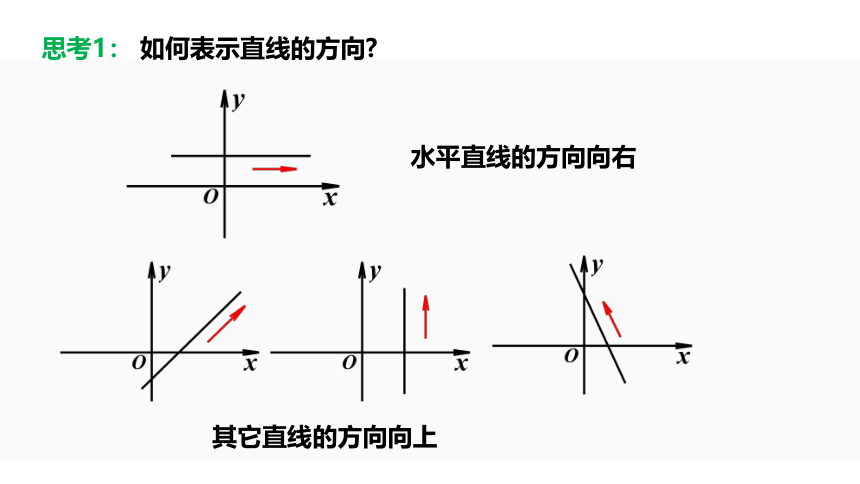
水平直线的方向向右
思考1: 如何表示直线的方向?
其它直线的方向向上
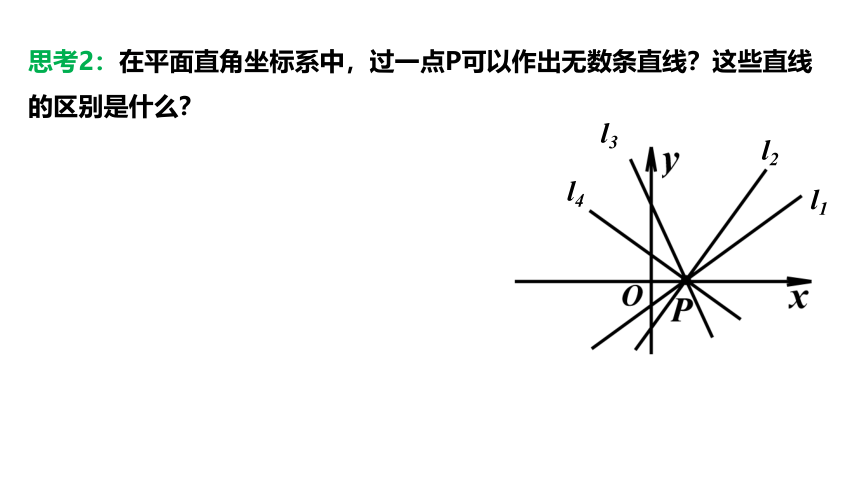
思考2:在平面直角坐标系中,过一点P可以作出无数条直线?这些直线的区别是什么?
l1
l2
l3
l4
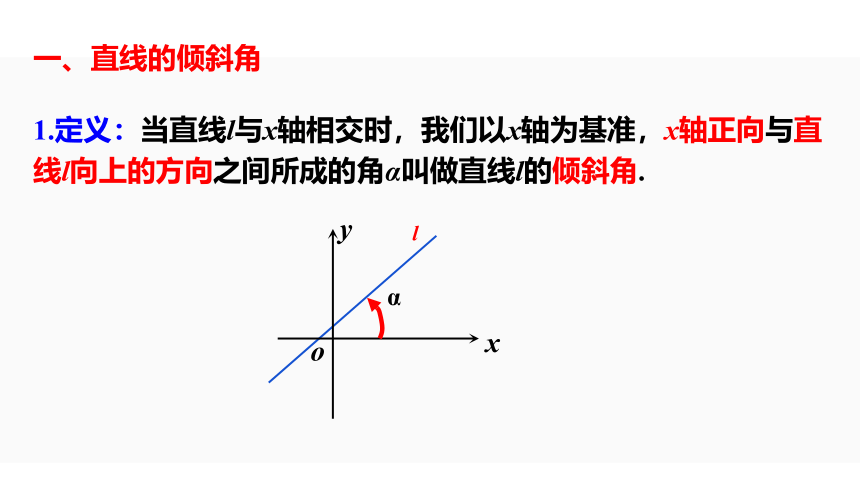
一、直线的倾斜角
1.定义:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
x
y
o
α
l
零度角
锐角
直角
钝角
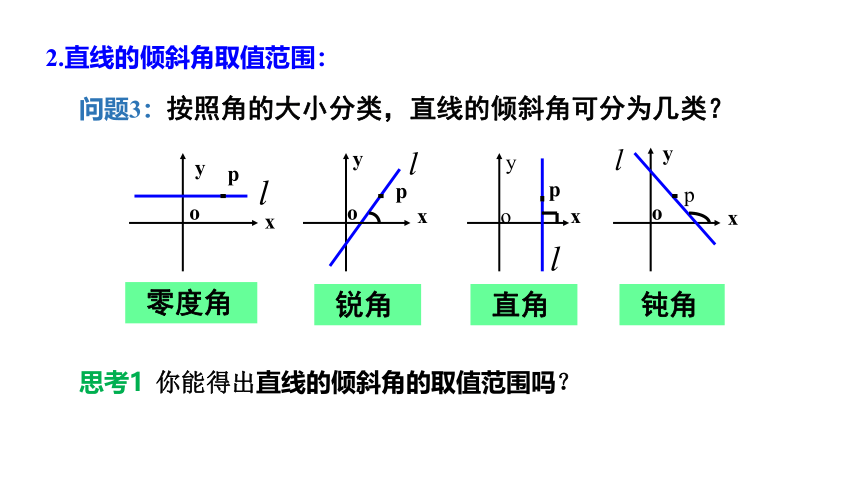
问题3:按照角的大小分类,直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
2.直线的倾斜角取值范围:
思考1 你能得出直线的倾斜角的取值范围吗?
零度角
锐角
直角
钝角
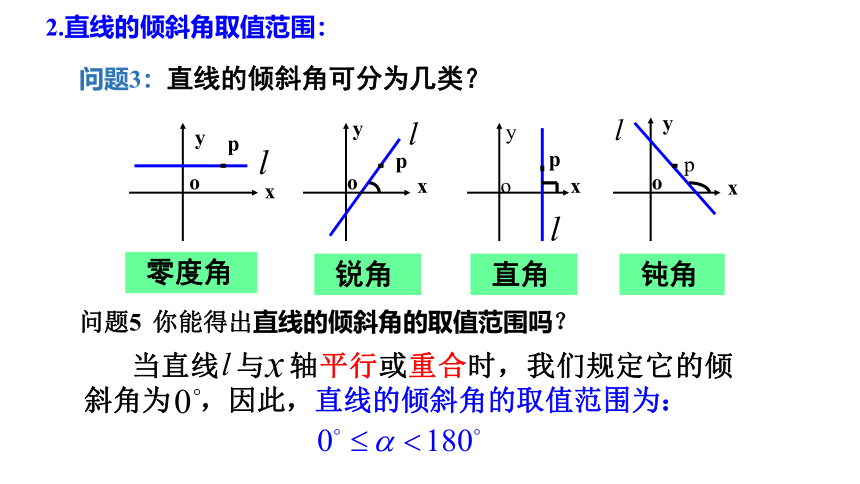
问题3:直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
2.直线的倾斜角取值范围:
问题5 你能得出直线的倾斜角的取值范围吗?
问题4 任何一条直线都有唯一确定的倾斜角与它对应吗?
O
y
x
l1
α1
l2
l3
α2
α3
每一个倾斜角都对应于唯一的一条直线吗?
不同的直线其倾斜角一 定不相同吗?
直线l
唯一倾斜角α
方向相同的直线(平行或重合)
倾斜角α
思考1 确定一条直线的几何要素还可以是什么?
一个点P和一个倾斜角? .
3. 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°得到直线l′,则直线l′的倾斜角为( )
A. α+45° B. α-135°
C. 135°-α D.当0°≤α<135°时为α+45°,当135°≤α<180°时为α-135°
1. 下图中,表示直线的倾斜角的是( )
A
B
C
D
2. 若直线l的向上方向与y轴的正方向成30°角, 则直线l的倾斜角为( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
类型一 直线的倾斜角
3. 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°得到直线l′,则直线l′的倾斜角为( )
A. α+45° B. α-135°
C. 135°-α D.当0°≤α<135°时为α+45°,当135°≤α<180°时为α-135°
1. 下图中,表示直线的倾斜角的是( )
A
B
C
D
A
2. 若直线l的向上方向与y轴的正方向成30°角, 则直线l的倾斜角为( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
D
D
类型一 直线的倾斜角
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
O
y
x
α
O
y
x
α
α
?
?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
(3) 一般地,如果直线l经过P1(x1, y1), P2(x2, y2),(其中 x1≠x2)α与P1, P2的坐标有怎样的关系吗?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(3) 一般地,如果直线l经过P1(x1, y1), P2(x2, y2),(其中 x1≠x2)α与P1, P2的坐标有怎样的关系吗?
O
y
x
α
?
?
O
x
y
P1
P2
α
O
x
y
P
P2
P1
思考1 上述式子与P1, P2的顺序有关吗?
思考2 当直线P1P2与x轴平行或重合时,上述式子还成立吗?
思考3 当直线P1P2与y轴平行或重合时,上述式子还成立吗?
1.定义:我们把一条直线的倾斜角? 的正切值叫做这条直线的斜率,用小写字母 k 表示,即k=tanα .
α∈[0° ,90° ) ∪(90° ,180° )
2.公式:直线过P1(x1, y1), P2(x2, y2), x1≠x2,
(x1≠x2)
二、直线的斜率
延时符
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角α
0°
30°
45°
90°
120°
150°
斜率k
3.常见角对应的斜率:
延时符
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角α
0°
30°
45°
60°
90°
120°
135°
150°
斜率k
3.常见角对应的斜率:
不存在
x
y
o
P(2,2)
问题5 如图,当直线l绕点P(2,2)逆时针旋转时,直线l的倾斜角如何变化,
其斜率如何变化?
l
1.思考辨析(在括号内打“√”或“×”)
(1)直线的倾斜角越大,其斜率就越大.( )
(2)直线的斜率越大,其倾斜角就越大.( )
(3)直线的斜率为tan α,则其倾斜角为α.( )
(4)直线的倾斜角为α,则其斜率为tan α.( )
(5)斜率相等的两直线的倾斜角一定相等.( )
(6)倾斜角相等的两直线的斜率一定相等.( )
(7)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线的斜率为
????=??????????????????????????????????.( )
?
诊断自测
1.思考辨析(在括号内打“√”或“×”)
(1)直线的倾斜角越大,其斜率就越大.( )
(2)直线的斜率越大,其倾斜角就越大.( )
(3)直线的斜率为tan α,则其倾斜角为α.( )
(4)直线的倾斜角为α,则其斜率为tan α.( )
(5)斜率相等的两直线的倾斜角一定相等.( )
(6)倾斜角相等的两直线的斜率一定相等.( )
(7)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线的斜率为????=??????????????????????????????????.( )
?
×
诊断自测
×
×
×
√
×
×
例1 如图, 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断这些直线的倾斜角是锐角还是钝角.
O
y
x
A(3,2)
B(-4,1)
C(0,-1)
1
-1
-2
类型二 直线的斜率
变式 若点D在BC(包括端点)上移动时,求直线AD的斜率的变化范围
例1 如图示, 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断这些直线的倾斜角是锐角还是钝角.
O
y
x
A(3,2)
B(-4,1)
C(0,-1)
1
-1
-2
例2 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
类型二 直线的斜率
(2)求直线l的倾斜角α的取值范围.
例2 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
要使直线l与线段AB有公共点,
则直线l的斜率k的取值范围是(-∞,-1]∪[1,+∞).
(2)求直线l的倾斜角α的取值范围.
由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又直线PB的倾斜角是45°,直线PA的倾斜角是135°,
所以α的取值范围是45°≤α≤135°.
问题6 直线的方向向量与斜率?????有什么关系?
?
思考2 若直线????的斜率为?????,如何用斜率表示它的一个方向向量的坐标?
?
思考1 若直线????的一个方向向量为(????,????),如何求其斜率??????
?
问题6 直线的方向向量与斜率?????有什么关系?
?
思考2 若直线????的斜率为?????,如何用斜率表示它的一个方向向量的坐标?
(1, k).
?
思考1 若直线????的一个方向向量为(????,????),如何求其斜率??????
k=????????.
?
例3 经过A(0, 2), B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
类型二 直线的斜率
变式 已知直线l的一个方向向量为 求直线l的倾斜角和斜率.
例3 经过A(0, 2), B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
类型二 直线的斜率
变式 已知直线l的一个方向向量为 求直线l的倾斜角和斜率.
是直线l的一个方向向量,
即
又
∴直线l的倾斜角为 ,斜率为
解:
【提升训练】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
类型二 直线的斜率
【提升训练】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
解:
A(0,2), B(0, -1),
当m=0时,
直线AB倾斜角α=90°. 符合题意.
直线AB⊥x轴,
直线AB的斜率为
当m≠0时,
或
或
解得
故m的取值范围为
即
或
类型二 直线的斜率
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .
k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.
追问:那么“坡度”是如何来刻画道路的倾斜程度的呢?
三、直线斜率的实际应用
THANKS
第二章 直线和圆的方程
问题1: 我们学过哪些平面图形,用的什么研究方法?
问题1: 我们学过哪些平面图形,用的什么研究方法?
综合法
引 入
解析几何
勒奈·笛卡尔(1596-1650):法国数学家、科学家和哲学家
皮埃尔·德·费马(1601-1665),法国律师和业余数学家
坐标系
点
数
(有序数对或数组)
几何
代数
曲线(点的轨迹)的方程
研究几何图形性质
代数方法
直线
直线的方程
几何要素
圆的方程
解决实际问题
圆
平面直角坐标系
代数方法
2.1.1 直线的倾斜角与斜率
第二章 直线和圆的方程
问题2:确定一条直线的几何要素是什么?对于平面直角坐标系中的一条直线????,如何利用坐标系确定它的位置?
?
水平直线的方向向右
思考1: 如何表示直线的方向?
其它直线的方向向上
思考2:在平面直角坐标系中,过一点P可以作出无数条直线?这些直线的区别是什么?
l1
l2
l3
l4
一、直线的倾斜角
1.定义:当直线l与x轴相交时,我们以x轴为基准,x轴正向与直线l向上的方向之间所成的角α叫做直线l的倾斜角.
x
y
o
α
l
零度角
锐角
直角
钝角
问题3:按照角的大小分类,直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
2.直线的倾斜角取值范围:
思考1 你能得出直线的倾斜角的取值范围吗?
零度角
锐角
直角
钝角
问题3:直线的倾斜角可分为几类?
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
当直线 与 轴平行或重合时,我们规定它的倾斜角为 ,因此,直线的倾斜角的取值范围为:
2.直线的倾斜角取值范围:
问题5 你能得出直线的倾斜角的取值范围吗?
问题4 任何一条直线都有唯一确定的倾斜角与它对应吗?
O
y
x
l1
α1
l2
l3
α2
α3
每一个倾斜角都对应于唯一的一条直线吗?
不同的直线其倾斜角一 定不相同吗?
直线l
唯一倾斜角α
方向相同的直线(平行或重合)
倾斜角α
思考1 确定一条直线的几何要素还可以是什么?
一个点P和一个倾斜角? .
3. 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°得到直线l′,则直线l′的倾斜角为( )
A. α+45° B. α-135°
C. 135°-α D.当0°≤α<135°时为α+45°,当135°≤α<180°时为α-135°
1. 下图中,表示直线的倾斜角的是( )
A
B
C
D
2. 若直线l的向上方向与y轴的正方向成30°角, 则直线l的倾斜角为( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
类型一 直线的倾斜角
3. 设直线l过原点,其倾斜角为α,将直线l绕坐标原点沿逆时针方向旋转45°得到直线l′,则直线l′的倾斜角为( )
A. α+45° B. α-135°
C. 135°-α D.当0°≤α<135°时为α+45°,当135°≤α<180°时为α-135°
1. 下图中,表示直线的倾斜角的是( )
A
B
C
D
A
2. 若直线l的向上方向与y轴的正方向成30°角, 则直线l的倾斜角为( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
D
D
类型一 直线的倾斜角
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
O
y
x
α
O
y
x
α
α
?
?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(1) 已知直线l经过O(0, 0), P( , 1), α与O, P 的坐标有什么关系?
(2) 类似地,如果直线l经过P1(-1, 1), P2( , 0), α与P1, P2的坐标又有什么关系?
(3) 一般地,如果直线l经过P1(x1, y1), P2(x2, y2),(其中 x1≠x2)α与P1, P2的坐标有怎样的关系吗?
探究 在两点确定一条直线,接下来探究直线倾斜角与直线上两点坐标有何关系:
平面直角坐标系中,设直线l的倾斜角为α,(请用向量法探究下面问题)
(3) 一般地,如果直线l经过P1(x1, y1), P2(x2, y2),(其中 x1≠x2)α与P1, P2的坐标有怎样的关系吗?
O
y
x
α
?
?
O
x
y
P1
P2
α
O
x
y
P
P2
P1
思考1 上述式子与P1, P2的顺序有关吗?
思考2 当直线P1P2与x轴平行或重合时,上述式子还成立吗?
思考3 当直线P1P2与y轴平行或重合时,上述式子还成立吗?
1.定义:我们把一条直线的倾斜角? 的正切值叫做这条直线的斜率,用小写字母 k 表示,即k=tanα .
α∈[0° ,90° ) ∪(90° ,180° )
2.公式:直线过P1(x1, y1), P2(x2, y2), x1≠x2,
(x1≠x2)
二、直线的斜率
延时符
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角α
0°
30°
45°
90°
120°
150°
斜率k
3.常见角对应的斜率:
延时符
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}倾斜角α
0°
30°
45°
60°
90°
120°
135°
150°
斜率k
3.常见角对应的斜率:
不存在
x
y
o
P(2,2)
问题5 如图,当直线l绕点P(2,2)逆时针旋转时,直线l的倾斜角如何变化,
其斜率如何变化?
l
1.思考辨析(在括号内打“√”或“×”)
(1)直线的倾斜角越大,其斜率就越大.( )
(2)直线的斜率越大,其倾斜角就越大.( )
(3)直线的斜率为tan α,则其倾斜角为α.( )
(4)直线的倾斜角为α,则其斜率为tan α.( )
(5)斜率相等的两直线的倾斜角一定相等.( )
(6)倾斜角相等的两直线的斜率一定相等.( )
(7)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线的斜率为
????=??????????????????????????????????.( )
?
诊断自测
1.思考辨析(在括号内打“√”或“×”)
(1)直线的倾斜角越大,其斜率就越大.( )
(2)直线的斜率越大,其倾斜角就越大.( )
(3)直线的斜率为tan α,则其倾斜角为α.( )
(4)直线的倾斜角为α,则其斜率为tan α.( )
(5)斜率相等的两直线的倾斜角一定相等.( )
(6)倾斜角相等的两直线的斜率一定相等.( )
(7)经过任意两个不同的点P1(x1,y1),P2(x2,y2)的直线的斜率为????=??????????????????????????????????.( )
?
×
诊断自测
×
×
×
√
×
×
例1 如图, 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断这些直线的倾斜角是锐角还是钝角.
O
y
x
A(3,2)
B(-4,1)
C(0,-1)
1
-1
-2
类型二 直线的斜率
变式 若点D在BC(包括端点)上移动时,求直线AD的斜率的变化范围
例1 如图示, 已知A(3, 2), B(-4, 1), C(0, -1), 求直线AB, BC, CA的斜率, 并判断这些直线的倾斜角是锐角还是钝角.
O
y
x
A(3,2)
B(-4,1)
C(0,-1)
1
-1
-2
例2 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
类型二 直线的斜率
(2)求直线l的倾斜角α的取值范围.
例2 已知两点A(-3,4),B(3,2),过点P(1,0)的直线l与线段AB有公共点.
(1)求直线l的斜率k的取值范围;
要使直线l与线段AB有公共点,
则直线l的斜率k的取值范围是(-∞,-1]∪[1,+∞).
(2)求直线l的倾斜角α的取值范围.
由题意可知直线l的倾斜角介于直线PB与PA的倾斜角之间,又直线PB的倾斜角是45°,直线PA的倾斜角是135°,
所以α的取值范围是45°≤α≤135°.
问题6 直线的方向向量与斜率?????有什么关系?
?
思考2 若直线????的斜率为?????,如何用斜率表示它的一个方向向量的坐标?
?
思考1 若直线????的一个方向向量为(????,????),如何求其斜率??????
?
问题6 直线的方向向量与斜率?????有什么关系?
?
思考2 若直线????的斜率为?????,如何用斜率表示它的一个方向向量的坐标?
(1, k).
?
思考1 若直线????的一个方向向量为(????,????),如何求其斜率??????
k=????????.
?
例3 经过A(0, 2), B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
类型二 直线的斜率
变式 已知直线l的一个方向向量为 求直线l的倾斜角和斜率.
例3 经过A(0, 2), B(-1, 0)两点的直线的方向向量为(1, k),求k的值.
类型二 直线的斜率
变式 已知直线l的一个方向向量为 求直线l的倾斜角和斜率.
是直线l的一个方向向量,
即
又
∴直线l的倾斜角为 ,斜率为
解:
【提升训练】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
类型二 直线的斜率
【提升训练】已知经过A(m,2), B(-m,2m-1)的直线的倾斜角为α, 且45°<α<135°, 试求实数m的取值范围.
解:
A(0,2), B(0, -1),
当m=0时,
直线AB倾斜角α=90°. 符合题意.
直线AB⊥x轴,
直线AB的斜率为
当m≠0时,
或
或
解得
故m的取值范围为
即
或
类型二 直线的斜率
交通工程上一般用“坡度”来描述一段道路对于水平方向的倾斜程度,如图,一辆汽车沿某条道路从A点前进到B点,在水平方向前进的距离为AD,竖直方向上升的高度为DB(如果是下降,则DB的值为负实数),则坡度 .
k>0表示上坡,k<0表示下坡,为了实际应用与安全,在道路铺设时常要规划坡度的大小.
追问:那么“坡度”是如何来刻画道路的倾斜程度的呢?
三、直线斜率的实际应用
THANKS
