人教A版(2019)选择性必修第一册 2.2.2直线的两点式方程 课件(共18张PPT)
文档属性
| 名称 | 人教A版(2019)选择性必修第一册 2.2.2直线的两点式方程 课件(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 623.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 17:12:05 | ||
图片预览





文档简介
(共18张PPT)
2.2.2直线的两点式方程
学习目标
1.掌握直线方程的两点式的形式,了解其适用范围.
2.了解直线方程截距式的形式,特征及其适用范围(重点).
3.会用中点坐标公式求线段的中点坐标(重点).
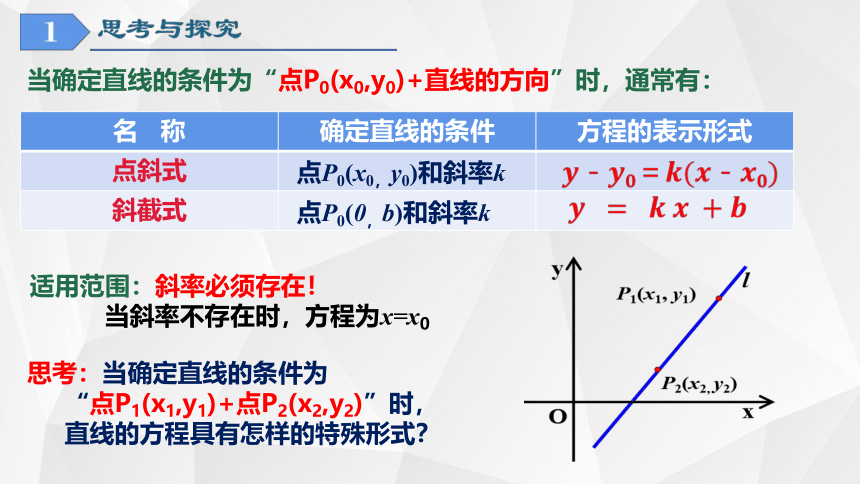
名 称 确定直线的条件 方程的表示形式
点斜式
斜截式
点P0(x0,y0)和斜率k
点P0(0,b)和斜率k
当确定直线的条件为“点P0(x0,y0)+直线的方向”时,通常有:
适用范围:斜率必须存在!
当斜率不存在时,方程为x=x0
思考:当确定直线的条件为
“点P1(x1,y1)+点P2(x2,y2)”时,
直线的方程具有怎样的特殊形式?
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2没有两点式方程。
x=x1
y=y1
两点式的适用范围:斜率存在且斜率不为0!
当x1=x2时,直线P1P2垂直于x轴,直线方程为x-x1=0,即x=x1;
当y1=y2时,直线P1P2垂直于y轴,直线方程为y-y1=0,即y=y1。
直线的两点式方程具有“对称、整齐”的特征,是直线方程的又一特殊形式;
思考:下列方程是否为过两点P1(x1,y1),P2(x2,y2)的直线方程?能否称为“两点式”?
中点坐标公式:
线段P1P2中P1(x1, y1), P2(x2, y2), 则中点P(x,y) :
重心坐标公式:
在 △ABC中A(x1, y1), B(x2, y2), C(x3, y3), 则重心G(x,y) :
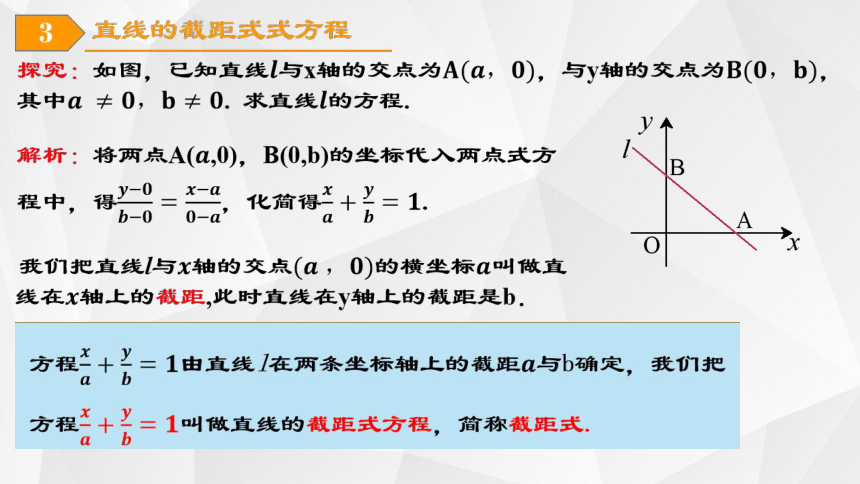
思考:直角坐标平面内的所有直线都可表示为截距式吗?考查下列特殊情形,你能得到什么结论?
(1)直线l垂直于x轴:
(3)直线l经过坐标原点:
(2)直线l垂直于y轴:
x=a
y=b
y=kx
截距式适用范围:直线l与两坐标轴不垂直且不过原点的直线。
回答:若直线l在两坐标轴上的截距相等,则直线l的方程:
x+y=a或y=kx
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)三角形三边所在直线的方程;
题型一 直线的两点式方程
解:直线AB:
直线BC:
直线AC:
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(2)BC边上中线AM所在直线的方程;
题型一 直线的两点式方程
M
解:
题型一 直线的两点式方程
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(3)BC边垂直平分线l所在直线的方程.
M
解:
注意:当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不平行于坐标轴.若满足,则考虑用两点式求方程.
[跟踪训练] 1 (1)过(1,1),(2,-1)两点的直线方程为( )A.2x-y-1=0 B.x-2y+3=0C.2x+y-3=0 D.x+2y-3=0(2) 经过M(3,2)与N(6,2)两点的直线方程为( )A.x=2 B.y=2 C.x=3 D.x=6
题型一 直线的两点式方程
(3)如图,已知A(1,2),B(-1,4),C(5,2).①求线段AB中点D的坐标;②求△ABC的边AB上的中线所在的直线方程.
(3)解 ①线段AB中点D的坐标为D(0,3).②△ABC的边AB上的中线所在的直线方程为
x+5y-15=0.
答案:C
答案:B
题型二 直线的截距式方程
例2 求过点A(3,4),且在两坐标轴上的截距截距相等的直线l的方程。
题型二 直线的截距式方程
注意: (1)如果问题中涉及直线与两坐标轴相交,则可考虑选用直线截距式的方程,用待定系数法确定其系数即可.(2)选用直线截距式的方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.如果题目中出现直线在两坐标轴上的“截距相等”、“截距互为相反数”、“在一坐标轴上的截距是另一坐标轴上截距的m倍(m>0)”等条件时,采用截距式求直线方程,要考虑“零截距”的情况.
[跟踪训练] 2 (1)求过点A(4,2),且在两坐标轴上的截距的绝对值相等的直线l的方程.
题型二 直线的截距式方程
[跟踪训练] 2 (2)已知直线l过点A(1,2),且与两坐标轴的正半轴围成的三角形的面积是4,求直线l的方程.
1.点斜式方程:
y-y0=k(x-x0) (已知定点(x0, y0)及斜率k存在)
2. 斜截式方程:
y=kx+b [已知k存在及截距 b(与y轴交点(0, b)]
3. 两点式方程:
[已知两定点(不适合与x轴或y轴垂直的直线)]
4. 截距式方程:
[已知截距a(与x轴交点(a,0))及截距b(与y轴交点(0, b))不适合过原点的直线]
【当堂达标】
答案:A
答案:A
答案:B
4.已知点A(3,2),B(-1,4),则经过点C(2,5)且经过线段AB的中点的直线方程为________.
5.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为_________ .
6.直线l经过点A(-3,4),且在x轴上的截距是在y轴上的截距的2倍,求该直线的方程.
【当堂达标】
2.2.2直线的两点式方程
学习目标
1.掌握直线方程的两点式的形式,了解其适用范围.
2.了解直线方程截距式的形式,特征及其适用范围(重点).
3.会用中点坐标公式求线段的中点坐标(重点).
名 称 确定直线的条件 方程的表示形式
点斜式
斜截式
点P0(x0,y0)和斜率k
点P0(0,b)和斜率k
当确定直线的条件为“点P0(x0,y0)+直线的方向”时,通常有:
适用范围:斜率必须存在!
当斜率不存在时,方程为x=x0
思考:当确定直线的条件为
“点P1(x1,y1)+点P2(x2,y2)”时,
直线的方程具有怎样的特殊形式?
在P1(x1,y1),P2(x2,y2)中,如果x1=x2或y1=y2,则直线P1P2没有两点式方程。
x=x1
y=y1
两点式的适用范围:斜率存在且斜率不为0!
当x1=x2时,直线P1P2垂直于x轴,直线方程为x-x1=0,即x=x1;
当y1=y2时,直线P1P2垂直于y轴,直线方程为y-y1=0,即y=y1。
直线的两点式方程具有“对称、整齐”的特征,是直线方程的又一特殊形式;
思考:下列方程是否为过两点P1(x1,y1),P2(x2,y2)的直线方程?能否称为“两点式”?
中点坐标公式:
线段P1P2中P1(x1, y1), P2(x2, y2), 则中点P(x,y) :
重心坐标公式:
在 △ABC中A(x1, y1), B(x2, y2), C(x3, y3), 则重心G(x,y) :
思考:直角坐标平面内的所有直线都可表示为截距式吗?考查下列特殊情形,你能得到什么结论?
(1)直线l垂直于x轴:
(3)直线l经过坐标原点:
(2)直线l垂直于y轴:
x=a
y=b
y=kx
截距式适用范围:直线l与两坐标轴不垂直且不过原点的直线。
回答:若直线l在两坐标轴上的截距相等,则直线l的方程:
x+y=a或y=kx
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(1)三角形三边所在直线的方程;
题型一 直线的两点式方程
解:直线AB:
直线BC:
直线AC:
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(2)BC边上中线AM所在直线的方程;
题型一 直线的两点式方程
M
解:
题型一 直线的两点式方程
例1:已知三角形的三个顶点A(-5, 0),B(3, -3),C(0, 2),求:
(3)BC边垂直平分线l所在直线的方程.
M
解:
注意:当已知两点坐标,求过这两点的直线方程时,首先要判断是否满足两点式方程的适用条件:两点的连线不平行于坐标轴.若满足,则考虑用两点式求方程.
[跟踪训练] 1 (1)过(1,1),(2,-1)两点的直线方程为( )A.2x-y-1=0 B.x-2y+3=0C.2x+y-3=0 D.x+2y-3=0(2) 经过M(3,2)与N(6,2)两点的直线方程为( )A.x=2 B.y=2 C.x=3 D.x=6
题型一 直线的两点式方程
(3)如图,已知A(1,2),B(-1,4),C(5,2).①求线段AB中点D的坐标;②求△ABC的边AB上的中线所在的直线方程.
(3)解 ①线段AB中点D的坐标为D(0,3).②△ABC的边AB上的中线所在的直线方程为
x+5y-15=0.
答案:C
答案:B
题型二 直线的截距式方程
例2 求过点A(3,4),且在两坐标轴上的截距截距相等的直线l的方程。
题型二 直线的截距式方程
注意: (1)如果问题中涉及直线与两坐标轴相交,则可考虑选用直线截距式的方程,用待定系数法确定其系数即可.(2)选用直线截距式的方程时,必须首先考虑直线能否过原点以及能否与两坐标轴垂直.如果题目中出现直线在两坐标轴上的“截距相等”、“截距互为相反数”、“在一坐标轴上的截距是另一坐标轴上截距的m倍(m>0)”等条件时,采用截距式求直线方程,要考虑“零截距”的情况.
[跟踪训练] 2 (1)求过点A(4,2),且在两坐标轴上的截距的绝对值相等的直线l的方程.
题型二 直线的截距式方程
[跟踪训练] 2 (2)已知直线l过点A(1,2),且与两坐标轴的正半轴围成的三角形的面积是4,求直线l的方程.
1.点斜式方程:
y-y0=k(x-x0) (已知定点(x0, y0)及斜率k存在)
2. 斜截式方程:
y=kx+b [已知k存在及截距 b(与y轴交点(0, b)]
3. 两点式方程:
[已知两定点(不适合与x轴或y轴垂直的直线)]
4. 截距式方程:
[已知截距a(与x轴交点(a,0))及截距b(与y轴交点(0, b))不适合过原点的直线]
【当堂达标】
答案:A
答案:A
答案:B
4.已知点A(3,2),B(-1,4),则经过点C(2,5)且经过线段AB的中点的直线方程为________.
5.过点P(1,2)且在两坐标轴上截距的和为0的直线方程为_________ .
6.直线l经过点A(-3,4),且在x轴上的截距是在y轴上的截距的2倍,求该直线的方程.
【当堂达标】
