人教版黑龙江省哈尔滨市2023年秋期(五四学制)七年级期中数学试题01(含解析)
文档属性
| 名称 | 人教版黑龙江省哈尔滨市2023年秋期(五四学制)七年级期中数学试题01(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 00:00:00 | ||
图片预览


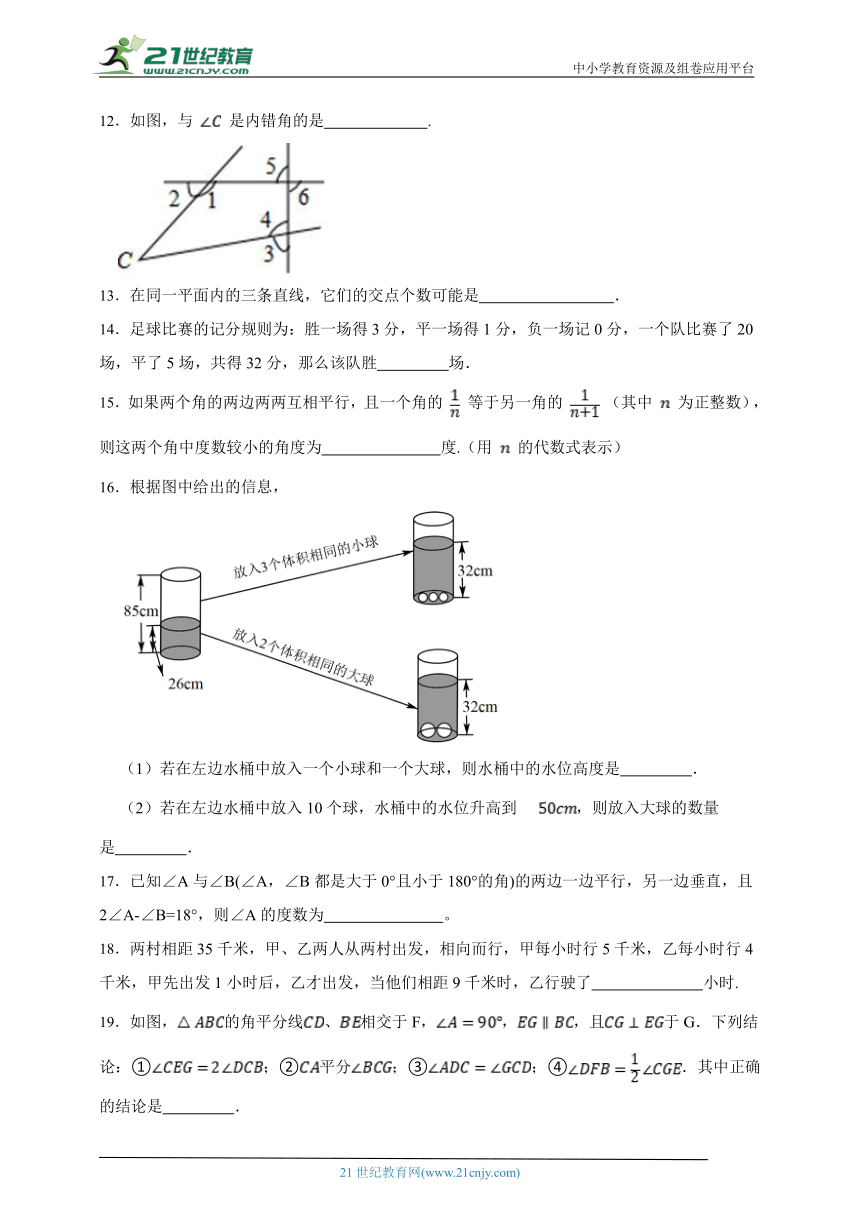
文档简介
中小学教育资源及组卷应用平台
黑龙江省哈尔滨市2023年秋期人教版(五四学制)数学
七年级期中试题01
120分钟 120分
一、单选题 30分,每题3分
1.下列句子中是命题且是真命题的是( )
A.同位角相等 B.直线AB垂直CD吗
C.若a2=b2,则a=b D.同角的补角相等
2.如图所示,ACD相交于点O,OE⊥AB,那么下列结论错误的是 ( )
A.∠AOC与∠COE互为余角 B.∠BOD与∠COE互为余角
C.∠COE与∠BOE互为补角 D.∠AOC与∠BOD是对顶角
3.下列方程属于一元一次方程的是( )
A. ﹣1=0 B.3m=2 C.6x+1=3y D.2y2﹣4y+1=0
4.下列方程中,属于一元一次方程的是( )
A. B. C. D.
5.如图,若m∥n,∠1=105 o,则∠2=( )
A.55 o B.60 o C.65 o D.75 o
6.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
7.如图,直线 , 分别是 的平分线,则 与 的和一定是( )
A. B. C. D.
8.新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩面和口罩耳绳刚好配套,设安排名工人生产口罩面,则下面所列方程正确的是( )
A. B.
C. D.
9.如图,下列条件中,不能判定 的是( )
A. B.
C. D.
10.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④
C.①③④ D.①②③④ 图4
二、填空题 30分,每题3分
11.若x=2是方程k(x-3)=1的解,则k= .
12.如图,与 是内错角的是 .
13.在同一平面内的三条直线,它们的交点个数可能是 .
14.足球比赛的记分规则为:胜一场得3分,平一场得1分,负一场记0分,一个队比赛了20场,平了5场,共得32分,那么该队胜 场.
15.如果两个角的两边两两互相平行,且一个角的 等于另一角的 (其中 为正整数),则这两个角中度数较小的角度为 度.(用 的代数式表示)
16.根据图中给出的信息,
(1)若在左边水桶中放入一个小球和一个大球,则水桶中的水位高度是 .
(2)若在左边水桶中放入10个球,水桶中的水位升高到,则放入大球的数量是 .
17.已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A-∠B=18°,则∠A的度数为 。
18.两村相距35千米,甲、乙两人从两村出发,相向而行,甲每小时行5千米,乙每小时行4千米,甲先出发1小时后,乙才出发,当他们相距9千米时,乙行驶了 小时.
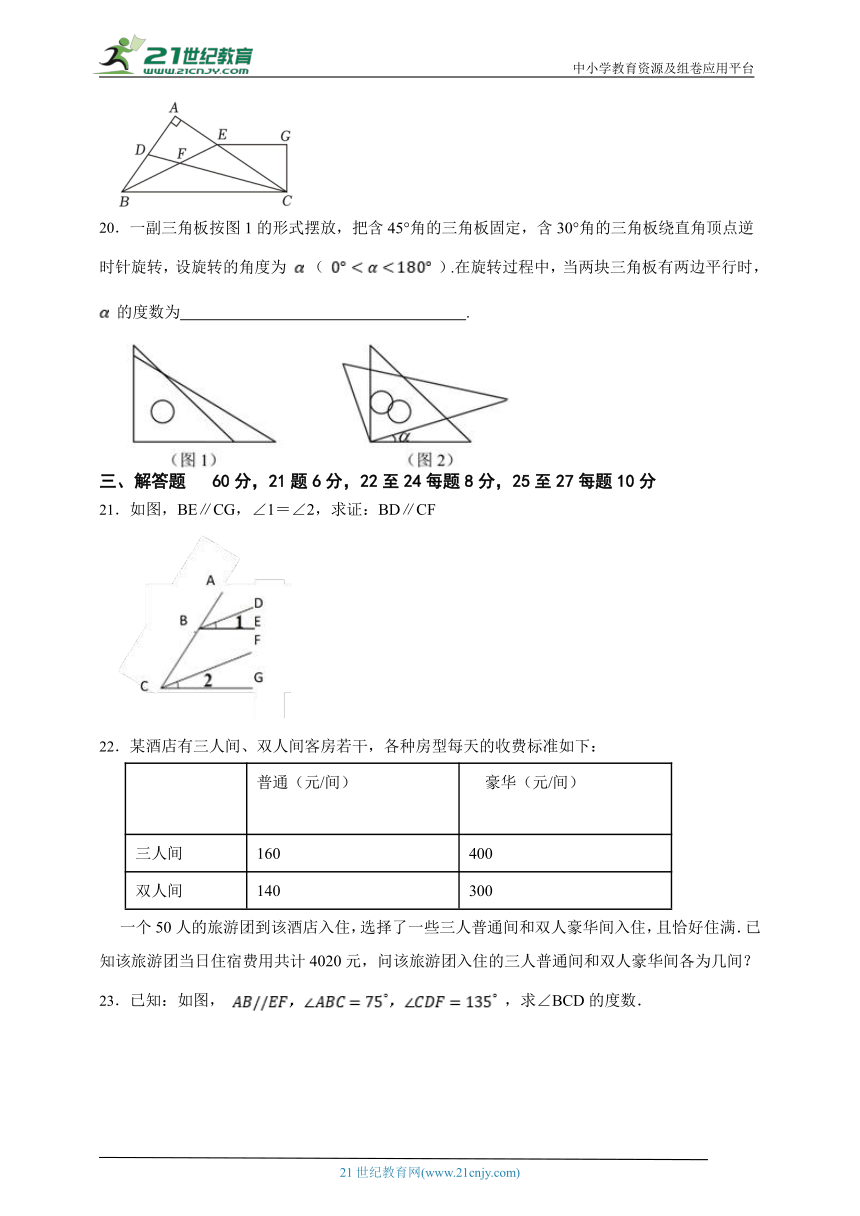
19.如图,的角平分线、相交于F,,,且于G.下列结论:①;②平分;③;④.其中正确的结论是 .
20.一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为 ( ).在旋转过程中,当两块三角板有两边平行时, 的度数为 .
三、解答题 60分,21题6分,22至24每题8分,25至27每题10分
21.如图,BE∥CG,∠1=∠2,求证:BD∥CF
22.某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) 豪华(元/间)
三人间 160 400
双人间 140 300
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
23.已知:如图, ,求∠BCD的度数.
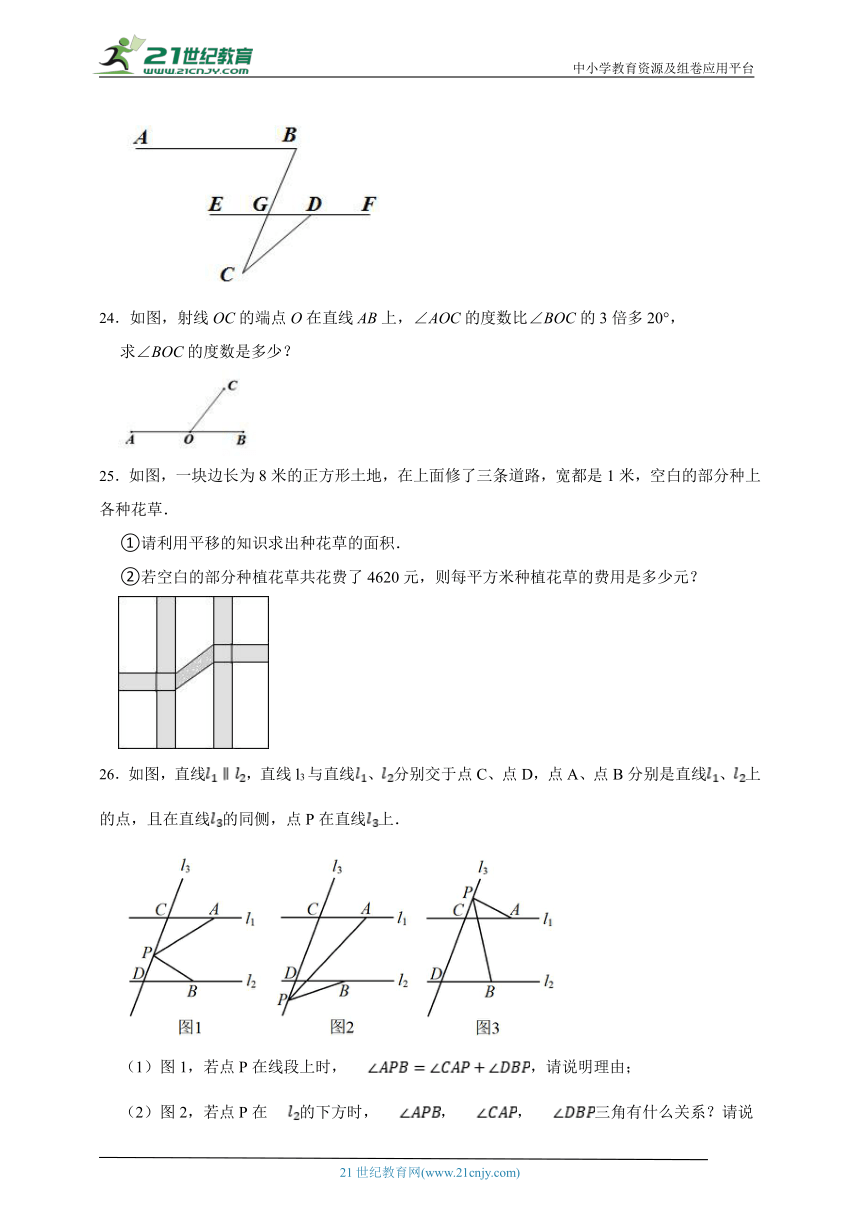
24.如图,射线OC的端点O在直线AB上,∠AOC的度数比∠BOC的3倍多20°,
求∠BOC的度数是多少?
25.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
①请利用平移的知识求出种花草的面积.
②若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
26.如图,直线,直线l3与直线、分别交于点C、点D,点A、点B分别是直线、上的点,且在直线的同侧,点P在直线上.
(1)图1,若点P在线段上时,,请说明理由;
(2)图2,若点P在的下方时,,,三角有什么关系?请说明理由;
(3)图3,若点P在直线的上方时,请直接写出,,三角的关系.
27.家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
( 1 )他下山时的速度比上山时的速度每小时快1千米;
( 2 )他上山2小时到达的位置,离山顶还有1千米;
( 3 )抄近路下山,下山路程比上山路程近2千米;
( 4 )下山用1个小时;
根据上面信息,他作出如下计划:
( 1 )在山顶游览1个小时;
( 2 )中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
答案解析部分
1.【答案】D
【解析】【解答】A.同位角相等是假命题,故不符合题意;
B.直线AB垂直CD吗是问句,不是命题;
C.若a2=b2,则a=b假命题,故不符合题意;
D.同角的补角相等是证明题;
故答案为:D.
【分析】根据真命题的定义逐项判断即可。
2.【答案】C
【解析】【分析】利用互余、互补以及对顶角的定义逐一判断.
【解答】A、∵OE⊥AB,则∠AOE=90°,即∠AOC+∠COE=90°,正确;
B、∵OE⊥AB,则∠BOE=90°,而∠BOD+∠BOE+∠COE=180°,
∴∠BOD+∠COE=90°,正确;
C、∵OE⊥AB,则∠BOE=90°,而∠COE为锐角,∠BOE+∠COE<180°,错误;
D、∠AOC与∠BOD是对顶角,正确.
故选C.
【点评】本题主要考查互余、互补以及对顶角的定义,是对基本概念的考查,难度不大.
3.【答案】B
【解析】【解答】A.含有分式.故错误.
B.正确.
C.含有两个未知数.故错误.
D.未知数的最高次数是2.故错误.
故答案为:B.
【分析】根据一元一次方程的定义,只含有一个未知数,并且未知数的最高次数是1的整式方程,来判断即可。
4.【答案】C
【解析】【解答】A、 +y=2,是分式方程,故不符合题意;
B、2x+y=6,是二元一次方程,故不符合题意;
C、x=1是一元一次方程,故符合题意;
D、x2﹣1=3是一元二次方程,故不符合题意.
故答案为:C.
【分析】根据一元一次方程的定义“只含有一个未知数、且未知数的最高次数是1的整式方程叫作一元一次方程”即可判断求解.
5.【答案】D
【解析】【解答】解:∵m∥n,∴∠1+∠2=180°,又∠1=105°,∴∠2=75°.
故答案为:D.
【分析】两直线平行,同旁内角互补,得到∠1+∠2=180°.
6.【答案】C
【解析】【解答】解:根据对顶角的定义(具有共同顶点,两边互为反向延长线的两个角互为对顶角),观察四个选项,只有选项C符合题意.
故答案为:C.
【分析】根据对顶角的定义求解即可。
7.【答案】A
【解析】【解答】解:∵AC∥BD,
∴∠CAB+∠ABD=180°,
∵AO、BO分别是∠BAC、∠ABD的平分线,
∴∠CAB=2∠BAO,∠ABD=2∠ABO,
∴∠BAO+∠ABO=90°,
故答案为:A.
【分析】根据平行线的性质得出∠CAB+∠ABD=180°,再根据角平分线的定义得出结论.
8.【答案】C
【解析】【解答】解:设安排x名工人生产口罩面,则(26-x)人生产耳绳,由题意得
1000(26-x)=2×800x.
故答案为:C.
【分析】设安排x名工人生产口罩面,则(26-x)人生产耳绳,根据题意直接列出方程1000(26-x)=2×800x即可。
9.【答案】C
【解析】【解答】解: 、 ,根据同旁内角互补,两直线平行,可得 ∥ ,故 不符合题意;
、 ,根据内错角相等,两直线平行,可得 ∥ ,故 不符合题意;
、 ,根据内错角相等,两直线平行,可得 ∥ ,故 符合题意;;
、 ,根据同位角相等,两直线平行,可得 ∥ ,故 不符合题意.
故答案为: .
【分析】利用同旁内角互补,两直线平行,由∠D+∠BAD=180°,可证得AB∥CD,可对A作出判断;利用内错角相等,两直线平行,由B选项中的条件,可证得AB∥CD;由C选项中的条件,可证得AD∥BC;利用同位角相等,两直线平行,由D选项中的条件,可证得AB∥CD,由此可得不能判断AB∥CD的选项.
10.【答案】D
【解析】【解答】解:如下图,当E点在直线AB,CD之间并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠AEF+∠FEC=α+β
故①正确
如下图,当E点在直线AB上面并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠FEC-∠AEF=β-α
故③正确
如下图,当E点在直线CD下面并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠AEF-∠FEC=α-β
故②正确
如下图,当E点在直线AB,CD之间并且在AC左边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE+∠AEF=180° 、∠DCE+∠FEC=180°
∴∠AEC=∠AEF+∠FEC=180° -α+180°-β=360°﹣α﹣β
故④正确
∴①②③④正确
故答案为:D
【分析】本题考查了平行线间的动点问题,直线AB,CD,AC将平面分成了6个部分,E点可以在任意部分,再根据平行线的性质以及角度的加减即可得到答案.
11.【答案】-1
【解析】【解答】解:∵x=2是方程k(x-3)=1的解,∴ - k=1,解得k= -1,故答案为: 1.
【分析】把x=2代入方程k(x-3)=1即可解得k的值.
12.【答案】∠2,∠3
【解析】【解答】解:如图所示,与∠C是内错角的是∠2,∠3;
故答案为:∠2,∠3.
【分析】两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角,据此判断.
13.【答案】0或1或2或3个
【解析】【解答】解:如图,
由图可知:同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案是:0或1或2或3个.
【分析】画出三条线所有的可能情况即可得到答案。
14.【答案】9
【解析】【解答】解:设该队胜x场,依题意得:3x+5=32
解得:x=9
故答案为:9.
【分析】设该队胜x场,根据记分规则和得分总数,可列方程3x+5=32求解.
15.【答案】
【解析】【解答】解:设其中一个角是x,则另一个角是180-x,根据题意,得
解得 ,
故答案为: .
【分析】设其中一个角是x,得出另一个角是180-x,根据题意列出方程,解方程求出x的值,即可得出答案.
16.【答案】(1)31cm
(2)4个
【解析】【解答】解:(1)由已知得,在左边水桶中放入一个小球水桶中的水位高度上升 (cm),放入一个大球水桶中的水位高度上升(cm),
∴在左边水桶中放入一个小球和一个大球,水桶中的水位高度是26+2+3=31(cm),
故答案为:31cm;
(2)设放入大球x个,则放入小球(10 x)个,
根据题意得:3x+2(10 x)=50 26,
解得x=4,
答:放入大球4个,
故答案为:4个.
【分析】(1)由已知得出放入一个小球水位高度上升,(cm),放入一个大球水桶中的水位高度上升(cm);
(2)设放入大球x个,则放入小球(10 x)个,根据题意列出方程即可得解。
17.【答案】36°或96°
【解析】【解答】解:1)如图,当C为凸点时,过C作CF∥AD,则CF∥AD,
∴∠B+∠BCF=180°,∠ACF+∠A=180°,
即∠B+∠BCF+∠ACF+∠A=360°,
∵∠BCF+∠ACF=90°,
∴∠A+∠B=270°,
∵2∠A-∠B=18°
∴∠A+∠B+2∠A-∠B=270°+18°,
∴3∠A=288°,
∴∠A=96°
2)如图,当C为凹点时,过C作CF∥AD,则CF∥AD,
∴∠B=∠BCF,∠ACF=∠A,
∴∠B+∠A=∠BCF+∠ACF=90°,
∵2∠A-∠B=18° ,
∴∠B+∠A+2∠A-∠B=90°+18°,
∵3∠A=108° ,
∴∠A=36°。
故答案为: 36°或96°.
【分析】本题分两种情况讨论,当C凸点或当C为凹点时,两种情况都是过C作BE的平行线,由平行线的性质定理得到,∠A和∠B之和为270°,或∠A和∠B之和为90°,再结合已知 2∠A-∠B=18°,组成方程组求解即可。
18.【答案】 或
【解析】【解答】解:由题意,分以下两种情况:
①当甲、乙两人相遇前,相距9千米时,
设乙行驶了 小时,
则 ,
解得 (小时);
②当甲、乙两人相遇后,相距9千米时,
设乙行驶了 小时,
则 ,
解得 (小时);
综上,当他们相距9千米时,乙行驶了 或 小时,
故答案为: 或 .
【分析】根据题意分①当甲、乙两人相遇前,相距9千米时;②当甲、乙两人相遇后,相距9千米时两种情况,根据行程问题的等量关系分别列方程,然后求出方程的解.
19.【答案】①③④
【解析】【解答】 解:①∵ ,
,
又 是 的角平分线,
,故①正确;
②无法证明 平分 ,故②错误;
③ ,
,
平分 ,
,
.
∵ ,且 ,
,即 ,
,故③正确;
④ , ,
,
,
,故④正确.
故答案为:①③④.
【分析】利用角平分线的定义,平行线的性质及角的运算和等量代换逐项判断即可.
20.【答案】30°或45°或120°或135°或165°
【解析】【解答】解:①当CD∥OB时,∠α=∠D=30°
②当OC∥AB时,∠OEB=∠COD=90°,此时∠α=90°-∠B=90°-45°=45°
③当DC∥OA时,∠DOA=∠D=30°,此时∠α=∠AOB+∠AOD=90°+30°=120°
④当OD∥AB时,∠AOD=∠A=45°,此时∠α=∠A+∠AOD=90°+45°=135°
⑤当CD∥AB时,延长BO交CD于点E,则∠CEO=∠B=45°
∴∠DEO=180°-∠CEO=135°
∴∠DOE=180°-∠DEO-∠D=15°
此时∠α=180°-∠DOE=180°-15°=165°
综上,在旋转过程中,当两块三角板有两边平行时, 的度数为30°或45°或120°或135°或165°.
故答案为:30°或45°或120°或135°或165°.
【分析】利用旋转过程中,两边平行分类讨论:①当CD∥OB时,利用“两直线平行,内错角相等”求解;②当OC∥AB时,先利用“两直线平行,内错角相等”,求∠OEB=90°,再利用“三角形内角和180°”,求解;③当DC∥OA时,先利用“两直线平行,内错角相等”求∠DOA=30°,再求∠α=120°;④当OD∥AB时,先用“两直线平行,内错角相等”求∠AOD=45°,再求∠α=135°;⑤当CD∥AB时,延长BO交CD于点E,利用“两直线平行,内错角相等”求则∠CEO=45°,再利用平角求∠DEO=135°,再利用“三角形内角和180°”求∠DOE=15°,最后求∠α=165°.
21.【答案】证明:∵BE∥CG,
∴∠ABE=∠ACG,
∵∠1=∠2,
∴∠ABD=∠ACF,
∴BD∥CF.
【解析】【分析】只要证明∠ABD=∠ACF,根据同位角相等两直线平行即可证明.
22.【答案】解:设该旅游团入住的三人普通间数为x,则入住双人豪华间数为 .
根据题意,得 160x+300× =4020.
解得:x=12.
从而 =7.
答:该旅游团入住三人普通间12间、双人豪华间7间.
【解析】【分析】设该旅游团入住的三人普通间数为x,则入住双人豪华间数为 ,由住普通三人间的费用+住豪华双人间的费用=4020得出方程,求解即可。
23.【答案】解:∵AB∥EF,∠ABC=75°,
∴∠EGC=∠ABC=75°.
∵∠CDF=135°,
∴∠EDC=180°-∠CDF=180°-135°=45°.
又∵∠EGC=∠BCD+∠EDC,
∴∠BCD=75°-45°=30°.
【解析】【分析】先求出 ∠EGC=∠ABC=75°,再求出∠EDC= 45°,最后计算求解即可。
24.【答案】解:
则
【解析】【分析】设∠BOC=x,根据题意得出∠AOC=3x+20,利用平角=180°列出方程,解方程求出x的值,即可得出答案.
25.【答案】【解答】①(8-2)×(8-1)
=6×7=42(米2)
答:种花草的面积为42米2.
②4620÷42=110(元)
答:每平方米种植花草的费用是110元.
【解析】【分析】①将道路直接平移到矩形的边上进而得出答案;②根据①中所求即可得出答案.
26.【答案】(1)解:过点P作
∴
又∵
∴
∴
∵
∴
(2)解:,理由:
过点P作
∴
又∵
∴
∴
∵
∴
(3)解:,理由:
过点P作
∴
∵
∴
∴
又∵
∴
∴
∵
∴
【解析】【分析】(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
27.【答案】解:设上山的速度为v,下山的速度为(v+1),则 2v+1=v+1+2, 解得 v=2. 即上山速度是2千米/小时. 则下山的速度是3千米/小时,山高为5千米. 则计划上山的时间为:5÷2=2.5(小时), 计划下山的时间为:1小时, 则共用时间为:2.5+1+1=4.5(小时), 所以出发时间为:12:00﹣4小时30分钟=7:30. 答:孔明同学应该在7点30分从家出发.
【解析】【分析】根据题中提供的信息可知: 设上山的速度为v,由(1)可求出下山的速度,由(2)可得出S=2v+1,再由(3)(4)建立方程求出v的值,然后分别求出上下山的时间,就可求出一共需的时间,即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
黑龙江省哈尔滨市2023年秋期人教版(五四学制)数学
七年级期中试题01
120分钟 120分
一、单选题 30分,每题3分
1.下列句子中是命题且是真命题的是( )
A.同位角相等 B.直线AB垂直CD吗
C.若a2=b2,则a=b D.同角的补角相等
2.如图所示,ACD相交于点O,OE⊥AB,那么下列结论错误的是 ( )
A.∠AOC与∠COE互为余角 B.∠BOD与∠COE互为余角
C.∠COE与∠BOE互为补角 D.∠AOC与∠BOD是对顶角
3.下列方程属于一元一次方程的是( )
A. ﹣1=0 B.3m=2 C.6x+1=3y D.2y2﹣4y+1=0
4.下列方程中,属于一元一次方程的是( )
A. B. C. D.
5.如图,若m∥n,∠1=105 o,则∠2=( )
A.55 o B.60 o C.65 o D.75 o
6.下列各图中,∠1与∠2是对顶角的是( )
A. B.
C. D.
7.如图,直线 , 分别是 的平分线,则 与 的和一定是( )
A. B. C. D.
8.新型冠状肺炎疫情正在全球蔓延肆虐,口罩成了人们生活中必不可少的物品,某口罩厂有26名工人,每人每天可以生产800个口罩面或1000个口罩耳绳.一个口罩面需要配两个耳绳,为使每天生产的口罩面和口罩耳绳刚好配套,设安排名工人生产口罩面,则下面所列方程正确的是( )
A. B.
C. D.
9.如图,下列条件中,不能判定 的是( )
A. B.
C. D.
10.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:
①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④
C.①③④ D.①②③④ 图4
二、填空题 30分,每题3分
11.若x=2是方程k(x-3)=1的解,则k= .
12.如图,与 是内错角的是 .
13.在同一平面内的三条直线,它们的交点个数可能是 .
14.足球比赛的记分规则为:胜一场得3分,平一场得1分,负一场记0分,一个队比赛了20场,平了5场,共得32分,那么该队胜 场.
15.如果两个角的两边两两互相平行,且一个角的 等于另一角的 (其中 为正整数),则这两个角中度数较小的角度为 度.(用 的代数式表示)
16.根据图中给出的信息,
(1)若在左边水桶中放入一个小球和一个大球,则水桶中的水位高度是 .
(2)若在左边水桶中放入10个球,水桶中的水位升高到,则放入大球的数量是 .
17.已知∠A与∠B(∠A,∠B都是大于0°且小于180°的角)的两边一边平行,另一边垂直,且2∠A-∠B=18°,则∠A的度数为 。
18.两村相距35千米,甲、乙两人从两村出发,相向而行,甲每小时行5千米,乙每小时行4千米,甲先出发1小时后,乙才出发,当他们相距9千米时,乙行驶了 小时.
19.如图,的角平分线、相交于F,,,且于G.下列结论:①;②平分;③;④.其中正确的结论是 .
20.一副三角板按图1的形式摆放,把含45°角的三角板固定,含30°角的三角板绕直角顶点逆时针旋转,设旋转的角度为 ( ).在旋转过程中,当两块三角板有两边平行时, 的度数为 .
三、解答题 60分,21题6分,22至24每题8分,25至27每题10分
21.如图,BE∥CG,∠1=∠2,求证:BD∥CF
22.某酒店有三人间、双人间客房若干,各种房型每天的收费标准如下:
普通(元/间) 豪华(元/间)
三人间 160 400
双人间 140 300
一个50人的旅游团到该酒店入住,选择了一些三人普通间和双人豪华间入住,且恰好住满.已知该旅游团当日住宿费用共计4020元,问该旅游团入住的三人普通间和双人豪华间各为几间?
23.已知:如图, ,求∠BCD的度数.
24.如图,射线OC的端点O在直线AB上,∠AOC的度数比∠BOC的3倍多20°,
求∠BOC的度数是多少?
25.如图,一块边长为8米的正方形土地,在上面修了三条道路,宽都是1米,空白的部分种上各种花草.
①请利用平移的知识求出种花草的面积.
②若空白的部分种植花草共花费了4620元,则每平方米种植花草的费用是多少元?
26.如图,直线,直线l3与直线、分别交于点C、点D,点A、点B分别是直线、上的点,且在直线的同侧,点P在直线上.
(1)图1,若点P在线段上时,,请说明理由;
(2)图2,若点P在的下方时,,,三角有什么关系?请说明理由;
(3)图3,若点P在直线的上方时,请直接写出,,三角的关系.
27.家住山脚下的孔明同学想从家出发登山游玩,据以往的经验,他获得如下信息:
( 1 )他下山时的速度比上山时的速度每小时快1千米;
( 2 )他上山2小时到达的位置,离山顶还有1千米;
( 3 )抄近路下山,下山路程比上山路程近2千米;
( 4 )下山用1个小时;
根据上面信息,他作出如下计划:
( 1 )在山顶游览1个小时;
( 2 )中午12:00回到家吃中餐.
若依据以上信息和计划登山游玩,请问:孔明同学应该在什么时间从家出发?
答案解析部分
1.【答案】D
【解析】【解答】A.同位角相等是假命题,故不符合题意;
B.直线AB垂直CD吗是问句,不是命题;
C.若a2=b2,则a=b假命题,故不符合题意;
D.同角的补角相等是证明题;
故答案为:D.
【分析】根据真命题的定义逐项判断即可。
2.【答案】C
【解析】【分析】利用互余、互补以及对顶角的定义逐一判断.
【解答】A、∵OE⊥AB,则∠AOE=90°,即∠AOC+∠COE=90°,正确;
B、∵OE⊥AB,则∠BOE=90°,而∠BOD+∠BOE+∠COE=180°,
∴∠BOD+∠COE=90°,正确;
C、∵OE⊥AB,则∠BOE=90°,而∠COE为锐角,∠BOE+∠COE<180°,错误;
D、∠AOC与∠BOD是对顶角,正确.
故选C.
【点评】本题主要考查互余、互补以及对顶角的定义,是对基本概念的考查,难度不大.
3.【答案】B
【解析】【解答】A.含有分式.故错误.
B.正确.
C.含有两个未知数.故错误.
D.未知数的最高次数是2.故错误.
故答案为:B.
【分析】根据一元一次方程的定义,只含有一个未知数,并且未知数的最高次数是1的整式方程,来判断即可。
4.【答案】C
【解析】【解答】A、 +y=2,是分式方程,故不符合题意;
B、2x+y=6,是二元一次方程,故不符合题意;
C、x=1是一元一次方程,故符合题意;
D、x2﹣1=3是一元二次方程,故不符合题意.
故答案为:C.
【分析】根据一元一次方程的定义“只含有一个未知数、且未知数的最高次数是1的整式方程叫作一元一次方程”即可判断求解.
5.【答案】D
【解析】【解答】解:∵m∥n,∴∠1+∠2=180°,又∠1=105°,∴∠2=75°.
故答案为:D.
【分析】两直线平行,同旁内角互补,得到∠1+∠2=180°.
6.【答案】C
【解析】【解答】解:根据对顶角的定义(具有共同顶点,两边互为反向延长线的两个角互为对顶角),观察四个选项,只有选项C符合题意.
故答案为:C.
【分析】根据对顶角的定义求解即可。
7.【答案】A
【解析】【解答】解:∵AC∥BD,
∴∠CAB+∠ABD=180°,
∵AO、BO分别是∠BAC、∠ABD的平分线,
∴∠CAB=2∠BAO,∠ABD=2∠ABO,
∴∠BAO+∠ABO=90°,
故答案为:A.
【分析】根据平行线的性质得出∠CAB+∠ABD=180°,再根据角平分线的定义得出结论.
8.【答案】C
【解析】【解答】解:设安排x名工人生产口罩面,则(26-x)人生产耳绳,由题意得
1000(26-x)=2×800x.
故答案为:C.
【分析】设安排x名工人生产口罩面,则(26-x)人生产耳绳,根据题意直接列出方程1000(26-x)=2×800x即可。
9.【答案】C
【解析】【解答】解: 、 ,根据同旁内角互补,两直线平行,可得 ∥ ,故 不符合题意;
、 ,根据内错角相等,两直线平行,可得 ∥ ,故 不符合题意;
、 ,根据内错角相等,两直线平行,可得 ∥ ,故 符合题意;;
、 ,根据同位角相等,两直线平行,可得 ∥ ,故 不符合题意.
故答案为: .
【分析】利用同旁内角互补,两直线平行,由∠D+∠BAD=180°,可证得AB∥CD,可对A作出判断;利用内错角相等,两直线平行,由B选项中的条件,可证得AB∥CD;由C选项中的条件,可证得AD∥BC;利用同位角相等,两直线平行,由D选项中的条件,可证得AB∥CD,由此可得不能判断AB∥CD的选项.
10.【答案】D
【解析】【解答】解:如下图,当E点在直线AB,CD之间并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠AEF+∠FEC=α+β
故①正确
如下图,当E点在直线AB上面并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠FEC-∠AEF=β-α
故③正确
如下图,当E点在直线CD下面并且在AC右边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE=∠AEF 、∠DCE=∠FEC
∴∠AEC=∠AEF-∠FEC=α-β
故②正确
如下图,当E点在直线AB,CD之间并且在AC左边时,作EF//AB
∵AB∥CD、EF//AB
∴AB∥CD∥EF
∴∠BAE+∠AEF=180° 、∠DCE+∠FEC=180°
∴∠AEC=∠AEF+∠FEC=180° -α+180°-β=360°﹣α﹣β
故④正确
∴①②③④正确
故答案为:D
【分析】本题考查了平行线间的动点问题,直线AB,CD,AC将平面分成了6个部分,E点可以在任意部分,再根据平行线的性质以及角度的加减即可得到答案.
11.【答案】-1
【解析】【解答】解:∵x=2是方程k(x-3)=1的解,∴ - k=1,解得k= -1,故答案为: 1.
【分析】把x=2代入方程k(x-3)=1即可解得k的值.
12.【答案】∠2,∠3
【解析】【解答】解:如图所示,与∠C是内错角的是∠2,∠3;
故答案为:∠2,∠3.
【分析】两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角,据此判断.
13.【答案】0或1或2或3个
【解析】【解答】解:如图,
由图可知:同一平面内的三条直线,其交点个数为:0个;1个;2个;3个.
故答案是:0或1或2或3个.
【分析】画出三条线所有的可能情况即可得到答案。
14.【答案】9
【解析】【解答】解:设该队胜x场,依题意得:3x+5=32
解得:x=9
故答案为:9.
【分析】设该队胜x场,根据记分规则和得分总数,可列方程3x+5=32求解.
15.【答案】
【解析】【解答】解:设其中一个角是x,则另一个角是180-x,根据题意,得
解得 ,
故答案为: .
【分析】设其中一个角是x,得出另一个角是180-x,根据题意列出方程,解方程求出x的值,即可得出答案.
16.【答案】(1)31cm
(2)4个
【解析】【解答】解:(1)由已知得,在左边水桶中放入一个小球水桶中的水位高度上升 (cm),放入一个大球水桶中的水位高度上升(cm),
∴在左边水桶中放入一个小球和一个大球,水桶中的水位高度是26+2+3=31(cm),
故答案为:31cm;
(2)设放入大球x个,则放入小球(10 x)个,
根据题意得:3x+2(10 x)=50 26,
解得x=4,
答:放入大球4个,
故答案为:4个.
【分析】(1)由已知得出放入一个小球水位高度上升,(cm),放入一个大球水桶中的水位高度上升(cm);
(2)设放入大球x个,则放入小球(10 x)个,根据题意列出方程即可得解。
17.【答案】36°或96°
【解析】【解答】解:1)如图,当C为凸点时,过C作CF∥AD,则CF∥AD,
∴∠B+∠BCF=180°,∠ACF+∠A=180°,
即∠B+∠BCF+∠ACF+∠A=360°,
∵∠BCF+∠ACF=90°,
∴∠A+∠B=270°,
∵2∠A-∠B=18°
∴∠A+∠B+2∠A-∠B=270°+18°,
∴3∠A=288°,
∴∠A=96°
2)如图,当C为凹点时,过C作CF∥AD,则CF∥AD,
∴∠B=∠BCF,∠ACF=∠A,
∴∠B+∠A=∠BCF+∠ACF=90°,
∵2∠A-∠B=18° ,
∴∠B+∠A+2∠A-∠B=90°+18°,
∵3∠A=108° ,
∴∠A=36°。
故答案为: 36°或96°.
【分析】本题分两种情况讨论,当C凸点或当C为凹点时,两种情况都是过C作BE的平行线,由平行线的性质定理得到,∠A和∠B之和为270°,或∠A和∠B之和为90°,再结合已知 2∠A-∠B=18°,组成方程组求解即可。
18.【答案】 或
【解析】【解答】解:由题意,分以下两种情况:
①当甲、乙两人相遇前,相距9千米时,
设乙行驶了 小时,
则 ,
解得 (小时);
②当甲、乙两人相遇后,相距9千米时,
设乙行驶了 小时,
则 ,
解得 (小时);
综上,当他们相距9千米时,乙行驶了 或 小时,
故答案为: 或 .
【分析】根据题意分①当甲、乙两人相遇前,相距9千米时;②当甲、乙两人相遇后,相距9千米时两种情况,根据行程问题的等量关系分别列方程,然后求出方程的解.
19.【答案】①③④
【解析】【解答】 解:①∵ ,
,
又 是 的角平分线,
,故①正确;
②无法证明 平分 ,故②错误;
③ ,
,
平分 ,
,
.
∵ ,且 ,
,即 ,
,故③正确;
④ , ,
,
,
,故④正确.
故答案为:①③④.
【分析】利用角平分线的定义,平行线的性质及角的运算和等量代换逐项判断即可.
20.【答案】30°或45°或120°或135°或165°
【解析】【解答】解:①当CD∥OB时,∠α=∠D=30°
②当OC∥AB时,∠OEB=∠COD=90°,此时∠α=90°-∠B=90°-45°=45°
③当DC∥OA时,∠DOA=∠D=30°,此时∠α=∠AOB+∠AOD=90°+30°=120°
④当OD∥AB时,∠AOD=∠A=45°,此时∠α=∠A+∠AOD=90°+45°=135°
⑤当CD∥AB时,延长BO交CD于点E,则∠CEO=∠B=45°
∴∠DEO=180°-∠CEO=135°
∴∠DOE=180°-∠DEO-∠D=15°
此时∠α=180°-∠DOE=180°-15°=165°
综上,在旋转过程中,当两块三角板有两边平行时, 的度数为30°或45°或120°或135°或165°.
故答案为:30°或45°或120°或135°或165°.
【分析】利用旋转过程中,两边平行分类讨论:①当CD∥OB时,利用“两直线平行,内错角相等”求解;②当OC∥AB时,先利用“两直线平行,内错角相等”,求∠OEB=90°,再利用“三角形内角和180°”,求解;③当DC∥OA时,先利用“两直线平行,内错角相等”求∠DOA=30°,再求∠α=120°;④当OD∥AB时,先用“两直线平行,内错角相等”求∠AOD=45°,再求∠α=135°;⑤当CD∥AB时,延长BO交CD于点E,利用“两直线平行,内错角相等”求则∠CEO=45°,再利用平角求∠DEO=135°,再利用“三角形内角和180°”求∠DOE=15°,最后求∠α=165°.
21.【答案】证明:∵BE∥CG,
∴∠ABE=∠ACG,
∵∠1=∠2,
∴∠ABD=∠ACF,
∴BD∥CF.
【解析】【分析】只要证明∠ABD=∠ACF,根据同位角相等两直线平行即可证明.
22.【答案】解:设该旅游团入住的三人普通间数为x,则入住双人豪华间数为 .
根据题意,得 160x+300× =4020.
解得:x=12.
从而 =7.
答:该旅游团入住三人普通间12间、双人豪华间7间.
【解析】【分析】设该旅游团入住的三人普通间数为x,则入住双人豪华间数为 ,由住普通三人间的费用+住豪华双人间的费用=4020得出方程,求解即可。
23.【答案】解:∵AB∥EF,∠ABC=75°,
∴∠EGC=∠ABC=75°.
∵∠CDF=135°,
∴∠EDC=180°-∠CDF=180°-135°=45°.
又∵∠EGC=∠BCD+∠EDC,
∴∠BCD=75°-45°=30°.
【解析】【分析】先求出 ∠EGC=∠ABC=75°,再求出∠EDC= 45°,最后计算求解即可。
24.【答案】解:
则
【解析】【分析】设∠BOC=x,根据题意得出∠AOC=3x+20,利用平角=180°列出方程,解方程求出x的值,即可得出答案.
25.【答案】【解答】①(8-2)×(8-1)
=6×7=42(米2)
答:种花草的面积为42米2.
②4620÷42=110(元)
答:每平方米种植花草的费用是110元.
【解析】【分析】①将道路直接平移到矩形的边上进而得出答案;②根据①中所求即可得出答案.
26.【答案】(1)解:过点P作
∴
又∵
∴
∴
∵
∴
(2)解:,理由:
过点P作
∴
又∵
∴
∴
∵
∴
(3)解:,理由:
过点P作
∴
∵
∴
∴
又∵
∴
∴
∵
∴
【解析】【分析】(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
(1)过点P作PM∥l1,由平行线的性质得∠APM=∠CAP,根据平行于同一直线的两直线平行得PM∥l2,由平行线的性质得∠BPM=∠DBP,即可得解.
27.【答案】解:设上山的速度为v,下山的速度为(v+1),则 2v+1=v+1+2, 解得 v=2. 即上山速度是2千米/小时. 则下山的速度是3千米/小时,山高为5千米. 则计划上山的时间为:5÷2=2.5(小时), 计划下山的时间为:1小时, 则共用时间为:2.5+1+1=4.5(小时), 所以出发时间为:12:00﹣4小时30分钟=7:30. 答:孔明同学应该在7点30分从家出发.
【解析】【分析】根据题中提供的信息可知: 设上山的速度为v,由(1)可求出下山的速度,由(2)可得出S=2v+1,再由(3)(4)建立方程求出v的值,然后分别求出上下山的时间,就可求出一共需的时间,即可求解。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
