24.3正多边形和圆课堂提升练(含答案)-人教版数学九年级上册
文档属性
| 名称 | 24.3正多边形和圆课堂提升练(含答案)-人教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 20:16:32 | ||
图片预览

文档简介
24.3正多边形和圆课堂提升练-人教版数学九年级上册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一个圆内接正多边形的内角是,则这个多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
2.下列命题错误的是( )
A.圆是轴对称图形 B.各边相等的圆内接多边形是正多边形
C.三角形的内心到它三边的距离相等 D.各角相等的圆内接多边形是正多边形
3.一个圆的内接正多边形中,一条边所对的圆心角为,则该正多边形的边数是( )
A.3 B.4 C.5 D.6
4.如果一个正多边形的中心角为,那么这个正多边形的边数是( ).
A. B. C. D.
5.下列命题是假命题的是( )
A.正五边形的内角和为540°
B.矩形的对角线相等
C.圆内接四边形的对角互补
D.对角线互相垂直的四边形是菱形
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=130°,则∠BOD等于( )
A.90° B.100° C.120° D.130°
7.用尺规作某种六边形的方法,其步骤是:如图,①在上任取一点A,连接并延长交于点B;②以点B为圆心,为半径作圆弧分别交于C,D两点;③连接,并延长分别交于点E,F;④顺次连接,,,,,,得到六边形.连接,,交于点G,则下列结论错误的是( )
A.的内心与外心都是点G B.
C.点G是线段的三等分点 D.
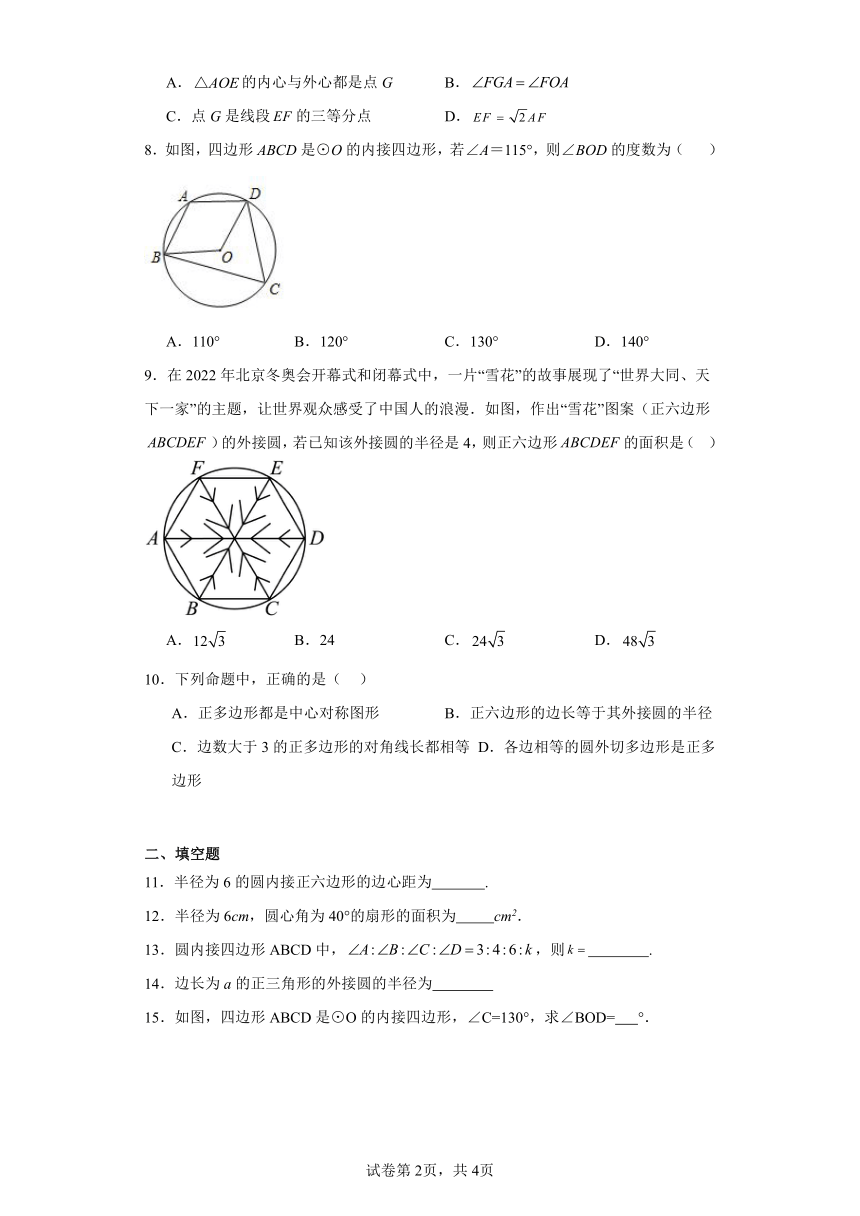
8.如图,四边形ABCD是⊙O的内接四边形,若∠A=115°,则∠BOD的度数为( )
A.110° B.120° C.130° D.140°
9.在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,若已知该外接圆的半径是4,则正六边形的面积是( )
A. B.24 C. D.
10.下列命题中,正确的是( )
A.正多边形都是中心对称图形 B.正六边形的边长等于其外接圆的半径
C.边数大于3的正多边形的对角线长都相等 D.各边相等的圆外切多边形是正多边形
二、填空题
11.半径为6的圆内接正六边形的边心距为 .
12.半径为6cm,圆心角为40°的扇形的面积为 cm2.
13.圆内接四边形ABCD中,,则 .
14.边长为a的正三角形的外接圆的半径为
15.如图,四边形ABCD是⊙O的内接四边形,∠C=130°,求∠BOD= °.
16.剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角后能够与它本身重合,则角可以为 度.(写出一个即可)
17.正方形的中心角为 .
18.若圆内接正方形的边心距为8,则这个圆的半径为 .
19.圆内接正方形的每条边所对的圆心角的度数是 .
20.四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是 ;△ODA的周长是 ;∠BOC的度数是 .
三、解答题
21.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=16°,= .求四边形ABCD各内角的度数.
22.如图,的半径为R,正方形,正方形分别是的内接正方形和外切正方形.求二者的边长比和面积比.
23.问题提出
(1)如图1,在中,,则的外接圆半径的值为______;
问题探究
(2)如图2,点P为正方形内一点,且,若,求的最小值.
问题解决.
(3)如图3,正方形是一个边长为的隔离区域设计图,为大门,点E在边上,.点P是正方形内设立的一个活动岗哨,到B、E的张角为,即,点A、D为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点Q,使得Q到A、D、P三个岗哨的距离和最小,试求的最小值.(保留根号或结果精确到,参考数据:)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.D
6.B
7.D
8.C
9.C
10.B
11..
12.4π
13.5
14.
15.100°
16.60
17.90°/90度
18.8
19./90度
20. r 3r 60°/60度
21.四边形ABCD各内角的度数为53°,74°,127°,106°.
22.,
23.(1)5;(2)2-2;(3)9
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若一个圆内接正多边形的内角是,则这个多边形是( )
A.正五边形 B.正六边形 C.正八边形 D.正十边形
2.下列命题错误的是( )
A.圆是轴对称图形 B.各边相等的圆内接多边形是正多边形
C.三角形的内心到它三边的距离相等 D.各角相等的圆内接多边形是正多边形
3.一个圆的内接正多边形中,一条边所对的圆心角为,则该正多边形的边数是( )
A.3 B.4 C.5 D.6
4.如果一个正多边形的中心角为,那么这个正多边形的边数是( ).
A. B. C. D.
5.下列命题是假命题的是( )
A.正五边形的内角和为540°
B.矩形的对角线相等
C.圆内接四边形的对角互补
D.对角线互相垂直的四边形是菱形
6.如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=130°,则∠BOD等于( )
A.90° B.100° C.120° D.130°
7.用尺规作某种六边形的方法,其步骤是:如图,①在上任取一点A,连接并延长交于点B;②以点B为圆心,为半径作圆弧分别交于C,D两点;③连接,并延长分别交于点E,F;④顺次连接,,,,,,得到六边形.连接,,交于点G,则下列结论错误的是( )
A.的内心与外心都是点G B.
C.点G是线段的三等分点 D.
8.如图,四边形ABCD是⊙O的内接四边形,若∠A=115°,则∠BOD的度数为( )
A.110° B.120° C.130° D.140°
9.在2022年北京冬奥会开幕式和闭幕式中,一片“雪花”的故事展现了“世界大同、天下一家”的主题,让世界观众感受了中国人的浪漫.如图,作出“雪花”图案(正六边形)的外接圆,若已知该外接圆的半径是4,则正六边形的面积是( )
A. B.24 C. D.
10.下列命题中,正确的是( )
A.正多边形都是中心对称图形 B.正六边形的边长等于其外接圆的半径
C.边数大于3的正多边形的对角线长都相等 D.各边相等的圆外切多边形是正多边形
二、填空题
11.半径为6的圆内接正六边形的边心距为 .
12.半径为6cm,圆心角为40°的扇形的面积为 cm2.
13.圆内接四边形ABCD中,,则 .
14.边长为a的正三角形的外接圆的半径为
15.如图,四边形ABCD是⊙O的内接四边形,∠C=130°,求∠BOD= °.
16.剪纸是中国最古老的民间艺术之一.如图,这个剪纸图案绕着它的中心旋转角后能够与它本身重合,则角可以为 度.(写出一个即可)
17.正方形的中心角为 .
18.若圆内接正方形的边心距为8,则这个圆的半径为 .
19.圆内接正方形的每条边所对的圆心角的度数是 .
20.四边形ABCD为⊙O的内接梯形,如图3所示,AB∥CD,且CD为直径,如果⊙O的半径等于r,∠C=60°,那图中△OAB的边长AB是 ;△ODA的周长是 ;∠BOC的度数是 .
三、解答题
21.如图,AB是半圆的直径,C、D是半圆上的两点,且∠BAC=16°,= .求四边形ABCD各内角的度数.
22.如图,的半径为R,正方形,正方形分别是的内接正方形和外切正方形.求二者的边长比和面积比.
23.问题提出
(1)如图1,在中,,则的外接圆半径的值为______;
问题探究
(2)如图2,点P为正方形内一点,且,若,求的最小值.
问题解决.
(3)如图3,正方形是一个边长为的隔离区域设计图,为大门,点E在边上,.点P是正方形内设立的一个活动岗哨,到B、E的张角为,即,点A、D为另两个固定岗哨.现需在隔离区域内部设置一个补水供给点Q,使得Q到A、D、P三个岗哨的距离和最小,试求的最小值.(保留根号或结果精确到,参考数据:)
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
2.D
3.C
4.B
5.D
6.B
7.D
8.C
9.C
10.B
11..
12.4π
13.5
14.
15.100°
16.60
17.90°/90度
18.8
19./90度
20. r 3r 60°/60度
21.四边形ABCD各内角的度数为53°,74°,127°,106°.
22.,
23.(1)5;(2)2-2;(3)9
答案第1页,共2页
答案第1页,共2页
同课章节目录
