专题19.4函数的图象 知识讲解(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题19.4函数的图象 知识讲解(含解析)2023-2024学年八年级数学下册人教版专项讲练 |
|
|
| 格式 | docx | ||
| 文件大小 | 513.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 19:51:39 | ||
图片预览

文档简介
专题 19.4 函数的图象(知识讲解)
【学习目标】
【要点梳理】
要点一、函数图象的定义
要点二、用描点法画函数的图象的一般步骤
列表;描点连线。
要点三、函数有三种表示形式:
【典型例题】
【类型一】图象的识别 从图象中读取信息
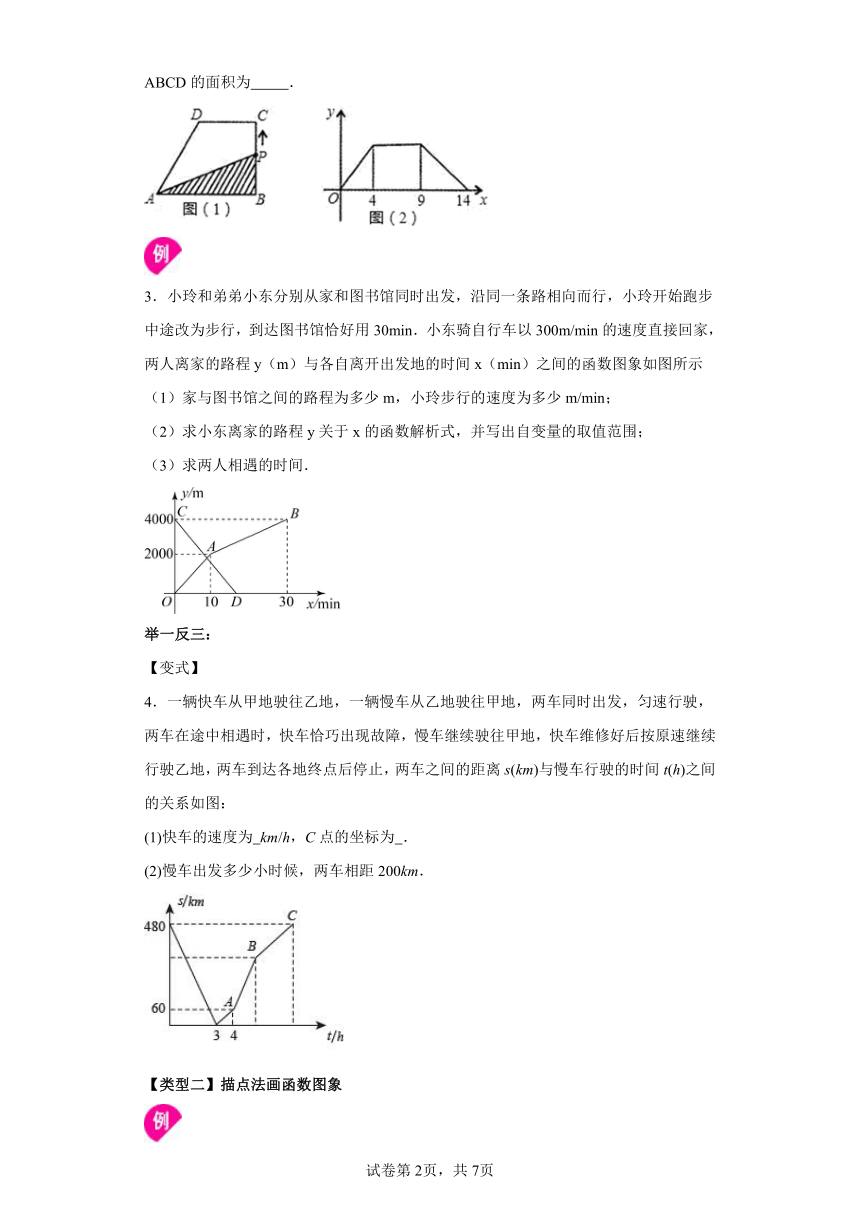
1.已知某函数图象如图所示,请回答下列问题:
(1)自变量x的取值范围是
(2)函数值y的取值范围是 ;
(3)当x=0时,y的对应值是 ;
(4)当x为 时,函数值最大;
(5)当y随x增大而增大时,x的取值范围是 ;
(6)当y随x的增大而减少时,x的取值范围是 .
举一反三:
【变式】
2.如图①,直角梯形ABCD中,动点P从B点出发,由B﹣C﹣D﹣A沿梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则直角梯形ABCD的面积为 .
3.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.
举一反三:
【变式】
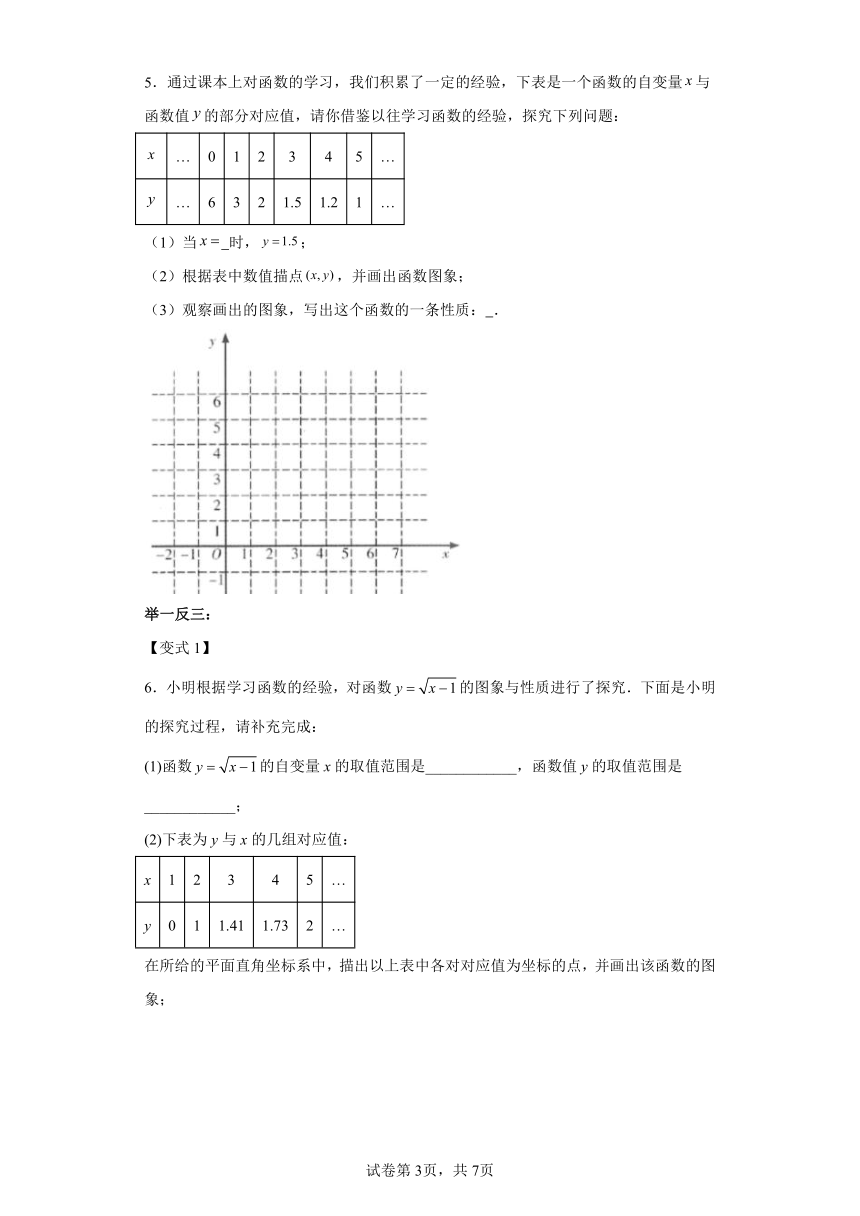
4.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)之间的关系如图:
(1)快车的速度为 km/h,C点的坐标为 .
(2)慢车出发多少小时候,两车相距200km.
【类型二】描点法画函数图象
5.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量与函数值的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
… 0 1 2 3 4 5 …
… 6 3 2 1.5 1.2 1 …
(1)当 时,;
(2)根据表中数值描点,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .
举一反三:
【变式1】
6.小明根据学习函数的经验,对函数的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
(1)函数的自变量x的取值范围是____________,函数值y的取值范围是____________;
(2)下表为y与x的几组对应值:
x 1 2 3 4 5 …
y 0 1 1.41 1.73 2 …
在所给的平面直角坐标系中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(3)当x=7时,对应的函数值y约为__________(精确到0.01);
(4)结合图象写出该函数的一条性质:____________________.
【变式2】
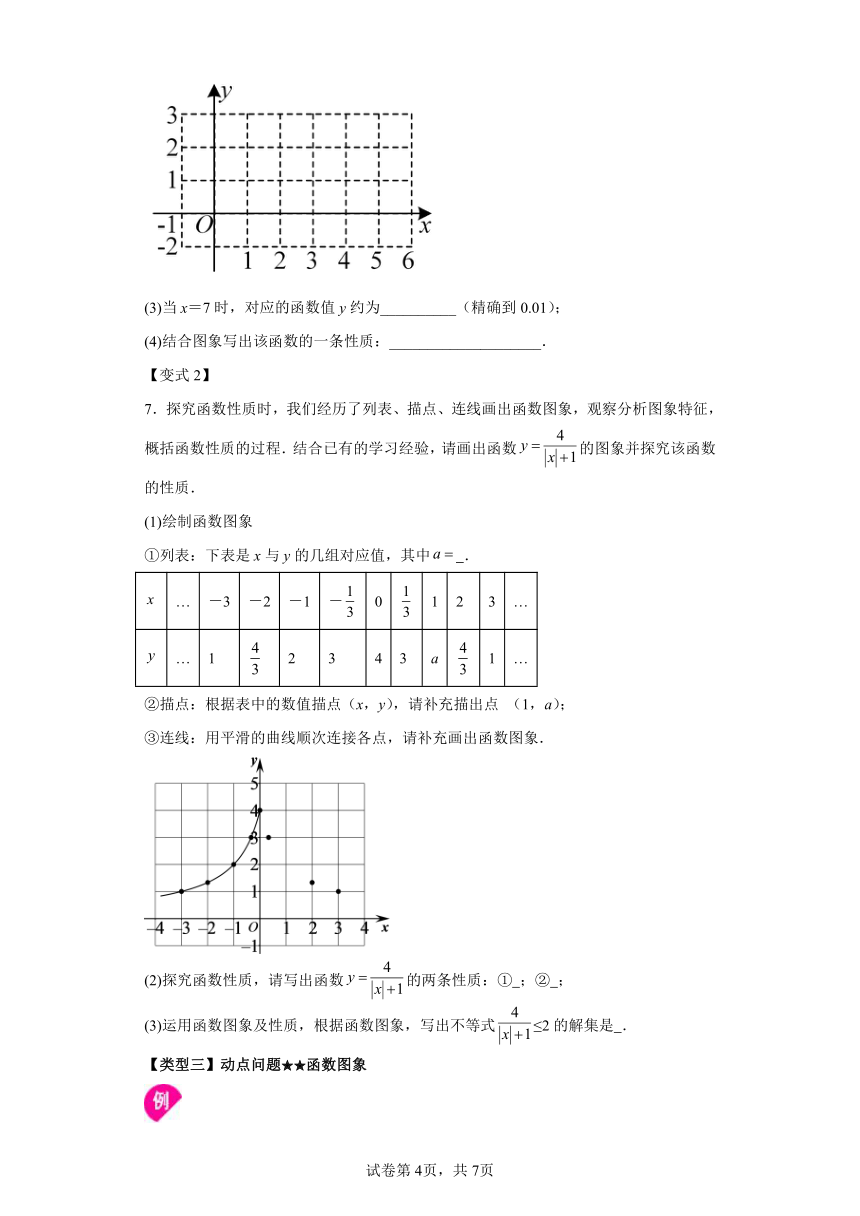
7.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.
(1)绘制函数图象
①列表:下表是x与y的几组对应值,其中 .
… -3 -2 -1 - 0 1 2 3 …
… 1 2 3 4 3 a 1 …
②描点:根据表中的数值描点(x,y),请补充描出点 (1,a);
③连线:用平滑的曲线顺次连接各点,请补充画出函数图象.
(2)探究函数性质,请写出函数的两条性质:① ;② ;
(3)运用函数图象及性质,根据函数图象,写出不等式≤2的解集是 .
【类型三】动点问题 函数图象
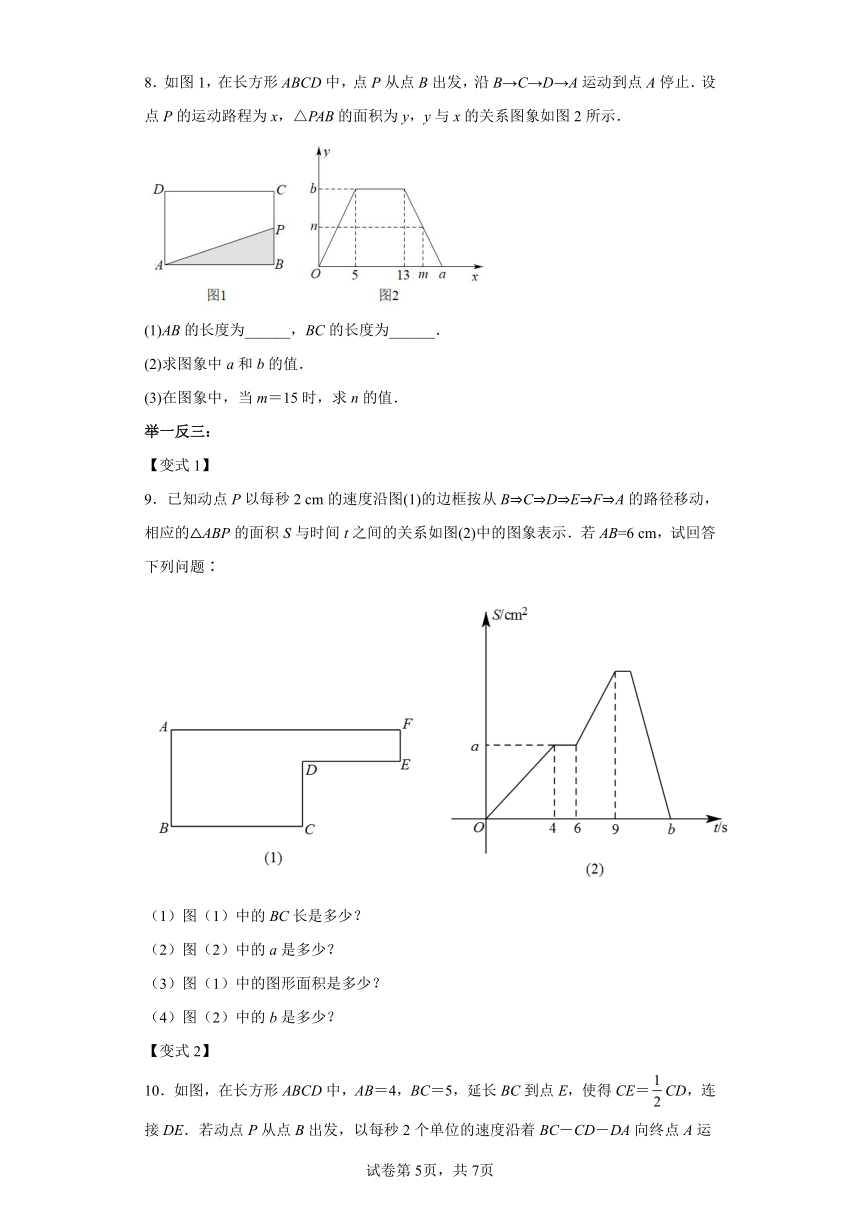
8.如图1,在长方形ABCD中,点P从点B出发,沿B→C→D→A运动到点A停止.设点P的运动路程为x,△PAB的面积为y,y与x的关系图象如图2所示.
(1)AB的长度为______,BC的长度为______.
(2)求图象中a和b的值.
(3)在图象中,当m=15时,求n的值.
举一反三:
【变式1】
9.已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题∶
(1)图(1)中的BC长是多少?
(2)图(2)中的a是多少?
(3)图(1)中的图形面积是多少?
(4)图(2)中的b是多少?
【变式2】
10.如图,在长方形ABCD中,AB=4,BC=5,延长BC到点E,使得CE=CD,连接DE.若动点P从点B出发,以每秒2个单位的速度沿着BC-CD-DA向终点A运动,设点P的运动时间为秒.
(1)在整个运动过程中,点P运动了多少时间?
(2)当为何值时,△ABP和△DCE全等;
(3)在整个运动过程中,求△ABP的面积.
【类型四】函数三种表达方式再训练
11.已知三角形的三边长分别为10cm,7cm,xcm,它的周长为ycm.
(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当x=6cm时,求三角形的周长;
(3)当x=18cm时,能求出三角形的周长吗?为什么?
举一反三:
【变式1】
12.如图,某品牌自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形,填写下表:
链条节数/x(节) 2 3 4 …
链条长度/y(cm) 4.2 …
(2)上表的两个变量中,自变量是 ;因变量是 ;
(3)请你写出y与x之间的关系式;
(4)如果一辆自行车的链条(安装前)共由60节链条组成,那么链条的总长度是多少?
【变式2】
13.某超市为方便顾客购买,将瓜子放入包装袋内出售,其质量x(kg)与售价y(元)之间的关系如下表(售价中的0.10元是包装袋的费用):
质量x/kg 售价y/元
1 15.00+0.10
2 30.00+0.10
3 45.00+0.10
4 60.00+0.10
…… ……
(1)观察表格,写出y与x之间的关系式.
(2)买8kg这种瓜子需花费多少元?
(3)用100元去买这种瓜子,最多能买多少千克?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)﹣4≤x≤3;(2)﹣2≤y≤4;(3)3;(4)1;(5)﹣2≤x≤1(6)﹣4≤x≤﹣2和1≤x≤3.
【分析】根据自变量的定义,函数值的定义以及二次函数的最值和增减性,观察函数图象分别写出即可.
【详解】解:(1)自变量x的取值范围是﹣4≤x≤3;
(2)函数y的取值范围是﹣2≤y≤4;
(3)当x=0时,y的对应值是3;
(4)当x为1时,函数值最大;
(5)当y随x的增大而增大时,x的取值范围是﹣2≤x≤1.
(6)当y随x的增大而减少时,x的取值范围是﹣4≤x≤﹣2和1≤x≤3;
故答案为(1)﹣4≤x≤3;(2)﹣2≤y≤4;(3)3;(4)1;(5)﹣2≤x≤1(6)﹣4≤x≤﹣2和1≤x≤3.
【点睛】本题考查二次函数的性质,函数图象,熟练掌握函数自变量的定义,函数值的定义以及函数的增减性并准确识图是解题关键.
2.26.
【分析】本题考查动点函数图象的问题,要根据图象判断出各边的边长.
【详解】动点P从B点出发,由B﹣C﹣D﹣A沿梯形的边运动;当运动到线段CD上时,三角形的面积的值开始固定.由图象可以看出,x为4时,面积开始不变,所以BC为4;
x为9时,面积不变结束,所以CD=9﹣4=5;
那么AD=14﹣9=5,AB=CD+
∴直角梯形ABCD的面积为×(5+8)×4=26.
【点睛】应根据题中所给的条件先判断出面积不变的开始与结束的点,进而判断出相应的线段的长度,再求解.
3.(1)家与图书馆之间路程为4000m,小玲步行速度为100m/s;(2)自变量x的范围为0≤x≤;(3)两人相遇时间为第8分钟.
【分析】(1)认真分析图象得到路程与速度数据;
(2)采用方程思想列出小东离家路程y与时间x之间的函数关系式;
(3)两人相遇实际上是函数图象求交点.
【详解】解:(1)结合题意和图象可知,线段CD为小东路程与时间函数图象,折现O﹣A﹣B为小玲路程与时间图象
则家与图书馆之间路程为4000m,小玲步行速度为(4000-2000)÷(30-10)=100m/s
(2)∵小东从离家4000m处以300m/min的速度返回家,则xmin时,
∴他离家的路程y=4000﹣300x,
自变量x的范围为0≤x≤,
(3)由图象可知,两人相遇是在小玲改变速度之前,
∴4000﹣300x=200x
解得x=8
∴两人相遇时间为第8分钟.
故答案为(1)4000,100;(2)y=4000﹣300x,0≤x≤;(3)第8分钟.
【点睛】本题考查了一次函数的应用,解决本题的关键是能从函数的图象中获取相关信息.
4.(1)100,(8,480);(2)1.75h和4.875h.
【分析】(1)由图像可知,甲乙两地的距离为480km, 0-3小时快车和慢车一起行驶了3小时,3-4小时快车出现故障停止前行、仅有慢车行驶,进而求出慢车速度,然后再求出快车的速度;A、B段为快车已维修好,两车共同行驶且快车在B点到站,BC段仅为慢车行驶;则可求出B点坐标,进而求出C点的横坐标即可解答;
(2)分快车出现故障前和故障后两种情况解答即可.
【详解】解:(1)由图像可知,甲乙两地的距离为480km
在0-3小时快车和慢车一起行驶了3小时,3-4小时快车出现故障停止前行、仅有慢车行驶
则慢车速度为=60km/h
设快车速度为v,则有:(v+60)×3=480,解得v=100km/h
∴B点的横坐标为+1=5.8,从坐标为60+(60+100)×(5.8-4)=348,即B(5.8,348)
∴慢车行驶时间为h,
∴C点的横坐标为8
∴C点的坐标为(8,480);
(2)在快车出现故障前,两车相距200km 所用时间为:(480-200)÷(100+60)=1.75h;
在快车出现故障后,慢车1小时行驶了60km,然后两车共同行驶了200-60=140km
共同行驶时间为140÷(100+60)=0.875h
∴两车相距200km 所用时间为4+0.875=4.875h.
答:两车相距200km 所用时间为1.75h和4.875h.
【点睛】本题考查了从函数图象中获取信息和行程问题,从函数图象中获取有用的信息成为解答本题的关键.
5.(1)3;(2)见解析;(3)函数图像与轴无限接近,但没有交点.
【分析】(1)观察列表即可得出答案;
(2)依照表格中的数据描出各个点,然后利用光滑的曲线连接各点即可;
(3)观察函数图像,写出一条符合函数图像的性质即可.
【详解】解:(1)通过观察表格发现:当时,,
故答案为:3;
(2)如下图:
(3)观察第(2)问中的图像可以得出一个结论:函数图像与轴无限接近,但没有交点;
【点睛】本题考查的是函数图象,主要让学生通过描点画出函数图象,从图象中读取相关的信息.
6.(1)x≥1,y≥0
(2)见解析
(3)2.45
(4)y随x的增大而增大(答案不唯一)
【分析】(1)根据二次根式的性质即可得出结论;
(2)在坐标系内描出各点,再顺次连接即可;
(3)把x=7代入函数解析式,求出y的值即可;
(4)根据函数图象即可得出结论.
【详解】(1)解:函数的自变量x的取值范围是x≥1,函数函数值y的取值范围是y≥0;
故答案为:x≥1,y≥0;
(2)解:如图所示:
(3)解:当x=7时,对应的函数值=≈2.45,
故答案为:2.45;
(4)解:由图象可知,y随x的增大而增大.
故答案为:y随x的增大而增大(答案不唯一).
【点睛】本题考查了函数的图象,根据题意画出函数图象,利用数形结合求解是解答此题的关键.
7.(1)①2;②见解析;③见解析
(2)①函数图象关于y轴对称;②当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
(3)x≤-1或x≥1
【分析】(1)①将x=1代入即可求a;②描出点(1,a);③请画出函数图象.
(2)写出两条符合图象的性质即可;
(3)根据图象即可求得.
【详解】(1)解:①当x=1,=,②(点如下图所示),③(图象如下图所示);
(2)由图象可知,①函数图像关于y轴对称;②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)由图象可知,当x=±1,y=2;x≤-1或x≥1时,y≤2,
∴不等式≤2的解集是x≤-1或x≥1.
【点睛】本题考查了函数的图形及性质,解题的关键是熟练掌握研究函数的方法:用列表、描点、连线作出图象,再数形结合研究函数性质.
8.(1)8、5
(2)a=18、b=20
(3)12
【分析】(1)根据函数图象直接可得答案;
(2)利用三角形的面积公式结合图象可得a和b的值;
(3)首先确定点P在AD上,求出AP的长,再代入三角形面积公式即可.
【详解】(1)解:由图2知,当x=5时,点P与C重合,
∴BC=5,
当x=13时,点P与D重合,
∴BC+CD=13,
∴CD=8=AB,
故答案为:8,5;
(2)当P与C点重合时,
=,
当点P与A重合时,
=5+8+5=18;
(3)∵,
∴此时点P在AD边上,且AP=3.
∴.
【点睛】题目主要考查函数图象中的动点问题,理解题意,结合函数图象及图形得出相关信息是解题关键.
9.(1)8cm;(2)24cm2;(3)60cm2;(4)17
【分析】(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案;
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
【详解】(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(cm) ;
(2)a=S△ABC=×6×8=24(cm 2) ;
(3)同理,由图象知 CD=4cm,DE=6cm,则EF=2cm,AF=14 cm
∴图(1)中的图象面积为6×14-4×6=60cm 2 ;
(4)图(1)中的多边形的周长为(14+6)×2=40cm b=(40-6)÷2=17秒.
10.(1)7秒
(2)当或时,△ABP和△DCP全等
(3)
【分析】(1)利用时间=总路程÷速度计算即可;
(2)先求出CE=2,当P在BC上时,若△ABP与△DCE全等,则,;当P在AD上时,若△ABP与△DCE全等,则,,然后根据时间路程的关系可求t的值;
(3)分P在BC,CD,AD上进行讨论即可.
【详解】(1)解:∵长方形ABCD中,AB=4,BC=5,
∴AD=BC=5,CD=AB=4,
∴在整个运动过程中,点P运动的时间t=(5+4+5)÷2=7(秒);
(2)解:由题意,知AB=CD=4,AD=BC=5, CE=CD=2,
①当P在BC上时,
∵△ABP与△DCE全等,,
∴,
∴,
∴;
②当P在AD上时,
∵△ABP与△DCE全等,,
∴,,
∴,
∴,
综上,当或时,△ABP和△DCP全等;
(3)解:当P在BC上,即时,
;
当P在CD上,即时,
;
当P在AD上,即时,
;
综上,.
【点睛】本题考查了全等三角形的性质,三角形的面积公式等知识,运用分类思想是解题的关键.
11.(1)3<x<17;(2)23cm;(3)不能求三角形的周长,理由见解析.
【分析】(1)根据三角形周长公式得出y与x的函数关系式即可,再利用三角形三边关系得出x的取值范围;
(2)将x=6代入求出周长;
(3)利用(1)中所求x的取值范围得出答案.
【详解】(1)由题意可得出:y=10+7+x=17+x.
∵10﹣7<x<10+7,
∴3<x<17.
(2)当x=6时,y=17+6=23cm;
(3)∵x=18不在范围3<x<17内,
∴不能求三角形的周长.
【点睛】此题主要考查了三角形三边关系以及函数值求法等知识,根据三角形的三边关系得出是解题关键.
12.(1)5.9,7.6;(2)链条节数;链条长度;(3)y=1.7x+0.8;(4)这辆自行车链条的总长为102cm.
【分析】(1)根据图形找规律,即可求得;
(2)根据函数的知识,链条的长度随着链条的节数变化而变化,即可求得;
(3)根据(1)的结论写出解析式即可;
(4)根据(3)解析式代入求解,最后根据实际情况,减去一个交叉重叠部分的圆的直径.
【详解】(1)根据图形可得:
2节链条的长度为2.5×2﹣0.8=4.2(cm),
3节链条的长度为2.5×3﹣0.8×2=5.9(cm),
4节链条的长度为2.5×4﹣0.8×3=7.6(cm),
故答案为:5.9,7.6;
(2)链条的长度随着链条的节数变化而变化
自变量是链条节数,因变量是链条长度;
故答案为:链条节数;链条长度;
(3)由(1)可得x节链条长为:
y=2.5x﹣0.8(x﹣1)=1.7x+0.8,
∴y与x之间的关系式为y=1.7x+0.8;
(4)∵自行车上的链条为环形,在展直的基础上还要减少0.8cm,
∴这辆自行车链条的总长为1.7×60+0.8﹣0.8=102(cm).
【点睛】本题考查了函数的表示方法,求函数的解析式,函数的定义,掌握函数的相关知识是解题的关键.
13.(1)y=15x+0.1;(2)120.1元;(3)6.66 kg
【分析】(1)由表格中的数据可知:每kg瓜子的价格为:15元,由此即可得到y与x之间的关系式;
(2)将代入(1)中所得关系式即可得到对应的的值;
(3)将代入(1)中所得关系式,求得对应的的值即可;
【详解】解:(1)观察、分析表格中的数据可得:
当时,,
当时,,
当时,,
当时,,
…
∴售价(元)与数量(千克)之间的数量关系的表达式为;
(2)当时,(元);
(3)当时,由(1)可得:,解得:,
∴用100元去买这种瓜子,最多能买6.66kg.
【点睛】本题考查了列代数式,代数式求值,读懂图表信息是解题的关键,另外,分析解答本题时,不要忽略了条件“买瓜子需支付0.1元的包装袋费用”,且“包装袋费用与购买瓜子的数量无关”.
答案第1页,共2页
答案第1页,共2页
【学习目标】
【要点梳理】
要点一、函数图象的定义
要点二、用描点法画函数的图象的一般步骤
列表;描点连线。
要点三、函数有三种表示形式:
【典型例题】
【类型一】图象的识别 从图象中读取信息
1.已知某函数图象如图所示,请回答下列问题:
(1)自变量x的取值范围是
(2)函数值y的取值范围是 ;
(3)当x=0时,y的对应值是 ;
(4)当x为 时,函数值最大;
(5)当y随x增大而增大时,x的取值范围是 ;
(6)当y随x的增大而减少时,x的取值范围是 .
举一反三:
【变式】
2.如图①,直角梯形ABCD中,动点P从B点出发,由B﹣C﹣D﹣A沿梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则直角梯形ABCD的面积为 .
3.小玲和弟弟小东分别从家和图书馆同时出发,沿同一条路相向而行,小玲开始跑步中途改为步行,到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家,两人离家的路程y(m)与各自离开出发地的时间x(min)之间的函数图象如图所示
(1)家与图书馆之间的路程为多少m,小玲步行的速度为多少m/min;
(2)求小东离家的路程y关于x的函数解析式,并写出自变量的取值范围;
(3)求两人相遇的时间.
举一反三:
【变式】
4.一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶,两车在途中相遇时,快车恰巧出现故障,慢车继续驶往甲地,快车维修好后按原速继续行驶乙地,两车到达各地终点后停止,两车之间的距离s(km)与慢车行驶的时间t(h)之间的关系如图:
(1)快车的速度为 km/h,C点的坐标为 .
(2)慢车出发多少小时候,两车相距200km.
【类型二】描点法画函数图象
5.通过课本上对函数的学习,我们积累了一定的经验,下表是一个函数的自变量与函数值的部分对应值,请你借鉴以往学习函数的经验,探究下列问题:
… 0 1 2 3 4 5 …
… 6 3 2 1.5 1.2 1 …
(1)当 时,;
(2)根据表中数值描点,并画出函数图象;
(3)观察画出的图象,写出这个函数的一条性质: .
举一反三:
【变式1】
6.小明根据学习函数的经验,对函数的图象与性质进行了探究.下面是小明的探究过程,请补充完成:
(1)函数的自变量x的取值范围是____________,函数值y的取值范围是____________;
(2)下表为y与x的几组对应值:
x 1 2 3 4 5 …
y 0 1 1.41 1.73 2 …
在所给的平面直角坐标系中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(3)当x=7时,对应的函数值y约为__________(精确到0.01);
(4)结合图象写出该函数的一条性质:____________________.
【变式2】
7.探究函数性质时,我们经历了列表、描点、连线画出函数图象,观察分析图象特征,概括函数性质的过程.结合已有的学习经验,请画出函数的图象并探究该函数的性质.
(1)绘制函数图象
①列表:下表是x与y的几组对应值,其中 .
… -3 -2 -1 - 0 1 2 3 …
… 1 2 3 4 3 a 1 …
②描点:根据表中的数值描点(x,y),请补充描出点 (1,a);
③连线:用平滑的曲线顺次连接各点,请补充画出函数图象.
(2)探究函数性质,请写出函数的两条性质:① ;② ;
(3)运用函数图象及性质,根据函数图象,写出不等式≤2的解集是 .
【类型三】动点问题 函数图象
8.如图1,在长方形ABCD中,点P从点B出发,沿B→C→D→A运动到点A停止.设点P的运动路程为x,△PAB的面积为y,y与x的关系图象如图2所示.
(1)AB的长度为______,BC的长度为______.
(2)求图象中a和b的值.
(3)在图象中,当m=15时,求n的值.
举一反三:
【变式1】
9.已知动点P以每秒2 cm的速度沿图(1)的边框按从B C D E F A的路径移动,相应的△ABP的面积S与时间t之间的关系如图(2)中的图象表示.若AB=6 cm,试回答下列问题∶
(1)图(1)中的BC长是多少?
(2)图(2)中的a是多少?
(3)图(1)中的图形面积是多少?
(4)图(2)中的b是多少?
【变式2】
10.如图,在长方形ABCD中,AB=4,BC=5,延长BC到点E,使得CE=CD,连接DE.若动点P从点B出发,以每秒2个单位的速度沿着BC-CD-DA向终点A运动,设点P的运动时间为秒.
(1)在整个运动过程中,点P运动了多少时间?
(2)当为何值时,△ABP和△DCE全等;
(3)在整个运动过程中,求△ABP的面积.
【类型四】函数三种表达方式再训练
11.已知三角形的三边长分别为10cm,7cm,xcm,它的周长为ycm.
(1)求y关于x的函数解析式和自变量x的取值范围;
(2)当x=6cm时,求三角形的周长;
(3)当x=18cm时,能求出三角形的周长吗?为什么?
举一反三:
【变式1】
12.如图,某品牌自行车每节链条的长度为2.5cm,交叉重叠部分的圆的直径为0.8cm.
(1)观察图形,填写下表:
链条节数/x(节) 2 3 4 …
链条长度/y(cm) 4.2 …
(2)上表的两个变量中,自变量是 ;因变量是 ;
(3)请你写出y与x之间的关系式;
(4)如果一辆自行车的链条(安装前)共由60节链条组成,那么链条的总长度是多少?
【变式2】
13.某超市为方便顾客购买,将瓜子放入包装袋内出售,其质量x(kg)与售价y(元)之间的关系如下表(售价中的0.10元是包装袋的费用):
质量x/kg 售价y/元
1 15.00+0.10
2 30.00+0.10
3 45.00+0.10
4 60.00+0.10
…… ……
(1)观察表格,写出y与x之间的关系式.
(2)买8kg这种瓜子需花费多少元?
(3)用100元去买这种瓜子,最多能买多少千克?
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.(1)﹣4≤x≤3;(2)﹣2≤y≤4;(3)3;(4)1;(5)﹣2≤x≤1(6)﹣4≤x≤﹣2和1≤x≤3.
【分析】根据自变量的定义,函数值的定义以及二次函数的最值和增减性,观察函数图象分别写出即可.
【详解】解:(1)自变量x的取值范围是﹣4≤x≤3;
(2)函数y的取值范围是﹣2≤y≤4;
(3)当x=0时,y的对应值是3;
(4)当x为1时,函数值最大;
(5)当y随x的增大而增大时,x的取值范围是﹣2≤x≤1.
(6)当y随x的增大而减少时,x的取值范围是﹣4≤x≤﹣2和1≤x≤3;
故答案为(1)﹣4≤x≤3;(2)﹣2≤y≤4;(3)3;(4)1;(5)﹣2≤x≤1(6)﹣4≤x≤﹣2和1≤x≤3.
【点睛】本题考查二次函数的性质,函数图象,熟练掌握函数自变量的定义,函数值的定义以及函数的增减性并准确识图是解题关键.
2.26.
【分析】本题考查动点函数图象的问题,要根据图象判断出各边的边长.
【详解】动点P从B点出发,由B﹣C﹣D﹣A沿梯形的边运动;当运动到线段CD上时,三角形的面积的值开始固定.由图象可以看出,x为4时,面积开始不变,所以BC为4;
x为9时,面积不变结束,所以CD=9﹣4=5;
那么AD=14﹣9=5,AB=CD+
∴直角梯形ABCD的面积为×(5+8)×4=26.
【点睛】应根据题中所给的条件先判断出面积不变的开始与结束的点,进而判断出相应的线段的长度,再求解.
3.(1)家与图书馆之间路程为4000m,小玲步行速度为100m/s;(2)自变量x的范围为0≤x≤;(3)两人相遇时间为第8分钟.
【分析】(1)认真分析图象得到路程与速度数据;
(2)采用方程思想列出小东离家路程y与时间x之间的函数关系式;
(3)两人相遇实际上是函数图象求交点.
【详解】解:(1)结合题意和图象可知,线段CD为小东路程与时间函数图象,折现O﹣A﹣B为小玲路程与时间图象
则家与图书馆之间路程为4000m,小玲步行速度为(4000-2000)÷(30-10)=100m/s
(2)∵小东从离家4000m处以300m/min的速度返回家,则xmin时,
∴他离家的路程y=4000﹣300x,
自变量x的范围为0≤x≤,
(3)由图象可知,两人相遇是在小玲改变速度之前,
∴4000﹣300x=200x
解得x=8
∴两人相遇时间为第8分钟.
故答案为(1)4000,100;(2)y=4000﹣300x,0≤x≤;(3)第8分钟.
【点睛】本题考查了一次函数的应用,解决本题的关键是能从函数的图象中获取相关信息.
4.(1)100,(8,480);(2)1.75h和4.875h.
【分析】(1)由图像可知,甲乙两地的距离为480km, 0-3小时快车和慢车一起行驶了3小时,3-4小时快车出现故障停止前行、仅有慢车行驶,进而求出慢车速度,然后再求出快车的速度;A、B段为快车已维修好,两车共同行驶且快车在B点到站,BC段仅为慢车行驶;则可求出B点坐标,进而求出C点的横坐标即可解答;
(2)分快车出现故障前和故障后两种情况解答即可.
【详解】解:(1)由图像可知,甲乙两地的距离为480km
在0-3小时快车和慢车一起行驶了3小时,3-4小时快车出现故障停止前行、仅有慢车行驶
则慢车速度为=60km/h
设快车速度为v,则有:(v+60)×3=480,解得v=100km/h
∴B点的横坐标为+1=5.8,从坐标为60+(60+100)×(5.8-4)=348,即B(5.8,348)
∴慢车行驶时间为h,
∴C点的横坐标为8
∴C点的坐标为(8,480);
(2)在快车出现故障前,两车相距200km 所用时间为:(480-200)÷(100+60)=1.75h;
在快车出现故障后,慢车1小时行驶了60km,然后两车共同行驶了200-60=140km
共同行驶时间为140÷(100+60)=0.875h
∴两车相距200km 所用时间为4+0.875=4.875h.
答:两车相距200km 所用时间为1.75h和4.875h.
【点睛】本题考查了从函数图象中获取信息和行程问题,从函数图象中获取有用的信息成为解答本题的关键.
5.(1)3;(2)见解析;(3)函数图像与轴无限接近,但没有交点.
【分析】(1)观察列表即可得出答案;
(2)依照表格中的数据描出各个点,然后利用光滑的曲线连接各点即可;
(3)观察函数图像,写出一条符合函数图像的性质即可.
【详解】解:(1)通过观察表格发现:当时,,
故答案为:3;
(2)如下图:
(3)观察第(2)问中的图像可以得出一个结论:函数图像与轴无限接近,但没有交点;
【点睛】本题考查的是函数图象,主要让学生通过描点画出函数图象,从图象中读取相关的信息.
6.(1)x≥1,y≥0
(2)见解析
(3)2.45
(4)y随x的增大而增大(答案不唯一)
【分析】(1)根据二次根式的性质即可得出结论;
(2)在坐标系内描出各点,再顺次连接即可;
(3)把x=7代入函数解析式,求出y的值即可;
(4)根据函数图象即可得出结论.
【详解】(1)解:函数的自变量x的取值范围是x≥1,函数函数值y的取值范围是y≥0;
故答案为:x≥1,y≥0;
(2)解:如图所示:
(3)解:当x=7时,对应的函数值=≈2.45,
故答案为:2.45;
(4)解:由图象可知,y随x的增大而增大.
故答案为:y随x的增大而增大(答案不唯一).
【点睛】本题考查了函数的图象,根据题意画出函数图象,利用数形结合求解是解答此题的关键.
7.(1)①2;②见解析;③见解析
(2)①函数图象关于y轴对称;②当x<0时,y随x的增大而增大;当x>0时,y随x的增大而减小
(3)x≤-1或x≥1
【分析】(1)①将x=1代入即可求a;②描出点(1,a);③请画出函数图象.
(2)写出两条符合图象的性质即可;
(3)根据图象即可求得.
【详解】(1)解:①当x=1,=,②(点如下图所示),③(图象如下图所示);
(2)由图象可知,①函数图像关于y轴对称;②当x<0时,y随x的增大而增大,当x>0时,y随x的增大而减小;
(3)由图象可知,当x=±1,y=2;x≤-1或x≥1时,y≤2,
∴不等式≤2的解集是x≤-1或x≥1.
【点睛】本题考查了函数的图形及性质,解题的关键是熟练掌握研究函数的方法:用列表、描点、连线作出图象,再数形结合研究函数性质.
8.(1)8、5
(2)a=18、b=20
(3)12
【分析】(1)根据函数图象直接可得答案;
(2)利用三角形的面积公式结合图象可得a和b的值;
(3)首先确定点P在AD上,求出AP的长,再代入三角形面积公式即可.
【详解】(1)解:由图2知,当x=5时,点P与C重合,
∴BC=5,
当x=13时,点P与D重合,
∴BC+CD=13,
∴CD=8=AB,
故答案为:8,5;
(2)当P与C点重合时,
=,
当点P与A重合时,
=5+8+5=18;
(3)∵,
∴此时点P在AD边上,且AP=3.
∴.
【点睛】题目主要考查函数图象中的动点问题,理解题意,结合函数图象及图形得出相关信息是解题关键.
9.(1)8cm;(2)24cm2;(3)60cm2;(4)17
【分析】(1)根据题意得:动点P在BC上运动的时间是4秒,又由动点的速度,可得BC的长;
(2)由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
(3)分析图形可得,甲中的图形面积等于AB×AF-CD×DE,根据图象求出CD和DE的长,代入数据计算可得答案;
(4)计算BC+CD+DE+EF+FA的长度,又由P的速度,计算可得b的值.
【详解】(1)由图象知,当t由0增大到4时,点P由B C,∴BC==4×2=8(cm) ;
(2)a=S△ABC=×6×8=24(cm 2) ;
(3)同理,由图象知 CD=4cm,DE=6cm,则EF=2cm,AF=14 cm
∴图(1)中的图象面积为6×14-4×6=60cm 2 ;
(4)图(1)中的多边形的周长为(14+6)×2=40cm b=(40-6)÷2=17秒.
10.(1)7秒
(2)当或时,△ABP和△DCP全等
(3)
【分析】(1)利用时间=总路程÷速度计算即可;
(2)先求出CE=2,当P在BC上时,若△ABP与△DCE全等,则,;当P在AD上时,若△ABP与△DCE全等,则,,然后根据时间路程的关系可求t的值;
(3)分P在BC,CD,AD上进行讨论即可.
【详解】(1)解:∵长方形ABCD中,AB=4,BC=5,
∴AD=BC=5,CD=AB=4,
∴在整个运动过程中,点P运动的时间t=(5+4+5)÷2=7(秒);
(2)解:由题意,知AB=CD=4,AD=BC=5, CE=CD=2,
①当P在BC上时,
∵△ABP与△DCE全等,,
∴,
∴,
∴;
②当P在AD上时,
∵△ABP与△DCE全等,,
∴,,
∴,
∴,
综上,当或时,△ABP和△DCP全等;
(3)解:当P在BC上,即时,
;
当P在CD上,即时,
;
当P在AD上,即时,
;
综上,.
【点睛】本题考查了全等三角形的性质,三角形的面积公式等知识,运用分类思想是解题的关键.
11.(1)3<x<17;(2)23cm;(3)不能求三角形的周长,理由见解析.
【分析】(1)根据三角形周长公式得出y与x的函数关系式即可,再利用三角形三边关系得出x的取值范围;
(2)将x=6代入求出周长;
(3)利用(1)中所求x的取值范围得出答案.
【详解】(1)由题意可得出:y=10+7+x=17+x.
∵10﹣7<x<10+7,
∴3<x<17.
(2)当x=6时,y=17+6=23cm;
(3)∵x=18不在范围3<x<17内,
∴不能求三角形的周长.
【点睛】此题主要考查了三角形三边关系以及函数值求法等知识,根据三角形的三边关系得出是解题关键.
12.(1)5.9,7.6;(2)链条节数;链条长度;(3)y=1.7x+0.8;(4)这辆自行车链条的总长为102cm.
【分析】(1)根据图形找规律,即可求得;
(2)根据函数的知识,链条的长度随着链条的节数变化而变化,即可求得;
(3)根据(1)的结论写出解析式即可;
(4)根据(3)解析式代入求解,最后根据实际情况,减去一个交叉重叠部分的圆的直径.
【详解】(1)根据图形可得:
2节链条的长度为2.5×2﹣0.8=4.2(cm),
3节链条的长度为2.5×3﹣0.8×2=5.9(cm),
4节链条的长度为2.5×4﹣0.8×3=7.6(cm),
故答案为:5.9,7.6;
(2)链条的长度随着链条的节数变化而变化
自变量是链条节数,因变量是链条长度;
故答案为:链条节数;链条长度;
(3)由(1)可得x节链条长为:
y=2.5x﹣0.8(x﹣1)=1.7x+0.8,
∴y与x之间的关系式为y=1.7x+0.8;
(4)∵自行车上的链条为环形,在展直的基础上还要减少0.8cm,
∴这辆自行车链条的总长为1.7×60+0.8﹣0.8=102(cm).
【点睛】本题考查了函数的表示方法,求函数的解析式,函数的定义,掌握函数的相关知识是解题的关键.
13.(1)y=15x+0.1;(2)120.1元;(3)6.66 kg
【分析】(1)由表格中的数据可知:每kg瓜子的价格为:15元,由此即可得到y与x之间的关系式;
(2)将代入(1)中所得关系式即可得到对应的的值;
(3)将代入(1)中所得关系式,求得对应的的值即可;
【详解】解:(1)观察、分析表格中的数据可得:
当时,,
当时,,
当时,,
当时,,
…
∴售价(元)与数量(千克)之间的数量关系的表达式为;
(2)当时,(元);
(3)当时,由(1)可得:,解得:,
∴用100元去买这种瓜子,最多能买6.66kg.
【点睛】本题考查了列代数式,代数式求值,读懂图表信息是解题的关键,另外,分析解答本题时,不要忽略了条件“买瓜子需支付0.1元的包装袋费用”,且“包装袋费用与购买瓜子的数量无关”.
答案第1页,共2页
答案第1页,共2页
