专题19.3变量与函数 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练
文档属性
| 名称 | 专题19.3变量与函数 巩固篇 专项练习(含解析)2023-2024学年八年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 846.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-28 19:59:16 | ||
图片预览


文档简介
专题 19.3 变量与函数(巩固篇)(专项练习)
一、单选题
1.下列图像不能表示是的函数的是( )
A.B. C.D.
2.下列关系式中,y不是x的函数的是( )
A. B. C. D.
3.已知,那么的值是( )
A.-6 B.-9 C.9 D.6
4.水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
5.等腰三角形的周长是,腰长是底边长的函数,此函数解析式和自变量取值范围正确的是( )
A. B.
C. D.
6.函数y=中,自变量x的取值范围在数轴上表示正确的是( )
A. B.C. D.
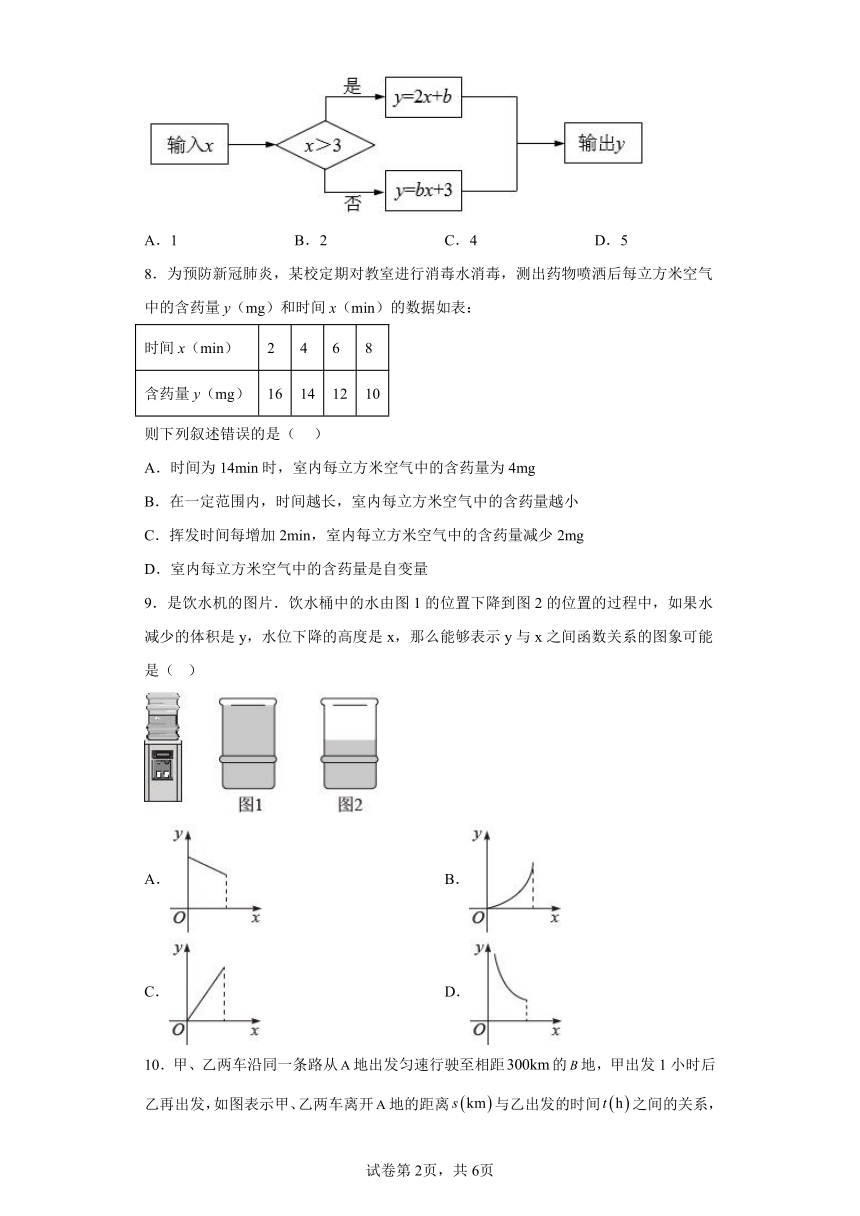
7.根据如图所示的程序计算函数y的值,若输入x的值为4时,输出的y的值为7,则输入x的值为2时,输出的y的值为( )
A.1 B.2 C.4 D.5
8.为预防新冠肺炎,某校定期对教室进行消毒水消毒,测出药物喷洒后每立方米空气中的含药量y(mg)和时间x(min)的数据如表:
时间x(min) 2 4 6 8
含药量y(mg) 16 14 12 10
则下列叙述错误的是( )
A.时间为14min时,室内每立方米空气中的含药量为4mg
B.在一定范围内,时间越长,室内每立方米空气中的含药量越小
C.挥发时间每增加2min,室内每立方米空气中的含药量减少2mg
D.室内每立方米空气中的含药量是自变量
9.是饮水机的图片.饮水桶中的水由图1的位置下降到图2的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A. B.
C. D.
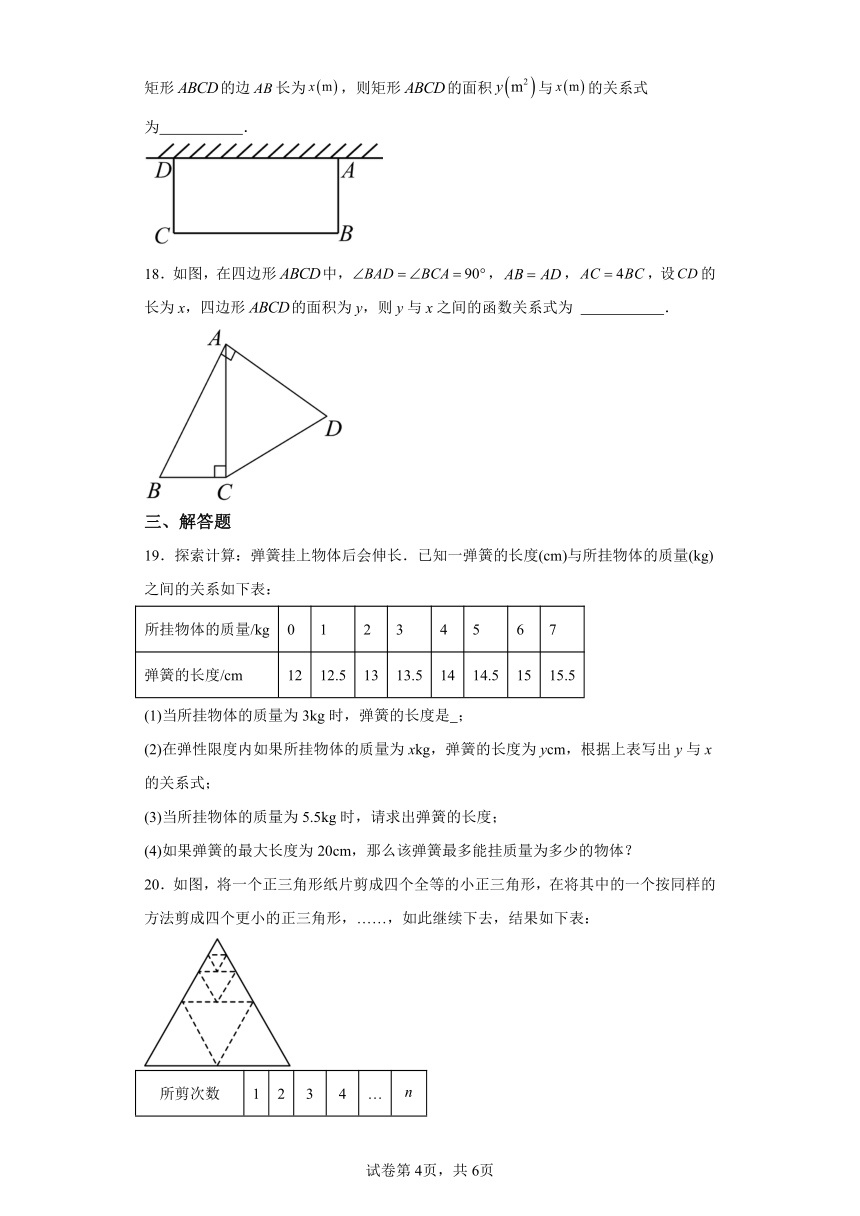
10.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
二、填空题
11.函数自变量x的取值范围是 .
12.下列变量间的关系是函数关系的有 (填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
13.若函数,则当函数值时,自变量的值为 .
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为 .
15.已知,且满足表示不超过的最大整数),则的值可以为 .
16.声音在空气中传播的速度y(米/秒)(简称音速)与气温之间的关系如下:
气温 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
从表中可知音速y随温度x的升高而 .在气温为的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点 米.
17.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形的边长为,则矩形的面积与的关系式为 .
18.如图,在四边形中,,,,设的长为x,四边形的面积为y,则y与x之间的函数关系式为 .
三、解答题
19.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3kg时,弹簧的长度是 ;
(2)在弹性限度内如果所挂物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20cm,那么该弹簧最多能挂质量为多少的物体?
20.如图,将一个正三角形纸片剪成四个全等的小正三角形,在将其中的一个按同样的方法剪成四个更小的正三角形,……,如此继续下去,结果如下表:
所剪次数 1 2 3 4 …
正三角形个数 4 7 10 13 …
(1)上表中自变量和因变量分别是___________.
(2)当所剪次数为4次时,正三角形的个数是___________
(3)求与的关系式:___________
(4)当所剪次数为10次时,求正三角形的个数___________.
21.开通了,中国联通公司公布了收费标准,其中包月129元时,超出部分国内拨打话元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 1 2 3 4 5 …
电话费/元 …
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示国内拨打超出时间,y表示国内拨打超出部分的电话费,那么y与x的关系式是什么?
(3)如果国内拨打电话超出10分钟,需多付多少电话费?
(4)某次超出部分国内拨打电话的费用是元,那么小明的爸爸国内拨打电话超出几分钟?
22.为了帮助经济相对薄弱村发展经济,将真正的实惠带给消费者,某市在各菜市场开设了“爱心助农销售专区”.现从某村购进苹果和橙子进行销售,进价分别为每箱40元和60元,该专区决定苹果以每箱60元出售,橙子以每箱88元出售.
(1)若购进苹果120箱,橙子200箱,可获利______元;
(2)为满足市场需求,需购进这两种水果共1000箱,设购进苹果m箱,获得的利润为W元.
①请求出获利W(元)与购进苹果箱数m(箱)之间的函数表达式;
②若此次活动该村获润不低于25000元,则最多销售多少箱苹果?
23.防疫期间,某药店销售一批外科口罩,如果一次性购买 40 个以上的外科口罩,超过 40 个部分按优惠价出售.上个月小王家一次性买了外科口罩 90 个,花了 65 元;小李家一次性买了外科口罩 120 个, 花了 80 元.
(1)求销售一个外科口罩的原价和优惠价分别是多少?
(2)设一次性购买外科口罩 x 个,花费 y 元,写出 y 与 x 之间的函数关系式.
(3)这个月学校一次性购买该外科口罩1080 个,花了多少钱?
24.如图,在等腰中,,,,动点P以的速度从点B出发,沿边向终点C运动,过P作于点Q,以为邻边作平行四边形.设点P的运动时间为t(s),与重叠部分图形面积为.
(1)当点M落在边上时,求t的值;
(2)求S与t的函数关系,并直接写出自变量t的取值范围.
试卷第4页,共6页
试卷第3页,共6页
参考答案:
1.B
【分析】根据函数的图象可知对于x的每一个值y都有唯一的值与之相对应进行判定即可.
【详解】根据函数的概念:如果在一个变化过程中,有两个变量x、y,对于x的每一个值,y都有唯一确定的值与之对应,这时称y是x的函数.
选项B,对于一个x有两个y与之对应,故不是函数图象,
故选:B.
【点睛】本题主要考查了函数的图象,以及函数的表示方法,解题的关键是函数的定义,属于基础题.
2.C
【分析】根据函数的概念可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此分析每一选项即可得出答案.
【详解】A. 符合函数定义,是函数,故选项错误,不符合题意;
B. 符合函数定义,是函数,故选项错误,不符合题意;
C. 对于x的每一个取值(),y都有两个值,不是函数,故选项正确,符合题意;
D. 符合函数定义,是函数,故选项错误,不符合题意.
故选:C
【点睛】本题考查了函数的定义,一般地,在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量.
3.C
【分析】由于和中的被开方数互为相反数,根据二次根式的性质可以得到,由此即可分别求出、的值,然后再求出的值.
【详解】解:与互为相反数,而,
且,
∴,
解得,
,
.
故选:C.
【点睛】此题主要考查了二次根式的性质及函数解析式,利用二次根式的非负性确定、的值是解题的关键,然后代入数值计算即可解决问题.
4.C
【分析】根据变量与常量的定义分别判断,并选择正确的选项即可.
【详解】解:2与π为常量,C与r为变量,
故选:C.
【点睛】本题考查变量与常量的概念,能够熟练掌握变量与常量的概念为解决本题的关键.
5.A
【分析】根据等腰三角形周长公式可求出底边长与腰的函数关系式,由三角形两边之和大于第三边的关系可知的取值范围.
【详解】解:由题意可得:,
化简得:,
又由三角形两边之和大于第三边的关系可知:
,即,
解得:
故选:A.
【点睛】本题考查了根据实际问题列一次函数关系式、三角形的三边关系及等腰三角形的性质.正确列出函数解析式是解题的关键.
6.B
【分析】根据函数y=可得出x-5≥0,再解出一元一次不等式即可.
【详解】由题意得,x-5≥0,
解得x≥5.
在数轴上表示如下:
故选B.
【点睛】本题要考查的是一元一次不等式的解法以及二次根式成立得出判定,熟练掌握一元一次不等式的解法是本题的解题关键.
7.A
【分析】直接利用已知运算公式公式得出b的值,进而代入求出x=3时对应的值.
【详解】解:∵输入x的值是4时,输出的y的值为7,
∴7=2×4+b,
解得:b=-1,
若输入x的值是2,则输出的y的值是:y=-1×2+3=1.
故选:A.
【点睛】此题主要考查了函数值,正确得出b的值是解题关键.
8.D
【分析】根据表中数据表示出函数的解析式以及表格,两个变量之间的变化关系即可正确解答本题.
【详解】解:根据表格数据可以得出两个变量的关系式为y= x+18,
A、当x=14min时,y= 14+18=4mg,故选项不符合题意;
B、在一定范围内,燃烧时间越长,室内每立方米空气中的含药量越小,故选项不符合题意;
C、挥发时间每增加2min,室内每立方米空气中的含药量减少2mg,故选项不符合题意;
D、因为室内每立方米空气中的含药量随时间的变化而变化,所以时间是自变量,每立方米空气中的含药量是时间的函数,故选项符合题意.
故选:D.
【点睛】本题考查了函数的定义和性质,解题关键是能读懂表格中数据的特征,理解函数的定义.
9.C
【分析】水位随着水减少而下降,且饮水机是圆柱形,是同等变化的下降.
【详解】根据图片位置分析:水减少的体积随着水位下降的高度而增加,且饮水机是圆柱形,所以均匀增加
故答案选:C
【点睛】本题考查用图象法表示变量之间的关系,掌握变量之间的变化关系解题关键.
10.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
11.
【分析】由分母不为0结合被开方数为非负数可得,再解不等式组即可得到答案.
【详解】解:由题意得:
由①得:
由②得:
所以不等式组的解集为:
所以函数自变量x的取值范围是
故答案为:
【点睛】本题考查的是函数自变量的取值范围,二次根式有意义的条件,分式有意义的条件,掌握“求解函数自变量的取值范围的方法”是解本题的关键.
12.①②④.
【详解】在一个变化过程中,有两个变量x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为①②④.
13.或
【分析】将分别代入函数解析式,求出x的值,然后根据取值范围得出x的值.
【详解】解:当时,则时,
解得:,
∵,
∴;
当时,时,
解得:,符合题意,
∴综上所述:或.
故答案为:或.
【点睛】本题主要考查的是求解函数自变量值,属于基础题型.根据取值范围确定自变量的值是解题的关键.
14.
【分析】根据用水不超过立方米的收费标准、用水超过立方米时的收费标准分别得出与的函数关系式,然后根据确定与的关系式即可
【详解】解:由题意可得:每户每月应交水费元与用水量立方米之间的函数关系式为
,
因为月份用水量为立方米,应交水费元,则关于的函数表达式为;
故答案为:.
【点睛】本题主要考查了求函数关系式,掌握立方米这个分界点是解答本题的关键.
15.36或37
【分析】首先理解表示的含义,再结合得出中有多少个,多少个,然后求出的取值范围,即可求解;
【详解】,,
,,,等于0或1,
,
其中有18个1,
,,
,,
,
,
的值可以是36或37,
故答案为:36或37.
【点睛】本题主要考查取整函数的知识点,能够准确理解题意,得出一定的规律是解题的关键.
16. 增大 68.6
【分析】从表格可以看到y随x的增大而增大;根据距离=速度×时间即可求出这人到发令点的距离.
【详解】解:从表格可以看到y随x的增大而增大;
时,音速为343米/秒,米,
这个人距离发令点68.6米;
故答案为:增大;68.6.
【点睛】本题考查变量之间的关系,函数的表示方法;能够通过表格观察出变量的变化关系,利用表格的数据计算距离是解题的关键.
17.
【分析】用含的式子表示出的长,用矩形的面积公式表示出与的关系式即可.
【详解】解:由题意,得:,
∴,
即:;
∵,
∴,
∴;
故答案为:.
【点睛】本题考查求函数表达式.熟练掌握矩形的面积公式,是解题的关键.注意,自变量的取值范围.
18.
【分析】过作与点,设,则,根据等角的余角相等得到,易证得,所以,,得到,在中,根据勾股定理得到,所以有,即;根据四边形的面积三角形的面积三角形的面积,即可得到.
【详解】解:过作于点,如图,
设,则,
,,
∴,
,
而,,
∴,
,,
,
在中,由勾股定理得,
,即,
又四边形的面积三角形的面积三角形的面积,
.
故答案为.
【点睛】本题考查了三角形全等的判定与性质.也考查了勾股定理、函数解析式以及三角形的面积公式,解题的关键是三角形全等的判定与性质.
19.(1)13.5
(2)y=0.5x+12
(3)14.75cm
(4)16kg
【分析】(1)根据表格,找到所挂物体的质量为3kg时,弹簧的长度即可;
(2)由表格可知,质量每增加1kg,弹簧伸长0.5cm,确定y与x的关系式即可;
(3)将代入解析式,求出值,即可得解;
(4)将,代入解析式,求出的值,即可得解。
【详解】(1)解:由表可知当所挂物体的质量为3kg时,弹簧的长度是13.5,
故答案为:13.5;
(2)由表可知:弹簧原长为12cm,所挂物体每增加1kg弹簧伸长0.5cm,
∴弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式为;
(3)当kg时,代入,
解得cm,
即弹簧总长为14.75cm.
(4)当cm时,代入,
解得,
即所挂物体的质量为16kg.
【点睛】本题考查了函数的关系式及函数值,解题关键是根据表格信息列出解析式.
20.(1)所剪次数,正三角形个数;
(2)13;
(3);
(4)31
【分析】(1)根据表格中数的关系可以解答本题;
(2)根据表格中的数据可以解答本题;
(3)根据表格中的数据可以得到与n的关系式;
(4)根据(3)中的关系式可以解答本题.
【详解】(1)解:由表格可知,
所剪次数是自变量,正三角形个数是因变量,
故答案为:所剪次数,正三角形个数;
(2)由表格可知,
当所剪次数为4次时,正三角形的个数是13,
故答案为:13;
(3)由表格可得,
,
故答案为:;
(4)当时,,
故答案为:31.
【点睛】本题考查函数关系式、图形的变化类、常量与变量,解答本题的关键是明确函数的定义,利用函数的思想解答.
21.(1)这个表反映了超出时间与超出部分的电话费之间的关系,超出时间是自变量;
(2);
(3)需多付元电话费;
(4)小明的爸爸国内拨打电话超出36分钟.
【分析】(1)根据题意和表格可知,这个表反映了超出时间与超出部分的电话费之间的关系,
再根据超出部分的电话费随着超出时间的变化而变化,即可得出超出时间是自变量;
(2)根据超出部分国内拨打话元/分,据此即可得到y与x的关系式;
(3)将代入(2)所得关系式中进行计算,即可得到答案;
(4)将代入(2)所得关系式中进行计算,即可得到答案.
【详解】(1)解:由题意和表格可知,这个表反映了超出时间与超出部分的电话费之间的关系,
超出部分的电话费随着超出时间的变化而变化,
超出时间是自变量;
(2)解:超出部分国内拨打话费为元/分,
;
(3)解:当时,,
国内拨打电话超出10分钟,需多付元电话费;
(4)解:当时,,
解得:,
小明的爸爸国内拨打电话超出36分钟.
【点睛】本题考查了自变量、利用关系式表示变量之间的关系、求自变量的值或函数值,读懂题意,正确求出超出部分的电话费和超出时间之间的关系是解题关键.
22.(1)
(2)①;②此次活动该村获润不低于25000元,则最多销售箱苹果
【分析】(1)根据售价减去进价乘以数量即可求解;
(2)①根据售价减去进价乘以数量列出函数关系式即可求解;②根据题意列出不等式,即可求解.
【详解】(1)解:依题意(元);
故答案为:.
(2)解:设购进苹果m箱,则购进橙子箱,获得的利润为W元.
∴
∴
②依题意,,
解得:,
答:此次活动该村获润不低于25000元,则最多销售箱苹果
【点睛】本题考查了有理数的运算,列函数关系式,一元一次不等式的应用,根据题意列出关系式是解题的关键.
23.(1)销售一个外科口罩的原价为1元,优惠价为0.5元
(2)
(3)560元
【分析】(1)设销售一个外科口罩的原价为m元,优惠价为n元,根据小王家一次性买了外科口罩 90 个,花了 65 元;小李家一次性买了外科口罩 120 个, 花了 80 元列出方程组求解即可;
(2)分和两种情况求出对应的关系式即可;
(3)把代入(2)所求关系式中进行求解即可.
【详解】(1)解:设销售一个外科口罩的原价为m元,优惠价为n元,
由题意得,
解得,
∴销售一个外科口罩的原价为1元,优惠价为0.5元,
答:销售一个外科口罩的原价为1元,优惠价为0.5元;
(2)解:当时,;
当时,;
综上所述,;
(3)解:当时,元,
答:这个月学校一次性购买该外科口罩1080 个,花了560元.
【点睛】本题主要考查了二元一次方程组的实际应用,列函数关系式,求函数值,灵活运用所学知识是解题的关键.
24.(1)
(2)
【分析】(1)先证明得到,再根据平行四边形的性质得到,,再证明为等腰直角三角形,求出,由,得到,则;
(2)分当时,如图2所示,此时重叠部分面积为,当时,如图3所示,此时重叠面积为,聚餐求解即可
【详解】(1)解:∵为等腰直角三角形,,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∵四边形为平行四边形,
∴,,
当点M在边上时,如图1,
∵,
∴.
∵,
∴为等腰直角三角形,
∴,
∴,
∵,
∴,
∴.
(2)解:①当时,如图2,
∵四边形为平行四边形,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴;
②∵在中,.
∵,,
∴,
∴当时,如图3,
∵,
∴,
∵为等腰直角三角形,
∴.
∴,
∵,
∴,
∵,,
∴为等腰直角三角形,
∴,
∴,
综上所述,
【点睛】本题主要考查了等腰直角三角形的性质与判定,平行四边形的性质,列函数关系式,勾股定理,利用分类讨论的思想求解是解题的关键.
答案第14页,共14页
答案第13页,共14页
一、单选题
1.下列图像不能表示是的函数的是( )
A.B. C.D.
2.下列关系式中,y不是x的函数的是( )
A. B. C. D.
3.已知,那么的值是( )
A.-6 B.-9 C.9 D.6
4.水中涟漪(圆形水波)不断扩大,记它的半径为r,则圆周长C与r的关系式为.下列判断正确的是( )
A.2是变量 B.是变量 C.r是变量 D.C是常量
5.等腰三角形的周长是,腰长是底边长的函数,此函数解析式和自变量取值范围正确的是( )
A. B.
C. D.
6.函数y=中,自变量x的取值范围在数轴上表示正确的是( )
A. B.C. D.
7.根据如图所示的程序计算函数y的值,若输入x的值为4时,输出的y的值为7,则输入x的值为2时,输出的y的值为( )
A.1 B.2 C.4 D.5
8.为预防新冠肺炎,某校定期对教室进行消毒水消毒,测出药物喷洒后每立方米空气中的含药量y(mg)和时间x(min)的数据如表:
时间x(min) 2 4 6 8
含药量y(mg) 16 14 12 10
则下列叙述错误的是( )
A.时间为14min时,室内每立方米空气中的含药量为4mg
B.在一定范围内,时间越长,室内每立方米空气中的含药量越小
C.挥发时间每增加2min,室内每立方米空气中的含药量减少2mg
D.室内每立方米空气中的含药量是自变量
9.是饮水机的图片.饮水桶中的水由图1的位置下降到图2的位置的过程中,如果水减少的体积是y,水位下降的高度是x,那么能够表示y与x之间函数关系的图象可能是( )
A. B.
C. D.
10.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
二、填空题
11.函数自变量x的取值范围是 .
12.下列变量间的关系是函数关系的有 (填序号)
①正方形的周长与边长;②圆的面积与半径;
③;④商场中某种商品的单价为a元,销售总额与销售数量
13.若函数,则当函数值时,自变量的值为 .
14.为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过立方米时,水价为每立方米元;超过立方米时,超出部分按每立方米元收费,该市每户居民月份用水立方米,应交水费元,则与的关系式为 .
15.已知,且满足表示不超过的最大整数),则的值可以为 .
16.声音在空气中传播的速度y(米/秒)(简称音速)与气温之间的关系如下:
气温 0 5 10 15 20
音速y(米/秒) 331 334 337 340 343
从表中可知音速y随温度x的升高而 .在气温为的一天召开运动会,某人看到发令枪的烟0.2秒后,听到了枪声,则由此可知,这个人距发令地点 米.
17.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形的边长为,则矩形的面积与的关系式为 .
18.如图,在四边形中,,,,设的长为x,四边形的面积为y,则y与x之间的函数关系式为 .
三、解答题
19.探索计算:弹簧挂上物体后会伸长.已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如下表:
所挂物体的质量/kg 0 1 2 3 4 5 6 7
弹簧的长度/cm 12 12.5 13 13.5 14 14.5 15 15.5
(1)当所挂物体的质量为3kg时,弹簧的长度是 ;
(2)在弹性限度内如果所挂物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(3)当所挂物体的质量为5.5kg时,请求出弹簧的长度;
(4)如果弹簧的最大长度为20cm,那么该弹簧最多能挂质量为多少的物体?
20.如图,将一个正三角形纸片剪成四个全等的小正三角形,在将其中的一个按同样的方法剪成四个更小的正三角形,……,如此继续下去,结果如下表:
所剪次数 1 2 3 4 …
正三角形个数 4 7 10 13 …
(1)上表中自变量和因变量分别是___________.
(2)当所剪次数为4次时,正三角形的个数是___________
(3)求与的关系式:___________
(4)当所剪次数为10次时,求正三角形的个数___________.
21.开通了,中国联通公司公布了收费标准,其中包月129元时,超出部分国内拨打话元/分.由于业务多,小明的爸爸打电话已超出了包月费.下表是超出部分国内拨打的收费标准.
时间/分 1 2 3 4 5 …
电话费/元 …
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示国内拨打超出时间,y表示国内拨打超出部分的电话费,那么y与x的关系式是什么?
(3)如果国内拨打电话超出10分钟,需多付多少电话费?
(4)某次超出部分国内拨打电话的费用是元,那么小明的爸爸国内拨打电话超出几分钟?
22.为了帮助经济相对薄弱村发展经济,将真正的实惠带给消费者,某市在各菜市场开设了“爱心助农销售专区”.现从某村购进苹果和橙子进行销售,进价分别为每箱40元和60元,该专区决定苹果以每箱60元出售,橙子以每箱88元出售.
(1)若购进苹果120箱,橙子200箱,可获利______元;
(2)为满足市场需求,需购进这两种水果共1000箱,设购进苹果m箱,获得的利润为W元.
①请求出获利W(元)与购进苹果箱数m(箱)之间的函数表达式;
②若此次活动该村获润不低于25000元,则最多销售多少箱苹果?
23.防疫期间,某药店销售一批外科口罩,如果一次性购买 40 个以上的外科口罩,超过 40 个部分按优惠价出售.上个月小王家一次性买了外科口罩 90 个,花了 65 元;小李家一次性买了外科口罩 120 个, 花了 80 元.
(1)求销售一个外科口罩的原价和优惠价分别是多少?
(2)设一次性购买外科口罩 x 个,花费 y 元,写出 y 与 x 之间的函数关系式.
(3)这个月学校一次性购买该外科口罩1080 个,花了多少钱?
24.如图,在等腰中,,,,动点P以的速度从点B出发,沿边向终点C运动,过P作于点Q,以为邻边作平行四边形.设点P的运动时间为t(s),与重叠部分图形面积为.
(1)当点M落在边上时,求t的值;
(2)求S与t的函数关系,并直接写出自变量t的取值范围.
试卷第4页,共6页
试卷第3页,共6页
参考答案:
1.B
【分析】根据函数的图象可知对于x的每一个值y都有唯一的值与之相对应进行判定即可.
【详解】根据函数的概念:如果在一个变化过程中,有两个变量x、y,对于x的每一个值,y都有唯一确定的值与之对应,这时称y是x的函数.
选项B,对于一个x有两个y与之对应,故不是函数图象,
故选:B.
【点睛】本题主要考查了函数的图象,以及函数的表示方法,解题的关键是函数的定义,属于基础题.
2.C
【分析】根据函数的概念可知,满足对于x的每一个取值,y都有唯一确定的值与之对应关系,据此分析每一选项即可得出答案.
【详解】A. 符合函数定义,是函数,故选项错误,不符合题意;
B. 符合函数定义,是函数,故选项错误,不符合题意;
C. 对于x的每一个取值(),y都有两个值,不是函数,故选项正确,符合题意;
D. 符合函数定义,是函数,故选项错误,不符合题意.
故选:C
【点睛】本题考查了函数的定义,一般地,在一个变化过程中有两个变量x与y,对于x的每一个确定的值,y都有唯一的值与其对应,那么就说y是x的函数,x是自变量.
3.C
【分析】由于和中的被开方数互为相反数,根据二次根式的性质可以得到,由此即可分别求出、的值,然后再求出的值.
【详解】解:与互为相反数,而,
且,
∴,
解得,
,
.
故选:C.
【点睛】此题主要考查了二次根式的性质及函数解析式,利用二次根式的非负性确定、的值是解题的关键,然后代入数值计算即可解决问题.
4.C
【分析】根据变量与常量的定义分别判断,并选择正确的选项即可.
【详解】解:2与π为常量,C与r为变量,
故选:C.
【点睛】本题考查变量与常量的概念,能够熟练掌握变量与常量的概念为解决本题的关键.
5.A
【分析】根据等腰三角形周长公式可求出底边长与腰的函数关系式,由三角形两边之和大于第三边的关系可知的取值范围.
【详解】解:由题意可得:,
化简得:,
又由三角形两边之和大于第三边的关系可知:
,即,
解得:
故选:A.
【点睛】本题考查了根据实际问题列一次函数关系式、三角形的三边关系及等腰三角形的性质.正确列出函数解析式是解题的关键.
6.B
【分析】根据函数y=可得出x-5≥0,再解出一元一次不等式即可.
【详解】由题意得,x-5≥0,
解得x≥5.
在数轴上表示如下:
故选B.
【点睛】本题要考查的是一元一次不等式的解法以及二次根式成立得出判定,熟练掌握一元一次不等式的解法是本题的解题关键.
7.A
【分析】直接利用已知运算公式公式得出b的值,进而代入求出x=3时对应的值.
【详解】解:∵输入x的值是4时,输出的y的值为7,
∴7=2×4+b,
解得:b=-1,
若输入x的值是2,则输出的y的值是:y=-1×2+3=1.
故选:A.
【点睛】此题主要考查了函数值,正确得出b的值是解题关键.
8.D
【分析】根据表中数据表示出函数的解析式以及表格,两个变量之间的变化关系即可正确解答本题.
【详解】解:根据表格数据可以得出两个变量的关系式为y= x+18,
A、当x=14min时,y= 14+18=4mg,故选项不符合题意;
B、在一定范围内,燃烧时间越长,室内每立方米空气中的含药量越小,故选项不符合题意;
C、挥发时间每增加2min,室内每立方米空气中的含药量减少2mg,故选项不符合题意;
D、因为室内每立方米空气中的含药量随时间的变化而变化,所以时间是自变量,每立方米空气中的含药量是时间的函数,故选项符合题意.
故选:D.
【点睛】本题考查了函数的定义和性质,解题关键是能读懂表格中数据的特征,理解函数的定义.
9.C
【分析】水位随着水减少而下降,且饮水机是圆柱形,是同等变化的下降.
【详解】根据图片位置分析:水减少的体积随着水位下降的高度而增加,且饮水机是圆柱形,所以均匀增加
故答案选:C
【点睛】本题考查用图象法表示变量之间的关系,掌握变量之间的变化关系解题关键.
10.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
11.
【分析】由分母不为0结合被开方数为非负数可得,再解不等式组即可得到答案.
【详解】解:由题意得:
由①得:
由②得:
所以不等式组的解集为:
所以函数自变量x的取值范围是
故答案为:
【点睛】本题考查的是函数自变量的取值范围,二次根式有意义的条件,分式有意义的条件,掌握“求解函数自变量的取值范围的方法”是解本题的关键.
12.①②④.
【详解】在一个变化过程中,有两个变量x和y,对于x的每一个确定值,y都有唯一的值与之对应,则称y是x的函数,在③中,当x取一个值时,对应的y值有两个,故不是函数,
故答案为①②④.
13.或
【分析】将分别代入函数解析式,求出x的值,然后根据取值范围得出x的值.
【详解】解:当时,则时,
解得:,
∵,
∴;
当时,时,
解得:,符合题意,
∴综上所述:或.
故答案为:或.
【点睛】本题主要考查的是求解函数自变量值,属于基础题型.根据取值范围确定自变量的值是解题的关键.
14.
【分析】根据用水不超过立方米的收费标准、用水超过立方米时的收费标准分别得出与的函数关系式,然后根据确定与的关系式即可
【详解】解:由题意可得:每户每月应交水费元与用水量立方米之间的函数关系式为
,
因为月份用水量为立方米,应交水费元,则关于的函数表达式为;
故答案为:.
【点睛】本题主要考查了求函数关系式,掌握立方米这个分界点是解答本题的关键.
15.36或37
【分析】首先理解表示的含义,再结合得出中有多少个,多少个,然后求出的取值范围,即可求解;
【详解】,,
,,,等于0或1,
,
其中有18个1,
,,
,,
,
,
的值可以是36或37,
故答案为:36或37.
【点睛】本题主要考查取整函数的知识点,能够准确理解题意,得出一定的规律是解题的关键.
16. 增大 68.6
【分析】从表格可以看到y随x的增大而增大;根据距离=速度×时间即可求出这人到发令点的距离.
【详解】解:从表格可以看到y随x的增大而增大;
时,音速为343米/秒,米,
这个人距离发令点68.6米;
故答案为:增大;68.6.
【点睛】本题考查变量之间的关系,函数的表示方法;能够通过表格观察出变量的变化关系,利用表格的数据计算距离是解题的关键.
17.
【分析】用含的式子表示出的长,用矩形的面积公式表示出与的关系式即可.
【详解】解:由题意,得:,
∴,
即:;
∵,
∴,
∴;
故答案为:.
【点睛】本题考查求函数表达式.熟练掌握矩形的面积公式,是解题的关键.注意,自变量的取值范围.
18.
【分析】过作与点,设,则,根据等角的余角相等得到,易证得,所以,,得到,在中,根据勾股定理得到,所以有,即;根据四边形的面积三角形的面积三角形的面积,即可得到.
【详解】解:过作于点,如图,
设,则,
,,
∴,
,
而,,
∴,
,,
,
在中,由勾股定理得,
,即,
又四边形的面积三角形的面积三角形的面积,
.
故答案为.
【点睛】本题考查了三角形全等的判定与性质.也考查了勾股定理、函数解析式以及三角形的面积公式,解题的关键是三角形全等的判定与性质.
19.(1)13.5
(2)y=0.5x+12
(3)14.75cm
(4)16kg
【分析】(1)根据表格,找到所挂物体的质量为3kg时,弹簧的长度即可;
(2)由表格可知,质量每增加1kg,弹簧伸长0.5cm,确定y与x的关系式即可;
(3)将代入解析式,求出值,即可得解;
(4)将,代入解析式,求出的值,即可得解。
【详解】(1)解:由表可知当所挂物体的质量为3kg时,弹簧的长度是13.5,
故答案为:13.5;
(2)由表可知:弹簧原长为12cm,所挂物体每增加1kg弹簧伸长0.5cm,
∴弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式为;
(3)当kg时,代入,
解得cm,
即弹簧总长为14.75cm.
(4)当cm时,代入,
解得,
即所挂物体的质量为16kg.
【点睛】本题考查了函数的关系式及函数值,解题关键是根据表格信息列出解析式.
20.(1)所剪次数,正三角形个数;
(2)13;
(3);
(4)31
【分析】(1)根据表格中数的关系可以解答本题;
(2)根据表格中的数据可以解答本题;
(3)根据表格中的数据可以得到与n的关系式;
(4)根据(3)中的关系式可以解答本题.
【详解】(1)解:由表格可知,
所剪次数是自变量,正三角形个数是因变量,
故答案为:所剪次数,正三角形个数;
(2)由表格可知,
当所剪次数为4次时,正三角形的个数是13,
故答案为:13;
(3)由表格可得,
,
故答案为:;
(4)当时,,
故答案为:31.
【点睛】本题考查函数关系式、图形的变化类、常量与变量,解答本题的关键是明确函数的定义,利用函数的思想解答.
21.(1)这个表反映了超出时间与超出部分的电话费之间的关系,超出时间是自变量;
(2);
(3)需多付元电话费;
(4)小明的爸爸国内拨打电话超出36分钟.
【分析】(1)根据题意和表格可知,这个表反映了超出时间与超出部分的电话费之间的关系,
再根据超出部分的电话费随着超出时间的变化而变化,即可得出超出时间是自变量;
(2)根据超出部分国内拨打话元/分,据此即可得到y与x的关系式;
(3)将代入(2)所得关系式中进行计算,即可得到答案;
(4)将代入(2)所得关系式中进行计算,即可得到答案.
【详解】(1)解:由题意和表格可知,这个表反映了超出时间与超出部分的电话费之间的关系,
超出部分的电话费随着超出时间的变化而变化,
超出时间是自变量;
(2)解:超出部分国内拨打话费为元/分,
;
(3)解:当时,,
国内拨打电话超出10分钟,需多付元电话费;
(4)解:当时,,
解得:,
小明的爸爸国内拨打电话超出36分钟.
【点睛】本题考查了自变量、利用关系式表示变量之间的关系、求自变量的值或函数值,读懂题意,正确求出超出部分的电话费和超出时间之间的关系是解题关键.
22.(1)
(2)①;②此次活动该村获润不低于25000元,则最多销售箱苹果
【分析】(1)根据售价减去进价乘以数量即可求解;
(2)①根据售价减去进价乘以数量列出函数关系式即可求解;②根据题意列出不等式,即可求解.
【详解】(1)解:依题意(元);
故答案为:.
(2)解:设购进苹果m箱,则购进橙子箱,获得的利润为W元.
∴
∴
②依题意,,
解得:,
答:此次活动该村获润不低于25000元,则最多销售箱苹果
【点睛】本题考查了有理数的运算,列函数关系式,一元一次不等式的应用,根据题意列出关系式是解题的关键.
23.(1)销售一个外科口罩的原价为1元,优惠价为0.5元
(2)
(3)560元
【分析】(1)设销售一个外科口罩的原价为m元,优惠价为n元,根据小王家一次性买了外科口罩 90 个,花了 65 元;小李家一次性买了外科口罩 120 个, 花了 80 元列出方程组求解即可;
(2)分和两种情况求出对应的关系式即可;
(3)把代入(2)所求关系式中进行求解即可.
【详解】(1)解:设销售一个外科口罩的原价为m元,优惠价为n元,
由题意得,
解得,
∴销售一个外科口罩的原价为1元,优惠价为0.5元,
答:销售一个外科口罩的原价为1元,优惠价为0.5元;
(2)解:当时,;
当时,;
综上所述,;
(3)解:当时,元,
答:这个月学校一次性购买该外科口罩1080 个,花了560元.
【点睛】本题主要考查了二元一次方程组的实际应用,列函数关系式,求函数值,灵活运用所学知识是解题的关键.
24.(1)
(2)
【分析】(1)先证明得到,再根据平行四边形的性质得到,,再证明为等腰直角三角形,求出,由,得到,则;
(2)分当时,如图2所示,此时重叠部分面积为,当时,如图3所示,此时重叠面积为,聚餐求解即可
【详解】(1)解:∵为等腰直角三角形,,
∴,
∵,
∴,
∴,
∴.
∵,
∴,
∴,
∵四边形为平行四边形,
∴,,
当点M在边上时,如图1,
∵,
∴.
∵,
∴为等腰直角三角形,
∴,
∴,
∵,
∴,
∴.
(2)解:①当时,如图2,
∵四边形为平行四边形,
∴,,
∴,
∴为等腰直角三角形,
∴,
∴;
②∵在中,.
∵,,
∴,
∴当时,如图3,
∵,
∴,
∵为等腰直角三角形,
∴.
∴,
∵,
∴,
∵,,
∴为等腰直角三角形,
∴,
∴,
综上所述,
【点睛】本题主要考查了等腰直角三角形的性质与判定,平行四边形的性质,列函数关系式,勾股定理,利用分类讨论的思想求解是解题的关键.
答案第14页,共14页
答案第13页,共14页
