三角形的外角(广西壮族自治区梧州市)
文档属性
| 名称 | 三角形的外角(广西壮族自治区梧州市) |  | |
| 格式 | rar | ||
| 文件大小 | 175.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-15 13:53:00 | ||
图片预览



文档简介
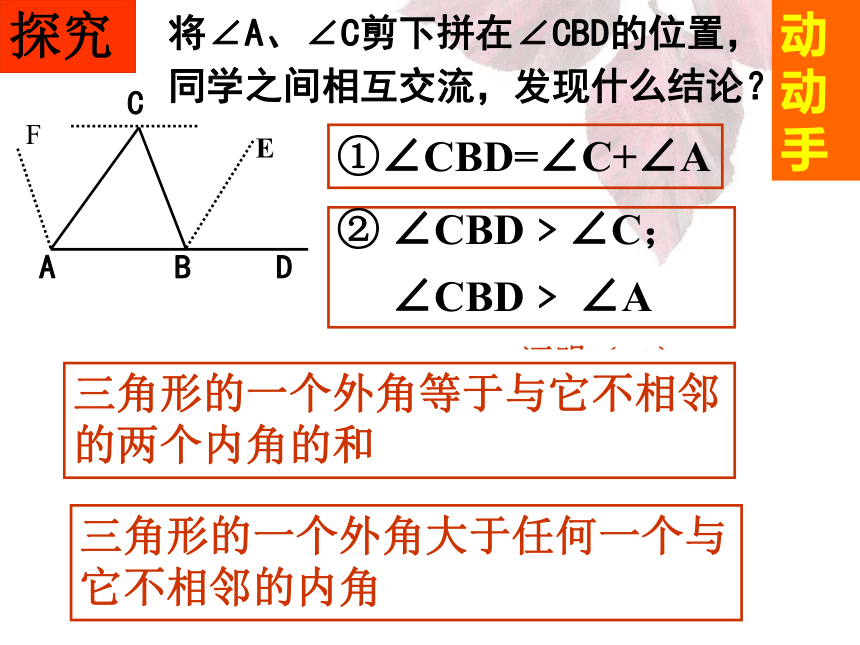
课件12张PPT。三角形的外角外角3、三角形外角与内角的关系(1)位置关系(2)数量关系外角+相邻的内角=180 ?(互补)相邻的内角不相邻的内角1、什么是三角形的内角?其和等于多少?复习2、什么是三角形的外角?思考三角形的外角与它不相邻的内角之间有什么关系呢?探究①∠CBD=∠C+∠A将∠A、∠C剪下拼在∠CBD的位置,
同学之间相互交流,发现什么结论?动动手E∵ ∠ABC + ∠CBD= 180 °又∵ ∠ABC+ ∠C+ ∠A= 180 °∴ ∠CBD= ∠C+ ∠A证明(一)证明(二):过B点作 BE∥AC∴ ∠EBD = ∠A ( ? )∠CBE = ∠C ( ? )∴ ∠CBD = ∠CBE+ ∠EBD= ∠C+ ∠AF② ∠CBD﹥∠C;
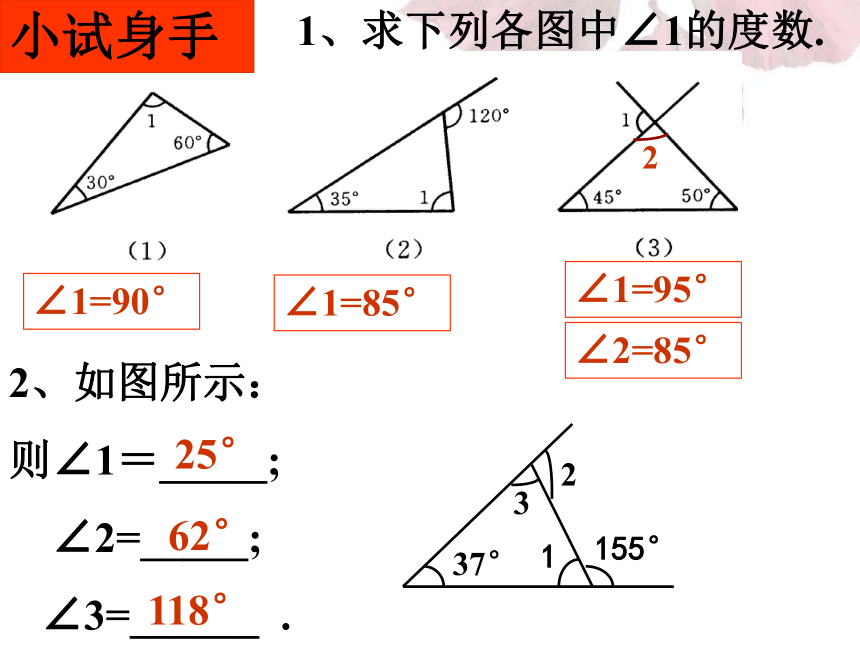
∠CBD﹥ ∠A三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角大于任何一个与它不相邻的内角 1、求下列各图中∠1的度数.小试身手2∠1=90°∠1=85°∠1=95°∠2=85°2、如图所示:
则∠1=_____;
∠2=_____;
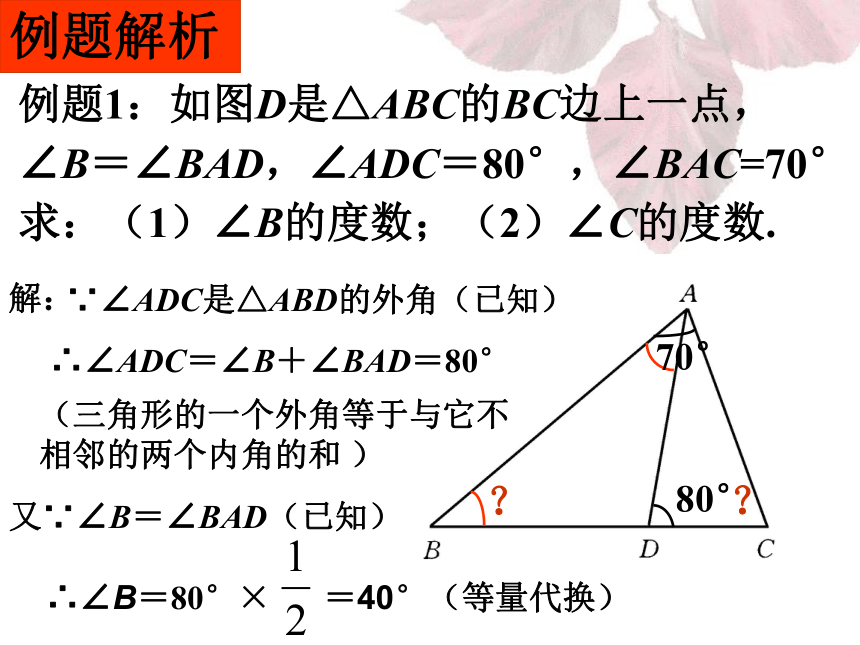
∠3=______ . 25°62°118°小试身手3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______30°例题解析例题1:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.80°70°??∵∠ADC是△ABD的外角(已知) 解:∴∠ADC=∠B+∠BAD=80° 又∵∠B=∠BAD(已知) (三角形的一个外角等于与它不
相邻的两个内角的和 )1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:______________________.∠A< ∠2< ∠1求证: ∠A<∠1一题多变20°30°51°若∠ABP=20°, ∠ACP=30°, ∠A=51°,
求∠1的度数?思维提升1、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?12解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°课堂小结1、三角形内角和为180°;2、三角形外角的性质:(1)三角形的一个外角等于与它不相邻 的两个内角的和(2)三角形的一个外角大于任何一个与它不相邻的内角提高作业1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______提高作业1、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?提高作业如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
同学之间相互交流,发现什么结论?动动手E∵ ∠ABC + ∠CBD= 180 °又∵ ∠ABC+ ∠C+ ∠A= 180 °∴ ∠CBD= ∠C+ ∠A证明(一)证明(二):过B点作 BE∥AC∴ ∠EBD = ∠A ( ? )∠CBE = ∠C ( ? )∴ ∠CBD = ∠CBE+ ∠EBD= ∠C+ ∠AF② ∠CBD﹥∠C;
∠CBD﹥ ∠A三角形的一个外角等于与它不相邻的两个内角的和三角形的一个外角大于任何一个与它不相邻的内角 1、求下列各图中∠1的度数.小试身手2∠1=90°∠1=85°∠1=95°∠2=85°2、如图所示:
则∠1=_____;
∠2=_____;
∠3=______ . 25°62°118°小试身手3、如图:∠1=25°,∠2=95°,∠3=30°,则∠4=_______30°例题解析例题1:如图D是△ABC的BC边上一点,
∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.80°70°??∵∠ADC是△ABD的外角(已知) 解:∴∠ADC=∠B+∠BAD=80° 又∵∠B=∠BAD(已知) (三角形的一个外角等于与它不
相邻的两个内角的和 )1、如图:P是△ABC内的一点,延长BP交AC于点D,用“<”表示∠1、∠2、∠A的大小关系:______________________.∠A< ∠2< ∠1求证: ∠A<∠1一题多变20°30°51°若∠ABP=20°, ∠ACP=30°, ∠A=51°,
求∠1的度数?思维提升1、如图所示:求∠A+∠B+∠C+∠D+∠E
的度数?12解:∵∠1= ∠A+ ∠D(三角形的外角等于与它不相邻的两内角的和)又∵∠2= ∠B+ ∠E(三角形的外角等于与它不相邻的两内角的和)∴ ∠A+∠B+∠C+∠D+∠E=(∠A+ ∠D)+(∠B+ ∠E)+∠C=∠1+∠2+∠C=180°课堂小结1、三角形内角和为180°;2、三角形外角的性质:(1)三角形的一个外角等于与它不相邻 的两个内角的和(2)三角形的一个外角大于任何一个与它不相邻的内角提高作业1、将一副三角板按如图方式放置,则两条
斜边所形成的钝角∠1=______提高作业1、 △ABC中,BE为∠ABC的平分线,CE为∠ACD的平分线,两线交于E点。你能找出∠E与∠A有什么关系吗?提高作业如图所示, △ABC的高BD、CE交于H点,∠A=50°,求∠BHC的度数?
