数学人教A版(2019)必修第一册 5.1.1任意角 课件(共30张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册 5.1.1任意角 课件(共30张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 9.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 10:18:26 | ||
图片预览








文档简介
(共30张PPT)
第五章 三角函数
5.1.1 任意角
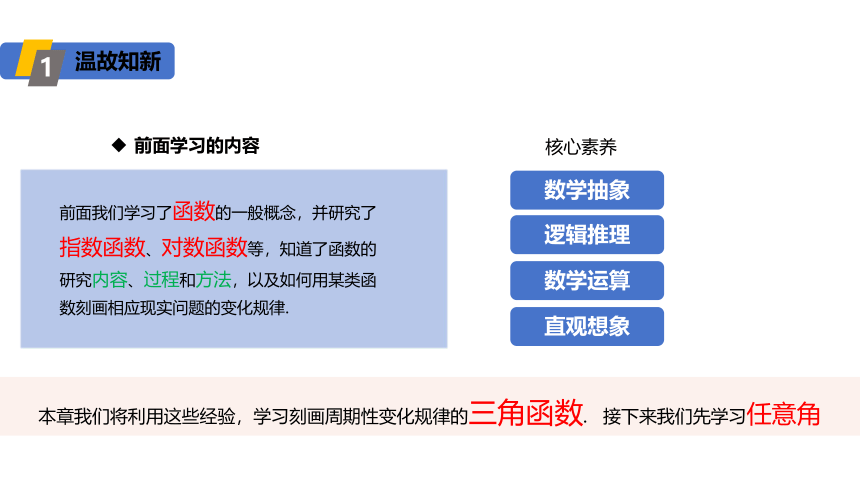
温故知新
1
前面学习的内容
前面我们学习了函数的一般概念,并研究了指数函数、对数函数等,知道了函数的研究内容、过程和方法,以及如何用某类函数刻画相应现实问题的变化规律.
数学抽象
核心素养
数学运算
逻辑推理
直观想象
本章我们将利用这些经验,学习刻画周期性变化规律的三角函数. 接下来我们先学习任意角
课标要求
1
重点
1.掌握用“旋转”定义角的概念,理解任意角的概念.
2.学会在平面内建立适当的坐标系来讨论角;并进而理解“正角”“负角”“象限角”“终边相同的角”的含义.
难点
3.掌握终边相同角的表示方法,会用角的集合表示一些实际问题中的角.
情景引入
2
情景一
以
前
学
习
的
角
情景引入
2
情景二
在跳水比赛中,运动员会做出“转体两周”“向前翻转两周半”等动作,做上述动作时,运动员转体多少度?转过的度数还能用0°到360°的角度表示吗?
提示 顺时针旋转720°或逆时针旋转720°.“向前翻转两周半”指顺时针或逆时针旋转900°,转的角度不能用0°到360°的角表示.
情景引入
2
问题1:任意角的概念是什么?
问题2:象限角的概念是什么?
问题3:终边相同的角怎么表示?
1
3
2
思考问题
1
2
初中学习的角
3
任意角的概念
任意角的理解
问题1
任意角的概念是什么?
讲解新课
3
讲解新课
3
初中学习的角
1
由初中知识可知,射线OA绕端点O 按逆时针方向旋转一周回到起始位置,在这个过程中可以得到0°~360°范围内的角.如果继续旋转,那么所得到的角就超出这个范围了,所以,为了借助角的大小变化刻画圆周运动,需要先扩大角的范围.
讲解新课
3
任意角的概念
2
现实生活中随处可见超出0°~360°范围的角,例如,体操中有“前空翻转体540度”"后空翻转体720度"这样的动作名称,这里不仅有超出0°~360°范围的角,而且旋转的方向也不相同;又如,图5.1-2是两个齿轮旋转的示意图,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮有相反的旋转方向,这样,OA 绕点O 旋转所成的角与O'B 绕 点O '旋转所成的角就会有不同的方向. 因此,要准确地描述这些现象,不仅要知道旋转的度数,还要知道旋转的方向,这就需要对角的概念进行推广.
被动轮 主动轮
讲解新课
3
任意角的概念
2
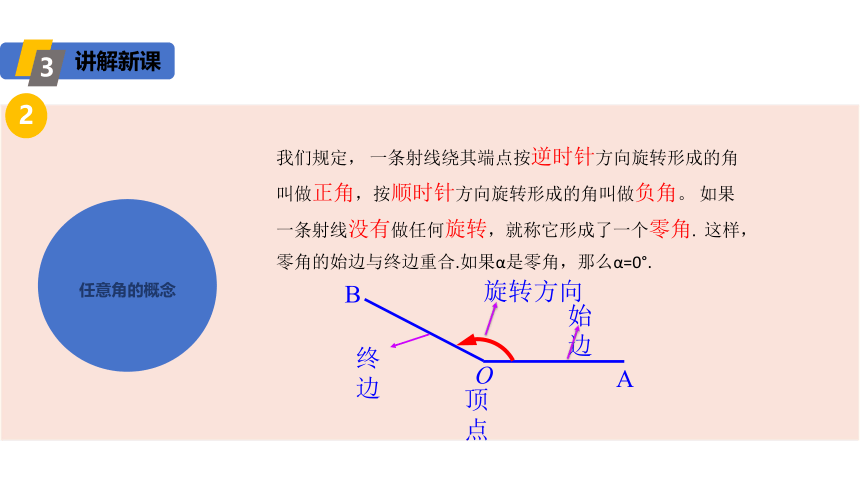
我们规定, 一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角。 如果一条射线没有做任何旋转,就称它形成了一个零角. 这样,零角的始边与终边重合.如果α是零角,那么α=0°.
始边
终边
顶点
A
B
O
旋转方向
讲解新课
3
任意角的概念
2
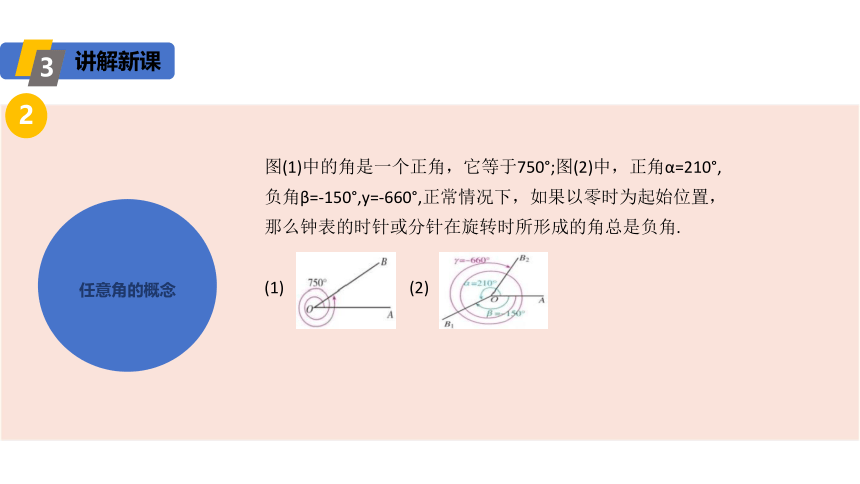
图(1)中的角是一个正角,它等于750°;图(2)中,正角α=210°,负角β=-150°,y=-660°,正常情况下,如果以零时为起始位置,那么钟表的时针或分针在旋转时所形成的角总是负角.
(1) (2)
讲解新课
3
任意角的概念
2
这样,我们就把角的概念推广到了任意角.
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角
任
意
角
规定:
讲解新课
3
任意角的概念
2
设角α由射线OA 绕端点O 旋转而成,角β由射线O'A '绕端点O '旋转而成.如果它们的旋转方向相同且旋转量相等,那么就称α=β.
设α,β 是任意两个角。我们规定,把角α的终边旋转角β,这时终边所对应的角是 α+β.
类似于实数a 的相反数是-a, 我们引入任意角α的相反角的概念.如图,我们把射线OA 绕端点O 按不同方向旋转相同的量所成的两个角叫做互为相反角。角α的相反 角记为-α. 于是,像实数减法的“减去一个数等于加上这个数的相反数”一样,我们有α- β=α+(一 β).
这样,角的减法可以转化为角的加法.
讲解新课
3
任意角的理解
3
1.任意角包括正角、负角和零角,角的范围不再限于0°~360°.
2.角的概念包含的三要素有:顶点、始边和终边.
1
象限角的概念
2
象限角的理解
问题2
象限角的概念是什么?
讲解新课
3
讲解新课
3
象限角的概念
1
我们通常在直角坐标系内讨论角。为了方便,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合. 那么,角的终边在第几象限,就说这个角是第几象限角.例如,图中的30°角、 -120°角分别是第一象限角和第三象限角.
o
y
x
讲解新课
3
象限角的理解
2
如果角的终边在坐标轴上,那么 就认为这个角不属于任何一个象限.
锐角一定是第一象限角,第一象限角不一定是锐角.
钝角一定是第二象限角,第二象限角不一定是钝角.
o
y
x
1
2
终边相同角的含义
3
终边相同角的表示
终边相同角的理解
问题3
终边相同的角怎么表示?
讲解新课
3
讲解新课
3
终边相同
角的含义
1
探究:
将角按照上述方法放在直角坐标系中后,给定一个角, 就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线 OB (如图),以它为终边的角是否唯一 如果不唯一,那么终边相同的角有什么关系
-32°
-392°
x
y
o
328°
讲解新课
3
终边相同
角的含义
1
不难发现,在图中,如果-32°角的终边是OB, 那么328°,-392°,…角的终边都是OB, 并且与-32°角终边相同的这些角都可以表示成-32°的角与k 个(k∈Z) 周角 的和,如
328°=-32°+360°(这里 k=1),
-392°=-32°-360°(这里k= -1).
设S={β | β=-32°+k ·360°,k∈Z}, 则328°,-392° 角都是S 的元素, -32°角也是S 的元素(此时k= 1). 因 此,所有与-32°角终边相同的角,连同-32°角在内,都是 集合S 的元素;反过来,集合S 的任一元素显然与-32°角的终边相同.
讲解新课
3
终边相同
角的表示
2
一般地,我们有:
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β |β=α+k · 360°,k ∈Z),
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
讲解新课
3
终边相同
角的理解
3
1.终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍.
2.利用终边相同的角的一般形式可以求出符合某些条件的终边相同的角,注意“k∈Z”这一条件.
例题讲解
4
(人教A版2019)
例1
在0°~360°范围内,找出与-950°12'角终边相同 的角,并判定它是第几象限角.
核心素养:数学运算
解析
—950°12'=129°48'-3×360°,所以在0°~360°范围内,与-950°12'角终边相同的角是129°48',它是第二象限角.
例题讲解
4
(人教A版2019)
例2
写出终边在y 轴上的角的集合.
核心素养:直观想象
解析
在0°~360°范围内,终边在y 轴上的角有两个,即 90°,270°角(如图),因此,所有与90°角终边相同的角构成集合
S ={β |β=90°+k · 360°,k ∈Z},
而所有与270°角终边相同的角构成集合
S ={β |β=270°+k · 360°,k ∈Z},
于是,终边在y 轴上的角的集合
S=S US
={β |β=90°+2k · 180°,k ∈Z}U{β |β=90°+180°+2k · 180°,k ∈Z} ={β |β=90°+2k · 180°,k ∈Z}U{β |β=90°+(2k+1)180°,k ∈Z}
={β |β=90°+n · 180°,n ∈Z}.
例题讲解
4
(人教A版2019)
例3
写出终边在直线y=x 上的角的集合S.S中满足不等
式-360°≤β<720°的元素β有哪些
核心素养:数学运算
解析
如图,在直角坐标系中画出直线y=x,可以发现
它与x 轴的夹角是45°,在0°~360°范围内,终边在直线y=x 上的角有两个:45°,225°。因此,终边在直线y=x 上的角的集合
S={β |β=45°+k · 360°,k ∈Z}U{β |β=225°+k · 360°,k ∈Z}
={β |β=45°+n · 180°,n ∈Z}.
S 中适合不等式-360°≤β<720°的元素β有
45°-2×180°=—315°,
45°-1×180°=—135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
课堂练习
5
【解析】
终边落在第一象限的角不一定是锐角,如400°的角是第一象限角,但不是锐角,故①的说法是错误的;
同理第二象限角也不一定是钝角,故③的说法也是错误的.
下列说法中,正确的是______(填序号).
①终边落在第一象限的角为锐角; ②锐角是第一象限角;
③第二象限角为钝角; ④角α与-α的终边关于x轴对称.
【训练1】
课堂练习
5
【解析】
因为-1 845°=-45°+(-5)×360°,
所以-1 845°角与-45°角的终边相同.
所以与角α终边相同的角的集合是{β|β=-45°+k·360°,k∈Z}.
(1)最小的正角为315°.
(2)最大的负角为-45°.
(3)-360°~720°之间的角分别是-45°,315°,675°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(1)最小的正角;(2)最大的负角;(3)-360°~720°之间的角.
【训练2】
课堂练习
5
【解析】
直角不属于任何一个象限,故A不正确;
120°是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
270°的终边在y轴上,它不属于任何一个象限,故D正确.
故选BD.
(多选)下列叙述正确的是( )
A.三角形的内角是第一象限角或第二象限角 B.120°是第二象限角
C.第二象限角比第一象限角大 D.270°不属于任何一个象限
【训练3】
课堂小结
6
1.总结一下本节课我们做了什么?你获得了哪些知识?
2.本节课的知识点总结.
3.你对本节课知识的理解是什么?
任意角
核心知识
方法总结
易错提醒
核心素养
角的概念、表示及分类
象限角
终边相同的角
象限角的两种判断方法:(1)化成终边相同角的表示形式;(2)在坐标系中画出相应的角,观察终边的位置
求在给定范围内终边相同角的方法:写出终边相同的角的表示,根据给定范围建立关于k的不等式,解出k,根据k确定角
终边相同的角中必须保证k是整数
数学抽象:通过具体实例抽象出象限角、终边相同角的概念,培养数学抽象的核心素养
课后作业
7
1. 思考:今天是星期三,那么7k(k∈Z)天后的那一天是星期几
7k(k∈Z)天前的那一天是星期几 100天后的那一天是星期几 ;
2. 完成课本171页 3,4,5
必做
3. 完成课本175页复习巩固1,2
选做
第五章 三角函数
5.1.1 任意角
温故知新
1
前面学习的内容
前面我们学习了函数的一般概念,并研究了指数函数、对数函数等,知道了函数的研究内容、过程和方法,以及如何用某类函数刻画相应现实问题的变化规律.
数学抽象
核心素养
数学运算
逻辑推理
直观想象
本章我们将利用这些经验,学习刻画周期性变化规律的三角函数. 接下来我们先学习任意角
课标要求
1
重点
1.掌握用“旋转”定义角的概念,理解任意角的概念.
2.学会在平面内建立适当的坐标系来讨论角;并进而理解“正角”“负角”“象限角”“终边相同的角”的含义.
难点
3.掌握终边相同角的表示方法,会用角的集合表示一些实际问题中的角.
情景引入
2
情景一
以
前
学
习
的
角
情景引入
2
情景二
在跳水比赛中,运动员会做出“转体两周”“向前翻转两周半”等动作,做上述动作时,运动员转体多少度?转过的度数还能用0°到360°的角度表示吗?
提示 顺时针旋转720°或逆时针旋转720°.“向前翻转两周半”指顺时针或逆时针旋转900°,转的角度不能用0°到360°的角表示.
情景引入
2
问题1:任意角的概念是什么?
问题2:象限角的概念是什么?
问题3:终边相同的角怎么表示?
1
3
2
思考问题
1
2
初中学习的角
3
任意角的概念
任意角的理解
问题1
任意角的概念是什么?
讲解新课
3
讲解新课
3
初中学习的角
1
由初中知识可知,射线OA绕端点O 按逆时针方向旋转一周回到起始位置,在这个过程中可以得到0°~360°范围内的角.如果继续旋转,那么所得到的角就超出这个范围了,所以,为了借助角的大小变化刻画圆周运动,需要先扩大角的范围.
讲解新课
3
任意角的概念
2
现实生活中随处可见超出0°~360°范围的角,例如,体操中有“前空翻转体540度”"后空翻转体720度"这样的动作名称,这里不仅有超出0°~360°范围的角,而且旋转的方向也不相同;又如,图5.1-2是两个齿轮旋转的示意图,被动轮随着主动轮的旋转而旋转,而且被动轮与主动轮有相反的旋转方向,这样,OA 绕点O 旋转所成的角与O'B 绕 点O '旋转所成的角就会有不同的方向. 因此,要准确地描述这些现象,不仅要知道旋转的度数,还要知道旋转的方向,这就需要对角的概念进行推广.
被动轮 主动轮
讲解新课
3
任意角的概念
2
我们规定, 一条射线绕其端点按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角。 如果一条射线没有做任何旋转,就称它形成了一个零角. 这样,零角的始边与终边重合.如果α是零角,那么α=0°.
始边
终边
顶点
A
B
O
旋转方向
讲解新课
3
任意角的概念
2
图(1)中的角是一个正角,它等于750°;图(2)中,正角α=210°,负角β=-150°,y=-660°,正常情况下,如果以零时为起始位置,那么钟表的时针或分针在旋转时所形成的角总是负角.
(1) (2)
讲解新课
3
任意角的概念
2
这样,我们就把角的概念推广到了任意角.
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角
任
意
角
规定:
讲解新课
3
任意角的概念
2
设角α由射线OA 绕端点O 旋转而成,角β由射线O'A '绕端点O '旋转而成.如果它们的旋转方向相同且旋转量相等,那么就称α=β.
设α,β 是任意两个角。我们规定,把角α的终边旋转角β,这时终边所对应的角是 α+β.
类似于实数a 的相反数是-a, 我们引入任意角α的相反角的概念.如图,我们把射线OA 绕端点O 按不同方向旋转相同的量所成的两个角叫做互为相反角。角α的相反 角记为-α. 于是,像实数减法的“减去一个数等于加上这个数的相反数”一样,我们有α- β=α+(一 β).
这样,角的减法可以转化为角的加法.
讲解新课
3
任意角的理解
3
1.任意角包括正角、负角和零角,角的范围不再限于0°~360°.
2.角的概念包含的三要素有:顶点、始边和终边.
1
象限角的概念
2
象限角的理解
问题2
象限角的概念是什么?
讲解新课
3
讲解新课
3
象限角的概念
1
我们通常在直角坐标系内讨论角。为了方便,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合. 那么,角的终边在第几象限,就说这个角是第几象限角.例如,图中的30°角、 -120°角分别是第一象限角和第三象限角.
o
y
x
讲解新课
3
象限角的理解
2
如果角的终边在坐标轴上,那么 就认为这个角不属于任何一个象限.
锐角一定是第一象限角,第一象限角不一定是锐角.
钝角一定是第二象限角,第二象限角不一定是钝角.
o
y
x
1
2
终边相同角的含义
3
终边相同角的表示
终边相同角的理解
问题3
终边相同的角怎么表示?
讲解新课
3
讲解新课
3
终边相同
角的含义
1
探究:
将角按照上述方法放在直角坐标系中后,给定一个角, 就有唯一的一条终边与之对应.反之,对于直角坐标系内任意一条射线 OB (如图),以它为终边的角是否唯一 如果不唯一,那么终边相同的角有什么关系
-32°
-392°
x
y
o
328°
讲解新课
3
终边相同
角的含义
1
不难发现,在图中,如果-32°角的终边是OB, 那么328°,-392°,…角的终边都是OB, 并且与-32°角终边相同的这些角都可以表示成-32°的角与k 个(k∈Z) 周角 的和,如
328°=-32°+360°(这里 k=1),
-392°=-32°-360°(这里k= -1).
设S={β | β=-32°+k ·360°,k∈Z}, 则328°,-392° 角都是S 的元素, -32°角也是S 的元素(此时k= 1). 因 此,所有与-32°角终边相同的角,连同-32°角在内,都是 集合S 的元素;反过来,集合S 的任一元素显然与-32°角的终边相同.
讲解新课
3
终边相同
角的表示
2
一般地,我们有:
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β |β=α+k · 360°,k ∈Z),
即任一与角α终边相同的角,都可以表示成角α与整数个周角的和.
讲解新课
3
终边相同
角的理解
3
1.终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍.
2.利用终边相同的角的一般形式可以求出符合某些条件的终边相同的角,注意“k∈Z”这一条件.
例题讲解
4
(人教A版2019)
例1
在0°~360°范围内,找出与-950°12'角终边相同 的角,并判定它是第几象限角.
核心素养:数学运算
解析
—950°12'=129°48'-3×360°,所以在0°~360°范围内,与-950°12'角终边相同的角是129°48',它是第二象限角.
例题讲解
4
(人教A版2019)
例2
写出终边在y 轴上的角的集合.
核心素养:直观想象
解析
在0°~360°范围内,终边在y 轴上的角有两个,即 90°,270°角(如图),因此,所有与90°角终边相同的角构成集合
S ={β |β=90°+k · 360°,k ∈Z},
而所有与270°角终边相同的角构成集合
S ={β |β=270°+k · 360°,k ∈Z},
于是,终边在y 轴上的角的集合
S=S US
={β |β=90°+2k · 180°,k ∈Z}U{β |β=90°+180°+2k · 180°,k ∈Z} ={β |β=90°+2k · 180°,k ∈Z}U{β |β=90°+(2k+1)180°,k ∈Z}
={β |β=90°+n · 180°,n ∈Z}.
例题讲解
4
(人教A版2019)
例3
写出终边在直线y=x 上的角的集合S.S中满足不等
式-360°≤β<720°的元素β有哪些
核心素养:数学运算
解析
如图,在直角坐标系中画出直线y=x,可以发现
它与x 轴的夹角是45°,在0°~360°范围内,终边在直线y=x 上的角有两个:45°,225°。因此,终边在直线y=x 上的角的集合
S={β |β=45°+k · 360°,k ∈Z}U{β |β=225°+k · 360°,k ∈Z}
={β |β=45°+n · 180°,n ∈Z}.
S 中适合不等式-360°≤β<720°的元素β有
45°-2×180°=—315°,
45°-1×180°=—135°,
45°+0×180°=45°,
45°+1×180°=225°,
45°+2×180°=405°,
45°+3×180°=585°.
课堂练习
5
【解析】
终边落在第一象限的角不一定是锐角,如400°的角是第一象限角,但不是锐角,故①的说法是错误的;
同理第二象限角也不一定是钝角,故③的说法也是错误的.
下列说法中,正确的是______(填序号).
①终边落在第一象限的角为锐角; ②锐角是第一象限角;
③第二象限角为钝角; ④角α与-α的终边关于x轴对称.
【训练1】
课堂练习
5
【解析】
因为-1 845°=-45°+(-5)×360°,
所以-1 845°角与-45°角的终边相同.
所以与角α终边相同的角的集合是{β|β=-45°+k·360°,k∈Z}.
(1)最小的正角为315°.
(2)最大的负角为-45°.
(3)-360°~720°之间的角分别是-45°,315°,675°.
已知α=-1 845°,在与α终边相同的角中,求满足下列条件的角.
(1)最小的正角;(2)最大的负角;(3)-360°~720°之间的角.
【训练2】
课堂练习
5
【解析】
直角不属于任何一个象限,故A不正确;
120°是第二象限角,故B正确;
由于120°是第二象限角,390°是第一象限角,120°<390°,故C不正确;
270°的终边在y轴上,它不属于任何一个象限,故D正确.
故选BD.
(多选)下列叙述正确的是( )
A.三角形的内角是第一象限角或第二象限角 B.120°是第二象限角
C.第二象限角比第一象限角大 D.270°不属于任何一个象限
【训练3】
课堂小结
6
1.总结一下本节课我们做了什么?你获得了哪些知识?
2.本节课的知识点总结.
3.你对本节课知识的理解是什么?
任意角
核心知识
方法总结
易错提醒
核心素养
角的概念、表示及分类
象限角
终边相同的角
象限角的两种判断方法:(1)化成终边相同角的表示形式;(2)在坐标系中画出相应的角,观察终边的位置
求在给定范围内终边相同角的方法:写出终边相同的角的表示,根据给定范围建立关于k的不等式,解出k,根据k确定角
终边相同的角中必须保证k是整数
数学抽象:通过具体实例抽象出象限角、终边相同角的概念,培养数学抽象的核心素养
课后作业
7
1. 思考:今天是星期三,那么7k(k∈Z)天后的那一天是星期几
7k(k∈Z)天前的那一天是星期几 100天后的那一天是星期几 ;
2. 完成课本171页 3,4,5
必做
3. 完成课本175页复习巩固1,2
选做
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
