高中数学人教A版(2019)必修2 8.5 空间直线、平面平行 解答题章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 8.5 空间直线、平面平行 解答题章节综合练习题(答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 08:43:20 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
8.5 空间直线、平面平行 解答题
一、解答题
1.四棱锥的底面为正方形,为的中点.
(1)证明:平面;
(2)若平面,证明:.
2.如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,D是AC的中点,AA1=AB=2.
(1)求证:AB1∥平面C1BD;
(2)若异面直线AC和A1B1所成角的余弦值为,求四棱锥B-AA1C1D的体积.
3.在直三棱柱中,、、、分别为,,,中点,.
(1)求证:平面.
(2)求二面角的余弦值.
4.如图,四棱锥中,ABCD为正方形,E为PC的中点,平面平面ABCD,.
(1)证明:平面BDE;
(2)求三棱锥的体积.
5.(2023高二上·西乡县开学考)如图,在三棱柱 中, 底面 ,且 为等边三角形, ,D为 的中点.
(1)求证:直线 平面 ;
(2)求证:平面 平面 ;
(3)求三棱锥 的体积.
6.如图,四棱锥中,侧面为等边三角形且垂直于底面,四边形为梯形,,.
(1)若为的中点,求证:平面;
(2)若直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
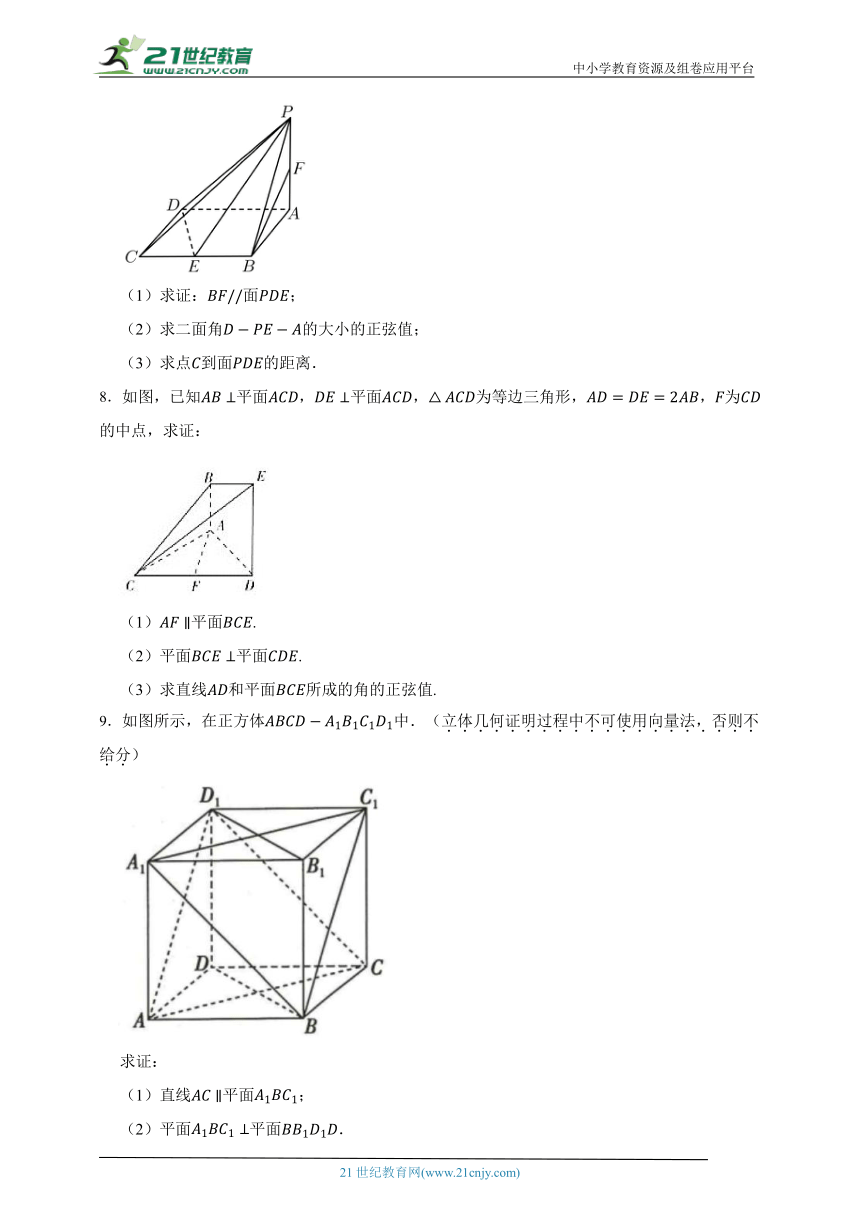
7.在四棱锥中,底面是边长为的菱形,,面,,,分别为,的中点.
(1)求证:面;
(2)求二面角的大小的正弦值;
(3)求点到面的距离.
8.如图,已知平面,平面,为等边三角形,,为的中点,求证:
(1)平面.
(2)平面平面.
(3)求直线和平面所成的角的正弦值.
9.如图所示,在正方体中.(立体几何证明过程中不可使用向量法,否则不给分)
求证:
(1)直线平面;
(2)平面平面.
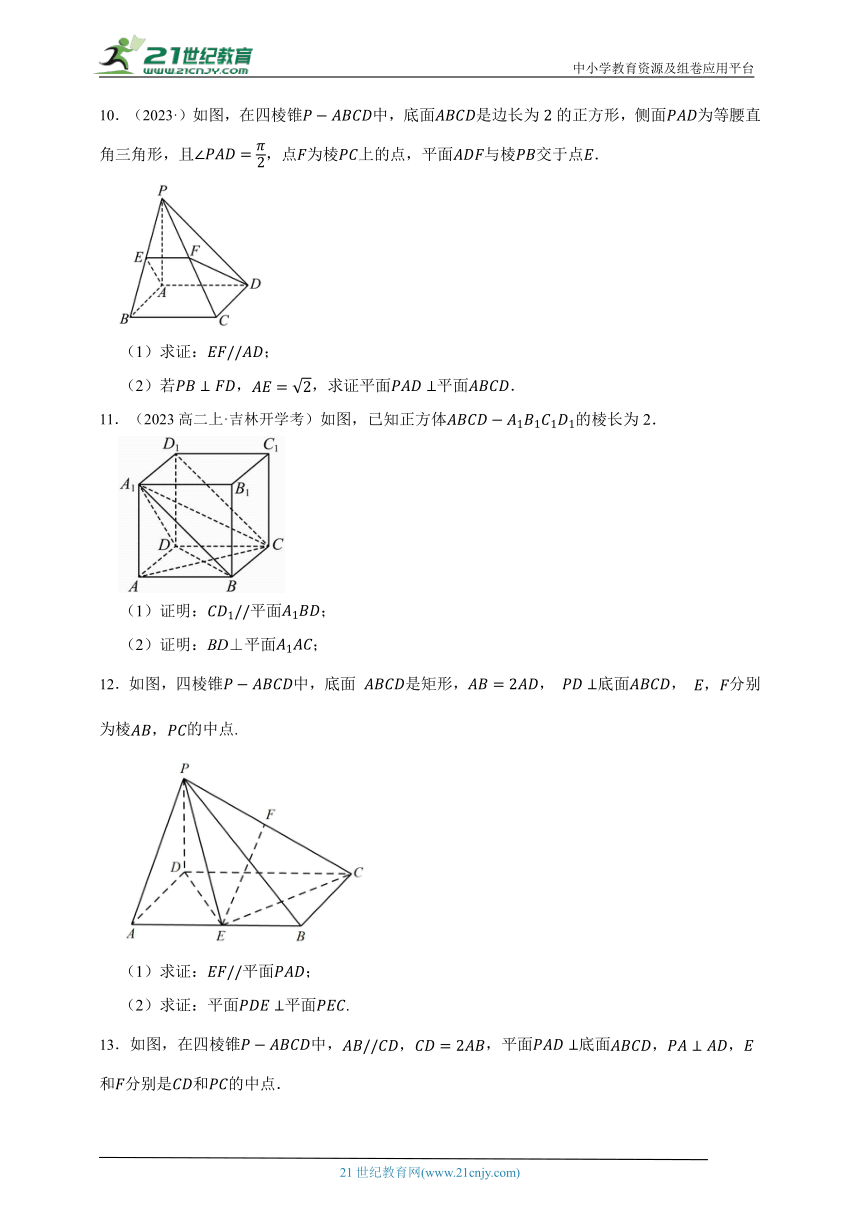
10.(2023·)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)若,,求证平面平面.
11.(2023高二上·吉林开学考)如图,已知正方体的棱长为2.
(1)证明:平面;
(2)证明:BD⊥平面;
12.如图,四棱锥中,底面 是矩形,, 底面, 分别为棱的中点.
(1)求证:平面;
(2)求证:平面平面.
13.如图,在四棱锥中,,平面底面和分别是和的中点.
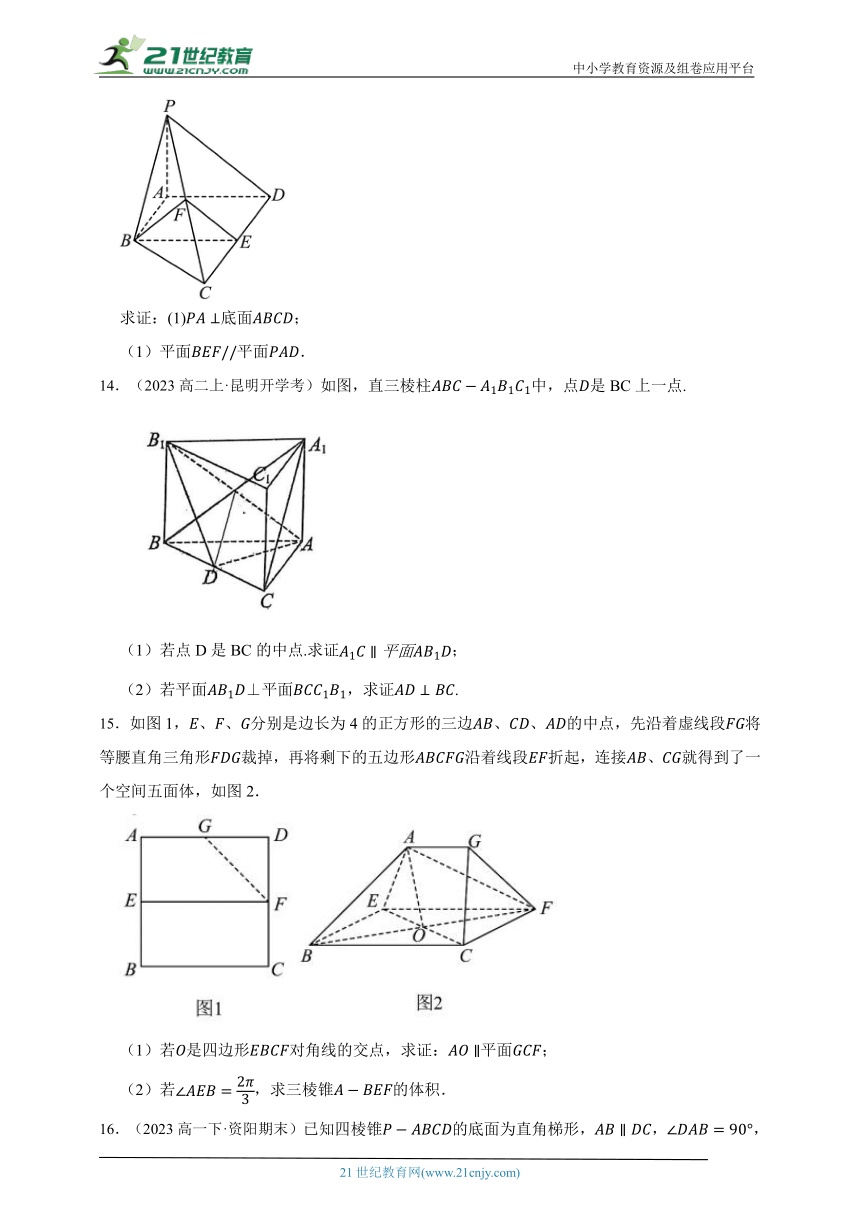
求证:(1)底面;
(1)平面平面.
14.(2023高二上·昆明开学考)如图,直三棱柱中,点是BC上一点.
(1)若点D是BC的中点.求证;
(2)若平面⊥平面,求证.
15.如图1,、、分别是边长为4的正方形的三边、、的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接、就得到了一个空间五面体,如图2.
(1)若是四边形对角线的交点,求证:平面;
(2)若,求三棱锥的体积.
16.(2023高一下·资阳期末)已知四棱锥的底面为直角梯形,,,底面ABCD,且,,M是PB的中点.
(1)证明:平面;
(2)判断直线CM与平面的位置关系,并证明你的结论;
(3)求二面角的余弦值.
17.如图,四棱锥中,底面ABCD为矩形,平面ABCD,E为PD的中点.
(1)证明://平面AEC;
(2)设三棱锥的体积是,,求平面DAE与AEC的夹角.
18.(2023高二上·西乡县开学考)如图,在正三棱柱(侧棱垂直于底面,且底面是正三角形)中,,,,分别是,,的中点.
(1)求证:平面平面;
(2)求证:平面
19.(2023高一下·上饶期末)如图,正四棱台中,,,.
(1)证明:平面;
(2)若,求异面直线与所成的角的余弦值.
20.如图,在几何体中,已知四边形是正方形,,分别为的中点,为上靠近点的四等分点.
(1)证明://平面;
(2)证明:平面//平面.
21.(2023高一下·汕尾期末)如图,在正方体中,,分别为棱,的中点,是线段上的动点.证明:
(1)平面;
(2)平面.
22.(2023高一下·安徽月考)如图,在直三棱柱中,,,D,E分别是棱,AC的中点.
(1)判断多面体是否为棱柱并说明理由;
(2)求多面体的体积;
(3)求证:平面平面AB1D.
23.(2023高一下·衢州期末) 衢州市某公园供市民休息的石凳是阿基米德多面体,它可以看做是一个正方体截去八个一样的四面体得到的二十四等边体(各棱长都相等),已知正方体的棱长为30cm.
(1)证明:平面平面;
(2)求石凳所对应几何体的体积.
24.(2023高一下·浙江月考)在三棱锥中,底面是边长为2的正三角形,底面是的中点,是的中点,分别在线段和上,且.
(1)证明:平面平面.
(2)求直线与底面所成角的大小.
25.(2023·上海市模拟) 如图,矩形AMND所在平面与直角梯形MBCN所在的平面垂直,MB//NC,MN⊥MB.
(1)求证:平面AMB//平面DNC;
(2)若MC⊥CB,求证:BC⊥AC.
26.(2023高一下·浙江期中) 如图,在正方体中,分别是棱的中点,设是线段上一动点.
(1)证明://平面;
(2)求三棱锥的体积.
27.(2023·嵊州模拟)如图,在直四棱柱中,在棱上,满足在棱上,满足.
(1)当时,证明:平面;
(2)若平面与平面所成的锐二面角的余弦值为,求的值.
28.(2023高二上·朝阳开学考)如图,四边形ABCD是矩形,平面ABCD,平面ABCD,,,点F在棱PA上.
(1)求证:平面CDE;
(2)求二面角的余弦值;
(3)若点F到平面PCE的距离为,求线段AF的长.
29.(2023高二上·柳州开学考)如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠ABC=60°,AA1⊥平面ABCD,E为AA1中点,AA1=AB=2.
(1)求证:AC1∥平面B1D1E;
(2)求三棱锥A﹣B1D1E的体积;
(3)在AC1上是否存在点M,满足AC1⊥平面MB1D1?若存在,求出AM的长;若不存在,说明理由.
30.(2022高一下·电白期末)如图所示,矩形中,,.、分别在线段和上,,将矩形沿折起.记折起后的矩形为,且平面平面.
(1)求证:平面;
(2)若,求证:;
(3)求四面体体积的最大值
答案解析部分
1.【答案】(1)证明:设与交于点,连接,因为底面是正方形,所以为的中点,又因为为的中点,所以,因为平面平面,所以平面
(2)解:因为底面是正方形,所以,
又因为平面平面,所以,
又平面,所以平面,
因为平面,所以
【解析】【分析】 (1)设与交于点,连接,利用中位线证明,进而证明平面;
(2) 通过证明,,得到平面,所以 .
2.【答案】(1)在直三梭柱中,侧面四边形是平行四边形,
交于,连接DO,
则是的中点,又是AC的中点,
所以平面平面,
所以平面;
(2)过作于,因为平面平面ABC,
所以,
又平面,所以平面.
异面直线AC和所成角的余弦值为,
即直线AC和AB所成角的余弦值为.
在Rt中,,
所以
,
,
四棱锥的体积
.
【解析】
【分析】(1) 交于,连接DO, 利用中位线定理证明AB1∥平面C1BD;
(2) 过作于 ,利用几何法求出异面直线和所成角的余弦值为 ,求出梯形的面积,代入四棱锥的体积公式,计算求解即可.
3.【答案】(1)解:证明:取中点,连接,,易知,,
,分别是,的中点,,
,,四边形为平行四边形,,
不在平面内,在平面内,平面.
(2)解:取的中点,连接,,以为坐标原点
,,分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,故,
设平面的一个法向量为,
则,则可取,
易知平面的一个法向量为,
,二面角的余弦值为.
【解析】【分析】本题考查线面平行的判定与二面角的余弦值。
(1)找中点利用中位线得出,即 四边形为平行四边形,, 所以;
(2)建立空间直角坐标系,求出平面FA1C1的法向量,再利用向量夹角的余弦值公式即得解。
4.【答案】(1)证明:连接AC交BD于点O,连接OE,
因为四边形ABCD为正方形,所以点O为AC的中点,
又E为PC的中点,所以,
又因为平面BDE,平面BDE,所以平面BDE.
(2)解:∵四边形ABCD为正方形,则,
因为,
所以.
【解析】【分析】 (1)连接AC交BD于点O,连接OE, 可得 , 结合线面平行的判定定理分析证明;
(2)利用转换顶点法结合锥体的体积公式运算求解.
5.【答案】(1)连接 交 于 ,连接 ,在 中, 为 中点, 为 中点,所以 ,又 面 ,∴直线 面 ;
(2)∵ 面 , 面 ,∴ .又 ,
,∴ , 面 ,∴ 面 .
又 面 ,∴面 面 ;
(3)∵ 为正三角形, 为 中点,∴ ,由 ,可知 ,
.∴ ,又∵ 面 ,且 ,
∴ 面 ,且 ,∴ .
【解析】【分析】(1)根据直线与平面平行的判定定理求解即可;
(2)根据直线与平面垂直性质定理及判定定理,结合平面与平面垂直的判定定理求解即可;
(3)运用等体积法,结合棱锥的体积公式求解即可.
6.【答案】(1)解:取中点,连接,
分别为中点,,,
,,又,
,,四边形为平行四边形,,
平面,平面,平面.
(2)解:取中点,连接,
,,四边形为平行四边形,
又,,即;
为等边三角形,,
又平面平面,平面平面,平面,
平面;
则以为坐标原点,正方向为轴,可建立如图所示空间直角坐标系,
设,,则,,,,,
,,,,
设平面的法向量,
则,令,解得:,,,
,解得:,;
设平面的法向量,
则,令,解得:,,;
,
即平面与平面所成锐二面角的余弦值为.
【解析】【分析】 (1) 根据平行的性质可得 ,结合线面平行的判定定理分析证明;
(2)根据面面垂直的性质定理可得平面 ,以为坐标原点,正方向为轴,可建立示空间直角坐标系,利用空间向量求面面夹角.
7.【答案】(1)证明:如图所示,取中点,连结,
因为分别为的中点,所以可证得,且,
所以四边形是平行四边形,所以,又因为平面,平面,
所以平面
(2)解:作于点,作于点,连结,易证平面,
所以,又因为,,
所以平面,所以,所以即为二面角的平面角,
在中,
(3)解:因为,所以
所以
【解析】【分析】(1)取中点,连结,先证明四边形是平行四边形得到,再利用线面平行的判定定理可得证明;
(2)作于点,作于点,连结,利用定义可得到即为二面角的平面角,在中解三角形即可;
(3)先求出与,再利用等体积法即可求得点到面的距离.
8.【答案】(1)证明:
(2)证明:
(3)解:
【解析】
(1)取CE中点M,连结MF,BM,
MF是△CDE的中位线,∴MF∥DE,,
∵AB⊥平面ACD,DE⊥平面ACD,
∴DE∥AB,又DE=2AB,∴AB∥MF,AB=MF,
∴四边形ABMF是平行四边形,
∴AF∥BM,∵AF 平面BCE,BM 平面BCE,
∴AF//平面BCE;
(2)∵AB⊥平面ACD,AF 平面ACD,
∴AB⊥AF,∴四边形ABMF是矩形,∴BM⊥MF.
∵△ACD是正三角形,F是CD中点,∴CD⊥AF.
∵BM∥AF,∴CD⊥BM,
∵MF∩CD=F,MF 平面CDE,CD 平面CDE,
∴BM⊥平面CDE,∵BM 平面BCE,
∴平面BCE⊥平面CDE;
(3)取线段DE的中点P,连接BP,
∵AB∥DP且AB=DP,
∴四边形ABPD是平行四边形,
∴AD∥BP,
则直线AD和平面BCE所成的角就是直线BP和平面BCE所成的角,
过点P作PN⊥CE,垂足为N,连结BN,
由(2)知平面BCE⊥平面CDE,又平面BCE∩平面CDE=CE,
∴PN⊥平面BCE,∴∠PBN为直线BP和平面BCE所成角的平面角.
设AB=1,则DE=AC=CD=AD=2,
∵DE⊥平面ACD,
∴DE⊥DC,
∵CD=DE,
∴,
∵PN⊥CE,EP=1,
∴,
∵四边形ABPD为平行四边形,
∴BP=AD=2,
∴,
故直线AD和平面BCE所成的角正弦值为.
【分析】(1)根据题意可得AF∥BM,结合线面平行的判定定理分析证明;
(2)根据题意题意可证BM⊥平面CDE,结合面面垂直的判定定理分析证明;
(3)根据(2)可知PN⊥平面BCE,则∠PBN为直线BP和平面BCE所成角的平面角,分析运算即可.
9.【答案】(1)证明:在正方体中,
因为平面平面,
平面
(2)证明:在正方体中,
易知平面中,又因为平面,
所以,
又因为平面,
所以平面,
又因为平面,
所以平面平面.
【解析】【分析】 (1) 根据题意可得 ,进而结合线面平行的判定定理分析证明;
(2)根据题意可证 平面, 进而结合面面垂直的判定定理分析证明.
10.【答案】(1)证明:因为底面是正方形,所以,
平面,平面,所以平面,
又因为平面与交于点,平面,平面平面,
所以.
(2)证明:侧面为等腰直角三角形,且,即,,
因为,,且两直线在平面内,可得平面,
因为平面,则.
又因为,,且两直线在平面内,
则平面,
因为平面,则,
因为,所以为等腰三角形,所以点为的中点.
又因为,所以为等腰直角三角形,
因为,所以AP⊥面,
因为面APD,所以面APD⊥面.
【解析】【分析】(1)根据线面平行可得 平面, 再结合线面平行的性质定理分析证明;
(2)根据题意可证 平面, 可得 ,同理可证 ,进而可得AP⊥面, 结合面面垂直的判定定理分析证明.
11.【答案】(1)解:在正方体,且,
∴为平行四边形,∴,∵平面,平面
∴平面;
(2)解:∵正方体,底面ABCD,底面ABCD,∴,
∵正方形ABCD中,,又∵平面,平面,,
∴平面;
【解析】【分析】(1)根据正方体的性质可得 , 进而结合线面平行的判定定理分析证明;
(2)根据正方体的性质可得 ,, 进而结合线面垂直的判定定理分析证明
12.【答案】(1)证明:取的中点,连接,
因为分别是的中点,
所以,且,
又是的中点,所以,且,
所以,且,
所以是平行四边形,故.
又平面,平面,
所以平面.
(2)因为底面,底面,
所以.
取中点,连接,
因为是矩形,且,
所以都是正方形,
所以,即.
又是平面内的两条相交直线,
所以平面.
而平面,所以平面平面.
【解析】【分析】 (1)取的中点,连接, 根据平行性质可得 ,结合线面平行的性质定理分析证明;
(2) 根据题意先证 平面,再结合面面垂直的判定定理分析证明.
13.【答案】(1)∵和分别是和的中点,
∴,
而平面平面,
∴平面.
∵,
∴四边形是平行四边形.
∴,而平面平面,
∴平面.
而平面平面,
∴平面平面.
【解析】(1)因为 , 平面底面,平面底面,平面,
所以 底面.
【分析】(1)根据题意利用面面垂直的性质定理分析证明;
(2)根据题意可证 , ,结合面面平行的判定定理分析证明.
14.【答案】(1)连接 交于点,连接 ,则是中点,又 D是的中点 ,,又, , ;
(2)过点作,又平面⊥平面 ,平面平面,平面,平面,
平面,,
由直三棱柱性质知平面,又平面,,
又平面 ,平面 ,,平面,
平面, .
【解析】【分析】 (1) 、连接 交于点,连接 ,通过证明得到 ;
(2) 、过点作,通过证明和得到平面,进而证明.
15.【答案】(1)在图2中取线段中点,连接、,如图所示:
由图1可知,四边形是矩形,且,
∴是线段与的中点,∴且,
图1中且,而且.
所以在图2中,且,
∴且,
∴四边形是平行四边形,则,
由于平面,平面,
∴平面.
(2)∵,,,面,,∴平面,
,
所以,
即三棱锥的体积为.
【解析】【分析】(1)取线段中点,连接、,通过证明四边形是平行四边形得到,再结合线面平行的判定定理可得证明;
(2)由已知可证明平面,再利用等体积法,即,先求出,再利用锥体体积公式计算即可.
16.【答案】(1)证明:由底面ABCD,底面ABCD,则,
在直角梯形中,,则,
又,平面,所以平面;
(2)解:平面,证明如下:
如图:
取PA中点E,连接ME,DE,由于M是PB的中点,故,且,
由,则,且,
从而四边形是平行四边形,故,
又平面,平面,所以平面;
(3)解:作,垂足为N,连接BN,如图:
在中,,又,所以≌,可得,
则≌,故,故为所求二面角的平面角,
由(1)知平面,由平面,可得,
在中,,所以,
在等腰三角形中,,所以,
因为,在中,由余弦定理得,
所以二面角的余弦值为.
【解析】【分析】(1)由底面ABCD,推出,再由为直角梯形,推出,结合线面垂直的性质及判定定理即可证明;
(2) 取中点E,连接ME,DE, 根据已知条件,再利用线面平行的判定定理即可证明;
(3) 作,垂足为N,连接BN, 易知,,确定为二面角的平面角,由(1)推出,在和等腰三角形中求出以及得长度,最后利用余弦定理求二面角的余弦值即可.
17.【答案】(1)证明:以点A为坐标原点,建立如图所示的空间直角坐标系,设,
由几何关系有:,
则直线的方向向量为:,,
设平面的法向量,则:,
据此可得:平面的一个法向量为,
结合可知:,即
据此可得:平面.
(2)解:因为平面ABCD,E为PD的中点.,
所以点E到平面ABCD的距离为,
因为三棱锥的体积是,
所以有,
结合(1)的结论可知:,
则平面的一个法向量为.
由平面可知平面的一个法向量为:,
据此可得:,
则,
观察可知二面角的平面角为锐角,
故二面角的余弦值为.
【解析】【分析】(1)以点A为坐标原点, 建立空间直角坐标系,设,,求出平面的法向量, 利用空间向量数量积计算得,所以平面 ;
(2) 由三棱锥的体积是,推出,由题意得出平面的一个法向量为 , 平面的一个法向量为, 根据空间向量夹角公式,计算求解即可.
18.【答案】(1)证明:如图,
因为N,P分别是AB,的中点,
所以,
又 平面, 平面,
所以 平面,
又M是的中点,
所以,
所以四边形是平行四边形,
所以,
又 平面, 平面,
所以 平面,
因为,
所以平面平面;
(2)解:连接,交于T,连接MT,
因为 ,底面是等边三角形,
所以四边形是正方形,
所以,且T为的中点,
又,
所以,
因为,平面,所以 平面 .
【解析】【分析】(1)分别证明平面,平面,利用面面平行的判定定理证明即可;
(2)连接,交于T,连接MT,分别证明,,结合线面垂直的判定定理可得证明.
19.【答案】(1)解:∵正四棱台中,,,
∴,又∵,
∴,∴四边形为平行四边形,
∴,又∵平面,平面,
∴平面,
∵,平面,平面,∴平面,
又∵,平面,平面,
∴平面平面,
∵平面,∴平面.
(2)解:在等腰梯形中作交于点,
由(1)知,,∴,
∴就是异面直线与所成的角,
∵,,
∴中,,,
∴,
∴异面直线与所成的角的余弦值为.
【解析】【分析】(1)根据面面平行的判定定理可得 平面平面, 结合面面平行的性质可得 平面.
(2)根据题意可知 就是异面直线与所成的角, 结合余弦定理运算求解.
20.【答案】(1)证明:如图,连接,设与相交于点,连接,
因为四边形是正方形,则为的中点,又为的中点,
于是,,即四边形为平行四边形,则,
而平面,平面,
所以平面.
(2)解:取的中点,连接,因为,且,
则四边形都为平行边形,有,
于是四边形为平行四边形,即有,
而为上靠近点的四等分点,则为的中点,又为的中点,则,
因此,又平面,平面,则平面,
显然,又平面,平面,则平面,
而平面,
所以平面平面.
【解析】【分析】(1)先证明,再利用线面平行的判定定理即可得证;
(2)先证明平面和平面,利用面面平行的判定定理即可得证.
21.【答案】(1)证明:如图,连接交于点,连接.
∵为的中点,为的中点,
∴为的中位线,
∴.
又∵平面,平面,
∴平面
(2)证明:连接,,连接交于点,连接,如图.
在正方体中,,
∵平面,平面,
∴平面.
又为的中位线,
∴.
∵平面,平面,
∴平面.
又∵平面,平面,,
∴平面平面.
∵平面,
∴平面.
【解析】【分析】 (1) 根据题意可得,进而结合线面平行的判定定理分析证明;
(2) 根据题意可得平面,平面,进而可得平面平面,结合面面平行的性质定理分析证明.
22.【答案】(1)解:多面体不是棱柱.理由如下:
因为棱柱的侧面必为平行四边形,故棱柱的面至少有3个平行四边形,而多面体只有1个面是平行四边形,故不是棱柱.
(2)解:易知三棱柱的体积,
三棱锥的体积,
易知三棱锥的体积等于三棱锥的体积,
故多面体的体积.
(3)解:因为D,E分别是,AC的中点,所以,
所以四边形为平行四边形
所以.又平面,平面,所以平面.
易知,得四边形为平行四边形.
所以,又平面,平面,所以平面.
而,BE,平面,
所以平面平面.
【解析】【分析】(1)利用已知条件和棱柱的概念判断即可;
(2)利用间接法求多面体的体积,即;
(3)利用已知条件可证得四边形BB1DE和四边形ADC1E都是平行四边形,进而得到 , ,利用线面平行的判定定理可得: 平面 , 平面 ,再利用面面平行的判定定理即可得证.
23.【答案】(1)解:多面体为二十四等边体知、、、、、为正方体对应棱上的中点
则,,
,平面,,平面,
则平面平面.
(2)解:正方体的体积,
截去的每个四面体体积为,
所以石凳所对应几何体的体积为.
【解析】【分析】(1)由面面平行的判定定理即可证明.
(2)先求出八个全等的三棱锥的体积和,再利用正方体的体积减去截去的部分体积即可算出.
24.【答案】(1)证明:取的中点,取上靠近的四等分点,连接,
,
且,
,
且,
且,
四边形是平行四边形,
,又平面,平面,
平面,
,
,
又平面平面,
平面,
平面
平面平面.
(2)解:由(1)知,又底面,
底面,连接,
就是与底面所成的角.
在中,,
,
,
与底面所成角的大小是.
【解析】【分析】 (1)根据比例关系可得线线平行,由此可得线面平行,再由面面平行的判定定理得证平面平面.
(2)根据线面角的定义得出就是与底面所成的角.再求解即可得直线与底面所成角的大小.
25.【答案】(1)证明:因为MB//NC,MB 面DNC,NC 面DNC,
所以MB//面DNC.因为AMND是矩形,所以MA//DN,又MA 面DNC,
DN 面DNC,所以MA//面DNC.又MA∩MB=M,且MA、MB 平面AMB,所以面AMB//面DNC.
(2)证明:因为AMND是矩形,所以AM⊥MN.
因为面AMND⊥面MBCN,且面AMND∩面MBCN=MN,AM 面AMND,
所以AM⊥平面MBCN,而BC 平面MBCN,所以AM⊥BC.
因为MC⊥BC,MC∩AM=M,MC、AM 面AMC,所以BC⊥面AMC,
因为AC 面AMC,所以BC⊥AC.
【解析】【分析】(1)由线面平行的判定可证MB//面DNC、MA//面DNC,再用面面平行的判定证结论;
(2)由面面垂直的性质得AM⊥平面MBCN,再由线面垂直的性质、判定证BC⊥面AMC,最后由线面垂直的性质证线线垂直即可.
26.【答案】(1)证明:连结,,
因为正方体,所以,且,
所以四边形为平行四边形,
所以,平面,平面,
所以平面,
取中点,连结,
因为是和的中点,
所以,,
且,,
所以,且,
所以四边形为平行四边形,
所以,且,
因为,且,
所以四边形为平行四边形,
所以,且,
所以,平面,平面,
所以平面,,平面,平面,
所以平面平面,平面,所以平面,
(2)解:因为正方体,
所以点到平面的距离与点到平面的距离相等,
所以三棱锥的高,
所以
【解析】【分析】
(1)可以通过证明面面平行进而得到线面平行
(2)根据正方体的的体积特点,得出体积之间的数量关系,从而得出高和几何体的体积.
27.【答案】(1)证明:
方法1:
在棱上取,使得,连接.
因为,所以,且.
当时,,则,且,
所以,
所以四边形是平行四边形,所以.
又因为平面平面,
所以平面.
方法2:
在棱上取,使得,连接.
因为,所以
又平面,平面,所以平面.
又因为,且,所以四边形是平行四边形,
所以,又平面,平面,从而平面.
因为平面,所以平面平面,
因为平面
所以平面.
(2)解:取的中点,则.分别以射线为轴的正半轴建立空间直角坐标系,如图所示,
则,所以.
因为,所以,所以.
设是平面的法向量,
则,可取.
不难得到:平面的一个法向量为.
所以,化简得:,
解得,或.因为,所以.
【解析】【分析】 (1) 方法一:在棱上取,使得,连接,根据平行的性质可证,进而可得结果;方法二:在棱上取,使得,连接,先证平面平面,根据面面平行的性质可得结果;
(2) 分别以射线为轴的正半轴建立空间直角坐标系,求平面的法向量,根据面面夹角的向量求法可得结果.
28.【答案】(1)证明:在矩形ABCD中,.
因为平面CDE,平面CDE,
所以平面CDE.
因为平面ABCD,平面ABCD,
所以.
因为平面CDE,平面CDE,
所以平面CDE.
又因为平面PAB,平面PAB,.
所以平面平面CDE.
因为平面PAB,
所以平面CDE.
(2)解:因为平面ABCD,平面ABCD,平面ABCD,
所以,.
又因为ABCD是矩形,,
所以AD,AB,PA两两垂直,如图建立空间直角坐标系,
则,,,
所以,.
设平面PEC的一个法向量为,则
,即.
令,则,.
于是.
取平面PEA的法向量为.
则.
由图可知二面角为锐角,
所以二面角的余弦值是.
(3)解:令线段AF的长为t,则,.
所以,
因为点F到平面PCE的距离.
所以,即.
解得或(舍).
所以线段AF的长为.
【解析】【分析】(1) 通过证明平面平面 ,从而证明 平面;
(2) 先证明,,两两垂直,建立空间直角坐标系,利用空间向量求二面角的余弦值;
(3)设线段的长为,则,利用点到平面距离公式列方程,求出即可.
29.【答案】(1)证明:连A1C1交B1D1于点F,连EF,
∵A1B1C1D1是菱形,∴F是A1C1中点,∵E是AA1中点,∴EF∥AC1,
∵EF 平面B1D1E,AC1 平面B1D1E,∴AC1∥平面B1D1E.
(2)解:过B1作B1H⊥D1A1的延长线于点H,
由AA1⊥底面ABCD知AA1⊥平面A1B1C1D1,则AA1⊥B1H,又AA1∩1A1=A1,B1H⊥平面AA1D1D.
由∠A1B1C1=∠ABC=60°知∠B1A1H=60°,
又A1B1=2,则.
(3)解:∵AA1⊥平面ABCD,平面A1B1C1D1∥平面ABCD,
∴AA1⊥平面A1B1C1D1,∵B1D1 平面A1B1C1D1,∴B1D1⊥AA1,
∵菱形A1B1C1D1中B1D1⊥A1C1,A1C1∩AA1=A1,A1C1,AA1 平面AA1C1,
∴B1D1⊥平面AA1C1,又AC1 平面AA1C1,∴AC1⊥B1D1,
过F在Rt△AA1C1中,作FM⊥AC1,垂足为M,
则由FM∩B1D1=F,FM,B1D1 平面MB1D1知AC1⊥平面MB1D1,
∴存在M满足条件,在Rt△AA1C1中,AA1=A1C1=2,,F是A1C1中点,
∴,∴.
【解析】【分析】(1)连A1C1交B1D1于点F,连EF,通过中位线证明EF∥AC1,得到AC1∥平面B1D1E;
(2)过B1作B1H⊥D1A1的延长线于点H,得到B1H⊥平面AA1D1D,所以 ,进而求解;
(3)由AA1⊥平面ABCD和菱形A1B1C1D1得到B1D1⊥平面AA1C1,所以AC1⊥B1D1,则过F作FM⊥AC1,垂足为M,有AC1⊥平面MB1D1,再求解.
30.【答案】(1)证明:∵四边形,都是矩形,
∴,,∴四边形是平行四边形,
∴,∵平面,∴平面;
(2)证明:连接,设,∵平面平面,且,
∴平面,∴,
又,∴四边形为正方形,∴,
∴平面,又平面,∴,
(3)解:设,则,其中,
由(1)得平面,
∴四面体的体积为:
,
时,四面体的体积最大,其最大值为2.
【解析】【分析】(1) 连接,设,利用平面平面,且结合面面垂直的性质对立证出线面垂直,所以平面,再利用线面垂直的定义证出线线垂直,所以,再利用,所以四边形为正方形,所以,再利用线线垂直证出线面垂直,所以平面,再利用线面垂直的定义证出线线垂直,从而证出。
(2) 设,则,其中,由(1)得平面,再利用三棱锥的体积公式和二次函数的图象求最值的方法得出四面体的体积的最大值。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
8.5 空间直线、平面平行 解答题
一、解答题
1.四棱锥的底面为正方形,为的中点.
(1)证明:平面;
(2)若平面,证明:.
2.如图,在直三棱柱ABC-A1B1C1中,AB⊥BC,D是AC的中点,AA1=AB=2.
(1)求证:AB1∥平面C1BD;
(2)若异面直线AC和A1B1所成角的余弦值为,求四棱锥B-AA1C1D的体积.
3.在直三棱柱中,、、、分别为,,,中点,.
(1)求证:平面.
(2)求二面角的余弦值.
4.如图,四棱锥中,ABCD为正方形,E为PC的中点,平面平面ABCD,.
(1)证明:平面BDE;
(2)求三棱锥的体积.
5.(2023高二上·西乡县开学考)如图,在三棱柱 中, 底面 ,且 为等边三角形, ,D为 的中点.
(1)求证:直线 平面 ;
(2)求证:平面 平面 ;
(3)求三棱锥 的体积.
6.如图,四棱锥中,侧面为等边三角形且垂直于底面,四边形为梯形,,.
(1)若为的中点,求证:平面;
(2)若直线与平面所成角的正弦值为,求平面与平面所成锐二面角的余弦值.
7.在四棱锥中,底面是边长为的菱形,,面,,,分别为,的中点.
(1)求证:面;
(2)求二面角的大小的正弦值;
(3)求点到面的距离.
8.如图,已知平面,平面,为等边三角形,,为的中点,求证:
(1)平面.
(2)平面平面.
(3)求直线和平面所成的角的正弦值.
9.如图所示,在正方体中.(立体几何证明过程中不可使用向量法,否则不给分)
求证:
(1)直线平面;
(2)平面平面.
10.(2023·)如图,在四棱锥中,底面是边长为的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.
(1)求证:;
(2)若,,求证平面平面.
11.(2023高二上·吉林开学考)如图,已知正方体的棱长为2.
(1)证明:平面;
(2)证明:BD⊥平面;
12.如图,四棱锥中,底面 是矩形,, 底面, 分别为棱的中点.
(1)求证:平面;
(2)求证:平面平面.
13.如图,在四棱锥中,,平面底面和分别是和的中点.
求证:(1)底面;
(1)平面平面.
14.(2023高二上·昆明开学考)如图,直三棱柱中,点是BC上一点.
(1)若点D是BC的中点.求证;
(2)若平面⊥平面,求证.
15.如图1,、、分别是边长为4的正方形的三边、、的中点,先沿着虚线段将等腰直角三角形裁掉,再将剩下的五边形沿着线段折起,连接、就得到了一个空间五面体,如图2.
(1)若是四边形对角线的交点,求证:平面;
(2)若,求三棱锥的体积.
16.(2023高一下·资阳期末)已知四棱锥的底面为直角梯形,,,底面ABCD,且,,M是PB的中点.
(1)证明:平面;
(2)判断直线CM与平面的位置关系,并证明你的结论;
(3)求二面角的余弦值.
17.如图,四棱锥中,底面ABCD为矩形,平面ABCD,E为PD的中点.
(1)证明://平面AEC;
(2)设三棱锥的体积是,,求平面DAE与AEC的夹角.
18.(2023高二上·西乡县开学考)如图,在正三棱柱(侧棱垂直于底面,且底面是正三角形)中,,,,分别是,,的中点.
(1)求证:平面平面;
(2)求证:平面
19.(2023高一下·上饶期末)如图,正四棱台中,,,.
(1)证明:平面;
(2)若,求异面直线与所成的角的余弦值.
20.如图,在几何体中,已知四边形是正方形,,分别为的中点,为上靠近点的四等分点.
(1)证明://平面;
(2)证明:平面//平面.
21.(2023高一下·汕尾期末)如图,在正方体中,,分别为棱,的中点,是线段上的动点.证明:
(1)平面;
(2)平面.
22.(2023高一下·安徽月考)如图,在直三棱柱中,,,D,E分别是棱,AC的中点.
(1)判断多面体是否为棱柱并说明理由;
(2)求多面体的体积;
(3)求证:平面平面AB1D.
23.(2023高一下·衢州期末) 衢州市某公园供市民休息的石凳是阿基米德多面体,它可以看做是一个正方体截去八个一样的四面体得到的二十四等边体(各棱长都相等),已知正方体的棱长为30cm.
(1)证明:平面平面;
(2)求石凳所对应几何体的体积.
24.(2023高一下·浙江月考)在三棱锥中,底面是边长为2的正三角形,底面是的中点,是的中点,分别在线段和上,且.
(1)证明:平面平面.
(2)求直线与底面所成角的大小.
25.(2023·上海市模拟) 如图,矩形AMND所在平面与直角梯形MBCN所在的平面垂直,MB//NC,MN⊥MB.
(1)求证:平面AMB//平面DNC;
(2)若MC⊥CB,求证:BC⊥AC.
26.(2023高一下·浙江期中) 如图,在正方体中,分别是棱的中点,设是线段上一动点.
(1)证明://平面;
(2)求三棱锥的体积.
27.(2023·嵊州模拟)如图,在直四棱柱中,在棱上,满足在棱上,满足.
(1)当时,证明:平面;
(2)若平面与平面所成的锐二面角的余弦值为,求的值.
28.(2023高二上·朝阳开学考)如图,四边形ABCD是矩形,平面ABCD,平面ABCD,,,点F在棱PA上.
(1)求证:平面CDE;
(2)求二面角的余弦值;
(3)若点F到平面PCE的距离为,求线段AF的长.
29.(2023高二上·柳州开学考)如图,四棱柱ABCD﹣A1B1C1D1中,底面ABCD是菱形,∠ABC=60°,AA1⊥平面ABCD,E为AA1中点,AA1=AB=2.
(1)求证:AC1∥平面B1D1E;
(2)求三棱锥A﹣B1D1E的体积;
(3)在AC1上是否存在点M,满足AC1⊥平面MB1D1?若存在,求出AM的长;若不存在,说明理由.
30.(2022高一下·电白期末)如图所示,矩形中,,.、分别在线段和上,,将矩形沿折起.记折起后的矩形为,且平面平面.
(1)求证:平面;
(2)若,求证:;
(3)求四面体体积的最大值
答案解析部分
1.【答案】(1)证明:设与交于点,连接,因为底面是正方形,所以为的中点,又因为为的中点,所以,因为平面平面,所以平面
(2)解:因为底面是正方形,所以,
又因为平面平面,所以,
又平面,所以平面,
因为平面,所以
【解析】【分析】 (1)设与交于点,连接,利用中位线证明,进而证明平面;
(2) 通过证明,,得到平面,所以 .
2.【答案】(1)在直三梭柱中,侧面四边形是平行四边形,
交于,连接DO,
则是的中点,又是AC的中点,
所以平面平面,
所以平面;
(2)过作于,因为平面平面ABC,
所以,
又平面,所以平面.
异面直线AC和所成角的余弦值为,
即直线AC和AB所成角的余弦值为.
在Rt中,,
所以
,
,
四棱锥的体积
.
【解析】
【分析】(1) 交于,连接DO, 利用中位线定理证明AB1∥平面C1BD;
(2) 过作于 ,利用几何法求出异面直线和所成角的余弦值为 ,求出梯形的面积,代入四棱锥的体积公式,计算求解即可.
3.【答案】(1)解:证明:取中点,连接,,易知,,
,分别是,的中点,,
,,四边形为平行四边形,,
不在平面内,在平面内,平面.
(2)解:取的中点,连接,,以为坐标原点
,,分别为轴,轴,轴建立如图所示的空间直角坐标系,
则,故,
设平面的一个法向量为,
则,则可取,
易知平面的一个法向量为,
,二面角的余弦值为.
【解析】【分析】本题考查线面平行的判定与二面角的余弦值。
(1)找中点利用中位线得出,即 四边形为平行四边形,, 所以;
(2)建立空间直角坐标系,求出平面FA1C1的法向量,再利用向量夹角的余弦值公式即得解。
4.【答案】(1)证明:连接AC交BD于点O,连接OE,
因为四边形ABCD为正方形,所以点O为AC的中点,
又E为PC的中点,所以,
又因为平面BDE,平面BDE,所以平面BDE.
(2)解:∵四边形ABCD为正方形,则,
因为,
所以.
【解析】【分析】 (1)连接AC交BD于点O,连接OE, 可得 , 结合线面平行的判定定理分析证明;
(2)利用转换顶点法结合锥体的体积公式运算求解.
5.【答案】(1)连接 交 于 ,连接 ,在 中, 为 中点, 为 中点,所以 ,又 面 ,∴直线 面 ;
(2)∵ 面 , 面 ,∴ .又 ,
,∴ , 面 ,∴ 面 .
又 面 ,∴面 面 ;
(3)∵ 为正三角形, 为 中点,∴ ,由 ,可知 ,
.∴ ,又∵ 面 ,且 ,
∴ 面 ,且 ,∴ .
【解析】【分析】(1)根据直线与平面平行的判定定理求解即可;
(2)根据直线与平面垂直性质定理及判定定理,结合平面与平面垂直的判定定理求解即可;
(3)运用等体积法,结合棱锥的体积公式求解即可.
6.【答案】(1)解:取中点,连接,
分别为中点,,,
,,又,
,,四边形为平行四边形,,
平面,平面,平面.
(2)解:取中点,连接,
,,四边形为平行四边形,
又,,即;
为等边三角形,,
又平面平面,平面平面,平面,
平面;
则以为坐标原点,正方向为轴,可建立如图所示空间直角坐标系,
设,,则,,,,,
,,,,
设平面的法向量,
则,令,解得:,,,
,解得:,;
设平面的法向量,
则,令,解得:,,;
,
即平面与平面所成锐二面角的余弦值为.
【解析】【分析】 (1) 根据平行的性质可得 ,结合线面平行的判定定理分析证明;
(2)根据面面垂直的性质定理可得平面 ,以为坐标原点,正方向为轴,可建立示空间直角坐标系,利用空间向量求面面夹角.
7.【答案】(1)证明:如图所示,取中点,连结,
因为分别为的中点,所以可证得,且,
所以四边形是平行四边形,所以,又因为平面,平面,
所以平面
(2)解:作于点,作于点,连结,易证平面,
所以,又因为,,
所以平面,所以,所以即为二面角的平面角,
在中,
(3)解:因为,所以
所以
【解析】【分析】(1)取中点,连结,先证明四边形是平行四边形得到,再利用线面平行的判定定理可得证明;
(2)作于点,作于点,连结,利用定义可得到即为二面角的平面角,在中解三角形即可;
(3)先求出与,再利用等体积法即可求得点到面的距离.
8.【答案】(1)证明:
(2)证明:
(3)解:
【解析】
(1)取CE中点M,连结MF,BM,
MF是△CDE的中位线,∴MF∥DE,,
∵AB⊥平面ACD,DE⊥平面ACD,
∴DE∥AB,又DE=2AB,∴AB∥MF,AB=MF,
∴四边形ABMF是平行四边形,
∴AF∥BM,∵AF 平面BCE,BM 平面BCE,
∴AF//平面BCE;
(2)∵AB⊥平面ACD,AF 平面ACD,
∴AB⊥AF,∴四边形ABMF是矩形,∴BM⊥MF.
∵△ACD是正三角形,F是CD中点,∴CD⊥AF.
∵BM∥AF,∴CD⊥BM,
∵MF∩CD=F,MF 平面CDE,CD 平面CDE,
∴BM⊥平面CDE,∵BM 平面BCE,
∴平面BCE⊥平面CDE;
(3)取线段DE的中点P,连接BP,
∵AB∥DP且AB=DP,
∴四边形ABPD是平行四边形,
∴AD∥BP,
则直线AD和平面BCE所成的角就是直线BP和平面BCE所成的角,
过点P作PN⊥CE,垂足为N,连结BN,
由(2)知平面BCE⊥平面CDE,又平面BCE∩平面CDE=CE,
∴PN⊥平面BCE,∴∠PBN为直线BP和平面BCE所成角的平面角.
设AB=1,则DE=AC=CD=AD=2,
∵DE⊥平面ACD,
∴DE⊥DC,
∵CD=DE,
∴,
∵PN⊥CE,EP=1,
∴,
∵四边形ABPD为平行四边形,
∴BP=AD=2,
∴,
故直线AD和平面BCE所成的角正弦值为.
【分析】(1)根据题意可得AF∥BM,结合线面平行的判定定理分析证明;
(2)根据题意题意可证BM⊥平面CDE,结合面面垂直的判定定理分析证明;
(3)根据(2)可知PN⊥平面BCE,则∠PBN为直线BP和平面BCE所成角的平面角,分析运算即可.
9.【答案】(1)证明:在正方体中,
因为平面平面,
平面
(2)证明:在正方体中,
易知平面中,又因为平面,
所以,
又因为平面,
所以平面,
又因为平面,
所以平面平面.
【解析】【分析】 (1) 根据题意可得 ,进而结合线面平行的判定定理分析证明;
(2)根据题意可证 平面, 进而结合面面垂直的判定定理分析证明.
10.【答案】(1)证明:因为底面是正方形,所以,
平面,平面,所以平面,
又因为平面与交于点,平面,平面平面,
所以.
(2)证明:侧面为等腰直角三角形,且,即,,
因为,,且两直线在平面内,可得平面,
因为平面,则.
又因为,,且两直线在平面内,
则平面,
因为平面,则,
因为,所以为等腰三角形,所以点为的中点.
又因为,所以为等腰直角三角形,
因为,所以AP⊥面,
因为面APD,所以面APD⊥面.
【解析】【分析】(1)根据线面平行可得 平面, 再结合线面平行的性质定理分析证明;
(2)根据题意可证 平面, 可得 ,同理可证 ,进而可得AP⊥面, 结合面面垂直的判定定理分析证明.
11.【答案】(1)解:在正方体,且,
∴为平行四边形,∴,∵平面,平面
∴平面;
(2)解:∵正方体,底面ABCD,底面ABCD,∴,
∵正方形ABCD中,,又∵平面,平面,,
∴平面;
【解析】【分析】(1)根据正方体的性质可得 , 进而结合线面平行的判定定理分析证明;
(2)根据正方体的性质可得 ,, 进而结合线面垂直的判定定理分析证明
12.【答案】(1)证明:取的中点,连接,
因为分别是的中点,
所以,且,
又是的中点,所以,且,
所以,且,
所以是平行四边形,故.
又平面,平面,
所以平面.
(2)因为底面,底面,
所以.
取中点,连接,
因为是矩形,且,
所以都是正方形,
所以,即.
又是平面内的两条相交直线,
所以平面.
而平面,所以平面平面.
【解析】【分析】 (1)取的中点,连接, 根据平行性质可得 ,结合线面平行的性质定理分析证明;
(2) 根据题意先证 平面,再结合面面垂直的判定定理分析证明.
13.【答案】(1)∵和分别是和的中点,
∴,
而平面平面,
∴平面.
∵,
∴四边形是平行四边形.
∴,而平面平面,
∴平面.
而平面平面,
∴平面平面.
【解析】(1)因为 , 平面底面,平面底面,平面,
所以 底面.
【分析】(1)根据题意利用面面垂直的性质定理分析证明;
(2)根据题意可证 , ,结合面面平行的判定定理分析证明.
14.【答案】(1)连接 交于点,连接 ,则是中点,又 D是的中点 ,,又, , ;
(2)过点作,又平面⊥平面 ,平面平面,平面,平面,
平面,,
由直三棱柱性质知平面,又平面,,
又平面 ,平面 ,,平面,
平面, .
【解析】【分析】 (1) 、连接 交于点,连接 ,通过证明得到 ;
(2) 、过点作,通过证明和得到平面,进而证明.
15.【答案】(1)在图2中取线段中点,连接、,如图所示:
由图1可知,四边形是矩形,且,
∴是线段与的中点,∴且,
图1中且,而且.
所以在图2中,且,
∴且,
∴四边形是平行四边形,则,
由于平面,平面,
∴平面.
(2)∵,,,面,,∴平面,
,
所以,
即三棱锥的体积为.
【解析】【分析】(1)取线段中点,连接、,通过证明四边形是平行四边形得到,再结合线面平行的判定定理可得证明;
(2)由已知可证明平面,再利用等体积法,即,先求出,再利用锥体体积公式计算即可.
16.【答案】(1)证明:由底面ABCD,底面ABCD,则,
在直角梯形中,,则,
又,平面,所以平面;
(2)解:平面,证明如下:
如图:
取PA中点E,连接ME,DE,由于M是PB的中点,故,且,
由,则,且,
从而四边形是平行四边形,故,
又平面,平面,所以平面;
(3)解:作,垂足为N,连接BN,如图:
在中,,又,所以≌,可得,
则≌,故,故为所求二面角的平面角,
由(1)知平面,由平面,可得,
在中,,所以,
在等腰三角形中,,所以,
因为,在中,由余弦定理得,
所以二面角的余弦值为.
【解析】【分析】(1)由底面ABCD,推出,再由为直角梯形,推出,结合线面垂直的性质及判定定理即可证明;
(2) 取中点E,连接ME,DE, 根据已知条件,再利用线面平行的判定定理即可证明;
(3) 作,垂足为N,连接BN, 易知,,确定为二面角的平面角,由(1)推出,在和等腰三角形中求出以及得长度,最后利用余弦定理求二面角的余弦值即可.
17.【答案】(1)证明:以点A为坐标原点,建立如图所示的空间直角坐标系,设,
由几何关系有:,
则直线的方向向量为:,,
设平面的法向量,则:,
据此可得:平面的一个法向量为,
结合可知:,即
据此可得:平面.
(2)解:因为平面ABCD,E为PD的中点.,
所以点E到平面ABCD的距离为,
因为三棱锥的体积是,
所以有,
结合(1)的结论可知:,
则平面的一个法向量为.
由平面可知平面的一个法向量为:,
据此可得:,
则,
观察可知二面角的平面角为锐角,
故二面角的余弦值为.
【解析】【分析】(1)以点A为坐标原点, 建立空间直角坐标系,设,,求出平面的法向量, 利用空间向量数量积计算得,所以平面 ;
(2) 由三棱锥的体积是,推出,由题意得出平面的一个法向量为 , 平面的一个法向量为, 根据空间向量夹角公式,计算求解即可.
18.【答案】(1)证明:如图,
因为N,P分别是AB,的中点,
所以,
又 平面, 平面,
所以 平面,
又M是的中点,
所以,
所以四边形是平行四边形,
所以,
又 平面, 平面,
所以 平面,
因为,
所以平面平面;
(2)解:连接,交于T,连接MT,
因为 ,底面是等边三角形,
所以四边形是正方形,
所以,且T为的中点,
又,
所以,
因为,平面,所以 平面 .
【解析】【分析】(1)分别证明平面,平面,利用面面平行的判定定理证明即可;
(2)连接,交于T,连接MT,分别证明,,结合线面垂直的判定定理可得证明.
19.【答案】(1)解:∵正四棱台中,,,
∴,又∵,
∴,∴四边形为平行四边形,
∴,又∵平面,平面,
∴平面,
∵,平面,平面,∴平面,
又∵,平面,平面,
∴平面平面,
∵平面,∴平面.
(2)解:在等腰梯形中作交于点,
由(1)知,,∴,
∴就是异面直线与所成的角,
∵,,
∴中,,,
∴,
∴异面直线与所成的角的余弦值为.
【解析】【分析】(1)根据面面平行的判定定理可得 平面平面, 结合面面平行的性质可得 平面.
(2)根据题意可知 就是异面直线与所成的角, 结合余弦定理运算求解.
20.【答案】(1)证明:如图,连接,设与相交于点,连接,
因为四边形是正方形,则为的中点,又为的中点,
于是,,即四边形为平行四边形,则,
而平面,平面,
所以平面.
(2)解:取的中点,连接,因为,且,
则四边形都为平行边形,有,
于是四边形为平行四边形,即有,
而为上靠近点的四等分点,则为的中点,又为的中点,则,
因此,又平面,平面,则平面,
显然,又平面,平面,则平面,
而平面,
所以平面平面.
【解析】【分析】(1)先证明,再利用线面平行的判定定理即可得证;
(2)先证明平面和平面,利用面面平行的判定定理即可得证.
21.【答案】(1)证明:如图,连接交于点,连接.
∵为的中点,为的中点,
∴为的中位线,
∴.
又∵平面,平面,
∴平面
(2)证明:连接,,连接交于点,连接,如图.
在正方体中,,
∵平面,平面,
∴平面.
又为的中位线,
∴.
∵平面,平面,
∴平面.
又∵平面,平面,,
∴平面平面.
∵平面,
∴平面.
【解析】【分析】 (1) 根据题意可得,进而结合线面平行的判定定理分析证明;
(2) 根据题意可得平面,平面,进而可得平面平面,结合面面平行的性质定理分析证明.
22.【答案】(1)解:多面体不是棱柱.理由如下:
因为棱柱的侧面必为平行四边形,故棱柱的面至少有3个平行四边形,而多面体只有1个面是平行四边形,故不是棱柱.
(2)解:易知三棱柱的体积,
三棱锥的体积,
易知三棱锥的体积等于三棱锥的体积,
故多面体的体积.
(3)解:因为D,E分别是,AC的中点,所以,
所以四边形为平行四边形
所以.又平面,平面,所以平面.
易知,得四边形为平行四边形.
所以,又平面,平面,所以平面.
而,BE,平面,
所以平面平面.
【解析】【分析】(1)利用已知条件和棱柱的概念判断即可;
(2)利用间接法求多面体的体积,即;
(3)利用已知条件可证得四边形BB1DE和四边形ADC1E都是平行四边形,进而得到 , ,利用线面平行的判定定理可得: 平面 , 平面 ,再利用面面平行的判定定理即可得证.
23.【答案】(1)解:多面体为二十四等边体知、、、、、为正方体对应棱上的中点
则,,
,平面,,平面,
则平面平面.
(2)解:正方体的体积,
截去的每个四面体体积为,
所以石凳所对应几何体的体积为.
【解析】【分析】(1)由面面平行的判定定理即可证明.
(2)先求出八个全等的三棱锥的体积和,再利用正方体的体积减去截去的部分体积即可算出.
24.【答案】(1)证明:取的中点,取上靠近的四等分点,连接,
,
且,
,
且,
且,
四边形是平行四边形,
,又平面,平面,
平面,
,
,
又平面平面,
平面,
平面
平面平面.
(2)解:由(1)知,又底面,
底面,连接,
就是与底面所成的角.
在中,,
,
,
与底面所成角的大小是.
【解析】【分析】 (1)根据比例关系可得线线平行,由此可得线面平行,再由面面平行的判定定理得证平面平面.
(2)根据线面角的定义得出就是与底面所成的角.再求解即可得直线与底面所成角的大小.
25.【答案】(1)证明:因为MB//NC,MB 面DNC,NC 面DNC,
所以MB//面DNC.因为AMND是矩形,所以MA//DN,又MA 面DNC,
DN 面DNC,所以MA//面DNC.又MA∩MB=M,且MA、MB 平面AMB,所以面AMB//面DNC.
(2)证明:因为AMND是矩形,所以AM⊥MN.
因为面AMND⊥面MBCN,且面AMND∩面MBCN=MN,AM 面AMND,
所以AM⊥平面MBCN,而BC 平面MBCN,所以AM⊥BC.
因为MC⊥BC,MC∩AM=M,MC、AM 面AMC,所以BC⊥面AMC,
因为AC 面AMC,所以BC⊥AC.
【解析】【分析】(1)由线面平行的判定可证MB//面DNC、MA//面DNC,再用面面平行的判定证结论;
(2)由面面垂直的性质得AM⊥平面MBCN,再由线面垂直的性质、判定证BC⊥面AMC,最后由线面垂直的性质证线线垂直即可.
26.【答案】(1)证明:连结,,
因为正方体,所以,且,
所以四边形为平行四边形,
所以,平面,平面,
所以平面,
取中点,连结,
因为是和的中点,
所以,,
且,,
所以,且,
所以四边形为平行四边形,
所以,且,
因为,且,
所以四边形为平行四边形,
所以,且,
所以,平面,平面,
所以平面,,平面,平面,
所以平面平面,平面,所以平面,
(2)解:因为正方体,
所以点到平面的距离与点到平面的距离相等,
所以三棱锥的高,
所以
【解析】【分析】
(1)可以通过证明面面平行进而得到线面平行
(2)根据正方体的的体积特点,得出体积之间的数量关系,从而得出高和几何体的体积.
27.【答案】(1)证明:
方法1:
在棱上取,使得,连接.
因为,所以,且.
当时,,则,且,
所以,
所以四边形是平行四边形,所以.
又因为平面平面,
所以平面.
方法2:
在棱上取,使得,连接.
因为,所以
又平面,平面,所以平面.
又因为,且,所以四边形是平行四边形,
所以,又平面,平面,从而平面.
因为平面,所以平面平面,
因为平面
所以平面.
(2)解:取的中点,则.分别以射线为轴的正半轴建立空间直角坐标系,如图所示,
则,所以.
因为,所以,所以.
设是平面的法向量,
则,可取.
不难得到:平面的一个法向量为.
所以,化简得:,
解得,或.因为,所以.
【解析】【分析】 (1) 方法一:在棱上取,使得,连接,根据平行的性质可证,进而可得结果;方法二:在棱上取,使得,连接,先证平面平面,根据面面平行的性质可得结果;
(2) 分别以射线为轴的正半轴建立空间直角坐标系,求平面的法向量,根据面面夹角的向量求法可得结果.
28.【答案】(1)证明:在矩形ABCD中,.
因为平面CDE,平面CDE,
所以平面CDE.
因为平面ABCD,平面ABCD,
所以.
因为平面CDE,平面CDE,
所以平面CDE.
又因为平面PAB,平面PAB,.
所以平面平面CDE.
因为平面PAB,
所以平面CDE.
(2)解:因为平面ABCD,平面ABCD,平面ABCD,
所以,.
又因为ABCD是矩形,,
所以AD,AB,PA两两垂直,如图建立空间直角坐标系,
则,,,
所以,.
设平面PEC的一个法向量为,则
,即.
令,则,.
于是.
取平面PEA的法向量为.
则.
由图可知二面角为锐角,
所以二面角的余弦值是.
(3)解:令线段AF的长为t,则,.
所以,
因为点F到平面PCE的距离.
所以,即.
解得或(舍).
所以线段AF的长为.
【解析】【分析】(1) 通过证明平面平面 ,从而证明 平面;
(2) 先证明,,两两垂直,建立空间直角坐标系,利用空间向量求二面角的余弦值;
(3)设线段的长为,则,利用点到平面距离公式列方程,求出即可.
29.【答案】(1)证明:连A1C1交B1D1于点F,连EF,
∵A1B1C1D1是菱形,∴F是A1C1中点,∵E是AA1中点,∴EF∥AC1,
∵EF 平面B1D1E,AC1 平面B1D1E,∴AC1∥平面B1D1E.
(2)解:过B1作B1H⊥D1A1的延长线于点H,
由AA1⊥底面ABCD知AA1⊥平面A1B1C1D1,则AA1⊥B1H,又AA1∩1A1=A1,B1H⊥平面AA1D1D.
由∠A1B1C1=∠ABC=60°知∠B1A1H=60°,
又A1B1=2,则.
(3)解:∵AA1⊥平面ABCD,平面A1B1C1D1∥平面ABCD,
∴AA1⊥平面A1B1C1D1,∵B1D1 平面A1B1C1D1,∴B1D1⊥AA1,
∵菱形A1B1C1D1中B1D1⊥A1C1,A1C1∩AA1=A1,A1C1,AA1 平面AA1C1,
∴B1D1⊥平面AA1C1,又AC1 平面AA1C1,∴AC1⊥B1D1,
过F在Rt△AA1C1中,作FM⊥AC1,垂足为M,
则由FM∩B1D1=F,FM,B1D1 平面MB1D1知AC1⊥平面MB1D1,
∴存在M满足条件,在Rt△AA1C1中,AA1=A1C1=2,,F是A1C1中点,
∴,∴.
【解析】【分析】(1)连A1C1交B1D1于点F,连EF,通过中位线证明EF∥AC1,得到AC1∥平面B1D1E;
(2)过B1作B1H⊥D1A1的延长线于点H,得到B1H⊥平面AA1D1D,所以 ,进而求解;
(3)由AA1⊥平面ABCD和菱形A1B1C1D1得到B1D1⊥平面AA1C1,所以AC1⊥B1D1,则过F作FM⊥AC1,垂足为M,有AC1⊥平面MB1D1,再求解.
30.【答案】(1)证明:∵四边形,都是矩形,
∴,,∴四边形是平行四边形,
∴,∵平面,∴平面;
(2)证明:连接,设,∵平面平面,且,
∴平面,∴,
又,∴四边形为正方形,∴,
∴平面,又平面,∴,
(3)解:设,则,其中,
由(1)得平面,
∴四面体的体积为:
,
时,四面体的体积最大,其最大值为2.
【解析】【分析】(1) 连接,设,利用平面平面,且结合面面垂直的性质对立证出线面垂直,所以平面,再利用线面垂直的定义证出线线垂直,所以,再利用,所以四边形为正方形,所以,再利用线线垂直证出线面垂直,所以平面,再利用线面垂直的定义证出线线垂直,从而证出。
(2) 设,则,其中,由(1)得平面,再利用三棱锥的体积公式和二次函数的图象求最值的方法得出四面体的体积的最大值。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
