高中数学人教A版(2019)必修2 9.1 随机抽样 选择题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 9.1 随机抽样 选择题专项章节综合练习题(答案+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 08:51:25 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
9.1 随机抽样 选择题专项
一、选择题
1.(2023高一下·定远期末)某社区有个家庭,其中高收入家庭户,中等收入家庭户,低收入家庭户为了调查社会购买力的某项指标,要从中抽取一个容量为户的样本,记作;某学校高一年级有名女运动员,要从中选出人调查学习负担情况,记作那么完成上述两项调查应采用的抽样方法是( )
A.用简单随机抽样法,用分层随机抽样法
B.用简单随机抽样法,用简单随机抽样法
C.用分层随机抽样法,用简单随机抽样法
D.用分层随机抽样法,用分层随机抽样法
2.已知总体容量为108,若用随机数表法抽取一个容量为10的样本,下列对总体的编号正确的是( )
A.1,2,…,108 B.01,02,…,108
C.00,01,…,107 D.001,002,…,108
3.某学校为了调在学生的学习情况,从每班随机抽取5名学生进行调查.若一班有45名学生,将每一学生从01到45编号,请利用下面的随机数表选取5个编号,选取方法是从随机数表的第2行的第7、8列开始由左向右依次选取两个数字(作为编号),如果选取的两个数字不在总体内,则将它去掉,直到取足样本,则第四个编号为( )
附随机数表(下面为随机数表的前3行):
03 47 43 73 86 36 96 47 36 61 46 98 63 71 62 33 26 16 80 45 60 11 14 10 95
97 74 24 67 62 42 81 14 57 20 42 53 32 37 32 27 07 36 07 51 24 51 79 89 73
16 76 62 27 66 56 50 26 71 07 32 9079 78 53 13 55 38 58 59 88 97 54 14 10
A.32 B.37 C.42 D.24
4.(2022高一下·常德期末)某校为更好地支持学生个性发展,开设了学科拓展类、创新素质类、兴趣爱好类三种类型的校本课程,每位同学从中选择一门课程学习.现对该校6000名学生的选课情况进行了统计,如图①,并用分层抽样的方法从中抽取的学生对所选课程进行了满意率调查,如图②.
则下列说法错误的是( )
A.抽取的样本容量为120
B.该校学生中对兴趣爱好类课程满意的人数约为1050
C.若抽取的学生中对创新素质类课程满意的人数为36,则
D.该校学生中选择学科拓展类课程的人数为1500
5.(2022高一下·江岸期末)某沙漠地区经过治理,生态系统得到很大改善,野生动物有所增加,为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,计划从这些地块中抽取20个作为样本,根据现有的统计资料,各地块间植物覆盖面积差异很大,为了让样本具有代表性,以获得该地区这种野生动物数量准确的估计,在下面的抽样方法中,最合理的抽样方法是( )
A.普查 B.分层抽样
C.简单随机抽样 D.非以上三种抽样方法
6.(2022高一下·电白期末)下列问题中最适合用简单随机抽样方法的是( )
A.某学校有学生1 320人,卫生部门为了了解学生身体发育情况,准备从中抽取一个容量为300的样本
B.为了准备省政协会议,某政协委员计划从1 135个村庄中抽取50个进行收入调查
C.从全班30名学生中,任意选取5名进行家访
D.为了解某地区癌症的发病情况,从该地区的5 000人中抽取200人进行统计
7.(2022高一下·保定期末)某社区卫生室为了了解该社区居民的身体健康状况,对该社区2000名男性居民和1600名女性居民按性别采用等比例分层随机抽样的方法进行抽样调查,抽取了一个容量为180的样本,则应从女性居民中抽取的人数为( )
A.60 B.80 C.90 D.100
8.(2022高二下·宁波期末)在“2022年北京冬季奥运会”闭幕后,某中学学生会对本校高一年级1000名学生收看比赛的情况用随机抽样方式进行调查,样本容量为50,将数据分组整理后,列表如下:
观看场数 0 1 2 3 4 5 6 7
观看人数占调查人数的百分比 8% 10% 20% 26% 12% 6% 2%
从表中可以得出正确的结论为( )
A.表中m的数值为8
B.估计观看比赛场数的中位数为3
C.估计观看比赛场数的众数为2
D.估计观看比赛不低于4场的学生约为720人
9.(2022高一下·吉林期中)关于统计数据的分析,有以下几个结论:①一组数不可能有两个众数;②将一组数据中的每个数据都减去同一个数后,方差发生变化;③调查剧院中观众的观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层抽样;④一组数据的方差一定是正数;⑤如图所示是随机抽取的200辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在[50,60]的汽车大约是60辆.
则这五种说法中错误的个数是( )
A.1 B.3 C.4 D.5
10.(2021高二上·丰台期末)抛掷一枚质地均匀的硬币,设事件“正面向上”,则下列说法正确的是( )
A.抛掷硬币10次,事件A必发生5次
B.抛掷硬币100次,事件A不可能发生50次
C.抛掷硬币1000次,事件A发生的频率一定等于0.5
D.随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小
11.某学校为了解学生对乒乓球、羽毛球运动的喜爱程度,用按比例分配的分层随机抽样法从高一、高二、高三年级所有学生中抽取部分学生做抽样调查,已知该学校高一、高二、高三年级学生人数的比例如图所示,若抽取的样本中高三年级的学生有45人,则样本容量为( )
A.125 B.100 C.150 D.120
12.(2023高三上·开远月考)某学校共有980名学生,其中高一的学生有400名,高二的学生有300名,其余都是高三的学生,为了解该校学生的体育锻炼时间,按照高一 高二 高三三个级段进行分层抽样,如果样本容量为196,那么应在高三的学生中抽取( )
A.48名 B.52名 C.56名 D.60名
13.“五月榴花妖艳烘,绿杨带雨垂垂重,五色新丝缠角粽”,这是欧阳修在《渔家傲·五月榴花妖艳烘》中描写端午节的诗句.某商家为迎接端午节,计划将粽子以“粽情粽意”礼盒形式进行销售,现利用分层随机抽样从72个蛋糕肉粽、18个碱水粽、36个豆沙粽、54个莲子粽中随机抽取10个粽子放入一个礼盒中作为展开进行试销售,则该礼盒中莲子粽的个数为( )
A.2 B.1 C.4 D.3
14.(2023高一下·湖南期末)某学校高一年级、高二年级、高三年级分别有学生800人、950人、1050人,学校为了调研学情,用分层抽样的方法从中抽取56人,则高三年级应该抽取的人数为( )
A.21 B.19 C.16 D.18
15.(2023高一下·河北期末)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样作抽样调查,拟从初中部和高中部两层共抽取名学生,已知该校初中部和高中部分别有和名学生,则正确的( )
A.高中部产生个样本
B.初中部产生个样本
C.不同级部每个学生被抽取的可能性不相同
D.可以从两个级部各抽取个样本
16.(2023高一下·联合期末)唐代以来,牡丹之盛,以“洛阳牡丹甲天下”的美名流传于世.唐朝诗人白居易“花开花落二十日,一城之人皆若狂”和刘禹锡“唯有牡丹真国色,花开时节动京城”的诗句正是描写洛阳城的景象.已知根据花瓣类型可将牡丹分为单瓣类、重瓣类、千瓣类三类,现有牡丹花n朵,千瓣类比单瓣类多30朵,采用分层抽样方法从中选出12朵牡丹进行观察研究,其中单瓣类有4朵,重瓣类有2朵,千瓣类有6朵,则n=( )
A.360 B.270 C.240 D.180
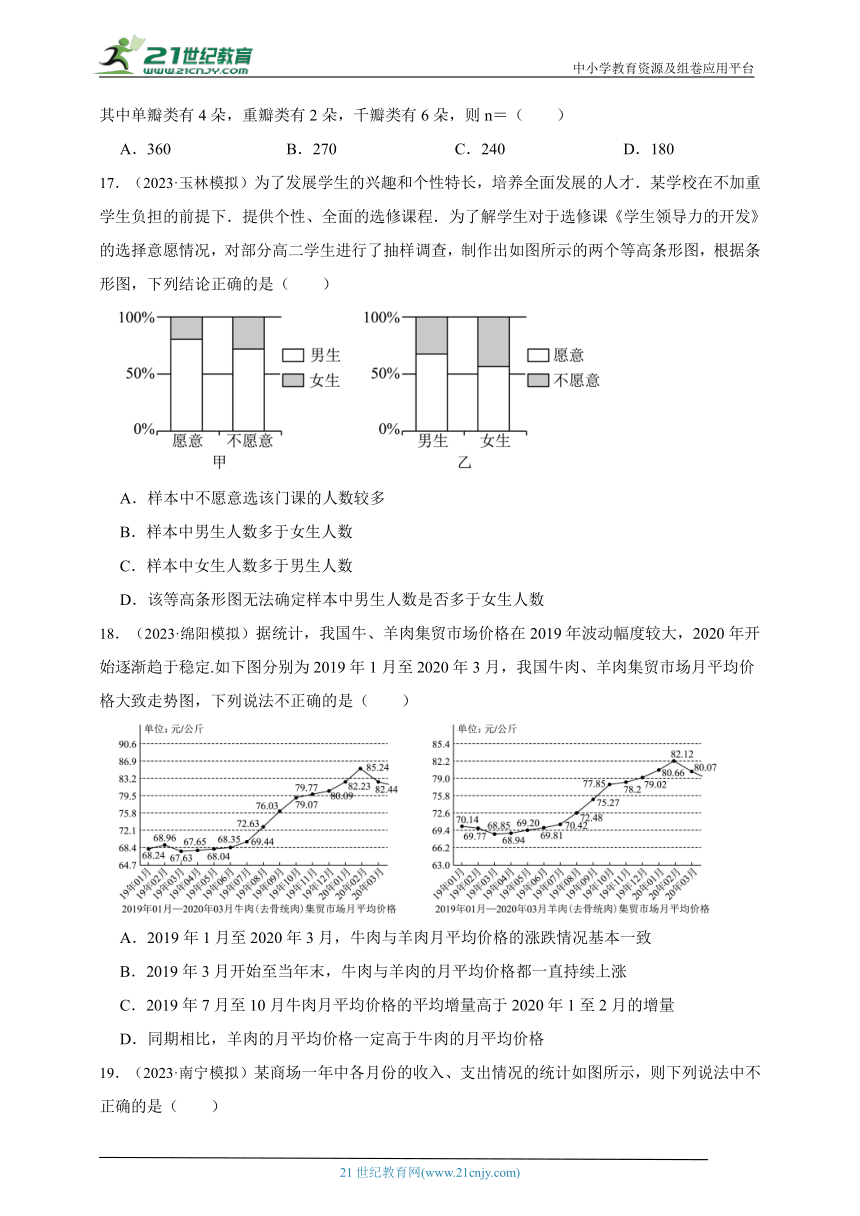
17.(2023·玉林模拟)为了发展学生的兴趣和个性特长,培养全面发展的人才.某学校在不加重学生负担的前提下.提供个性、全面的选修课程.为了解学生对于选修课《学生领导力的开发》的选择意愿情况,对部分高二学生进行了抽样调查,制作出如图所示的两个等高条形图,根据条形图,下列结论正确的是( )
A.样本中不愿意选该门课的人数较多
B.样本中男生人数多于女生人数
C.样本中女生人数多于男生人数
D.该等高条形图无法确定样本中男生人数是否多于女生人数
18.(2023·绵阳模拟)据统计,我国牛、羊肉集贸市场价格在2019年波动幅度较大,2020年开始逐渐趋于稳定.如下图分别为2019年1月至2020年3月,我国牛肉、羊肉集贸市场月平均价格大致走势图,下列说法不正确的是( )
A.2019年1月至2020年3月,牛肉与羊肉月平均价格的涨跌情况基本一致
B.2019年3月开始至当年末,牛肉与羊肉的月平均价格都一直持续上涨
C.2019年7月至10月牛肉月平均价格的平均增量高于2020年1至2月的增量
D.同期相比,羊肉的月平均价格一定高于牛肉的月平均价格
19.(2023·南宁模拟)某商场一年中各月份的收入、支出情况的统计如图所示,则下列说法中不正确的是( )
A.支出最高值与支出最低值的比是6:1
B.利润最高的月份是2月份
C.第三季度平均收入为50万元
D.1~2月份的支出的变化率与10~11月份的支出的变化率相同
20.(2023·宜宾模拟)2月国家统计局发布中华人民共和国2022年国民经济和社会发展统计公报.下图1是2018-2022年国内生产总值及其增长速度,图2是2018-2022年三次产业增加值占国内生产总值比重(三次产业包括第一产业,第二产业,第三产业).根据图1,图2,以下描述不正确的是( )
A.2018-2022年国内生产总值呈逐年增长的趋势
B.2020年与2022年国内生产总值的增长速度较上一年有明显回落
C.2018-2022年第三产业增加值占国内生产总值比重的极差为1.7%
D.2020年第二产业增加值较2019年有所减少
21.(2023·广东模拟)如图所示是中国2012-2021年汽车进 出口量统计图,则下列结论错误的是( )
A.2012-2021年中国汽车进口量和出口量都是有增有减的
B.从2018年开始,中国汽车的出口量大于进口量
C.2012-2021年中国汽车出口量的第60百分位数是106万辆
D.2012-2021年中国汽车进口量的方差大于出口量的方差
22.(2023·江苏会考)党的二十大报告指出:“全面提高人才自主培养质量,着力造就拔尖创新人才,聚天下英才而用之.”某区域教育部门为提高学生的创新能力,组织了200名学生参与研究性学习,每人仅参加1个课题组,参加各课题组的人数占比的扇形统计图如图所示,则参加数学类的人数比参加理化类的人数多( )
A.16 B.30 C.32 D.62
23.(2023高二上·朝阳开学考)某市6月前10天的空气质量指数为35,54,80,86,72,85,58,125,111,53,则这组数据的第70百分位数是( )
A.86 B.85.5 C.85 D.84.5
24.某校为了解本校高三学生学习心里状态,采用系统抽样方法从80人中抽取40人参加某种测试,为此将题目随机编号1,2,,800,分组后在第一组采用简单随机抽样的方法抽到号码为18,抽到的40人中,编号落入区间的人做试卷,编号落入区间的人做试卷,其余的人做试卷,则做试卷的人数为( )
A.10 B.12 C.18 D.28
25.(2023高二上·柳州开学考)某新闻机构想了解全国人民对《长津湖之水门桥》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本,若3个区人口数之比为2:3:4,且人口最少的一个区抽出100人,则这个样本的容量为( )
A.550 B.500 C.450 D.400
26.(2023高二上·昆明开学考)某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时:③若从每周使用时间在,三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( )
A.①② B.①③ C.②③ D.①②③
二、多项选择题
27.一组数据:,,,,,,,则( )
A.这组数据的平均数为 B.这组数据的方差为
C.这组数据的极差为 D.这组数据的第百分位数为
三、填空题
28.(2023高一下·湖州期末)已知采用分层抽样得到的高三男生、女生各100名学生的身高情况为:男生样本平均数为172cm,方差为120,女生样本平均数165cm,方差为120,则总体样本方差是 .
29.数据,,的方差为,则数据,,的平均数为 .
30.下列叙述中正确的是 .(填写所有正确命题的序号)
①随机从某校高一600名男生中抽取60名学生调查身高,该调查中样本量是60
②数据2,3,3,5,9,9的中位数为3和5,众数为3和9
③数据9,10,11,11,16,20,22,23的75%分位数为21
④若将一组数据中的每个数都加上2,则平均数和方差都没有发生变化
答案解析部分
1.【答案】C
【解析】【解答】 ①社区中各个家庭收入差别明显,应该用分层随机抽样法;②由于样本量不大,且抽取的人数较少,故采用简单随机抽样法.
故选: C.
【分析】 根据分层抽样,简单随机抽样的定义进行判断,即可得答案.
2.【答案】D
【解析】【解答】用随机数表法选取样本时,样本的编号位数要一致,
故总体容量为108,用随机数表法抽取一个容量为10的样本,对总体的编号为001,002,…,108
故答案为:D
【分析】利用已知条件结合随机数表法,进而得出对总体的编号正确的选项。
3.【答案】A
【解析】【解答】解:根据题意,用随机数表抽取的样本为42、14、20、32,
则第四个编号为32;
故答案为:A
【分析】根据随机数表法的读取方法,依次读取,即可求解出答案.
4.【答案】C
【解析】【解答】抽取的样本容量为,A正确,不符合题意;
该校学生中对兴趣爱好类课程满意的人数约为,B正确,不符合题意;
根据题意,创新素质类课程的满意率为,,C错误,符合题意;
该校学生中选择学科拓展类课程的人数为,D正确,不符合题意.
故答案为:C.
【分析】根据学校人数和抽样比例即可求出样本容量,根据学校总人数结构统计图逐一判断即可.
5.【答案】B
【解析】【解答】解:因为所研究的总体中差异很大,为了让样本具有代表性,最合理的抽样方法是分层抽样.
故答案为:B.
【分析】 根据所研究的对象差异性很大,要使样本具有代表性,最合理的抽样方法是分层抽样.
6.【答案】C
【解析】【解答】对于A,不同年级的学生身体发育情况差别较大,适合用分层抽样,A不是;
对于B,总体容量较大,并且各村庄人口、地域、发展等方面的差异,不宜用简单随机抽样,B不是;
对于C,总体容量较小,个体之间无明显差异,适宜用简单随机抽样;
对于D,总体容量较大,不同年龄的人癌症的发病情况不同,不宜用简单随机抽样,D不是.
故答案为:C
【分析】利用已知条件结合简单随机抽样的方法,进而找出正确的答案。
7.【答案】B
【解析】【解答】应从女性居民中抽取的人数为
故答案为:B
【分析】根据分层抽样按比例抽取计算可得答案.
8.【答案】B
【解析】【解答】对A,由频率分布表的性质,得:m=100﹣8﹣10﹣20﹣26﹣12﹣6﹣2=16,故A错误;
对B,因为,,故中位数为3,故B正确;
对C,因为观看场数为3占的比例最高,故观看比赛场数的众数为3;
对D,观看比赛不低于4场的学生所占比率为:16%+12%+6%+2%=36%,
∴估计观看比赛不低于4场的学生约为:1000×36%=360人,故D错误;
故答案为:B.
【分析】由随机抽样的调查结果,结合图表的性质以及中位数和众数公式代入数值计算出结果即可。
9.【答案】C
【解析】【解答】解:对于①,若一组数据中有多个不同的数出现的次数相同且均出现次数最多,则几个数均为该组数据的众数,①错误;
对于②,将一组数据中每个数据都减去同一个数后,平均数也减去同一个数,则方差不变,②错误;
对于③,从50排(每排人数相同)中任意抽取一排的人进行调查,每排被抽到的概率均相同,属于简单随机抽样,③错误;
对于④,若一组数据都是完全相等的数,则该组数据方差为0,④错误;
对于⑤,由频率分布直方图可知:时速在[50,60]的频率为0.03×10=0.3,则时速在[50,60]的汽车大约有200×0.3=60辆,⑤正确.
故选:C.
【分析】由众数定义、方差的性质、抽样方法和频率分布直方图计算频数的方法依次判断各个选项即可.
10.【答案】D
【解析】【解答】不管抛掷硬币多少次,事件A发生的次数是随机事件,ABC不符合题意;
随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小;
故答案为:D
【分析】根据已知条件,结合随机事件的概率及及性质逐项进行分析,可得答案。
11.【答案】A
【解析】【解答】解:由扇形统计图可知,高三年级的学生占总人数的36%,而抽取的样本中高三年级的学生人数为45人,所以样本容量为人.
故答案为:A.
【分析】根据分层抽样中,抽样比相同根据抽取的样本中高三年级的人数即可求得样本容量.
12.【答案】C
【解析】【解答】解:高三的学生有, 应在高三的学生中抽取名.
故答案为:C.
【分析】根据分层抽样分析运算即可.
13.【答案】D
【解析】【解答】解:依题意得,莲子粽在礼盒中的比例为,
则该礼盒中莲子粽的个数为.
故答案为:D.
【分析】根据分层抽样定义可得莲子粽在礼盒中的比例,从而可计算个数得出结论.
14.【答案】A
【解析】【解答】解:高三年级应该抽取的人数为.
故答案为:A.
【分析】根据分层抽样的性质列式计算求解.
15.【答案】A
【解析】【解答】解:根据已知条件,易知分层抽样的抽样比为,故该校初中部产生的样本容量为,高中部产生的样本容量为.
故答案为:A.
【分析】先利用分层抽样确定抽样比,再分别计算各部产生的样本容量即可.
16.【答案】D
【解析】【解答】设 单瓣类 有朵,则 千瓣类 有朵,
由题意可得,解得,
即单瓣类 有60朵,则 千瓣类 有90朵,
则,解得.
胡答案为:D.
【分析】根据题意结合分层抽样的抽样比不变列式求解.
17.【答案】B
【解析】【解答】对于A,由图乙可知,样本中男生,女生都大部分愿意选择该门课,
则样本中愿意选该门课的人数较多,A不符合题意;
对于BCD,由图甲可知,在愿意和不愿意的人中,都是男生占比较大,
所以可以确定,样本中男生人数多于女生人数,B符合题意,CD不符合题意.
故答案为:B.
【分析】根据等高条形图直接判断各个选项即可.
18.【答案】D
【解析】【解答】根据图像的大致走势即可判断牛肉与羊肉月平均价格的涨跌情况基本一致,A正确,不符合题意;
根据图像中的数据比较可知2019年3月开始至当年末,牛肉与羊肉的月平均价格,数据越来越大,都一直持续上涨,B正确,不符合题意;
2019年7月至10月牛肉月平均价格的平均增量为,2020年1至2月牛肉增量为,C正确,不符合题意;
2019年8月牛肉月平均价格为,2019年8月羊肉月平均价格为,所以同期相比,羊肉的月平均价格也可能会低于牛肉的月平均价格,D错误,符合题意.
故答案为:D.
【分析】根据图像数据分析即可求解.
19.【答案】B
【解析】【解答】支出最高值为60万元,支出最低值为10万元,支出最高值与支出最低值的比是,A正确,不符合题意;
2月份利润为20万元,3月份和10月份利润为30万元,利润最高的月份是3月份和10月份,B错误,符合题意;
7,8,9月份收入分别为40万元,50万元,60万元,则第三季度平均收入为50万元,C正确,不符合题意;
1~2月份的支出变化率为 ,10~11月份的支出变化率为 ,故变化率相同,D正确,不符合题意.
故答案为:B
【分析】由统计图中数据,对选项中的统计结论进行判断.
20.【答案】D
【解析】【解答】依题意,
对于A:由图1可以看出直方图逐年增高,所以2018-2022年国内生产总值呈逐年增长的趋势,A符合题意;
对于B:由图1可以看出折线在2020年与2022年时与上一年连线的斜率小于0,B符合题意;
对于C:由图2可以得出2018-2022年第三产业增加值占国内生产总值比重最大值为:54.5%,
最小值为:52.8%,所以极差,C符合题意;
对于D:结合图1图2可知,2019年第二产业的增加值为:亿元;
2020年第二产业的增加值为:亿元.
因为,所以2020年第二产业增加值较2019年有所增加,
D不符合题意.
故答案为:D.
【分析】根据给出的图形逐一分析判断即可.
21.【答案】D
【解析】【解答】由条形图可知2012-2021年中国汽车进口量和出口量都是有增有减的,所以A正确,不符合题意;
由条形图可知从2018年开始,中国汽车的出口量大于进口量,所以B正确,不符合题意;
2012-2021年中国汽车出口量由小到大排列为:,因此第60百分位数是,所以C正确,不符合题意;
由条形图可知2012-2021年中国汽车进口量的波动小于出口量的波动,因此2012-2021年中国汽车进口量的方差小于出口量的方差,所以D错误,符合题意,
故答案为:D
【分析】根据条形图,结合百分位数、方差的性质逐一判断即可.
22.【答案】C
【解析】【解答】由扇形统计图可知参加数学类的人数为,
参加理化类的人数为,
故参加数学类的人数比参加理化类的人数多,
故答案为:C
【分析】由扇形图计算参加数学类和理化类的人数,即可求得答案.
23.【答案】B
【解析】【解答】解:将这组数据从小到大排序为: 35,53,54,58,72,80,85,86,111,125,又,这组数据的第70百分位数是.
故答案为:B.
【分析】先将这组数据从小到大排列,再根据百分位数定义求解.
24.【答案】B
【解析】【解答】 ,
间隔为20.
故做试卷 与 的人数共为 ,
做问卷 的人数为 ,
故答案为:B.
【分析】利用已知条件结合系统抽样的方法,进而得出做试卷的人数。
25.【答案】C
【解析】【解答】解:设这个样本的容量为,则,求得.
故答案为:C.
【分析】根据分层抽样原理计算求解.
26.【答案】D
【解析】【解答】解:,求得, ①正确;
根据频率分布直方图计算估计出每周人使用手机时间为,②正确;
每周使用时间在,三组内的学生的比例为,根据分层样原理得选取8人进行访谈, 则应从使用时间在内的学生中选取的人数为3,③ 正确.
故答案为:D.
【分析】 ① 根据频率分布直方图中小矩形的面积和为1, ② 求出频率分布直方图的平均值,即为抽取100人的平均值的估计值, ③ 利用分层抽样计算出使用时间在 内的学生中选取的人数.
27.【答案】A,D
【解析】【解答】解:A、这组数据的平均数为:,A正确;
B、这组数据的方差为:,B错误;
C、这组数据的极差为:,C错误;
D、,第70百分位数是第5个数7,D正确.
故答案为:AD.
【分析】利用公式分别计算平均数、方差、极差、第70百分位数判断选项.
28.【答案】132.25
【解析】【解答】设总体平均数为,方差为,男生平均数为,方差为,女生平均数为,方差为,由题意得,,,,
故答案为:132.25
【分析】根据分层抽样原理,代入平均数和方差公式进行求解。
29.【答案】:7或
【解析】【解答】解:因为 方差为,解得,
所以数据,,的平均数为或.
故答案为:7或.
【分析】根据题意结合方差公式可得,结合平均数的性质运算求解.
30.【答案】①③
【解析】【解答】解:对于 ① : 随机从某校高一600名男生中抽取60名学生调查身高,该调查中样本量是60 ,故①正确;
对于② :中位数为, 众数为3和9 ,故②错误;
对于③ :因为,所以 75%分位数为 第6位数和第7位数的平均数,故 ③ 错误;
对于 ④ : 若将一组数据中的每个数都加上2, 则 平均数 加2,方差为原来的4倍,故 ④ 错误;
故答案为: ①③ .
【分析】对①:根据样本容量的概念分析判断;对② :根据中位数、众数的概念分析判断;对 ③ :根据百分位数的概念分析判断;对 ④ :根据平均数、方差的性质分析判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.1 随机抽样 选择题专项
一、选择题
1.(2023高一下·定远期末)某社区有个家庭,其中高收入家庭户,中等收入家庭户,低收入家庭户为了调查社会购买力的某项指标,要从中抽取一个容量为户的样本,记作;某学校高一年级有名女运动员,要从中选出人调查学习负担情况,记作那么完成上述两项调查应采用的抽样方法是( )
A.用简单随机抽样法,用分层随机抽样法
B.用简单随机抽样法,用简单随机抽样法
C.用分层随机抽样法,用简单随机抽样法
D.用分层随机抽样法,用分层随机抽样法
2.已知总体容量为108,若用随机数表法抽取一个容量为10的样本,下列对总体的编号正确的是( )
A.1,2,…,108 B.01,02,…,108
C.00,01,…,107 D.001,002,…,108
3.某学校为了调在学生的学习情况,从每班随机抽取5名学生进行调查.若一班有45名学生,将每一学生从01到45编号,请利用下面的随机数表选取5个编号,选取方法是从随机数表的第2行的第7、8列开始由左向右依次选取两个数字(作为编号),如果选取的两个数字不在总体内,则将它去掉,直到取足样本,则第四个编号为( )
附随机数表(下面为随机数表的前3行):
03 47 43 73 86 36 96 47 36 61 46 98 63 71 62 33 26 16 80 45 60 11 14 10 95
97 74 24 67 62 42 81 14 57 20 42 53 32 37 32 27 07 36 07 51 24 51 79 89 73
16 76 62 27 66 56 50 26 71 07 32 9079 78 53 13 55 38 58 59 88 97 54 14 10
A.32 B.37 C.42 D.24
4.(2022高一下·常德期末)某校为更好地支持学生个性发展,开设了学科拓展类、创新素质类、兴趣爱好类三种类型的校本课程,每位同学从中选择一门课程学习.现对该校6000名学生的选课情况进行了统计,如图①,并用分层抽样的方法从中抽取的学生对所选课程进行了满意率调查,如图②.
则下列说法错误的是( )
A.抽取的样本容量为120
B.该校学生中对兴趣爱好类课程满意的人数约为1050
C.若抽取的学生中对创新素质类课程满意的人数为36,则
D.该校学生中选择学科拓展类课程的人数为1500
5.(2022高一下·江岸期末)某沙漠地区经过治理,生态系统得到很大改善,野生动物有所增加,为调查该地区某种野生动物的数量,将其分成面积相近的200个地块,计划从这些地块中抽取20个作为样本,根据现有的统计资料,各地块间植物覆盖面积差异很大,为了让样本具有代表性,以获得该地区这种野生动物数量准确的估计,在下面的抽样方法中,最合理的抽样方法是( )
A.普查 B.分层抽样
C.简单随机抽样 D.非以上三种抽样方法
6.(2022高一下·电白期末)下列问题中最适合用简单随机抽样方法的是( )
A.某学校有学生1 320人,卫生部门为了了解学生身体发育情况,准备从中抽取一个容量为300的样本
B.为了准备省政协会议,某政协委员计划从1 135个村庄中抽取50个进行收入调查
C.从全班30名学生中,任意选取5名进行家访
D.为了解某地区癌症的发病情况,从该地区的5 000人中抽取200人进行统计
7.(2022高一下·保定期末)某社区卫生室为了了解该社区居民的身体健康状况,对该社区2000名男性居民和1600名女性居民按性别采用等比例分层随机抽样的方法进行抽样调查,抽取了一个容量为180的样本,则应从女性居民中抽取的人数为( )
A.60 B.80 C.90 D.100
8.(2022高二下·宁波期末)在“2022年北京冬季奥运会”闭幕后,某中学学生会对本校高一年级1000名学生收看比赛的情况用随机抽样方式进行调查,样本容量为50,将数据分组整理后,列表如下:
观看场数 0 1 2 3 4 5 6 7
观看人数占调查人数的百分比 8% 10% 20% 26% 12% 6% 2%
从表中可以得出正确的结论为( )
A.表中m的数值为8
B.估计观看比赛场数的中位数为3
C.估计观看比赛场数的众数为2
D.估计观看比赛不低于4场的学生约为720人
9.(2022高一下·吉林期中)关于统计数据的分析,有以下几个结论:①一组数不可能有两个众数;②将一组数据中的每个数据都减去同一个数后,方差发生变化;③调查剧院中观众的观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层抽样;④一组数据的方差一定是正数;⑤如图所示是随机抽取的200辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在[50,60]的汽车大约是60辆.
则这五种说法中错误的个数是( )
A.1 B.3 C.4 D.5
10.(2021高二上·丰台期末)抛掷一枚质地均匀的硬币,设事件“正面向上”,则下列说法正确的是( )
A.抛掷硬币10次,事件A必发生5次
B.抛掷硬币100次,事件A不可能发生50次
C.抛掷硬币1000次,事件A发生的频率一定等于0.5
D.随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小
11.某学校为了解学生对乒乓球、羽毛球运动的喜爱程度,用按比例分配的分层随机抽样法从高一、高二、高三年级所有学生中抽取部分学生做抽样调查,已知该学校高一、高二、高三年级学生人数的比例如图所示,若抽取的样本中高三年级的学生有45人,则样本容量为( )
A.125 B.100 C.150 D.120
12.(2023高三上·开远月考)某学校共有980名学生,其中高一的学生有400名,高二的学生有300名,其余都是高三的学生,为了解该校学生的体育锻炼时间,按照高一 高二 高三三个级段进行分层抽样,如果样本容量为196,那么应在高三的学生中抽取( )
A.48名 B.52名 C.56名 D.60名
13.“五月榴花妖艳烘,绿杨带雨垂垂重,五色新丝缠角粽”,这是欧阳修在《渔家傲·五月榴花妖艳烘》中描写端午节的诗句.某商家为迎接端午节,计划将粽子以“粽情粽意”礼盒形式进行销售,现利用分层随机抽样从72个蛋糕肉粽、18个碱水粽、36个豆沙粽、54个莲子粽中随机抽取10个粽子放入一个礼盒中作为展开进行试销售,则该礼盒中莲子粽的个数为( )
A.2 B.1 C.4 D.3
14.(2023高一下·湖南期末)某学校高一年级、高二年级、高三年级分别有学生800人、950人、1050人,学校为了调研学情,用分层抽样的方法从中抽取56人,则高三年级应该抽取的人数为( )
A.21 B.19 C.16 D.18
15.(2023高一下·河北期末)某学校为了解学生参加体育运动的情况,用比例分配的分层随机抽样作抽样调查,拟从初中部和高中部两层共抽取名学生,已知该校初中部和高中部分别有和名学生,则正确的( )
A.高中部产生个样本
B.初中部产生个样本
C.不同级部每个学生被抽取的可能性不相同
D.可以从两个级部各抽取个样本
16.(2023高一下·联合期末)唐代以来,牡丹之盛,以“洛阳牡丹甲天下”的美名流传于世.唐朝诗人白居易“花开花落二十日,一城之人皆若狂”和刘禹锡“唯有牡丹真国色,花开时节动京城”的诗句正是描写洛阳城的景象.已知根据花瓣类型可将牡丹分为单瓣类、重瓣类、千瓣类三类,现有牡丹花n朵,千瓣类比单瓣类多30朵,采用分层抽样方法从中选出12朵牡丹进行观察研究,其中单瓣类有4朵,重瓣类有2朵,千瓣类有6朵,则n=( )
A.360 B.270 C.240 D.180
17.(2023·玉林模拟)为了发展学生的兴趣和个性特长,培养全面发展的人才.某学校在不加重学生负担的前提下.提供个性、全面的选修课程.为了解学生对于选修课《学生领导力的开发》的选择意愿情况,对部分高二学生进行了抽样调查,制作出如图所示的两个等高条形图,根据条形图,下列结论正确的是( )
A.样本中不愿意选该门课的人数较多
B.样本中男生人数多于女生人数
C.样本中女生人数多于男生人数
D.该等高条形图无法确定样本中男生人数是否多于女生人数
18.(2023·绵阳模拟)据统计,我国牛、羊肉集贸市场价格在2019年波动幅度较大,2020年开始逐渐趋于稳定.如下图分别为2019年1月至2020年3月,我国牛肉、羊肉集贸市场月平均价格大致走势图,下列说法不正确的是( )
A.2019年1月至2020年3月,牛肉与羊肉月平均价格的涨跌情况基本一致
B.2019年3月开始至当年末,牛肉与羊肉的月平均价格都一直持续上涨
C.2019年7月至10月牛肉月平均价格的平均增量高于2020年1至2月的增量
D.同期相比,羊肉的月平均价格一定高于牛肉的月平均价格
19.(2023·南宁模拟)某商场一年中各月份的收入、支出情况的统计如图所示,则下列说法中不正确的是( )
A.支出最高值与支出最低值的比是6:1
B.利润最高的月份是2月份
C.第三季度平均收入为50万元
D.1~2月份的支出的变化率与10~11月份的支出的变化率相同
20.(2023·宜宾模拟)2月国家统计局发布中华人民共和国2022年国民经济和社会发展统计公报.下图1是2018-2022年国内生产总值及其增长速度,图2是2018-2022年三次产业增加值占国内生产总值比重(三次产业包括第一产业,第二产业,第三产业).根据图1,图2,以下描述不正确的是( )
A.2018-2022年国内生产总值呈逐年增长的趋势
B.2020年与2022年国内生产总值的增长速度较上一年有明显回落
C.2018-2022年第三产业增加值占国内生产总值比重的极差为1.7%
D.2020年第二产业增加值较2019年有所减少
21.(2023·广东模拟)如图所示是中国2012-2021年汽车进 出口量统计图,则下列结论错误的是( )
A.2012-2021年中国汽车进口量和出口量都是有增有减的
B.从2018年开始,中国汽车的出口量大于进口量
C.2012-2021年中国汽车出口量的第60百分位数是106万辆
D.2012-2021年中国汽车进口量的方差大于出口量的方差
22.(2023·江苏会考)党的二十大报告指出:“全面提高人才自主培养质量,着力造就拔尖创新人才,聚天下英才而用之.”某区域教育部门为提高学生的创新能力,组织了200名学生参与研究性学习,每人仅参加1个课题组,参加各课题组的人数占比的扇形统计图如图所示,则参加数学类的人数比参加理化类的人数多( )
A.16 B.30 C.32 D.62
23.(2023高二上·朝阳开学考)某市6月前10天的空气质量指数为35,54,80,86,72,85,58,125,111,53,则这组数据的第70百分位数是( )
A.86 B.85.5 C.85 D.84.5
24.某校为了解本校高三学生学习心里状态,采用系统抽样方法从80人中抽取40人参加某种测试,为此将题目随机编号1,2,,800,分组后在第一组采用简单随机抽样的方法抽到号码为18,抽到的40人中,编号落入区间的人做试卷,编号落入区间的人做试卷,其余的人做试卷,则做试卷的人数为( )
A.10 B.12 C.18 D.28
25.(2023高二上·柳州开学考)某新闻机构想了解全国人民对《长津湖之水门桥》的评价,决定从某市3个区按人口数用分层抽样的方法抽取一个样本,若3个区人口数之比为2:3:4,且人口最少的一个区抽出100人,则这个样本的容量为( )
A.550 B.500 C.450 D.400
26.(2023高二上·昆明开学考)某学校随机抽取了部分学生,对他们每周使用手机的时间进行统计,得到如下的频率分布直方图.则下列说法:①;②若抽取100人,则平均用时13.75小时:③若从每周使用时间在,三组内的学生中用分层抽样的方法选取8人进行访谈,则应从使用时间在内的学生中选取的人数为3.其中正确的序号是( )
A.①② B.①③ C.②③ D.①②③
二、多项选择题
27.一组数据:,,,,,,,则( )
A.这组数据的平均数为 B.这组数据的方差为
C.这组数据的极差为 D.这组数据的第百分位数为
三、填空题
28.(2023高一下·湖州期末)已知采用分层抽样得到的高三男生、女生各100名学生的身高情况为:男生样本平均数为172cm,方差为120,女生样本平均数165cm,方差为120,则总体样本方差是 .
29.数据,,的方差为,则数据,,的平均数为 .
30.下列叙述中正确的是 .(填写所有正确命题的序号)
①随机从某校高一600名男生中抽取60名学生调查身高,该调查中样本量是60
②数据2,3,3,5,9,9的中位数为3和5,众数为3和9
③数据9,10,11,11,16,20,22,23的75%分位数为21
④若将一组数据中的每个数都加上2,则平均数和方差都没有发生变化
答案解析部分
1.【答案】C
【解析】【解答】 ①社区中各个家庭收入差别明显,应该用分层随机抽样法;②由于样本量不大,且抽取的人数较少,故采用简单随机抽样法.
故选: C.
【分析】 根据分层抽样,简单随机抽样的定义进行判断,即可得答案.
2.【答案】D
【解析】【解答】用随机数表法选取样本时,样本的编号位数要一致,
故总体容量为108,用随机数表法抽取一个容量为10的样本,对总体的编号为001,002,…,108
故答案为:D
【分析】利用已知条件结合随机数表法,进而得出对总体的编号正确的选项。
3.【答案】A
【解析】【解答】解:根据题意,用随机数表抽取的样本为42、14、20、32,
则第四个编号为32;
故答案为:A
【分析】根据随机数表法的读取方法,依次读取,即可求解出答案.
4.【答案】C
【解析】【解答】抽取的样本容量为,A正确,不符合题意;
该校学生中对兴趣爱好类课程满意的人数约为,B正确,不符合题意;
根据题意,创新素质类课程的满意率为,,C错误,符合题意;
该校学生中选择学科拓展类课程的人数为,D正确,不符合题意.
故答案为:C.
【分析】根据学校人数和抽样比例即可求出样本容量,根据学校总人数结构统计图逐一判断即可.
5.【答案】B
【解析】【解答】解:因为所研究的总体中差异很大,为了让样本具有代表性,最合理的抽样方法是分层抽样.
故答案为:B.
【分析】 根据所研究的对象差异性很大,要使样本具有代表性,最合理的抽样方法是分层抽样.
6.【答案】C
【解析】【解答】对于A,不同年级的学生身体发育情况差别较大,适合用分层抽样,A不是;
对于B,总体容量较大,并且各村庄人口、地域、发展等方面的差异,不宜用简单随机抽样,B不是;
对于C,总体容量较小,个体之间无明显差异,适宜用简单随机抽样;
对于D,总体容量较大,不同年龄的人癌症的发病情况不同,不宜用简单随机抽样,D不是.
故答案为:C
【分析】利用已知条件结合简单随机抽样的方法,进而找出正确的答案。
7.【答案】B
【解析】【解答】应从女性居民中抽取的人数为
故答案为:B
【分析】根据分层抽样按比例抽取计算可得答案.
8.【答案】B
【解析】【解答】对A,由频率分布表的性质,得:m=100﹣8﹣10﹣20﹣26﹣12﹣6﹣2=16,故A错误;
对B,因为,,故中位数为3,故B正确;
对C,因为观看场数为3占的比例最高,故观看比赛场数的众数为3;
对D,观看比赛不低于4场的学生所占比率为:16%+12%+6%+2%=36%,
∴估计观看比赛不低于4场的学生约为:1000×36%=360人,故D错误;
故答案为:B.
【分析】由随机抽样的调查结果,结合图表的性质以及中位数和众数公式代入数值计算出结果即可。
9.【答案】C
【解析】【解答】解:对于①,若一组数据中有多个不同的数出现的次数相同且均出现次数最多,则几个数均为该组数据的众数,①错误;
对于②,将一组数据中每个数据都减去同一个数后,平均数也减去同一个数,则方差不变,②错误;
对于③,从50排(每排人数相同)中任意抽取一排的人进行调查,每排被抽到的概率均相同,属于简单随机抽样,③错误;
对于④,若一组数据都是完全相等的数,则该组数据方差为0,④错误;
对于⑤,由频率分布直方图可知:时速在[50,60]的频率为0.03×10=0.3,则时速在[50,60]的汽车大约有200×0.3=60辆,⑤正确.
故选:C.
【分析】由众数定义、方差的性质、抽样方法和频率分布直方图计算频数的方法依次判断各个选项即可.
10.【答案】D
【解析】【解答】不管抛掷硬币多少次,事件A发生的次数是随机事件,ABC不符合题意;
随着抛掷硬币次数的增多,事件A发生的频率在0.5附近波动的幅度较大的可能性小;
故答案为:D
【分析】根据已知条件,结合随机事件的概率及及性质逐项进行分析,可得答案。
11.【答案】A
【解析】【解答】解:由扇形统计图可知,高三年级的学生占总人数的36%,而抽取的样本中高三年级的学生人数为45人,所以样本容量为人.
故答案为:A.
【分析】根据分层抽样中,抽样比相同根据抽取的样本中高三年级的人数即可求得样本容量.
12.【答案】C
【解析】【解答】解:高三的学生有, 应在高三的学生中抽取名.
故答案为:C.
【分析】根据分层抽样分析运算即可.
13.【答案】D
【解析】【解答】解:依题意得,莲子粽在礼盒中的比例为,
则该礼盒中莲子粽的个数为.
故答案为:D.
【分析】根据分层抽样定义可得莲子粽在礼盒中的比例,从而可计算个数得出结论.
14.【答案】A
【解析】【解答】解:高三年级应该抽取的人数为.
故答案为:A.
【分析】根据分层抽样的性质列式计算求解.
15.【答案】A
【解析】【解答】解:根据已知条件,易知分层抽样的抽样比为,故该校初中部产生的样本容量为,高中部产生的样本容量为.
故答案为:A.
【分析】先利用分层抽样确定抽样比,再分别计算各部产生的样本容量即可.
16.【答案】D
【解析】【解答】设 单瓣类 有朵,则 千瓣类 有朵,
由题意可得,解得,
即单瓣类 有60朵,则 千瓣类 有90朵,
则,解得.
胡答案为:D.
【分析】根据题意结合分层抽样的抽样比不变列式求解.
17.【答案】B
【解析】【解答】对于A,由图乙可知,样本中男生,女生都大部分愿意选择该门课,
则样本中愿意选该门课的人数较多,A不符合题意;
对于BCD,由图甲可知,在愿意和不愿意的人中,都是男生占比较大,
所以可以确定,样本中男生人数多于女生人数,B符合题意,CD不符合题意.
故答案为:B.
【分析】根据等高条形图直接判断各个选项即可.
18.【答案】D
【解析】【解答】根据图像的大致走势即可判断牛肉与羊肉月平均价格的涨跌情况基本一致,A正确,不符合题意;
根据图像中的数据比较可知2019年3月开始至当年末,牛肉与羊肉的月平均价格,数据越来越大,都一直持续上涨,B正确,不符合题意;
2019年7月至10月牛肉月平均价格的平均增量为,2020年1至2月牛肉增量为,C正确,不符合题意;
2019年8月牛肉月平均价格为,2019年8月羊肉月平均价格为,所以同期相比,羊肉的月平均价格也可能会低于牛肉的月平均价格,D错误,符合题意.
故答案为:D.
【分析】根据图像数据分析即可求解.
19.【答案】B
【解析】【解答】支出最高值为60万元,支出最低值为10万元,支出最高值与支出最低值的比是,A正确,不符合题意;
2月份利润为20万元,3月份和10月份利润为30万元,利润最高的月份是3月份和10月份,B错误,符合题意;
7,8,9月份收入分别为40万元,50万元,60万元,则第三季度平均收入为50万元,C正确,不符合题意;
1~2月份的支出变化率为 ,10~11月份的支出变化率为 ,故变化率相同,D正确,不符合题意.
故答案为:B
【分析】由统计图中数据,对选项中的统计结论进行判断.
20.【答案】D
【解析】【解答】依题意,
对于A:由图1可以看出直方图逐年增高,所以2018-2022年国内生产总值呈逐年增长的趋势,A符合题意;
对于B:由图1可以看出折线在2020年与2022年时与上一年连线的斜率小于0,B符合题意;
对于C:由图2可以得出2018-2022年第三产业增加值占国内生产总值比重最大值为:54.5%,
最小值为:52.8%,所以极差,C符合题意;
对于D:结合图1图2可知,2019年第二产业的增加值为:亿元;
2020年第二产业的增加值为:亿元.
因为,所以2020年第二产业增加值较2019年有所增加,
D不符合题意.
故答案为:D.
【分析】根据给出的图形逐一分析判断即可.
21.【答案】D
【解析】【解答】由条形图可知2012-2021年中国汽车进口量和出口量都是有增有减的,所以A正确,不符合题意;
由条形图可知从2018年开始,中国汽车的出口量大于进口量,所以B正确,不符合题意;
2012-2021年中国汽车出口量由小到大排列为:,因此第60百分位数是,所以C正确,不符合题意;
由条形图可知2012-2021年中国汽车进口量的波动小于出口量的波动,因此2012-2021年中国汽车进口量的方差小于出口量的方差,所以D错误,符合题意,
故答案为:D
【分析】根据条形图,结合百分位数、方差的性质逐一判断即可.
22.【答案】C
【解析】【解答】由扇形统计图可知参加数学类的人数为,
参加理化类的人数为,
故参加数学类的人数比参加理化类的人数多,
故答案为:C
【分析】由扇形图计算参加数学类和理化类的人数,即可求得答案.
23.【答案】B
【解析】【解答】解:将这组数据从小到大排序为: 35,53,54,58,72,80,85,86,111,125,又,这组数据的第70百分位数是.
故答案为:B.
【分析】先将这组数据从小到大排列,再根据百分位数定义求解.
24.【答案】B
【解析】【解答】 ,
间隔为20.
故做试卷 与 的人数共为 ,
做问卷 的人数为 ,
故答案为:B.
【分析】利用已知条件结合系统抽样的方法,进而得出做试卷的人数。
25.【答案】C
【解析】【解答】解:设这个样本的容量为,则,求得.
故答案为:C.
【分析】根据分层抽样原理计算求解.
26.【答案】D
【解析】【解答】解:,求得, ①正确;
根据频率分布直方图计算估计出每周人使用手机时间为,②正确;
每周使用时间在,三组内的学生的比例为,根据分层样原理得选取8人进行访谈, 则应从使用时间在内的学生中选取的人数为3,③ 正确.
故答案为:D.
【分析】 ① 根据频率分布直方图中小矩形的面积和为1, ② 求出频率分布直方图的平均值,即为抽取100人的平均值的估计值, ③ 利用分层抽样计算出使用时间在 内的学生中选取的人数.
27.【答案】A,D
【解析】【解答】解:A、这组数据的平均数为:,A正确;
B、这组数据的方差为:,B错误;
C、这组数据的极差为:,C错误;
D、,第70百分位数是第5个数7,D正确.
故答案为:AD.
【分析】利用公式分别计算平均数、方差、极差、第70百分位数判断选项.
28.【答案】132.25
【解析】【解答】设总体平均数为,方差为,男生平均数为,方差为,女生平均数为,方差为,由题意得,,,,
故答案为:132.25
【分析】根据分层抽样原理,代入平均数和方差公式进行求解。
29.【答案】:7或
【解析】【解答】解:因为 方差为,解得,
所以数据,,的平均数为或.
故答案为:7或.
【分析】根据题意结合方差公式可得,结合平均数的性质运算求解.
30.【答案】①③
【解析】【解答】解:对于 ① : 随机从某校高一600名男生中抽取60名学生调查身高,该调查中样本量是60 ,故①正确;
对于② :中位数为, 众数为3和9 ,故②错误;
对于③ :因为,所以 75%分位数为 第6位数和第7位数的平均数,故 ③ 错误;
对于 ④ : 若将一组数据中的每个数都加上2, 则 平均数 加2,方差为原来的4倍,故 ④ 错误;
故答案为: ①③ .
【分析】对①:根据样本容量的概念分析判断;对② :根据中位数、众数的概念分析判断;对 ③ :根据百分位数的概念分析判断;对 ④ :根据平均数、方差的性质分析判断.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
