高中数学人教A版(2019)必修2 9.2 用样本估计总体 解答题专项章节综合练习题(答案+解析)
文档属性
| 名称 | 高中数学人教A版(2019)必修2 9.2 用样本估计总体 解答题专项章节综合练习题(答案+解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-31 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
9.2 用样本估计总体 解答题专项
一、解答题
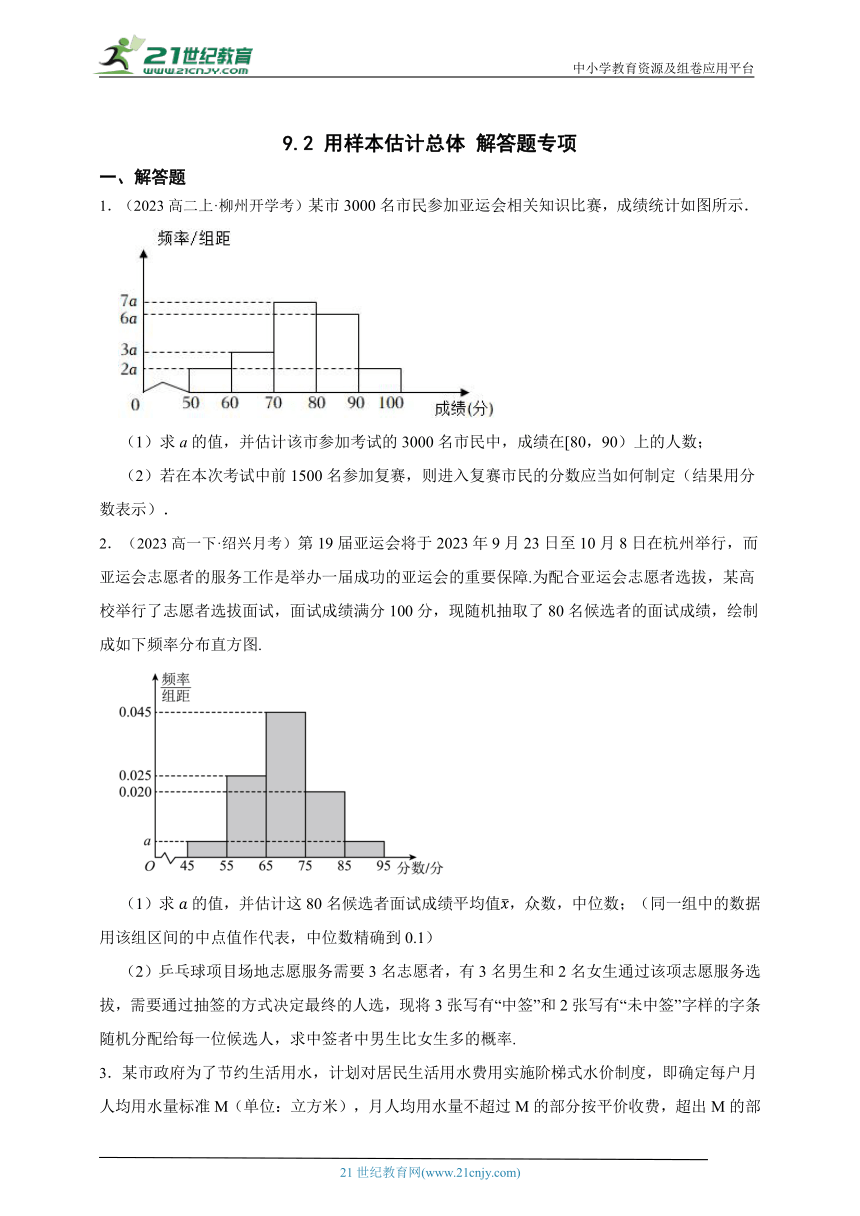
1.(2023高二上·柳州开学考)某市3000名市民参加亚运会相关知识比赛,成绩统计如图所示.
(1)求a的值,并估计该市参加考试的3000名市民中,成绩在[80,90)上的人数;
(2)若在本次考试中前1500名参加复赛,则进入复赛市民的分数应当如何制定(结果用分数表示).
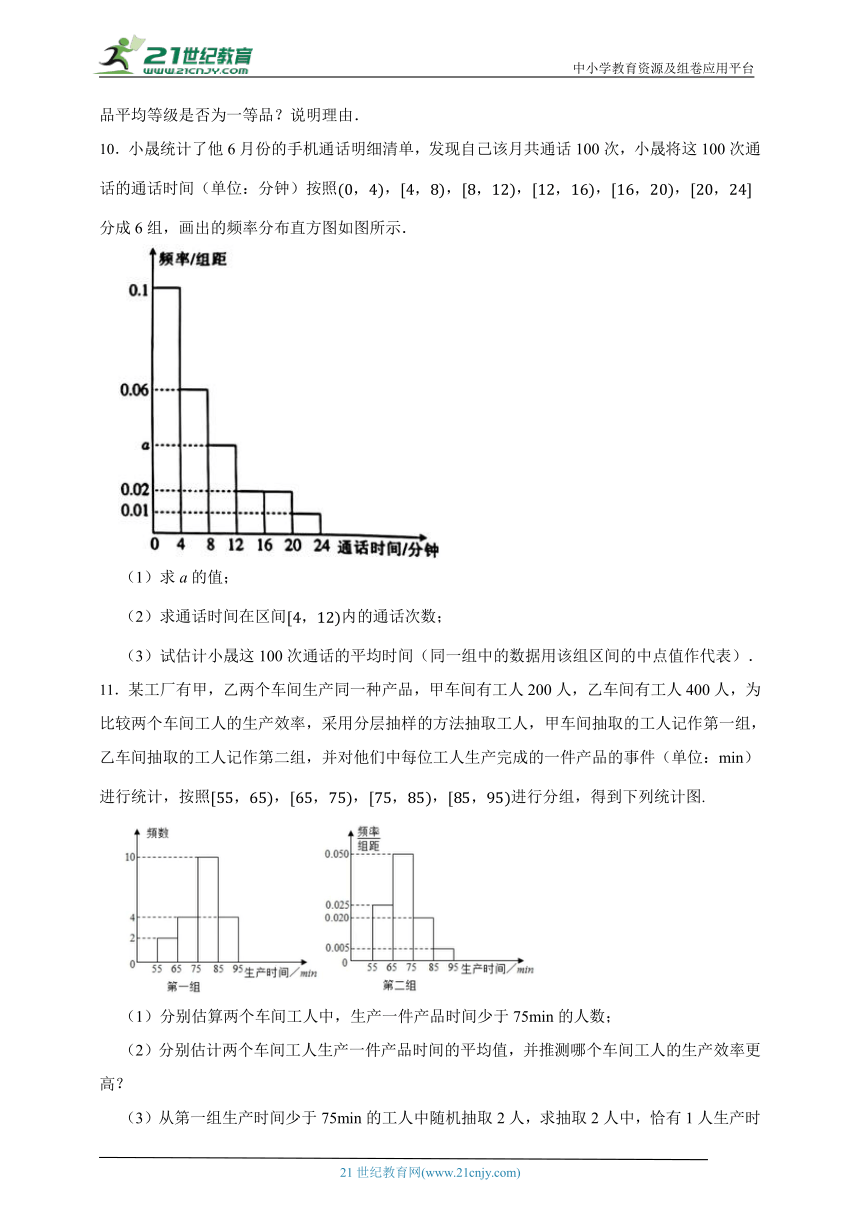
2.(2023高一下·绍兴月考)第19届亚运会将于2023年9月23日至10月8日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障.为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分100分,现随机抽取了80名候选者的面试成绩,绘制成如下频率分布直方图.
(1)求的值,并估计这80名候选者面试成绩平均值,众数,中位数;(同一组中的数据用该组区间的中点值作代表,中位数精确到0.1)
(2)乒乓球项目场地志愿服务需要3名志愿者,有3名男生和2名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将3张写有“中签”和2张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
3.某市政府为了节约生活用水,计划对居民生活用水费用实施阶梯式水价制度,即确定每户月人均用水量标准M(单位:立方米),月人均用水量不超过M的部分按平价收费,超出M的部分按议价收费.现随机抽取200户进行调查,抽取的用户月人均用水量的频率分布直方图如图所示.
(1)求频率分布直方图中的值;
(2)如果希望的用户月人均用水量不超过标准M,那么标准M定为多少比较合理?
(3)若从月人均用水量在,,三组的用户中采用按比例分层抽样的方法选取6户参加节水座谈会,再从6户中随机地抽2户发言,求发言的2户来自不同组的概率.
4.(2023高一下·余姚期末)某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
5.(2023高二下·绍兴期末)中国电动汽车重大科技项目的研发开始于2001年,经过一系列的科技攻关以及奥运、世博、“十城千辆”示范平台等应用拉动,中国电动汽车建立起了具有自主知识产权的全产业链技术体系.汽车工业协会的最新数据显示,2022年中国电动汽车销量达491万辆,是2010年的400多倍.某人打算购买一款国产电动汽车,调查了100辆该款车的续航里程,得到频率分布表如下:
续航里程(单位:km) 频数 频率
3 0.03
10 0.10
30 0.30
35 0.35
15 0.15
7 0.07
(1)在图中作出频率分布直方图;
(2)根据(1)中作出的频率分布直方图估计该款车续航里程的众数与平均数.
(同一组中的数据以该组区间的中间值为代表)
6.(2023高一下·安徽月考)某果园试种了两个品种的桃树各10棵,并在桃树成熟挂果后统计了这20棵桃树的产量如下表,记两个品种各10棵产量的平均数分别为和,方差分别为和.
(单位:) 60 50 45 60 70 80 80 80 85 90
(单位:) 40 60 60 80 80 55 80 80 70 95
(1)求,,,;
(2)果园要大面积种植这两种桃树中的一种,依据以上计算结果分析选种哪个品种更合适 并说明理由.
7.(2020高一下·永寿月考)如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)求 这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格).
8.某校举行了一次高一年级数学竞赛,笔试成绩在50分以上(包括50分,满分100分)共有100人,分成[50,60)、[60,70)、[70,80)、[80,90)、[90,100]五组,得到如图所示频率分布直方图.
(1)根据频率分布直方图估计这次数学竞赛成绩的平均数和中位数(中位数精确到0.1);
(2)为进一步了解学困生的学习情况,从数学成绩低于70分的学生中,通过分层随机抽样的方法抽取6人,再从这6人中任取3人,求此3人分数都在[60,70)的概率.
9.(2023高二上·朝阳开学考)某工厂生产某款产品,该产品市场评级规定:评分在10分及以上的为一等品,低于10分的为二等品.下面是检验员从一批产品中随机抽取的10件产品的评分:
9.6 10.1 9.7 9.8 10.0 9.7 10.0 9.8 10.1 10.2
经计算得,其中为抽取的第i件产品的评分,.
(1)求这组样本平均数和方差;
(2)若厂家改进生产线,使得生产出的每件产品评分均提高0.2.根据以上随机抽取的10件产品改进后的评分,估计改进后该厂生产的产品评分的平均数和方差;
(3)在第(2)问前提下,再从改进后生产的产品中随机抽取的10件产品,估计这10件产品平均等级是否为一等品?说明理由.
10.小晟统计了他6月份的手机通话明细清单,发现自己该月共通话100次,小晟将这100次通话的通话时间(单位:分钟)按照,,,,,分成6组,画出的频率分布直方图如图所示.
(1)求a的值;
(2)求通话时间在区间内的通话次数;
(3)试估计小晟这100次通话的平均时间(同一组中的数据用该组区间的中点值作代表).
11.某工厂有甲,乙两个车间生产同一种产品,甲车间有工人200人,乙车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:min)进行统计,按照,,,进行分组,得到下列统计图.
(1)分别估算两个车间工人中,生产一件产品时间少于75min的人数;
(2)分别估计两个车间工人生产一件产品时间的平均值,并推测哪个车间工人的生产效率更高?
(3)从第一组生产时间少于75min的工人中随机抽取2人,求抽取2人中,恰有1人生产时间少于65min的概率.
12.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值,将该指标大于的人判定为阳性,小于或等于的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布.
(1)当漏诊率时,求临界值和误诊率;
(2)已知一次调查抽取的未患病者样本容量为100,且该项医学指标检查完全符合上面频率分布直方图(图2),临界值,从样本中该医学指标在上的未患病者中随机抽取2人,则2人中恰有一人为被误诊者的概率是多少?
13.为了解某市家庭用电量的情况,统计部门随机调查了200户居民去年一年的月均用电量(单位:),将全部数据按区间分成8组,得到如下的频率分布直方图:
(1)求图中a的值;并估计这200户居民月用电量的平均值(同一组中的数据用该组区间的中点值为代表);
(2)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定各档月均用电量的范围(计算百分位数时,结果四舍五入取整数).
14.俄罗斯与乌克兰的军事冲突导致石油、天然气价格飙升.燃油价格问题是人们关心的热点问题,某网站为此进行了调查.现从参与者中随机选出100人作为样本,并将这100人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示
(1)求样本中数据落在的频率;
(2)求样本数据的第60百分位数;
(3)若将频率视为概率,现在要从和两组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行座谈,求抽取的2人中至少有1人的年龄在这一组的概率.
15.(2023高二上·梅河口开学考)为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求该班学生周末的学习时间不少于小时的人数;
(2)估计这名同学周末学习时间的分位数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
16.(2023高一下·台州期末)第19届亚运会将于2023年9月23日至10月8日在杭州举行,为了弘扬奥林匹克和亚运精神,某学校对全体高中学生组织了一次关于亚运会相关知识的测试.从全校学生中随机抽取了100名学生的成绩作为样本进行统计,测试满分为100分,并将这100名同学的测试成绩分成5组,绘制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值,并估计这100名学生的平均成绩;
(2)用样本频率估计总体,如果将频率视为概率,从全校学生中随机抽取3名学生,求3名学生中至少有2人成绩不低于80分的概率.
17.(2023高一下·马鞍山期末)某小学对在校学生开展防震减灾教育,进行一段时间的展板学习和网络学习后,学校对全校学生进行问卷测试(满分分).现随机抽取了部分学生的答卷,得分的频数统计表和对应的频率分布直方图如图所示:
得分
人数
(1)求,的值,并估计全校学生得分的平均数;
(2)根据频率分布直方图,估计样本数据的和分位数.
18.(2023高二下·嘉定期末)某校高二年级一个班有60名学生,将期中考试的数学成绩(均为整数)分成六段:,得到如图所示的频率分布直方图,
(1)求的值;
(2)用分层随机抽样的方法从中抽取一个容量为20的样本,已知甲同学的成绩在,乙同学的成绩在,求甲乙至少一人被抽到的概率.
19.(2023高二下·杨浦期末) 某校高二年级共有学生200人,其中男生120人,女生80人.为了了解全年级学生上学花费时间(分)的信息,按照分层抽样的原则抽取了样本,样本容量为20,并根据样本数据信息绘制了茎叶图和频率分布直方图.由于保存不当,茎叶图中有一个数据不小心被污染看不清了(如图),频率分布直方图纵轴上的数据也遗失了.
(1)根据茎叶图提供的有限信息,求频率分布直方图中和的值,指出样本的“中位数、平均数、众数、方差、极差”中,哪些已经能确定,并计算它们的值;
(2)通过对样本原始数据的计算,得到男生上学花费时间的样本均值为30(分),女生的样本均值为27.75(分),试计算被污染的数值,并根据样本估计该年级全体学生上学花费时间的“中位数、平均数、方差”.
20.(2023高二下·成都期末)现在的高一年级学生将会是四川省首届参加新高考的学生,高考招生计划按历史科目组合与物理科目组合分别编制.为了了解某校高一学生的物理学习情况,在一次全年级物理测试后随机抽取了100名学生的物理成绩,将成绩分为,,,,,共6组,得到如图所示的频率分布直方图,记分数低于60分为不及格.
(1)求直方图中a的值,并估计本次物理测试的及格率;
(2)在样本中,采取分层抽样的方法从成绩不及格的学生中抽取6名作试卷分析,再从这6名学生中随机抽取2名做面对面交流,求2名面对面交流学生的成绩均来自的概率.
21.(2023高一下·衢州期末)随着现代社会物质生活水平的提高,中学生的零花钱越来越多,消费水平也越来越高,因此滋生了一些不良的攀比现象.某学校为帮助学生培养正确的消费观念,对该校学生每周零花钱的数额进行了随机调查,现将统计数据按,,…,分组后绘成如图所示的频率分布直方图,已知.
(1)求频率分布直方图中,的值;
(2)估计该校学生每周零花钱的第55百分位数;
(3)若按照各组频率的比例采用分层随机抽样的方法从每周零花钱在内的人中抽取11人,求内抽取的人数.
22.某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照 , , , 分成9组,制成样本的频率分布直方图如图所示.
(1) 求图中 的值;
(2) 估计该校高一学生周末“阅读时间”的中位数;
(3) 在 , 这两组中采用分层抽样抽取7人,再从7人中随机抽取2人,求抽取的两人恰好都在一组的概率.
23.(2023高二下·玉林期中)全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
24.(2023高一下·安徽竞赛)某学校需要从甲、乙两名学生中选一人参加全国高中数学竞赛,现整理了近期两人5次模拟考试的成绩,结果如下表:
第一次 第二次 第三次 第四次 第五次
甲的成绩(分) 78 80 65 85 92
乙的成绩(分) 75 86 70 95 74
(1)如果根据甲、乙两人近5次的考试成绩,你认为选谁参加较合适?并说明理由;
(2)如果按照如下方案推荐参加全国高中数学竞赛:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加全国高中数学竞赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加全国高中数学竞赛,否则被淘汰.
已知学生甲只会5道备选题中的3道,那么学生甲选择哪种答题方案可参加全国高中数学竞赛的可能性更大?并说明理由.
25.(2023高二下·普宁月考)某大学为调研学生在,两家餐厅用餐的满意度,从在,两家餐厅都用过餐的学生中各随机抽取了200人,每人分别对这两家餐厅进行评分,满分为60分.整理评分数据,将分数分成6组:,,,,,,得到餐厅分数的频率分布直方图和餐厅分数的频数分布表:
餐厅分数的频数分布表:
分数区间 频数
4
6
10
30
80
70
定义学生对餐厅评价的“满意度指数”如下:
分数
满意度指数 3 4 5
(1)在抽样的200人中,求对餐厅评价“满意度指数”为4的人数;
(2)从该校在,两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率;
(3)如果从,两家餐厅中选择一家用餐,从期望的角度你会选择哪一家?并说明理由.
26.(2023·黄山模拟)为了深入学习领会党的二十大精神,某高级中学全体学生参加了《二十大知识竞赛》,试卷满分为100分,所有学生成绩均在区间分内,已知该校高一 高二 高三年级的学生人数分别为800 1000 1200现用分层抽样的方法抽取了300名学生的答题成绩,绘制了如下样本频率分布直方图.
年级 样本平均数 样本方差
高一 60 75
高二 63
高三 55
(1)根据样本频率分布直方图估计该校全体学生成绩的众数 平均数 第71百分位数;
(2)已知所抽取各年级答题成绩的平均数 方差的数据如下表,且根据频率分布直方图估计出总成绩的方差为140,求高三年级学生成绩的平均数,和高二年级学生成绩的方差.
27.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,现从参与调查的人群中随机选出20人的样本,并将这20人按年龄分组:第1组 ,第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直方图如图所示
(1)求a的值.
(2)根据频率分布直方图,估计参与调查人群的样本数据的 分位数(保留两位小数).
(3)若从年龄在 的人中随机抽取两位,求两人恰有一人的年龄在 内的概率.
28.随着移动互联网的发展,与餐饮美食相关的手机 软件层出不穷,现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:
(1)使用A订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及中位数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
29.(2020高一下·安徽月考)某校为了解高一1000名学生的物理成绩,随机抽查部分学生期中考试的成绩,将数据分成 , , , 4组,绘制成如图所示的频率分布直方图.
(1)求a的值;
(2)根据频率分布直方图,估计这次物理成绩的平均分(用组中值代替各组数据的平均值);
(3)若在本次考试中,规定物理成绩比平均分高15分以上的为优秀,估计该校学生物理成绩的优秀率(用百分数表示).
30.(2023高二上·柳州开学考)某种零件按质量标准分为1,2,3,4,5五个等级.现从一批该零件中随机抽取40个,对其等级进行统计分析,得到频率分布表如表:
等级 1 2 3 4 5
频率 0.05 m 0.15 0.35 n
(1)若抽取等级为5的零件的概率为0.1,求m,n;
(2)在(1)的条件下,从等级为1和5的所有零件中任意抽取2个,求抽取的2个零件等级恰好相同的概率.
答案解析部分
1.【答案】(1)解:由已知得:(2a+2a+3a+6a+7a)×10=1得:a=0.005,
故成绩在[80,90)上的频率为0.03×10=0.3,
故成绩在[80,90)上的人数为:3000×0.3=900(人);
(2)解:设50%分位数为x,则(2×0.005+3×0.005)×10+7×0.05××10=0.5,
解得x=(分),故进入复赛市民的分数应当不低于分.
【解析】【分析】(1)根据所以小长方形的面积和为1求解a,再求得成绩在[80,90)的频率,根据频数计算公式 人数;
(2)结合已知数据根据频率分布直方图求50%分位数即可.
2.【答案】(1)解:由频率分布直方图可知,解得,
,
众数为70,
因为前2组的频率和为,前3组的频率和为,
所以中位数在第3组,设中位数为,则
,解得,
所以中位数为.
(2)解:记3名男生分别为,记2名女生分别为,则所有抽签的情况有:
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签,共有10种情况,
其中中签者中男生比女生多的有:未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签,共7种,
所以中签者中男生比女生多的概率为.
【解析】【分析】(1)首先根据频率和为1可列出关于a的方程并解出a的值,其次根据平均数、众数的定义即可求出平均数、众数,求中位数需要先判断中位数的位置,再列方程求解;
(2)首先利用列举法列出所有抽签的情况,可知其中中签者中男生比女生多的共有7种,即可计算概率.
3.【答案】(1)解:因为图中所有矩形面积之和为1,
所以,
解得.
(2)解:由图象可知,月人均用水量低于2立方米的居民占比为
,
月人均用水量低于立方米的居民占比为
,
根据分位数的含义可知,,
且,解得.
(3)解:由图象可知,内的频率为,内的频率为,内的频率为,
所以,根据分层抽样知,应从中抽3户,记作,中抽2户,记作,中抽1户,记作.
则从这6户中抽取2户有,,,,,,,,,,,,,,,共包含个等可能的样本点,
满足发言的2户来自不同组的有,,,,,,,,,,共包含个样本点,
根据古典概型可知,发言的2户来自不同组的概率.
【解析】【分析】 ( 1 )根据频率分布直方图中小矩形面积之和为1,列出方程,求解即可得 的值;
( 2 )利用百分位数的概念列出方程,求解即可得出M的值;
( 3 )求出3个区间内的频率,根据分层抽样得出每个区间应该抽取的人数,然后列举出所有的点,再根据古典概型概率公式,即可求出发言的2户来自不同组的概率.
4.【答案】(1)解:由题意可知,样本容量n==50,
,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030;
(2)解:设本次竞赛学生成绩的中位数为m,平均分为,
则[0.016+0.03]×10+(m﹣70)×0.040 =0.5,解得,
=(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6,
(3)解:由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,
分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种,
分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),
(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2).
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率.
【解析】【分析】本题主要考查频率分布直方图、频率与频数的关系及古典概型的计算公式等有关知识的综合运用,
(1)根据得分在,的频数分别为8和2,再结合频率分布直方图即可求出x、y的值;
(2)根据频率分布直方图中提供的数据信息求解中位数和平均分即可;
(3)运用列举法先将分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种分别列出,再将其中2名同学的分数都不在[90,100]内的情况有10种分别列出,最后利用古典概型计算公式求解即可.
5.【答案】(1)解:
(2)解:众数:275
平均数:
【解析】【分析】(1)根据频率分布表作出频率分布直方图;
(2)根据频率分布直方图最高矩形底边中点值为该款车续航里程的众数,将每个矩形底边中点值乘以对应矩形面积全部结果相加得到平均数。
6.【答案】(1)解:,
,
,
.
(2)解:由可得两个品种平均产量相等,
又,则品种产量较稳定,故选择品种.
【解析】【分析】(1)利用平均数和方差定义代入数据计算;
(2)比较 两个品种的平均产量和产量的稳定程度。
7.【答案】(1)解: 这一组的频率为 ,
这一组的频数为 ;
(2)解:估计这次环保知识竞赛的及格率( 分及以上为及格) .
【解析】【分析】(1) 根据题意由已知的频率分布图的数据即可计算出结果。
(2)由概率的定义结合题意即可得出答案。
8.【答案】(1)由,解得,
这次数学竞赛成绩的平均数为,
前2组的频率和为,前3组的频率和为,
所以中位数为.
(2)分层抽样抽取的6人中,数学成绩位于的有人,记为a,b.
数学成绩位于的有人,记为A、B、C、D,
从6人中任取3人,基本事件有:abA、abB、abC、abD、aAB、aAC、aAD、aBC、aBD、aCD,bAB、bAC,bAD,bBC、bBD,bCD,ABC,ABD、ACD、BCD,共20种,
其中3人分数都在的有ABC、ABD、ACD、BCD,共4种,
所以从6人中任取3人,分数都在的概率为.
【解析】
【分析】(1)由频率分布直方图列方程,可得, 这次数学竞赛成绩的平均数为,根据中位数的定义可求得样本的中位数;
(2)分层抽样抽取的6人中,数学成绩位于的有人,记为a,b. 数学成绩位于的有4人,记为 A、B、C、D ,列举出所有的基本事件,利用古典概型的概率公式即可求解.
9.【答案】(1)解:样本平均值
样本方差.
(2)解:估计改进后该厂生产的产品评分的平均数,
方差.
(3)解:可以认为是一等品.因为改进后该厂生产的产品评分由样本数据估计平均数为,所以可以认为这10件产品平均等级为一等品不一定是一等品.
因为样本数据具有随机性,所以新样本平均值不一定达到10分及以上,所以新样本平均等级不一定是一等品.
【解析】【分析】(1)利用平均数和方差的定义求解;
(2)根据平均数的性质和方差的性质求解;
(3)从平均数角度分析或从抽样具有随机性角度分析.
10.【答案】(1)解:由,
得.
(2)解:因为通话时间在区间内的频率为,
所以通话时间在区间内的通话次数为.
(3)解:这100次通话的平均时间的估计值为分钟.
【解析】【分析】(1)根据频率之和为1列方程求得;
(2) 通话时间在区间内的频率为, 所以通话时间在区间内的通话次数为;
(3)根据频率分布直方图求得平均数,即可得解.
11.【答案】(1)解:第一组工人20人,其中在75min内(不含75min)生产完成一件产品的有6人,
∴甲车间工人中生产一件产品时间少于75min的人数为(人),
第二组工人40人.其中在75min内(不含75min)生产完成一件产品的有
人,
∴乙车间工人中生产一件产品时间少于75min的人数为(人).
(2)解:第一组平均时间为:,
第二组平均时间为:,
∵,∴乙车间工人生产效率更高.
(3)解:由题意得,第一组生产时间少于75min的工人有6人,
其中生产时间少于65min的有2人,分别用,代表,
生产时间不少于65min的工人用,,,代表,
抽取2人基本事件空间为:
,共15个基本事件.
设事件A:恰有1人生产时间少于65min,
则.
【解析】【分析】 (1) 根据题意结合频率分布直方图分析运算;
(2) 根据题意结合平均数公式运算求解,并对比分析;
(3)根据分层抽样求各层人数,利用列举法结合古典概型分析求解.
12.【答案】(1)解:依题可知,图1第一个小矩形的面积为,所以,
所以,解得,
(2)解:由题可知,100个未患病者中,该项医学指标在中的有人,
其中被误诊者有人,
记随机抽取的2人恰有一人为被误诊者为事件A.分别用a,b,c,d,E,F表示这6人,E,F代表被误诊的2人,
样本空间,
事件,故,,
,故2人中恰有一人为被误诊者的概率是.
【解析】【分析】(1)根据漏诊率的定义利用概率为0.5%可求得,再根据误诊率的定义可求得;
(2)先求出指标在中的人数,再求出其中被误诊的人数,利用列举法,将样本空间的结果一 一列举,并找到随机抽取的2人恰有一人为被误诊者所包含的样本点的个数,结合古典概型的概率计算公式可得结果.
13.【答案】(1)解:由直方图可得,样本落在
的频率分别为
,由,解得,
则样本落在的频率分别为,所以月用电量的平均值为
(2)解:为了使的居民缴费在第一档,需要确定月用电量的分位数;
的居民缴费在第二档,还需要确定月用电量的分位数.
因为,
则使的居民缴费在第一档,月用电量的分位数位于区间内,
于是.
又,所以对应的用电量为350.
所以第一档的范围是,第二档的范围是,第三档的范围是.
【解析】【分析】 (1)根据所有小长方形的面积和为1列方程求a的值,再根据频率分布直方图计算平均值;
(2)为了使75%的居民缴费在第一档,需要确定月用电量的分位数;使20%的居民缴费在第二档
需要确定月用电量的分位数,结合百分数的计算方法求解.
14.【答案】(1)解:由频率分布直方图可知,样本中数据落在的频率为
(2)解:样本数据的第60百分位数落在第四组,且第60百分位数为
(3)解:与两组的频率之比为,现从和两组中用分层抽样的方法抽取6人,则组抽取2人,记为,,组抽取4人,记为1,2,3,4.
所有可能的情况为,,,,,,,,,,,,,,,共15种.
其中至少有1人的年龄在的情况有,,,,,,,,,共9种,故所求概率
【解析】【分析】(1)根据频率分布直方图分析运算;
(2)根据题意结合百分位数的定义分析求解;
(3) 先根据分层抽样求各层人数,再利用列举法和古典概型运算求解.
15.【答案】(1)解:由图可知,该班学生周末的学习时间不少于20小时的频率为
则名学生中周末的学习时间不少于20小时的人数为.
(2)解:学习时间在小时以下的频率为,
学习时间在小时以下的频率为,
所以分位数在,
,
则这名同学周末学习时间的分位数为.
(3)解:不合理,样本的选取只选在高一某班,不具有代表性.
【解析】【分析】(1)先根据频率分布直方图求 不少于20小时的频率 ,进而求人数;
(2)根据题意分析可得 分位数在, 结合百分位数的定义运算求解;
(3)根据随机抽样的性质分析判断.
16.【答案】(1)解:由频率分布直方图可得每组的频率依次为,
则,解得,
设平均成绩的估计值为,
则(分),
所以这100名学生的平均成绩估计值为74分.
(2)解:每个学生成绩不低于80分的概率为0.4.
3名学生中恰有2人成绩不低于80分的概率;
3名学生中恰有3人成绩不低于80分的概率;
3名学生中至少有2人成绩不低于80分的概率.
【解析】【分析】 (1) 根据频率分布直方图可得相应的频率,结合频率和为求1求t,并结合平均数公式运算求解;
(2) 根据题意用频率估计概率,进而结合独立事件概率乘法公式运算求解.
17.【答案】(1)解:由频率分布直方图可知,
得分在的频率为,
故抽取的学生答卷数为,
由,得.
所以,
得分的平均数估计值为:
.
(2)解:由图可知,内的比例为,
内的比例为,内的比例为,
内的比例为.
因此,分位数一定位于.
由,
可以估计样本数据的分位数为.
类似的,由,
可以估计样本数据的分位数为.
【解析】【分析】(1)依据频率直方图以及频率求出a、b的值,再求出全校的平均数即可.
(2)根据频率分布直方图的概念,百分位数的概念求出即可.
18.【答案】(1)解:由题意可得,
解得;
(2)解:因为总体共60名学生,样本容量为20,因此抽样比为.
其中分数段有人,分数段有人,
所以在分数段中抽取人,分数段抽取人,
设甲被抽到的事件为,乙被抽到的事件为,
则,,
则甲乙至少一人被抽到的概率为.
【解析】【分析】 (1) 根据频率和为1运算求解;
(2) 先根据分层抽样求各层人数,进而可得甲、乙被抽到的概率,结合独立事件概率乘法公式运算求解.
19.【答案】(1)解:根据直方图可以看出,组距为,的频数为1,频率为,,
的频数为,频率为,
涂抹的数不确定大小,因此不能确定中位数
众数和极差可以确定,
无论被涂抹的数字是多少,不影响众数为,
极差为
(2)解:
被污染的数值为,
样本平均数,
于是样本方差
由于涂抹的数字是,故可以确定第个数是,则中位数为
于是可估计该年级全体学生上学花费时间的中位数为,平均数为,方差为.
【解析】【分析】(1)结合茎叶图和直方图组距求出 和的值, 利用”中位数、平均数、众数、方差、极差“的定义判断其值是否可以确定,并求解 ;
(2)先根据男女平均数算出被污染的数据,利用两组数的平均值求合成后的平均值,然后由方差公式计算方差。
20.【答案】(1)解:因为,
所以,
由频率分布直方图可知,成绩不少于60分的频率为,
即及格率为.
(2)解:由分层抽样可知,成绩在,分别抽取的人数为,
不妨设成绩在的2人为,成绩在的4人为,
则任取2人的所有基本事件为,,共15个,其中2人成绩都在的有6个,
所以由古典概型知.
【解析】【分析】(1)根据频率分布直方图直接计算即可得解.
(2)由分层抽样得出成绩在两个区间的人数,列出基本事件,由古典概型求解即可.
21.【答案】(1)解:,即
又,所以,.
(2)解:前3组的频率和为,
前4组的频率和为,
∴第55百分位数位于第4组内.
∴估计第55百分位数为元.
(3)解:,,这三组的频率分别为,,,比例为,
则从内抽取的人数分别为.
【解析】【分析】(1)由频率和为1可得,结合已知条件,解方程组即可求出.
(2)利用百分位数的定义,先判断第55百分位数所在的区间,结合频率直方图即可求出.
(3)先算出各组的频数,再根据各组的比例即可求出.
22.【答案】(1)解:由题意,高一学生周末“阅读时间”在 , , , 的概率分别为 0.04,0.08,0.20,0.25,0.07,0.04,0.02,
由 ,所以
(2)解:设该校高一学生周末“阅读时间”的中位数为 小时,
因为前5组频率和为 ,前4组频率和为 ,
所以 ,
由 ,得
(3)解:在 , 这两组中的人分别有15人、20人,采用分层抽样抽取7人,分别为3人、 4人,再从7人中随机抽取2人,有 种,抽取的两人恰好都在一组,有 种,故所求概率为
【解析】【分析】(1)根据频率分布直方图中小长方形的面积之和等于1,求 的值;
(2)根据频率分布直方图设中位数为 ,然后列出方程求解;
(3)根据分层抽样原理结合古典概型的计算公式求解.
23.【答案】(1)解:根据茎叶图,得到样本中男职工健康指数的众数是,
中位数是;
(2)解:根据茎叶图,按男女用分层抽样从这名职工中随机抽取人,
抽样比
男职工抽(人),记为,女职工人,记为,
从这人中随机抽取人,所有的基本事件是、、、、、
、、、、共种,
抽取的人都是男职工的事件为、、,
故所求的概率为P;
(3)解:由题意知: ,解得;
所以样本中所有女职工的健康指数平均数为,
方差为.
【解析】【分析】(1)根据茎叶图中的数据,计算样本中男职工健康指数的众数和中位数;
(2)根据分层抽样的基本原理可以求出男,女职工人数,用列举法求出基本事件数,计算所求的概率值;
(3)根据题意求出x的值,再计算健康指数的平均数和方差.
24.【答案】(1)解:选派甲参加数学竞赛较合适.
由题意得,
,
,
,
由,可知甲、乙的平均分相同,但甲的成绩比乙稳定,故选派甲参加数学竞赛较合适;
(2)解:5道备选题中学生甲会的3道分别记为a,b,c,不会的2道分别记为E,F,
方案一:学生甲从5道备选题中任意抽出1道的结果有:a,b,c,E,F,共5种,
抽中会的备选题的结果有a,b,c,共3种,
所以此方案学生甲可参加全国高中数学竞赛的概率.
方案二:学生甲从5道备选题中任意抽出3道的结果有:,共10种,
抽中至少2道会的备选题的结果有:,共7种,
所以此方案学生甲可参加全国高中数学竞赛的概率,
因为,所以学生甲选择方案二可参加全国高中数学竞赛的可能性更大.
【解析】【分析】(1)分别计算甲、乙两人的平均分与方差,可得平均分相同,比较方差选派成绩稳定的甲即可求解;
(2)分别计算方案一与方案二甲参赛的概率,比较大小即可求解.
25.【答案】(1)解:由对餐厅评分的频率分布直方图,
得对餐厅“满意度指数”为4的频率为,
所以,对餐厅评价“满意度指数”为4的人数为(人).
(2)解:设“对餐厅评价‘满意度指数’比对餐厅评价‘满意度指数’低”为事件.
记“对餐厅评价‘满意度指数’为3”为事件;“对餐厅评价‘满意度指数’为4”为事件;
“对餐厅评价‘满意度指数’为4”为事件;“对餐厅评价‘满意度指数’'为5”为事件.
所以,,
由频率估计概率得:,.
因为事件与事件,事件与事件,事件与事件都相互对立,
所以
,
所以该学生对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率为0.32.
(3)解:设对餐厅“满意度指数”为,对餐厅“满意度指数”为,则
随机变量的取值有,
,
所以对餐厅“满意度指数”的分布列为:
3 4 5
0.2 0.4 0.4
随机变量的取值有,
,
所以餐厅“满意度指数”的分布列为:
3 4 5
0.1 0.55 0.35
所以,,
因为,
所以如果从学生对,两家餐厅评价的“满意度指数”的期望角度看,会选择餐厅用餐.
【解析】【分析】(1)根据频率分布直方图的性质可得结果.
(2)由相互独立事件和互斥事件的概率求和即可.
(3)分布求出对餐厅和B餐厅“满意度指数”的期望,通过比较期望大小可得结论.
26.【答案】(1)解:由频率分布直方图知,学生成绩在内的频率分别为:
,显然学生成绩在内的频率最大,
所以估计该校全体学生成绩的众数为;
平均数;
显然第71百分位数,由,解得,
所以第71百分位数为.
(2)解:显然样本中高一、高二、高三年分别抽取了人、人、人,
记样本中高一学生的成绩为,高二学生的成绩为,
高三学生的成绩为,
于是,,,
因此,解得,
样本中三个年级成绩的方差,
高一、高二、高三年级学生成绩的平均数分别为,方差分别为,
则有,,
,
同理,,
因此
,解得,
所以估计高三年级学生成绩的平均数,高二年级学生成绩的方差.
【解析】【分析】(1)根据给定的频率分布直方图,利用频率分布直方图估计众数、平均数、百分位数的方法求解作答.
(2)根据表中数据,利用分层抽样结合平均数、方差的定义计算作答.
27.【答案】(1)解:由频率分布直方图得: ,
解得 .
(2)解:由频率分布直方图得 的频率为 ,
的频率为 ,
所以估计参与调查人群的样本数据的 分位数为 .
(3)解:20人中,年龄在 中的有 人,记为A,B,
年龄在 中的有 人记为a,b,c,
从年龄在 的5人中随机抽取两位,基本事件有: ,共10种,
两人恰有一人的年龄在在 内的基本事件有: ,共6种,
所以两人恰有一人的年龄在 内的概率为 .
【解析】【分析】(1)根据频率分布直方图的性质,由 求解.(2)根据频率分布直方图得到 的频率为 , 的频率为 ,再由 分位数定义求解.(3)根据频率分布直方图,先得到20人中,年龄在 和 中的人数,然后按照古典概型,先求得从年龄在 的5人中随机抽取两位的基本事件的总数,再得到两人恰有一人的年龄在在 内的基本事件数,代入公式 求解.
28.【答案】(1)解: 使用A款订餐软件的商家中“平均送达时间”不超过30分钟的商家共有 个.
(2)解: 依题意可得,使用A款订餐软件的商家中“平均送达时间”的众数为55,
由频率分布直方图可判断中位数位于
设中位数为x,则 ,解得 .
(3)解: 使用款A订餐软件的商家中“平均送达时间”的平均数为
使用B款订餐软件的商家中“平均送达时间”的平均数为
所以选 款订餐软件.
【解析】【分析】(1)根据频率分布直方图计算出概率即可求出频数.(2)利用频率分布直方图能求出使用 款订餐软件的商家中“平均送达时间”的众数,中位数.(3)使用B款订餐软件的商家中“平均送达时间”的平均数为35,小于A款订餐软件的商家中“平均送达时间”的平均数40,以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择B款订餐.
29.【答案】(1)解:由题可知, ,解得 .
(2)解:根据频率分布直方图的平均数的计算公式,
可得平均分的估计值为 分.
(3)解:由(2)可知,规定物理成绩高于96分的为优秀,
所以 .
估计该校学生物理成绩的优秀率为10%.
【解析】【分析】(1)利用已知条件结合频率分布直方图,再结合频率之和为1,进而求出a的值。
(2)利用已知条件结合频率分布直方图,进而估计出这次物理成绩的平均分。
(3) 由(2)可知,规定物理成绩高于96分的为优秀, 再利用已知条件结合频率等于频数除以样本容量,进而估计出该校学生物理成绩的优秀率。
30.【答案】(1)解:若抽取等级为5的零件的概率为0.1,则n=0.1,m=1﹣0.05﹣0.15﹣0.35﹣0.1=0.35,
综上所述,m=035,n=0.1;
(2)解:在(1)的条件下,等级为1的零件共有40×0.05=2(个),等级为5的零件共有40×01=4(个),这两个等级的零件共6个,
任意抽取2个,不同的选法共有=15(种),
如果抽取的2个零件等级恰好相同,不同的选法一共有+=7(种),所以抽取的2个零件等级恰好相同的概率是,
综上所述,抽取的2个零件等级恰好相同的概率是.
【解析】【分析】(1)根据频率分布表得0.05+m+0.15+0.35+n=1,进而求解;
(2) 先求出等级为1和5的零件个数,再利用古典概型概率公式计算求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
9.2 用样本估计总体 解答题专项
一、解答题
1.(2023高二上·柳州开学考)某市3000名市民参加亚运会相关知识比赛,成绩统计如图所示.
(1)求a的值,并估计该市参加考试的3000名市民中,成绩在[80,90)上的人数;
(2)若在本次考试中前1500名参加复赛,则进入复赛市民的分数应当如何制定(结果用分数表示).
2.(2023高一下·绍兴月考)第19届亚运会将于2023年9月23日至10月8日在杭州举行,而亚运会志愿者的服务工作是举办一届成功的亚运会的重要保障.为配合亚运会志愿者选拔,某高校举行了志愿者选拔面试,面试成绩满分100分,现随机抽取了80名候选者的面试成绩,绘制成如下频率分布直方图.
(1)求的值,并估计这80名候选者面试成绩平均值,众数,中位数;(同一组中的数据用该组区间的中点值作代表,中位数精确到0.1)
(2)乒乓球项目场地志愿服务需要3名志愿者,有3名男生和2名女生通过该项志愿服务选拔,需要通过抽签的方式决定最终的人选,现将3张写有“中签”和2张写有“未中签”字样的字条随机分配给每一位候选人,求中签者中男生比女生多的概率.
3.某市政府为了节约生活用水,计划对居民生活用水费用实施阶梯式水价制度,即确定每户月人均用水量标准M(单位:立方米),月人均用水量不超过M的部分按平价收费,超出M的部分按议价收费.现随机抽取200户进行调查,抽取的用户月人均用水量的频率分布直方图如图所示.
(1)求频率分布直方图中的值;
(2)如果希望的用户月人均用水量不超过标准M,那么标准M定为多少比较合理?
(3)若从月人均用水量在,,三组的用户中采用按比例分层抽样的方法选取6户参加节水座谈会,再从6户中随机地抽2户发言,求发言的2户来自不同组的概率.
4.(2023高一下·余姚期末)某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100)作为样本(样本容量为)进行统计,按照,,,,的分组作出频率分布直方图,已知得分在,的频数分别为8,2.
(1)求样本容量和频率分布直方图中的的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中至少有一人得分在内的概率.
5.(2023高二下·绍兴期末)中国电动汽车重大科技项目的研发开始于2001年,经过一系列的科技攻关以及奥运、世博、“十城千辆”示范平台等应用拉动,中国电动汽车建立起了具有自主知识产权的全产业链技术体系.汽车工业协会的最新数据显示,2022年中国电动汽车销量达491万辆,是2010年的400多倍.某人打算购买一款国产电动汽车,调查了100辆该款车的续航里程,得到频率分布表如下:
续航里程(单位:km) 频数 频率
3 0.03
10 0.10
30 0.30
35 0.35
15 0.15
7 0.07
(1)在图中作出频率分布直方图;
(2)根据(1)中作出的频率分布直方图估计该款车续航里程的众数与平均数.
(同一组中的数据以该组区间的中间值为代表)
6.(2023高一下·安徽月考)某果园试种了两个品种的桃树各10棵,并在桃树成熟挂果后统计了这20棵桃树的产量如下表,记两个品种各10棵产量的平均数分别为和,方差分别为和.
(单位:) 60 50 45 60 70 80 80 80 85 90
(单位:) 40 60 60 80 80 55 80 80 70 95
(1)求,,,;
(2)果园要大面积种植这两种桃树中的一种,依据以上计算结果分析选种哪个品种更合适 并说明理由.
7.(2020高一下·永寿月考)如图,从参加环保知识竞赛的学生中抽出 名,将其成绩(均为整数)整理后画出的频率分布直方图如下:观察图形,回答下列问题:
(1)求 这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率( 分及以上为及格).
8.某校举行了一次高一年级数学竞赛,笔试成绩在50分以上(包括50分,满分100分)共有100人,分成[50,60)、[60,70)、[70,80)、[80,90)、[90,100]五组,得到如图所示频率分布直方图.
(1)根据频率分布直方图估计这次数学竞赛成绩的平均数和中位数(中位数精确到0.1);
(2)为进一步了解学困生的学习情况,从数学成绩低于70分的学生中,通过分层随机抽样的方法抽取6人,再从这6人中任取3人,求此3人分数都在[60,70)的概率.
9.(2023高二上·朝阳开学考)某工厂生产某款产品,该产品市场评级规定:评分在10分及以上的为一等品,低于10分的为二等品.下面是检验员从一批产品中随机抽取的10件产品的评分:
9.6 10.1 9.7 9.8 10.0 9.7 10.0 9.8 10.1 10.2
经计算得,其中为抽取的第i件产品的评分,.
(1)求这组样本平均数和方差;
(2)若厂家改进生产线,使得生产出的每件产品评分均提高0.2.根据以上随机抽取的10件产品改进后的评分,估计改进后该厂生产的产品评分的平均数和方差;
(3)在第(2)问前提下,再从改进后生产的产品中随机抽取的10件产品,估计这10件产品平均等级是否为一等品?说明理由.
10.小晟统计了他6月份的手机通话明细清单,发现自己该月共通话100次,小晟将这100次通话的通话时间(单位:分钟)按照,,,,,分成6组,画出的频率分布直方图如图所示.
(1)求a的值;
(2)求通话时间在区间内的通话次数;
(3)试估计小晟这100次通话的平均时间(同一组中的数据用该组区间的中点值作代表).
11.某工厂有甲,乙两个车间生产同一种产品,甲车间有工人200人,乙车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,甲车间抽取的工人记作第一组,乙车间抽取的工人记作第二组,并对他们中每位工人生产完成的一件产品的事件(单位:min)进行统计,按照,,,进行分组,得到下列统计图.
(1)分别估算两个车间工人中,生产一件产品时间少于75min的人数;
(2)分别估计两个车间工人生产一件产品时间的平均值,并推测哪个车间工人的生产效率更高?
(3)从第一组生产时间少于75min的工人中随机抽取2人,求抽取2人中,恰有1人生产时间少于65min的概率.
12.某研究小组经过研究发现某种疾病的患病者与未患病者的某项医学指标有明显差异,经过大量调查,得到如下的患病者和未患病者该指标的频率分布直方图:
利用该指标制定一个检测标准,需要确定临界值,将该指标大于的人判定为阳性,小于或等于的人判定为阴性.此检测标准的漏诊率是将患病者判定为阴性的概率,记为;误诊率是将未患病者判定为阳性的概率,记为.假设数据在组内均匀分布.
(1)当漏诊率时,求临界值和误诊率;
(2)已知一次调查抽取的未患病者样本容量为100,且该项医学指标检查完全符合上面频率分布直方图(图2),临界值,从样本中该医学指标在上的未患病者中随机抽取2人,则2人中恰有一人为被误诊者的概率是多少?
13.为了解某市家庭用电量的情况,统计部门随机调查了200户居民去年一年的月均用电量(单位:),将全部数据按区间分成8组,得到如下的频率分布直方图:
(1)求图中a的值;并估计这200户居民月用电量的平均值(同一组中的数据用该组区间的中点值为代表);
(2)为了既满足居民的基本用电需求,又提高能源的利用效率,市政府计划采用阶梯电价,使75%的居民缴费在第一档,20%的居民缴费在第二档,其余5%的居民缴费在第三档,试基于统计数据确定各档月均用电量的范围(计算百分位数时,结果四舍五入取整数).
14.俄罗斯与乌克兰的军事冲突导致石油、天然气价格飙升.燃油价格问题是人们关心的热点问题,某网站为此进行了调查.现从参与者中随机选出100人作为样本,并将这100人按年龄分组:第1组,第2组,第3组,第4组,第5组,得到的频率分布直方图如图所示
(1)求样本中数据落在的频率;
(2)求样本数据的第60百分位数;
(3)若将频率视为概率,现在要从和两组中用分层抽样的方法抽取6人,再从这6人中随机抽取2人进行座谈,求抽取的2人中至少有1人的年龄在这一组的概率.
15.(2023高二上·梅河口开学考)为了解学生的周末学习时间(单位:小时),高一年级某班班主任对本班名学生某周末的学习时间进行了调查,将所得数据整理绘制出如图所示的频率分布直方图,根据直方图所提供的信息:
(1)求该班学生周末的学习时间不少于小时的人数;
(2)估计这名同学周末学习时间的分位数;
(3)如果用该班学生周末的学习时间作为样本去推断该校高一年级全体学生周末的学习时间,这样推断是否合理?说明理由.
16.(2023高一下·台州期末)第19届亚运会将于2023年9月23日至10月8日在杭州举行,为了弘扬奥林匹克和亚运精神,某学校对全体高中学生组织了一次关于亚运会相关知识的测试.从全校学生中随机抽取了100名学生的成绩作为样本进行统计,测试满分为100分,并将这100名同学的测试成绩分成5组,绘制成了如图所示的频率分布直方图.
(1)求频率分布直方图中的值,并估计这100名学生的平均成绩;
(2)用样本频率估计总体,如果将频率视为概率,从全校学生中随机抽取3名学生,求3名学生中至少有2人成绩不低于80分的概率.
17.(2023高一下·马鞍山期末)某小学对在校学生开展防震减灾教育,进行一段时间的展板学习和网络学习后,学校对全校学生进行问卷测试(满分分).现随机抽取了部分学生的答卷,得分的频数统计表和对应的频率分布直方图如图所示:
得分
人数
(1)求,的值,并估计全校学生得分的平均数;
(2)根据频率分布直方图,估计样本数据的和分位数.
18.(2023高二下·嘉定期末)某校高二年级一个班有60名学生,将期中考试的数学成绩(均为整数)分成六段:,得到如图所示的频率分布直方图,
(1)求的值;
(2)用分层随机抽样的方法从中抽取一个容量为20的样本,已知甲同学的成绩在,乙同学的成绩在,求甲乙至少一人被抽到的概率.
19.(2023高二下·杨浦期末) 某校高二年级共有学生200人,其中男生120人,女生80人.为了了解全年级学生上学花费时间(分)的信息,按照分层抽样的原则抽取了样本,样本容量为20,并根据样本数据信息绘制了茎叶图和频率分布直方图.由于保存不当,茎叶图中有一个数据不小心被污染看不清了(如图),频率分布直方图纵轴上的数据也遗失了.
(1)根据茎叶图提供的有限信息,求频率分布直方图中和的值,指出样本的“中位数、平均数、众数、方差、极差”中,哪些已经能确定,并计算它们的值;
(2)通过对样本原始数据的计算,得到男生上学花费时间的样本均值为30(分),女生的样本均值为27.75(分),试计算被污染的数值,并根据样本估计该年级全体学生上学花费时间的“中位数、平均数、方差”.
20.(2023高二下·成都期末)现在的高一年级学生将会是四川省首届参加新高考的学生,高考招生计划按历史科目组合与物理科目组合分别编制.为了了解某校高一学生的物理学习情况,在一次全年级物理测试后随机抽取了100名学生的物理成绩,将成绩分为,,,,,共6组,得到如图所示的频率分布直方图,记分数低于60分为不及格.
(1)求直方图中a的值,并估计本次物理测试的及格率;
(2)在样本中,采取分层抽样的方法从成绩不及格的学生中抽取6名作试卷分析,再从这6名学生中随机抽取2名做面对面交流,求2名面对面交流学生的成绩均来自的概率.
21.(2023高一下·衢州期末)随着现代社会物质生活水平的提高,中学生的零花钱越来越多,消费水平也越来越高,因此滋生了一些不良的攀比现象.某学校为帮助学生培养正确的消费观念,对该校学生每周零花钱的数额进行了随机调查,现将统计数据按,,…,分组后绘成如图所示的频率分布直方图,已知.
(1)求频率分布直方图中,的值;
(2)估计该校学生每周零花钱的第55百分位数;
(3)若按照各组频率的比例采用分层随机抽样的方法从每周零花钱在内的人中抽取11人,求内抽取的人数.
22.某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按照 , , , 分成9组,制成样本的频率分布直方图如图所示.
(1) 求图中 的值;
(2) 估计该校高一学生周末“阅读时间”的中位数;
(3) 在 , 这两组中采用分层抽样抽取7人,再从7人中随机抽取2人,求抽取的两人恰好都在一组的概率.
23.(2023高二下·玉林期中)全民健身旨在全面提高国民体质和健康水平,倡导全民做到每天参加一次以上的健身活动,学会两种以上健身方法,每年进行一次体质测定.为响应全民健身号召,某单位在职工体测后就某项健康指数(百分制)随机抽取了30名职工的体测数据作为样本进行调查,具体数据如茎叶图所示,其中有1名女职工的健康指数的数据模糊不清(用x表示),已知这30名职工的健康指数的平均数为76.2.
(1)根据茎叶图,求样本中男职工健康指数的众数和中位数;
(2)根据茎叶图,按男女用分层抽样从这30名职工中随机抽取5人,再从抽取的5人中随机抽取2人,求抽取的2人都是男职工的概率;
(3)经计算,样本中男职工健康指数的平均数为81,女职工现有数据(即剔除x)健康指数的平均数为69,方差为190,求样本中所有女职工的健康指数的平均数和方差(结果精确到0.1).
24.(2023高一下·安徽竞赛)某学校需要从甲、乙两名学生中选一人参加全国高中数学竞赛,现整理了近期两人5次模拟考试的成绩,结果如下表:
第一次 第二次 第三次 第四次 第五次
甲的成绩(分) 78 80 65 85 92
乙的成绩(分) 75 86 70 95 74
(1)如果根据甲、乙两人近5次的考试成绩,你认为选谁参加较合适?并说明理由;
(2)如果按照如下方案推荐参加全国高中数学竞赛:
方案一:每人从5道备选题中任意抽出1道,若答对,则可参加全国高中数学竞赛,否则被淘汰;
方案二:每人从5道备选题中任意抽出3道,若至少答对其中2道,则可参加全国高中数学竞赛,否则被淘汰.
已知学生甲只会5道备选题中的3道,那么学生甲选择哪种答题方案可参加全国高中数学竞赛的可能性更大?并说明理由.
25.(2023高二下·普宁月考)某大学为调研学生在,两家餐厅用餐的满意度,从在,两家餐厅都用过餐的学生中各随机抽取了200人,每人分别对这两家餐厅进行评分,满分为60分.整理评分数据,将分数分成6组:,,,,,,得到餐厅分数的频率分布直方图和餐厅分数的频数分布表:
餐厅分数的频数分布表:
分数区间 频数
4
6
10
30
80
70
定义学生对餐厅评价的“满意度指数”如下:
分数
满意度指数 3 4 5
(1)在抽样的200人中,求对餐厅评价“满意度指数”为4的人数;
(2)从该校在,两家餐厅都用过餐的学生中随机抽取1人进行调查,试估计其对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率;
(3)如果从,两家餐厅中选择一家用餐,从期望的角度你会选择哪一家?并说明理由.
26.(2023·黄山模拟)为了深入学习领会党的二十大精神,某高级中学全体学生参加了《二十大知识竞赛》,试卷满分为100分,所有学生成绩均在区间分内,已知该校高一 高二 高三年级的学生人数分别为800 1000 1200现用分层抽样的方法抽取了300名学生的答题成绩,绘制了如下样本频率分布直方图.
年级 样本平均数 样本方差
高一 60 75
高二 63
高三 55
(1)根据样本频率分布直方图估计该校全体学生成绩的众数 平均数 第71百分位数;
(2)已知所抽取各年级答题成绩的平均数 方差的数据如下表,且根据频率分布直方图估计出总成绩的方差为140,求高三年级学生成绩的平均数,和高二年级学生成绩的方差.
27.树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,现从参与调查的人群中随机选出20人的样本,并将这20人按年龄分组:第1组 ,第2组 ,第3组 ,第4组 ,第5组 ,得到的频率分布直方图如图所示
(1)求a的值.
(2)根据频率分布直方图,估计参与调查人群的样本数据的 分位数(保留两位小数).
(3)若从年龄在 的人中随机抽取两位,求两人恰有一人的年龄在 内的概率.
28.随着移动互联网的发展,与餐饮美食相关的手机 软件层出不穷,现从某市使用A和B两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:
(1)使用A订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个?
(2)试估计该市使用A款订餐软件的商家的“平均送达时间”的众数及中位数;
(3)如果以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择一款订餐,你会选择哪款?
29.(2020高一下·安徽月考)某校为了解高一1000名学生的物理成绩,随机抽查部分学生期中考试的成绩,将数据分成 , , , 4组,绘制成如图所示的频率分布直方图.
(1)求a的值;
(2)根据频率分布直方图,估计这次物理成绩的平均分(用组中值代替各组数据的平均值);
(3)若在本次考试中,规定物理成绩比平均分高15分以上的为优秀,估计该校学生物理成绩的优秀率(用百分数表示).
30.(2023高二上·柳州开学考)某种零件按质量标准分为1,2,3,4,5五个等级.现从一批该零件中随机抽取40个,对其等级进行统计分析,得到频率分布表如表:
等级 1 2 3 4 5
频率 0.05 m 0.15 0.35 n
(1)若抽取等级为5的零件的概率为0.1,求m,n;
(2)在(1)的条件下,从等级为1和5的所有零件中任意抽取2个,求抽取的2个零件等级恰好相同的概率.
答案解析部分
1.【答案】(1)解:由已知得:(2a+2a+3a+6a+7a)×10=1得:a=0.005,
故成绩在[80,90)上的频率为0.03×10=0.3,
故成绩在[80,90)上的人数为:3000×0.3=900(人);
(2)解:设50%分位数为x,则(2×0.005+3×0.005)×10+7×0.05××10=0.5,
解得x=(分),故进入复赛市民的分数应当不低于分.
【解析】【分析】(1)根据所以小长方形的面积和为1求解a,再求得成绩在[80,90)的频率,根据频数计算公式 人数;
(2)结合已知数据根据频率分布直方图求50%分位数即可.
2.【答案】(1)解:由频率分布直方图可知,解得,
,
众数为70,
因为前2组的频率和为,前3组的频率和为,
所以中位数在第3组,设中位数为,则
,解得,
所以中位数为.
(2)解:记3名男生分别为,记2名女生分别为,则所有抽签的情况有:
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签,共有10种情况,
其中中签者中男生比女生多的有:未中签,中签;未中签,中签;
未中签,中签;未中签,中签;未中签,中签;
未中签,中签;未中签,中签,共7种,
所以中签者中男生比女生多的概率为.
【解析】【分析】(1)首先根据频率和为1可列出关于a的方程并解出a的值,其次根据平均数、众数的定义即可求出平均数、众数,求中位数需要先判断中位数的位置,再列方程求解;
(2)首先利用列举法列出所有抽签的情况,可知其中中签者中男生比女生多的共有7种,即可计算概率.
3.【答案】(1)解:因为图中所有矩形面积之和为1,
所以,
解得.
(2)解:由图象可知,月人均用水量低于2立方米的居民占比为
,
月人均用水量低于立方米的居民占比为
,
根据分位数的含义可知,,
且,解得.
(3)解:由图象可知,内的频率为,内的频率为,内的频率为,
所以,根据分层抽样知,应从中抽3户,记作,中抽2户,记作,中抽1户,记作.
则从这6户中抽取2户有,,,,,,,,,,,,,,,共包含个等可能的样本点,
满足发言的2户来自不同组的有,,,,,,,,,,共包含个样本点,
根据古典概型可知,发言的2户来自不同组的概率.
【解析】【分析】 ( 1 )根据频率分布直方图中小矩形面积之和为1,列出方程,求解即可得 的值;
( 2 )利用百分位数的概念列出方程,求解即可得出M的值;
( 3 )求出3个区间内的频率,根据分层抽样得出每个区间应该抽取的人数,然后列举出所有的点,再根据古典概型概率公式,即可求出发言的2户来自不同组的概率.
4.【答案】(1)解:由题意可知,样本容量n==50,
,x=0.100﹣0.004﹣0.010﹣0.016﹣0.040=0.030;
(2)解:设本次竞赛学生成绩的中位数为m,平均分为,
则[0.016+0.03]×10+(m﹣70)×0.040 =0.5,解得,
=(55×0.016+65×0.030+75×0.040+85×0.010+95×0.004]×10=70.6,
(3)解:由题意可知,分数在[80,90)内的学生有5人,记这5人分别为a1,a2,a3,a4,a5,
分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种,
分别为:(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a1,b1),(a1,b2),(a2,a3),
(a2,a4),(a2,a5),(a2,b1),(a2,b2),(a3,a4),(a3,a5),(a3,b1),
(a3,b2),(a4,a5),(a4,b1),(a4,b2),(a5,b1),(a5,b2),(b1,b2).
其中2名同学的分数都不在[90,100]内的情况有10种,分别为:
(a1,a2),(a1,a3),(a1,a4),(a1,a5),(a2,a3),(a2,a4),(a2,a5),(a3,a4),(a3,a5),(a4,a5).
∴所抽取的2名学生中至少有一人得分在[90,100]内的概率.
【解析】【分析】本题主要考查频率分布直方图、频率与频数的关系及古典概型的计算公式等有关知识的综合运用,
(1)根据得分在,的频数分别为8和2,再结合频率分布直方图即可求出x、y的值;
(2)根据频率分布直方图中提供的数据信息求解中位数和平均分即可;
(3)运用列举法先将分数在[90,100]内的学生有2人,记这2人分别为b1,b2.抽取的2名学生的所有情况有21种分别列出,再将其中2名同学的分数都不在[90,100]内的情况有10种分别列出,最后利用古典概型计算公式求解即可.
5.【答案】(1)解:
(2)解:众数:275
平均数:
【解析】【分析】(1)根据频率分布表作出频率分布直方图;
(2)根据频率分布直方图最高矩形底边中点值为该款车续航里程的众数,将每个矩形底边中点值乘以对应矩形面积全部结果相加得到平均数。
6.【答案】(1)解:,
,
,
.
(2)解:由可得两个品种平均产量相等,
又,则品种产量较稳定,故选择品种.
【解析】【分析】(1)利用平均数和方差定义代入数据计算;
(2)比较 两个品种的平均产量和产量的稳定程度。
7.【答案】(1)解: 这一组的频率为 ,
这一组的频数为 ;
(2)解:估计这次环保知识竞赛的及格率( 分及以上为及格) .
【解析】【分析】(1) 根据题意由已知的频率分布图的数据即可计算出结果。
(2)由概率的定义结合题意即可得出答案。
8.【答案】(1)由,解得,
这次数学竞赛成绩的平均数为,
前2组的频率和为,前3组的频率和为,
所以中位数为.
(2)分层抽样抽取的6人中,数学成绩位于的有人,记为a,b.
数学成绩位于的有人,记为A、B、C、D,
从6人中任取3人,基本事件有:abA、abB、abC、abD、aAB、aAC、aAD、aBC、aBD、aCD,bAB、bAC,bAD,bBC、bBD,bCD,ABC,ABD、ACD、BCD,共20种,
其中3人分数都在的有ABC、ABD、ACD、BCD,共4种,
所以从6人中任取3人,分数都在的概率为.
【解析】
【分析】(1)由频率分布直方图列方程,可得, 这次数学竞赛成绩的平均数为,根据中位数的定义可求得样本的中位数;
(2)分层抽样抽取的6人中,数学成绩位于的有人,记为a,b. 数学成绩位于的有4人,记为 A、B、C、D ,列举出所有的基本事件,利用古典概型的概率公式即可求解.
9.【答案】(1)解:样本平均值
样本方差.
(2)解:估计改进后该厂生产的产品评分的平均数,
方差.
(3)解:可以认为是一等品.因为改进后该厂生产的产品评分由样本数据估计平均数为,所以可以认为这10件产品平均等级为一等品不一定是一等品.
因为样本数据具有随机性,所以新样本平均值不一定达到10分及以上,所以新样本平均等级不一定是一等品.
【解析】【分析】(1)利用平均数和方差的定义求解;
(2)根据平均数的性质和方差的性质求解;
(3)从平均数角度分析或从抽样具有随机性角度分析.
10.【答案】(1)解:由,
得.
(2)解:因为通话时间在区间内的频率为,
所以通话时间在区间内的通话次数为.
(3)解:这100次通话的平均时间的估计值为分钟.
【解析】【分析】(1)根据频率之和为1列方程求得;
(2) 通话时间在区间内的频率为, 所以通话时间在区间内的通话次数为;
(3)根据频率分布直方图求得平均数,即可得解.
11.【答案】(1)解:第一组工人20人,其中在75min内(不含75min)生产完成一件产品的有6人,
∴甲车间工人中生产一件产品时间少于75min的人数为(人),
第二组工人40人.其中在75min内(不含75min)生产完成一件产品的有
人,
∴乙车间工人中生产一件产品时间少于75min的人数为(人).
(2)解:第一组平均时间为:,
第二组平均时间为:,
∵,∴乙车间工人生产效率更高.
(3)解:由题意得,第一组生产时间少于75min的工人有6人,
其中生产时间少于65min的有2人,分别用,代表,
生产时间不少于65min的工人用,,,代表,
抽取2人基本事件空间为:
,共15个基本事件.
设事件A:恰有1人生产时间少于65min,
则.
【解析】【分析】 (1) 根据题意结合频率分布直方图分析运算;
(2) 根据题意结合平均数公式运算求解,并对比分析;
(3)根据分层抽样求各层人数,利用列举法结合古典概型分析求解.
12.【答案】(1)解:依题可知,图1第一个小矩形的面积为,所以,
所以,解得,
(2)解:由题可知,100个未患病者中,该项医学指标在中的有人,
其中被误诊者有人,
记随机抽取的2人恰有一人为被误诊者为事件A.分别用a,b,c,d,E,F表示这6人,E,F代表被误诊的2人,
样本空间,
事件,故,,
,故2人中恰有一人为被误诊者的概率是.
【解析】【分析】(1)根据漏诊率的定义利用概率为0.5%可求得,再根据误诊率的定义可求得;
(2)先求出指标在中的人数,再求出其中被误诊的人数,利用列举法,将样本空间的结果一 一列举,并找到随机抽取的2人恰有一人为被误诊者所包含的样本点的个数,结合古典概型的概率计算公式可得结果.
13.【答案】(1)解:由直方图可得,样本落在
的频率分别为
,由,解得,
则样本落在的频率分别为,所以月用电量的平均值为
(2)解:为了使的居民缴费在第一档,需要确定月用电量的分位数;
的居民缴费在第二档,还需要确定月用电量的分位数.
因为,
则使的居民缴费在第一档,月用电量的分位数位于区间内,
于是.
又,所以对应的用电量为350.
所以第一档的范围是,第二档的范围是,第三档的范围是.
【解析】【分析】 (1)根据所有小长方形的面积和为1列方程求a的值,再根据频率分布直方图计算平均值;
(2)为了使75%的居民缴费在第一档,需要确定月用电量的分位数;使20%的居民缴费在第二档
需要确定月用电量的分位数,结合百分数的计算方法求解.
14.【答案】(1)解:由频率分布直方图可知,样本中数据落在的频率为
(2)解:样本数据的第60百分位数落在第四组,且第60百分位数为
(3)解:与两组的频率之比为,现从和两组中用分层抽样的方法抽取6人,则组抽取2人,记为,,组抽取4人,记为1,2,3,4.
所有可能的情况为,,,,,,,,,,,,,,,共15种.
其中至少有1人的年龄在的情况有,,,,,,,,,共9种,故所求概率
【解析】【分析】(1)根据频率分布直方图分析运算;
(2)根据题意结合百分位数的定义分析求解;
(3) 先根据分层抽样求各层人数,再利用列举法和古典概型运算求解.
15.【答案】(1)解:由图可知,该班学生周末的学习时间不少于20小时的频率为
则名学生中周末的学习时间不少于20小时的人数为.
(2)解:学习时间在小时以下的频率为,
学习时间在小时以下的频率为,
所以分位数在,
,
则这名同学周末学习时间的分位数为.
(3)解:不合理,样本的选取只选在高一某班,不具有代表性.
【解析】【分析】(1)先根据频率分布直方图求 不少于20小时的频率 ,进而求人数;
(2)根据题意分析可得 分位数在, 结合百分位数的定义运算求解;
(3)根据随机抽样的性质分析判断.
16.【答案】(1)解:由频率分布直方图可得每组的频率依次为,
则,解得,
设平均成绩的估计值为,
则(分),
所以这100名学生的平均成绩估计值为74分.
(2)解:每个学生成绩不低于80分的概率为0.4.
3名学生中恰有2人成绩不低于80分的概率;
3名学生中恰有3人成绩不低于80分的概率;
3名学生中至少有2人成绩不低于80分的概率.
【解析】【分析】 (1) 根据频率分布直方图可得相应的频率,结合频率和为求1求t,并结合平均数公式运算求解;
(2) 根据题意用频率估计概率,进而结合独立事件概率乘法公式运算求解.
17.【答案】(1)解:由频率分布直方图可知,
得分在的频率为,
故抽取的学生答卷数为,
由,得.
所以,
得分的平均数估计值为:
.
(2)解:由图可知,内的比例为,
内的比例为,内的比例为,
内的比例为.
因此,分位数一定位于.
由,
可以估计样本数据的分位数为.
类似的,由,
可以估计样本数据的分位数为.
【解析】【分析】(1)依据频率直方图以及频率求出a、b的值,再求出全校的平均数即可.
(2)根据频率分布直方图的概念,百分位数的概念求出即可.
18.【答案】(1)解:由题意可得,
解得;
(2)解:因为总体共60名学生,样本容量为20,因此抽样比为.
其中分数段有人,分数段有人,
所以在分数段中抽取人,分数段抽取人,
设甲被抽到的事件为,乙被抽到的事件为,
则,,
则甲乙至少一人被抽到的概率为.
【解析】【分析】 (1) 根据频率和为1运算求解;
(2) 先根据分层抽样求各层人数,进而可得甲、乙被抽到的概率,结合独立事件概率乘法公式运算求解.
19.【答案】(1)解:根据直方图可以看出,组距为,的频数为1,频率为,,
的频数为,频率为,
涂抹的数不确定大小,因此不能确定中位数
众数和极差可以确定,
无论被涂抹的数字是多少,不影响众数为,
极差为
(2)解:
被污染的数值为,
样本平均数,
于是样本方差
由于涂抹的数字是,故可以确定第个数是,则中位数为
于是可估计该年级全体学生上学花费时间的中位数为,平均数为,方差为.
【解析】【分析】(1)结合茎叶图和直方图组距求出 和的值, 利用”中位数、平均数、众数、方差、极差“的定义判断其值是否可以确定,并求解 ;
(2)先根据男女平均数算出被污染的数据,利用两组数的平均值求合成后的平均值,然后由方差公式计算方差。
20.【答案】(1)解:因为,
所以,
由频率分布直方图可知,成绩不少于60分的频率为,
即及格率为.
(2)解:由分层抽样可知,成绩在,分别抽取的人数为,
不妨设成绩在的2人为,成绩在的4人为,
则任取2人的所有基本事件为,,共15个,其中2人成绩都在的有6个,
所以由古典概型知.
【解析】【分析】(1)根据频率分布直方图直接计算即可得解.
(2)由分层抽样得出成绩在两个区间的人数,列出基本事件,由古典概型求解即可.
21.【答案】(1)解:,即
又,所以,.
(2)解:前3组的频率和为,
前4组的频率和为,
∴第55百分位数位于第4组内.
∴估计第55百分位数为元.
(3)解:,,这三组的频率分别为,,,比例为,
则从内抽取的人数分别为.
【解析】【分析】(1)由频率和为1可得,结合已知条件,解方程组即可求出.
(2)利用百分位数的定义,先判断第55百分位数所在的区间,结合频率直方图即可求出.
(3)先算出各组的频数,再根据各组的比例即可求出.
22.【答案】(1)解:由题意,高一学生周末“阅读时间”在 , , , 的概率分别为 0.04,0.08,0.20,0.25,0.07,0.04,0.02,
由 ,所以
(2)解:设该校高一学生周末“阅读时间”的中位数为 小时,
因为前5组频率和为 ,前4组频率和为 ,
所以 ,
由 ,得
(3)解:在 , 这两组中的人分别有15人、20人,采用分层抽样抽取7人,分别为3人、 4人,再从7人中随机抽取2人,有 种,抽取的两人恰好都在一组,有 种,故所求概率为
【解析】【分析】(1)根据频率分布直方图中小长方形的面积之和等于1,求 的值;
(2)根据频率分布直方图设中位数为 ,然后列出方程求解;
(3)根据分层抽样原理结合古典概型的计算公式求解.
23.【答案】(1)解:根据茎叶图,得到样本中男职工健康指数的众数是,
中位数是;
(2)解:根据茎叶图,按男女用分层抽样从这名职工中随机抽取人,
抽样比
男职工抽(人),记为,女职工人,记为,
从这人中随机抽取人,所有的基本事件是、、、、、
、、、、共种,
抽取的人都是男职工的事件为、、,
故所求的概率为P;
(3)解:由题意知: ,解得;
所以样本中所有女职工的健康指数平均数为,
方差为.
【解析】【分析】(1)根据茎叶图中的数据,计算样本中男职工健康指数的众数和中位数;
(2)根据分层抽样的基本原理可以求出男,女职工人数,用列举法求出基本事件数,计算所求的概率值;
(3)根据题意求出x的值,再计算健康指数的平均数和方差.
24.【答案】(1)解:选派甲参加数学竞赛较合适.
由题意得,
,
,
,
由,可知甲、乙的平均分相同,但甲的成绩比乙稳定,故选派甲参加数学竞赛较合适;
(2)解:5道备选题中学生甲会的3道分别记为a,b,c,不会的2道分别记为E,F,
方案一:学生甲从5道备选题中任意抽出1道的结果有:a,b,c,E,F,共5种,
抽中会的备选题的结果有a,b,c,共3种,
所以此方案学生甲可参加全国高中数学竞赛的概率.
方案二:学生甲从5道备选题中任意抽出3道的结果有:,共10种,
抽中至少2道会的备选题的结果有:,共7种,
所以此方案学生甲可参加全国高中数学竞赛的概率,
因为,所以学生甲选择方案二可参加全国高中数学竞赛的可能性更大.
【解析】【分析】(1)分别计算甲、乙两人的平均分与方差,可得平均分相同,比较方差选派成绩稳定的甲即可求解;
(2)分别计算方案一与方案二甲参赛的概率,比较大小即可求解.
25.【答案】(1)解:由对餐厅评分的频率分布直方图,
得对餐厅“满意度指数”为4的频率为,
所以,对餐厅评价“满意度指数”为4的人数为(人).
(2)解:设“对餐厅评价‘满意度指数’比对餐厅评价‘满意度指数’低”为事件.
记“对餐厅评价‘满意度指数’为3”为事件;“对餐厅评价‘满意度指数’为4”为事件;
“对餐厅评价‘满意度指数’为4”为事件;“对餐厅评价‘满意度指数’'为5”为事件.
所以,,
由频率估计概率得:,.
因为事件与事件,事件与事件,事件与事件都相互对立,
所以
,
所以该学生对餐厅评价的“满意度指数”比对餐厅评价的“满意度指数”低的概率为0.32.
(3)解:设对餐厅“满意度指数”为,对餐厅“满意度指数”为,则
随机变量的取值有,
,
所以对餐厅“满意度指数”的分布列为:
3 4 5
0.2 0.4 0.4
随机变量的取值有,
,
所以餐厅“满意度指数”的分布列为:
3 4 5
0.1 0.55 0.35
所以,,
因为,
所以如果从学生对,两家餐厅评价的“满意度指数”的期望角度看,会选择餐厅用餐.
【解析】【分析】(1)根据频率分布直方图的性质可得结果.
(2)由相互独立事件和互斥事件的概率求和即可.
(3)分布求出对餐厅和B餐厅“满意度指数”的期望,通过比较期望大小可得结论.
26.【答案】(1)解:由频率分布直方图知,学生成绩在内的频率分别为:
,显然学生成绩在内的频率最大,
所以估计该校全体学生成绩的众数为;
平均数;
显然第71百分位数,由,解得,
所以第71百分位数为.
(2)解:显然样本中高一、高二、高三年分别抽取了人、人、人,
记样本中高一学生的成绩为,高二学生的成绩为,
高三学生的成绩为,
于是,,,
因此,解得,
样本中三个年级成绩的方差,
高一、高二、高三年级学生成绩的平均数分别为,方差分别为,
则有,,
,
同理,,
因此
,解得,
所以估计高三年级学生成绩的平均数,高二年级学生成绩的方差.
【解析】【分析】(1)根据给定的频率分布直方图,利用频率分布直方图估计众数、平均数、百分位数的方法求解作答.
(2)根据表中数据,利用分层抽样结合平均数、方差的定义计算作答.
27.【答案】(1)解:由频率分布直方图得: ,
解得 .
(2)解:由频率分布直方图得 的频率为 ,
的频率为 ,
所以估计参与调查人群的样本数据的 分位数为 .
(3)解:20人中,年龄在 中的有 人,记为A,B,
年龄在 中的有 人记为a,b,c,
从年龄在 的5人中随机抽取两位,基本事件有: ,共10种,
两人恰有一人的年龄在在 内的基本事件有: ,共6种,
所以两人恰有一人的年龄在 内的概率为 .
【解析】【分析】(1)根据频率分布直方图的性质,由 求解.(2)根据频率分布直方图得到 的频率为 , 的频率为 ,再由 分位数定义求解.(3)根据频率分布直方图,先得到20人中,年龄在 和 中的人数,然后按照古典概型,先求得从年龄在 的5人中随机抽取两位的基本事件的总数,再得到两人恰有一人的年龄在在 内的基本事件数,代入公式 求解.
28.【答案】(1)解: 使用A款订餐软件的商家中“平均送达时间”不超过30分钟的商家共有 个.
(2)解: 依题意可得,使用A款订餐软件的商家中“平均送达时间”的众数为55,
由频率分布直方图可判断中位数位于
设中位数为x,则 ,解得 .
(3)解: 使用款A订餐软件的商家中“平均送达时间”的平均数为
使用B款订餐软件的商家中“平均送达时间”的平均数为
所以选 款订餐软件.
【解析】【分析】(1)根据频率分布直方图计算出概率即可求出频数.(2)利用频率分布直方图能求出使用 款订餐软件的商家中“平均送达时间”的众数,中位数.(3)使用B款订餐软件的商家中“平均送达时间”的平均数为35,小于A款订餐软件的商家中“平均送达时间”的平均数40,以“平均送达时间”的平均数作为决策依据,从A和B两款订餐软件中选择B款订餐.
29.【答案】(1)解:由题可知, ,解得 .
(2)解:根据频率分布直方图的平均数的计算公式,
可得平均分的估计值为 分.
(3)解:由(2)可知,规定物理成绩高于96分的为优秀,
所以 .
估计该校学生物理成绩的优秀率为10%.
【解析】【分析】(1)利用已知条件结合频率分布直方图,再结合频率之和为1,进而求出a的值。
(2)利用已知条件结合频率分布直方图,进而估计出这次物理成绩的平均分。
(3) 由(2)可知,规定物理成绩高于96分的为优秀, 再利用已知条件结合频率等于频数除以样本容量,进而估计出该校学生物理成绩的优秀率。
30.【答案】(1)解:若抽取等级为5的零件的概率为0.1,则n=0.1,m=1﹣0.05﹣0.15﹣0.35﹣0.1=0.35,
综上所述,m=035,n=0.1;
(2)解:在(1)的条件下,等级为1的零件共有40×0.05=2(个),等级为5的零件共有40×01=4(个),这两个等级的零件共6个,
任意抽取2个,不同的选法共有=15(种),
如果抽取的2个零件等级恰好相同,不同的选法一共有+=7(种),所以抽取的2个零件等级恰好相同的概率是,
综上所述,抽取的2个零件等级恰好相同的概率是.
【解析】【分析】(1)根据频率分布表得0.05+m+0.15+0.35+n=1,进而求解;
(2) 先求出等级为1和5的零件个数,再利用古典概型概率公式计算求解.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
