专题5.6垂线 巩固篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练
文档属性
| 名称 | 专题5.6垂线 巩固篇 专项练习(含解析)2023-2024学年七年级数学下册人教版专项讲练 |

|
|
| 格式 | docx | ||
| 文件大小 | 673.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 11:19:04 | ||
图片预览




文档简介
专题5.6 垂线(巩固篇)(专项练习)
一、单选题
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( ).
A.有两个角相等 B.有两对角相等 C.有三个角相等 D.有四对邻补角
2.平面内,经过直线外一点画的垂线,能画出
A.1条 B.2条 C.3条 D.4条
3.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,正确的是( )
A. B. C.D.
4.如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
A.点A到直线l2的距离等于4
B.点C到直线l1的距离等于4
C.点C到AB的距离等于4
D.点B到AC的距离等于3
5.如图,在△ABC中,∠C=90,D是边BC上一点,且∠ADC=60,那么下列说法中错误的是( )
A.直线AD与直线BC的夹角为60 B.直线AC与直线BC的夹角为90
C.线段CD的长是点D到直线AC的距离 D.线段AB的长是点B到直线AD的距离
6.如图,已知直线,,则直线与重合,理由是( )
A.垂线段最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
D.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条
7.如图,,则的长度可能是( )
A.3 B.5 C.3或5 D.4.5
8.如图所示,点A到BC所在的直线的距离是指图中线段( )的长度.
A.AC B.AF C.BD D.CE
9.直线,相交于点.分别平分.下列说法正确的是( )
A.在同一直线上 B.在同一直线上
C. D.
10.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,下列结论不正确的是( )
A.∠EOB=90° B.∠DOB是∠AOE 的补角
C.∠AOC=52° D.∠AOC与∠EOD 互为余角
二、填空题
11.如果∠,∠两边分别垂直,其中∠比∠的2倍少30°,那么∠= .
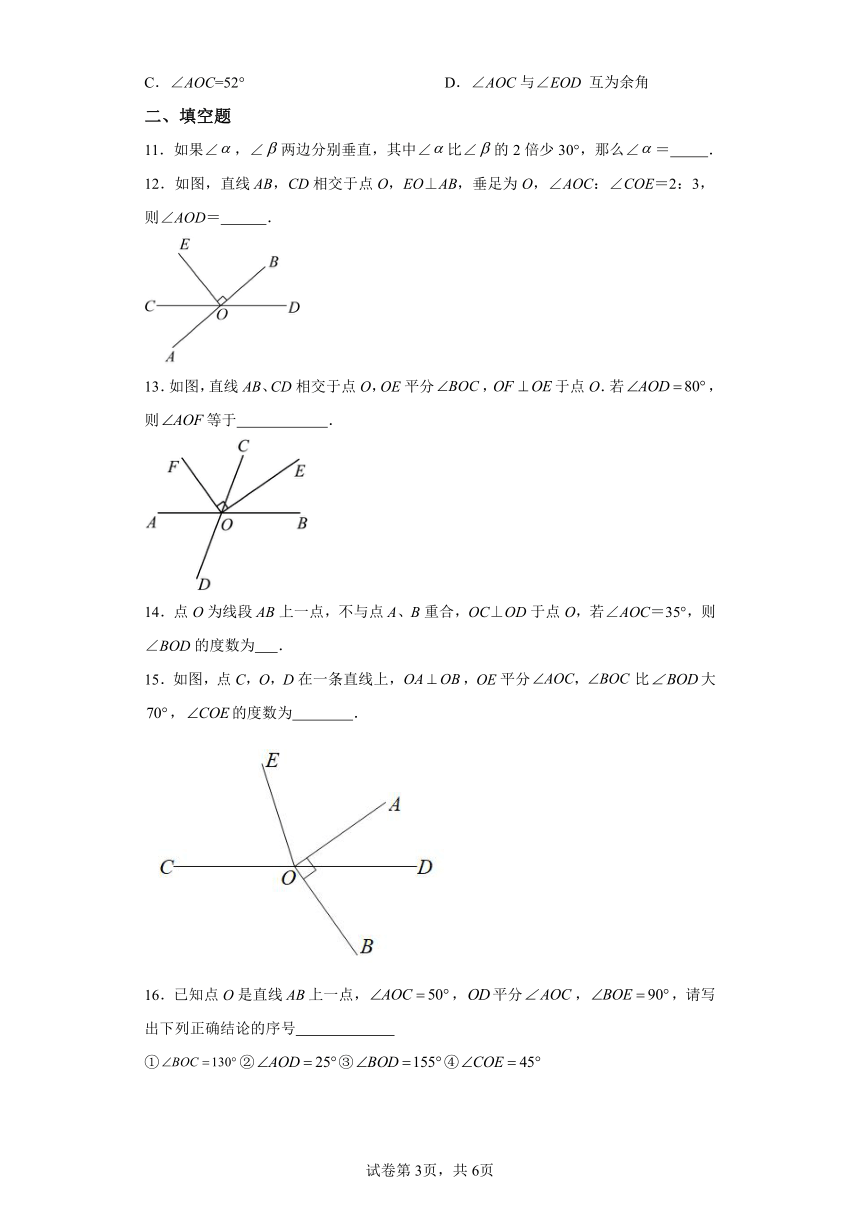
12.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=2:3,则∠AOD= .
13.如图,直线AB、CD相交于点O,OE平分,于点O.若,则等于 .
14.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
15.如图,点C,O,D在一条直线上,,OE平分比大,的度数为 .
16.已知点O是直线上一点,,平分,,请写出下列正确结论的序号
①②③④
17.如图,直线,相交于点,,垂足为点.当直线绕着点在内部转动,是的角平分线,若,则,则关于的函数关系式为 .
18.100条直线两两相交于一点,则共有对顶角(不含平角) 对,邻补角 对.
三、解答题
19.如图,A、B、C是平面内三点.
(1)按要求作图:
①作射线BC,过点B作直线l,使A、C两点在直线l两旁;
②点P为直线l上任意一点,点Q为直线BC上任意一点,连接线段AP、PQ;
(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A、B之间的距离为8,点A、C之间的距离为6,则AP+PQ的最小值为__________,依据是__________
20.如图,直线、相交于点,平分,,,求的度数.
21.如图,已知是内三条射线,平分平分.
(1)若,求的度数.
(2)若,求的度数.
(3)若,求的度数.
22.如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
23.如图,用三张卡片拼成如下图①,图②所示的两个四边形,其周长分别为、.
(1)请你根据所学知识解释:在直角三角形卡片中,“”的理由是_________.(填写正确选项的字母)
A.两点之间线段最短;B.过一点有且只有一条直线与已知直线垂直;C.垂线段最短;D.两点确定一条直线.
(2)分别计算、(用含m、n的代数式表示);
(3)比较与的大小,并说明理由.
24.点O为直线l上一点,射线均与直线l重合,如图1所示,过点O作射线和射线,使得,,作的平分线.
(1)求与的度数;
(2)作射线,使得,请在图2中画出图形,并求出的度数;
(3)如图3,将射线从图1位置开始,绕点O以每秒的速度逆时针旋转一周,作的平分线,当时,求旋转的时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】两直线相交所成的四个角中,有一个角为90°,则这两条直线互相垂直,根据的定义判断即可.
【详解】解:A、两条直线相交成四个角,如果有两个角相等,是两个对顶角相等,那么这两条直线不一定垂直,故本选项错误;
B、两条直线相交成四个角,如果有两对角相等,是两对对顶角相等,那么这两条直线不一定垂直,故本选项错误;
C、两条直线相交成四个角,则这四个角中有2对对顶角.如果三个角相等,则这四个角相等,都是直角,所以这两条直线垂直.故正确;
D、两条直线相交成四个角,如果有四对邻补角,是四对普通的邻补角,那么这两条直线不一定垂直,故本选项错误;
故选:C.
【点睛】本题主要考查了垂线的定义,对顶角的定义,邻补角的定义,是基础题,熟记概念是解题的关键.
2.A
【分析】平面内经过一点有且只有一条直线垂直于已知直线,据此可得.
【详解】经过直线l外一点画l的垂线,能画出1条垂线,
故选A.
【点睛】本题主要考查垂线,解题的关键是掌握在平面内,过一点有且只有一条直线与已知直线垂直.
3.A
【分析】满足两个条件:①经过点B.②垂直AC;由此即可判断.
【详解】解:根据垂线段的定义可知,图①线段BE,是点B作线段AC所在直线的垂线段,
故选A.
【点睛】本题考查作图-复制作图,垂线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.A
【分析】根据点到直线的距离的定义:直线外一点到这条直线的垂线段的长度,即可得到答案.
【详解】解:点A到直线l2的距离为AB的长,等于4,故A正确;
点C到直线l1的距离为AC的长,大于4,故B错误;
点C到AB的距离为BC的长,等于3,故C错误;
同理,点B到AC的距离也不是3,故D错误,
故选:A
【点睛】本题考查点到直线的距离,掌握定义是解题的关键.
5.D
【分析】根据已知角即可判断A、B;根据点到直线的距离的定义即可判断C、D.
【详解】解:A、∵∠CDA=60,
∴直线AD与直线BC的夹角是60,正确,故不符合题意;
B、∵∠ACD=90,
∴直线AC与直线BC的夹角是90,正确,故不符合题意;
C、∵∠ACD=90,
∴DC⊥AC,
∴线段CD的长是点D到直线AC的距离,正确,故不符合题意;
D、∵BD和AD不垂直,
∴线段AB的长不是点B到直线AD的距离,错误,故本选项符合题意;
故选:D.
【点睛】本题考查了点到直线的距离,以及直线与直线的夹角,注意:点到直线的距离是指该点到直线的垂线段的长.
6.B
【分析】直接利用垂线的性质进而分析得到答案.
【详解】∵,,垂足为B,
∴AB和BC重合,理由是:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
故选:B.
【点睛】本题考查了同一平面内直线的垂直关系及垂线段的知识点,解题的关键是熟悉对垂线段定义的理解.
7.D
【分析】根据垂线段最短可得3<BD<5.
【详解】解:∵AD⊥BD,BC⊥CD,AB=5,BC=3,
∴BC<BD<AB,
即3<BD<5.
故选:D.
【点睛】此题主要考查了垂线段的性质,关键是掌握垂线段最短.
8.B
【分析】根据点到直线的距离是垂线段的长度,可得答案.
【详解】点A到线段BC所在直线的距离是线段AF的长度,
故选B.
【点睛】本题考查了点到直线的距离,利用点到直线的距离的定义是解题关键.
9.D
【分析】根据角平分线的性质得到,又因为与是补角,所以,所以,所以A错误,D正确;因为,且与是对顶角,所以,所以,与共线,所以,,所以B,C均错误.
【详解】解:如图,
∵,
∵分别是的平分线,
∴,
∵是的平分线,
∴,
∴,
∴,
∴射线互相垂直,故D正确;故A错误;射线互相垂直;故C错误;故B错误.
故选:D.
【点睛】本题考查了垂线,对顶角,角平分线的定义,正确的识别图形是解题的关键.
10.B
【分析】根据垂直的定义可知,故A正确;根据互补定义,由图知和互补,故B错误;根据OE⊥AB,∠EOD=38°,结合对顶角定义,可得,故C正确;根据互余定义和对顶角定义可知,即可得到∠AOC与∠EOD 互为余角,故D正确,从而得到结论.
【详解】解:A、由于OE⊥AB,则,故该选项不符合题意;
B、由于三点共线,则,即∠DOB是∠AOE 的补角错误,故该选项符合题意;
C、由于OE⊥AB,则,再结合∠EOD=38°,根据对顶角相等可知,故该选项不符合题意;
D、由于OE⊥AB,则,从而,根据对顶角相等可得,∠AOC与∠EOD 互为余角,故该选项不符合题意;
故选:B.
【点睛】本题考查垂线的定义、互余的定义、互补的定义和对顶角相等的性质等知识点,熟记概念,准确识图并找到各个相关角度之间的数量关系是解决问题的关键.
11.或
【分析】分两种情况,当时,当,然后进行计算即可解答,
【详解】解:设为,则,
分两种情况:
当时,如图:
,
解得:,
,
当,如图:
,
解得:,
综上所述:或.
故答案为:或.
【点睛】本题考查了垂线,角的计算,根据题意画出图形,分两种情况讨论是解题的关键.
12.144°
【分析】直接利用垂直的定义得出∠AOE=90°,进而利用∠AOC:∠COE=2:3,得出∠AOC的度数,进而得出答案.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
∵∠AOC:∠COE=2:3,
∴设∠AOC=2x,∠COE=3x,
则3x+2x=90°,
解得:x=18°,
故∠AOC=36°,
则∠AOD=180°-36°=144°.
故答案为:144°.
【点睛】此题主要考查了垂直的定义以及邻补角,正确得出∠AOC度数是解题关键.
13.##50度
【分析】根据对顶角相等可得,再根据角平分线的性质得,最后根据平角的性质求解即可.
【详解】解:∵,
∴.
∵OE 平分∠BOC,
∴.
∵OF⊥OE,
∴,
∴.
故答案为:.
【点睛】本题考查了角的度数问题、垂直定义以及角平分线的定义,掌握对顶角相等、平角的定义是解题的关键.
14.55°或125°
【分析】分OC,OD在AB的同侧和异侧两种情况求解.
【详解】当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
【点睛】本题考查了垂直的定义即两直线相交,交成的四个角中有一个是直角,理解定义,学会分类是解题的关键.
15.##72.5度
【分析】根据比大,和互补,即可求出,进而由垂直性质可求出,再由角平分线性质即可得出答案.
【详解】解:∵比大,
∴设,则,
∵ ,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵OE平分,
∴.
故答案为:.
【点睛】本题考查了垂直的性质,角平分线的性质以及角的运算,掌握以上知识是解题的关键.
16.①②③
【分析】根据图形的特点及角平分线的概念依次求出各角度即可解答.
【详解】解:∵,
∴∠BOC=180°-=130°,则①正确
∵OD平分,
∴∠AOD=,则②正确
∴∠BOD=180°-∠AOD=155°,则③正确
∵
∴∠COE=-=40°,则④错误.
故答案为:①②③.
【点睛】本题主要考查角平分线、垂直、邻补角的定义以及角的和差等知识点,熟知邻补角的定义及角平分线的定义成为解答本题的关键.
17.
【分析】先由角平分线定义得:,由垂直定义和角的和差,再根据,得到与的关系,进而得解.
【详解】∵是的角平分线,,
∴.
∵,
∴,
∵,
∴.
∵,
∴,
∴,
故答案是.
【点睛】本题主要考查垂直的定义,角平分线的定义,补角的定义,由,,推导出关于的函数关系式是解本题的关键.
18. 9900 19800
【分析】由特殊情况总结出一般规律,应用规律即可求解.
【详解】解:图①中共有2对对顶角,4对邻补角,
图②中共有6对对顶角,12对邻补角,
图③中共有12对对顶角,24对邻补角,
,
根据上面的规律,直线条数与对顶角对数之间的关系为:若有n条直线相交于一点,则可形成对对顶角.对邻补角,
若100条直线相交于一点,则可形成9900对对顶角,19800对邻补角,
故答案为:9900,19800.
【点睛】本题考查有规律性的数学问题,关键是由特殊情况总结出一般规律.
19.(1)①见解析;②见解析
(2)5,垂线段最短
【分析】(1)根据题意作出图形即可;
(2)根据线段的性质即可得到结论.
【详解】(1)解:①如图1所示,射线BC,直线l即为所求;
②如图1所示,线段AP,PQ即为所求;
;
(2)解:过A作AQ⊥BC交直线l于P,
则此时,AP+PQ的值最小,
∵点A到直线BC的距离为5,
∴AP+PQ的最小值为5,
依据是垂线段最短,
故答案为:5,垂线段最短.
【点睛】本题考查了点到直线的距离,直线,射线,线段的定义,正确的作出图形是解题的关键.
20.
【分析】依据,,可得,再根据平分,即可得出,依据平角定义得到.
【详解】解:∵,
∴.
∵.
∴.
∵平分.
∴.
∴.
∵
∴.
【点睛】本题主要考查了垂线的意义,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
21.(1)30°
(2)45°
(3)60°
【分析】(1)由角平分线的定义,表示出,即可求解;
(2)由角平分线的定义,表示出,即可求解;
(3)由角平分线的定义,列出关于的方程组,即可求解.
【详解】(1)解:平分平分,
,,
,
.
(2)解:平分平分,
,
,
,
,
,
.
(3)解:平分,
,
,
,
,
,
,
,
.
【点睛】本题考查了角的计算,解题关键是由角平分线定义得出有关等式.
22.(1)见解析;(2)OF<OG;理由见解析;(3)∠AOD=70°,∠DOE=20°.
【分析】(1)使用量角器量出的度数,再用直角三角尺画它的平分线,使用直角三角尺画于G;
(2)根据垂线段最短即可确定OF和OG的大小;
(3)先利用邻补角计算出,再根据角平分线定义得,然后利用角互余计算的度数.
【详解】(1)先使用量角器量出的度数,再用直角三角尺画它的平分线;使用直角三角尺画于G,如下图所示,OD、FG即为所画
(2).理由如下:
是点O到FG的距离
由直线外一点与直线上各点的连线中,垂线段最短可知,;
(3)
∵OD是的平分线
∴
∵
∴
∴
故的度数为,的度数为.
【点睛】本题考查了角平分线和垂线的画法、垂线段最短、角互余等知识点,掌握角平分线的定义是解题关键.
23.(1)C
(2),
(3),理由见解析
【分析】(1)根据垂线段最短解答;
(2)根据周长公式计算即可;
(3)利用作差法比较大小.
【详解】(1)解:“”的理由是垂线段最短,
故选:C;
(2)解:;
(3)解:;
∵n∴n-m<0,
∴,
∴.
【点睛】此题考查了垂线的性质,计算图形的周长,利用作差法比较两个式子的大小,整式加减的应用,正确掌握垂线的性质及作差法比较大小的方法是解题的关键.
24.(1),
(2)或
(3)6秒或秒
【分析】(1)根据,,即可得出的度数,根据角平分线的定义得出,然后根据得出的度数;
(2)根据题意得出的度数,然后分两种情况进行讨论:①当射线在内部时;②当射线在外部时;分别进行计算即可;
(3)根据平分得出,根据题意画出图形,计算的角度,然后计算时间即可.
【详解】(1)解:由题意可知,,
∵,
∴,
∵平分,
∴,
∴;
(2)由(1)知,,
∴,
①当射线在内部时,如图2(1),
;
②当射线在外部时,如图2(2),
,
综上所述,的度数为或;
(3)∵平分,
∴,
①如图3,
,
∵平分,
∴,
∴,
∴旋转的时间(秒);
②如图3(1),
此时,,
∵平分,
∴,
∴,
∴,
∴旋转的时间(秒);
综上所述,旋转的时间为6秒或秒.
【点睛】本题主要考查角度的计算,角平分线的定义等内容;第(2)问进行合适的分类讨论是解题的关键;第(3)问,搞清楚在射线旋转的过程中,和的相对位置在不断的变化,以此进行分类画图.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.两条直线相交所成的四个角中,下列条件中能判定两条直线垂直的是( ).
A.有两个角相等 B.有两对角相等 C.有三个角相等 D.有四对邻补角
2.平面内,经过直线外一点画的垂线,能画出
A.1条 B.2条 C.3条 D.4条
3.在数学课上,同学们在练习过点B作线段AC所在直线的垂线段时,有一部分同学画出下列四种图形,正确的是( )
A. B. C.D.
4.如图,点A在直线l1上,点B,C在直线l2上,AB⊥l2,AC⊥l1,AB=4,BC=3,则下列说法正确的是( )
A.点A到直线l2的距离等于4
B.点C到直线l1的距离等于4
C.点C到AB的距离等于4
D.点B到AC的距离等于3
5.如图,在△ABC中,∠C=90,D是边BC上一点,且∠ADC=60,那么下列说法中错误的是( )
A.直线AD与直线BC的夹角为60 B.直线AC与直线BC的夹角为90
C.线段CD的长是点D到直线AC的距离 D.线段AB的长是点B到直线AD的距离
6.如图,已知直线,,则直线与重合,理由是( )
A.垂线段最短
B.在同一平面内,过一点有且只有一条直线与已知直线垂直
C.直线外一点到这条直线的垂线段的长度,叫做点到直线的距离
D.在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条
7.如图,,则的长度可能是( )
A.3 B.5 C.3或5 D.4.5
8.如图所示,点A到BC所在的直线的距离是指图中线段( )的长度.
A.AC B.AF C.BD D.CE
9.直线,相交于点.分别平分.下列说法正确的是( )
A.在同一直线上 B.在同一直线上
C. D.
10.如图,直线AB、CD相交于点O,OE⊥AB,O为垂足,如果∠EOD=38°,下列结论不正确的是( )
A.∠EOB=90° B.∠DOB是∠AOE 的补角
C.∠AOC=52° D.∠AOC与∠EOD 互为余角
二、填空题
11.如果∠,∠两边分别垂直,其中∠比∠的2倍少30°,那么∠= .
12.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠AOC:∠COE=2:3,则∠AOD= .
13.如图,直线AB、CD相交于点O,OE平分,于点O.若,则等于 .
14.点O为线段AB上一点,不与点A、B重合,OC⊥OD于点O,若∠AOC=35°,则∠BOD的度数为 .
15.如图,点C,O,D在一条直线上,,OE平分比大,的度数为 .
16.已知点O是直线上一点,,平分,,请写出下列正确结论的序号
①②③④
17.如图,直线,相交于点,,垂足为点.当直线绕着点在内部转动,是的角平分线,若,则,则关于的函数关系式为 .
18.100条直线两两相交于一点,则共有对顶角(不含平角) 对,邻补角 对.
三、解答题
19.如图,A、B、C是平面内三点.
(1)按要求作图:
①作射线BC,过点B作直线l,使A、C两点在直线l两旁;
②点P为直线l上任意一点,点Q为直线BC上任意一点,连接线段AP、PQ;
(2)在(1)所作图形中,若点A到直线l的距离为2,点A到直线BC的距离为5,点A、B之间的距离为8,点A、C之间的距离为6,则AP+PQ的最小值为__________,依据是__________
20.如图,直线、相交于点,平分,,,求的度数.
21.如图,已知是内三条射线,平分平分.
(1)若,求的度数.
(2)若,求的度数.
(3)若,求的度数.
22.如图,O为直线AB上一点,F为射线OC上一点,OE⊥AB.
(1)用量角器和直角三角尺画∠AOC的平分线OD,画FG⊥OC,FG交AB于点G;
(2)在(1)的条件下,比较OF与OG的大小,并说明理由;
(3)在(1)的条件下,若∠BOC=40°,求∠AOD与∠DOE的度数.
23.如图,用三张卡片拼成如下图①,图②所示的两个四边形,其周长分别为、.
(1)请你根据所学知识解释:在直角三角形卡片中,“”的理由是_________.(填写正确选项的字母)
A.两点之间线段最短;B.过一点有且只有一条直线与已知直线垂直;C.垂线段最短;D.两点确定一条直线.
(2)分别计算、(用含m、n的代数式表示);
(3)比较与的大小,并说明理由.
24.点O为直线l上一点,射线均与直线l重合,如图1所示,过点O作射线和射线,使得,,作的平分线.
(1)求与的度数;
(2)作射线,使得,请在图2中画出图形,并求出的度数;
(3)如图3,将射线从图1位置开始,绕点O以每秒的速度逆时针旋转一周,作的平分线,当时,求旋转的时间.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
【分析】两直线相交所成的四个角中,有一个角为90°,则这两条直线互相垂直,根据的定义判断即可.
【详解】解:A、两条直线相交成四个角,如果有两个角相等,是两个对顶角相等,那么这两条直线不一定垂直,故本选项错误;
B、两条直线相交成四个角,如果有两对角相等,是两对对顶角相等,那么这两条直线不一定垂直,故本选项错误;
C、两条直线相交成四个角,则这四个角中有2对对顶角.如果三个角相等,则这四个角相等,都是直角,所以这两条直线垂直.故正确;
D、两条直线相交成四个角,如果有四对邻补角,是四对普通的邻补角,那么这两条直线不一定垂直,故本选项错误;
故选:C.
【点睛】本题主要考查了垂线的定义,对顶角的定义,邻补角的定义,是基础题,熟记概念是解题的关键.
2.A
【分析】平面内经过一点有且只有一条直线垂直于已知直线,据此可得.
【详解】经过直线l外一点画l的垂线,能画出1条垂线,
故选A.
【点睛】本题主要考查垂线,解题的关键是掌握在平面内,过一点有且只有一条直线与已知直线垂直.
3.A
【分析】满足两个条件:①经过点B.②垂直AC;由此即可判断.
【详解】解:根据垂线段的定义可知,图①线段BE,是点B作线段AC所在直线的垂线段,
故选A.
【点睛】本题考查作图-复制作图,垂线的定义等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.
4.A
【分析】根据点到直线的距离的定义:直线外一点到这条直线的垂线段的长度,即可得到答案.
【详解】解:点A到直线l2的距离为AB的长,等于4,故A正确;
点C到直线l1的距离为AC的长,大于4,故B错误;
点C到AB的距离为BC的长,等于3,故C错误;
同理,点B到AC的距离也不是3,故D错误,
故选:A
【点睛】本题考查点到直线的距离,掌握定义是解题的关键.
5.D
【分析】根据已知角即可判断A、B;根据点到直线的距离的定义即可判断C、D.
【详解】解:A、∵∠CDA=60,
∴直线AD与直线BC的夹角是60,正确,故不符合题意;
B、∵∠ACD=90,
∴直线AC与直线BC的夹角是90,正确,故不符合题意;
C、∵∠ACD=90,
∴DC⊥AC,
∴线段CD的长是点D到直线AC的距离,正确,故不符合题意;
D、∵BD和AD不垂直,
∴线段AB的长不是点B到直线AD的距离,错误,故本选项符合题意;
故选:D.
【点睛】本题考查了点到直线的距离,以及直线与直线的夹角,注意:点到直线的距离是指该点到直线的垂线段的长.
6.B
【分析】直接利用垂线的性质进而分析得到答案.
【详解】∵,,垂足为B,
∴AB和BC重合,理由是:
在同一平面内,过一点有且只有一条直线与已知直线垂直.
故选:B.
【点睛】本题考查了同一平面内直线的垂直关系及垂线段的知识点,解题的关键是熟悉对垂线段定义的理解.
7.D
【分析】根据垂线段最短可得3<BD<5.
【详解】解:∵AD⊥BD,BC⊥CD,AB=5,BC=3,
∴BC<BD<AB,
即3<BD<5.
故选:D.
【点睛】此题主要考查了垂线段的性质,关键是掌握垂线段最短.
8.B
【分析】根据点到直线的距离是垂线段的长度,可得答案.
【详解】点A到线段BC所在直线的距离是线段AF的长度,
故选B.
【点睛】本题考查了点到直线的距离,利用点到直线的距离的定义是解题关键.
9.D
【分析】根据角平分线的性质得到,又因为与是补角,所以,所以,所以A错误,D正确;因为,且与是对顶角,所以,所以,与共线,所以,,所以B,C均错误.
【详解】解:如图,
∵,
∵分别是的平分线,
∴,
∵是的平分线,
∴,
∴,
∴,
∴射线互相垂直,故D正确;故A错误;射线互相垂直;故C错误;故B错误.
故选:D.
【点睛】本题考查了垂线,对顶角,角平分线的定义,正确的识别图形是解题的关键.
10.B
【分析】根据垂直的定义可知,故A正确;根据互补定义,由图知和互补,故B错误;根据OE⊥AB,∠EOD=38°,结合对顶角定义,可得,故C正确;根据互余定义和对顶角定义可知,即可得到∠AOC与∠EOD 互为余角,故D正确,从而得到结论.
【详解】解:A、由于OE⊥AB,则,故该选项不符合题意;
B、由于三点共线,则,即∠DOB是∠AOE 的补角错误,故该选项符合题意;
C、由于OE⊥AB,则,再结合∠EOD=38°,根据对顶角相等可知,故该选项不符合题意;
D、由于OE⊥AB,则,从而,根据对顶角相等可得,∠AOC与∠EOD 互为余角,故该选项不符合题意;
故选:B.
【点睛】本题考查垂线的定义、互余的定义、互补的定义和对顶角相等的性质等知识点,熟记概念,准确识图并找到各个相关角度之间的数量关系是解决问题的关键.
11.或
【分析】分两种情况,当时,当,然后进行计算即可解答,
【详解】解:设为,则,
分两种情况:
当时,如图:
,
解得:,
,
当,如图:
,
解得:,
综上所述:或.
故答案为:或.
【点睛】本题考查了垂线,角的计算,根据题意画出图形,分两种情况讨论是解题的关键.
12.144°
【分析】直接利用垂直的定义得出∠AOE=90°,进而利用∠AOC:∠COE=2:3,得出∠AOC的度数,进而得出答案.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
∵∠AOC:∠COE=2:3,
∴设∠AOC=2x,∠COE=3x,
则3x+2x=90°,
解得:x=18°,
故∠AOC=36°,
则∠AOD=180°-36°=144°.
故答案为:144°.
【点睛】此题主要考查了垂直的定义以及邻补角,正确得出∠AOC度数是解题关键.
13.##50度
【分析】根据对顶角相等可得,再根据角平分线的性质得,最后根据平角的性质求解即可.
【详解】解:∵,
∴.
∵OE 平分∠BOC,
∴.
∵OF⊥OE,
∴,
∴.
故答案为:.
【点睛】本题考查了角的度数问题、垂直定义以及角平分线的定义,掌握对顶角相等、平角的定义是解题的关键.
14.55°或125°
【分析】分OC,OD在AB的同侧和异侧两种情况求解.
【详解】当OC和OD在AB同一侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC=35°,
∴∠BOD=90°﹣∠AOC=90°﹣35°=55°,
当OC和OD在AB同异侧时,如图:
∵OC⊥OD,
∴∠COD=90°,
∵∠AOC=35°,
∴∠AOD=55°,
∴∠BOD=180°﹣∠AOD=180°﹣55°=125°.
∴∠BOD的度数为55°或125°.
故答案为:55°或125°.
【点睛】本题考查了垂直的定义即两直线相交,交成的四个角中有一个是直角,理解定义,学会分类是解题的关键.
15.##72.5度
【分析】根据比大,和互补,即可求出,进而由垂直性质可求出,再由角平分线性质即可得出答案.
【详解】解:∵比大,
∴设,则,
∵ ,
∴,
∴,
∴,
∵,
∴,
∴,
∴,
∵OE平分,
∴.
故答案为:.
【点睛】本题考查了垂直的性质,角平分线的性质以及角的运算,掌握以上知识是解题的关键.
16.①②③
【分析】根据图形的特点及角平分线的概念依次求出各角度即可解答.
【详解】解:∵,
∴∠BOC=180°-=130°,则①正确
∵OD平分,
∴∠AOD=,则②正确
∴∠BOD=180°-∠AOD=155°,则③正确
∵
∴∠COE=-=40°,则④错误.
故答案为:①②③.
【点睛】本题主要考查角平分线、垂直、邻补角的定义以及角的和差等知识点,熟知邻补角的定义及角平分线的定义成为解答本题的关键.
17.
【分析】先由角平分线定义得:,由垂直定义和角的和差,再根据,得到与的关系,进而得解.
【详解】∵是的角平分线,,
∴.
∵,
∴,
∵,
∴.
∵,
∴,
∴,
故答案是.
【点睛】本题主要考查垂直的定义,角平分线的定义,补角的定义,由,,推导出关于的函数关系式是解本题的关键.
18. 9900 19800
【分析】由特殊情况总结出一般规律,应用规律即可求解.
【详解】解:图①中共有2对对顶角,4对邻补角,
图②中共有6对对顶角,12对邻补角,
图③中共有12对对顶角,24对邻补角,
,
根据上面的规律,直线条数与对顶角对数之间的关系为:若有n条直线相交于一点,则可形成对对顶角.对邻补角,
若100条直线相交于一点,则可形成9900对对顶角,19800对邻补角,
故答案为:9900,19800.
【点睛】本题考查有规律性的数学问题,关键是由特殊情况总结出一般规律.
19.(1)①见解析;②见解析
(2)5,垂线段最短
【分析】(1)根据题意作出图形即可;
(2)根据线段的性质即可得到结论.
【详解】(1)解:①如图1所示,射线BC,直线l即为所求;
②如图1所示,线段AP,PQ即为所求;
;
(2)解:过A作AQ⊥BC交直线l于P,
则此时,AP+PQ的值最小,
∵点A到直线BC的距离为5,
∴AP+PQ的最小值为5,
依据是垂线段最短,
故答案为:5,垂线段最短.
【点睛】本题考查了点到直线的距离,直线,射线,线段的定义,正确的作出图形是解题的关键.
20.
【分析】依据,,可得,再根据平分,即可得出,依据平角定义得到.
【详解】解:∵,
∴.
∵.
∴.
∵平分.
∴.
∴.
∵
∴.
【点睛】本题主要考查了垂线的意义,角平分线的定义以及余角的综合运用,正确的识别图形是解题的关键.
21.(1)30°
(2)45°
(3)60°
【分析】(1)由角平分线的定义,表示出,即可求解;
(2)由角平分线的定义,表示出,即可求解;
(3)由角平分线的定义,列出关于的方程组,即可求解.
【详解】(1)解:平分平分,
,,
,
.
(2)解:平分平分,
,
,
,
,
,
.
(3)解:平分,
,
,
,
,
,
,
,
.
【点睛】本题考查了角的计算,解题关键是由角平分线定义得出有关等式.
22.(1)见解析;(2)OF<OG;理由见解析;(3)∠AOD=70°,∠DOE=20°.
【分析】(1)使用量角器量出的度数,再用直角三角尺画它的平分线,使用直角三角尺画于G;
(2)根据垂线段最短即可确定OF和OG的大小;
(3)先利用邻补角计算出,再根据角平分线定义得,然后利用角互余计算的度数.
【详解】(1)先使用量角器量出的度数,再用直角三角尺画它的平分线;使用直角三角尺画于G,如下图所示,OD、FG即为所画
(2).理由如下:
是点O到FG的距离
由直线外一点与直线上各点的连线中,垂线段最短可知,;
(3)
∵OD是的平分线
∴
∵
∴
∴
故的度数为,的度数为.
【点睛】本题考查了角平分线和垂线的画法、垂线段最短、角互余等知识点,掌握角平分线的定义是解题关键.
23.(1)C
(2),
(3),理由见解析
【分析】(1)根据垂线段最短解答;
(2)根据周长公式计算即可;
(3)利用作差法比较大小.
【详解】(1)解:“”的理由是垂线段最短,
故选:C;
(2)解:;
(3)解:;
∵n
∴,
∴.
【点睛】此题考查了垂线的性质,计算图形的周长,利用作差法比较两个式子的大小,整式加减的应用,正确掌握垂线的性质及作差法比较大小的方法是解题的关键.
24.(1),
(2)或
(3)6秒或秒
【分析】(1)根据,,即可得出的度数,根据角平分线的定义得出,然后根据得出的度数;
(2)根据题意得出的度数,然后分两种情况进行讨论:①当射线在内部时;②当射线在外部时;分别进行计算即可;
(3)根据平分得出,根据题意画出图形,计算的角度,然后计算时间即可.
【详解】(1)解:由题意可知,,
∵,
∴,
∵平分,
∴,
∴;
(2)由(1)知,,
∴,
①当射线在内部时,如图2(1),
;
②当射线在外部时,如图2(2),
,
综上所述,的度数为或;
(3)∵平分,
∴,
①如图3,
,
∵平分,
∴,
∴,
∴旋转的时间(秒);
②如图3(1),
此时,,
∵平分,
∴,
∴,
∴,
∴旋转的时间(秒);
综上所述,旋转的时间为6秒或秒.
【点睛】本题主要考查角度的计算,角平分线的定义等内容;第(2)问进行合适的分类讨论是解题的关键;第(3)问,搞清楚在射线旋转的过程中,和的相对位置在不断的变化,以此进行分类画图.
答案第1页,共2页
答案第1页,共2页
