泸教版七年级数学下学期期末专项复习 第十三章相交线平行线(基础卷)(含解析)
文档属性
| 名称 | 泸教版七年级数学下学期期末专项复习 第十三章相交线平行线(基础卷)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 399.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 11:46:07 | ||
图片预览



文档简介
第十三章 相交线 平行线(基础卷)-七年级数学下学期期末专项复习(沪教版)
第十三章 相交线 平行线(基础)
考试时间:120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.点A为直线a外一点,点B是直线a上一点,点A到直线a的距离为5cm,则AB的长度可能为( )
A.2cm B.3cm C.4cm D.18cm
2.点A为直线a外一点,点B是直线a上点,点A到直线a的距离为5,则AB的长度一定不是( )
A.10 B.8 C.5 D.3
3.如图,在三角形中,若,于点,则下列线段的长度可以表示为点到直线距离的是( )
A. B. C. D.
4.下列说法:①相等的角是对顶角;②同位角相等;③过一点有且只有一条直线与已知直线平行;④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;其中正确的有( )个.
A.0 B.1 C.2 D.3
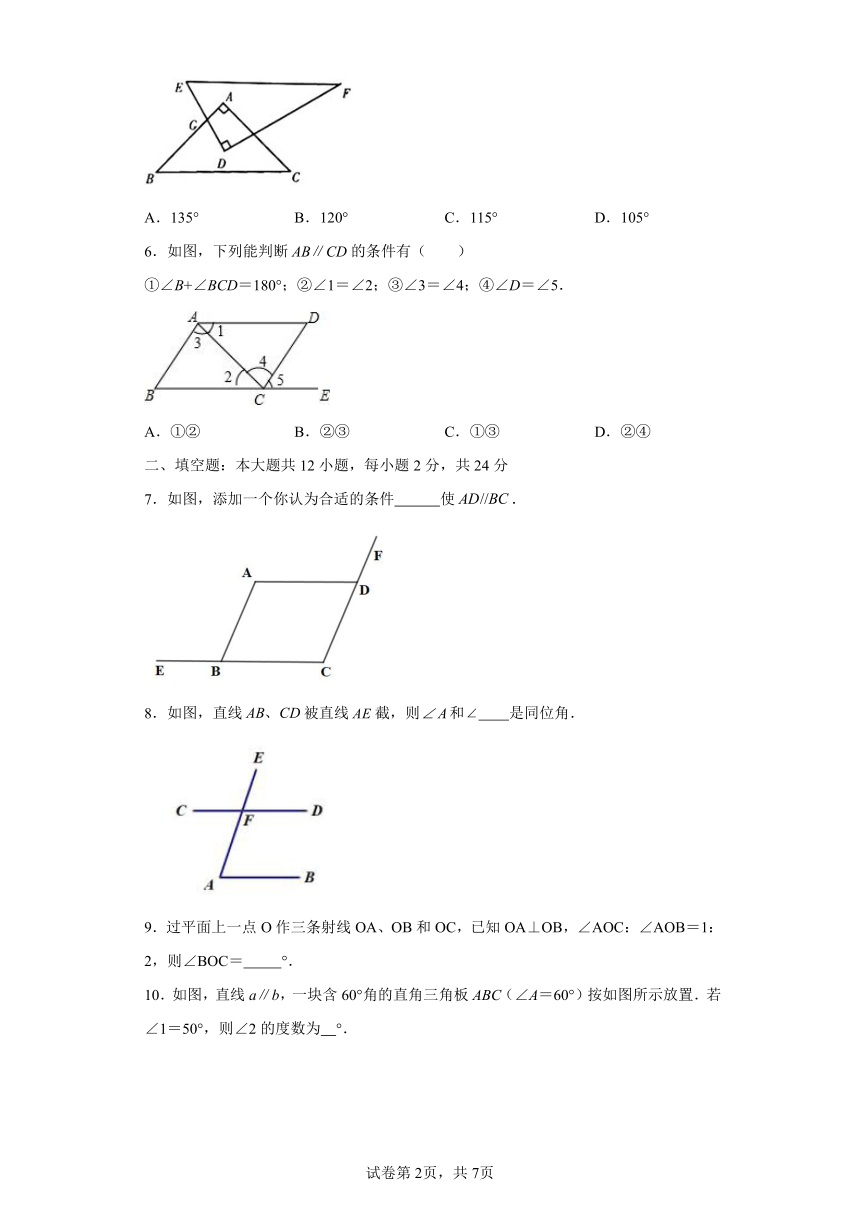
5.如图摆放的一副学生用直角三角板,,与相交于点G,当时,的度数是( )
A.135° B.120° C.115° D.105°
6.如图,下列能判断AB∥CD的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5.
A.①② B.②③ C.①③ D.②④
二、填空题:本大题共12小题,每小题2分,共24分
7.如图,添加一个你认为合适的条件 使.
8.如图,直线被直线截,则和 是同位角.
9.过平面上一点O作三条射线OA、OB和OC,已知OA⊥OB,∠AOC:∠AOB=1:2,则∠BOC= °.
10.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为 °.
11.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠AOB=50°,则∠ODE的度数是 .
12.如图所示,把长方形纸片ABCD纸沿对角线折叠,若∠BDE=20°,那么∠BED= .
13.如图,平分,若,则 .
14.如图,AB∥MN,点C在直线MN上,CB平分∠ACN,∠A=40°,则∠B的度数为 .
15.如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处,若∠AEH=30°,则∠EFC等于 °.
16.如图,三角形ABC中,D是AB上一点,F是BC上一点,E,H是AC上的点,EF的延长线交AB的延长线于点G,连接DE,DH,DE∥BC.若∠CEF=∠CHD,∠EFC=∠ADH,∠CEF:∠EFC=5:2,∠C=47°,则∠ADE的度数为 .
17.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
18.如图,C为∠AOB的边OA上一点,过点C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H,若∠EFD=α,现有以下结论:①∠COF=α;②∠AOH=180°﹣2α;③CH⊥CD;④∠OCH=2α﹣90°.其中正确的是 (填序号).
三、解答题:本大题共7小题,共58分
19.如图,直线AB,CD相交于点O.射线OF⊥CD于点O,∠BOF=30°,求∠BOD,∠AOD的度数.
20.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
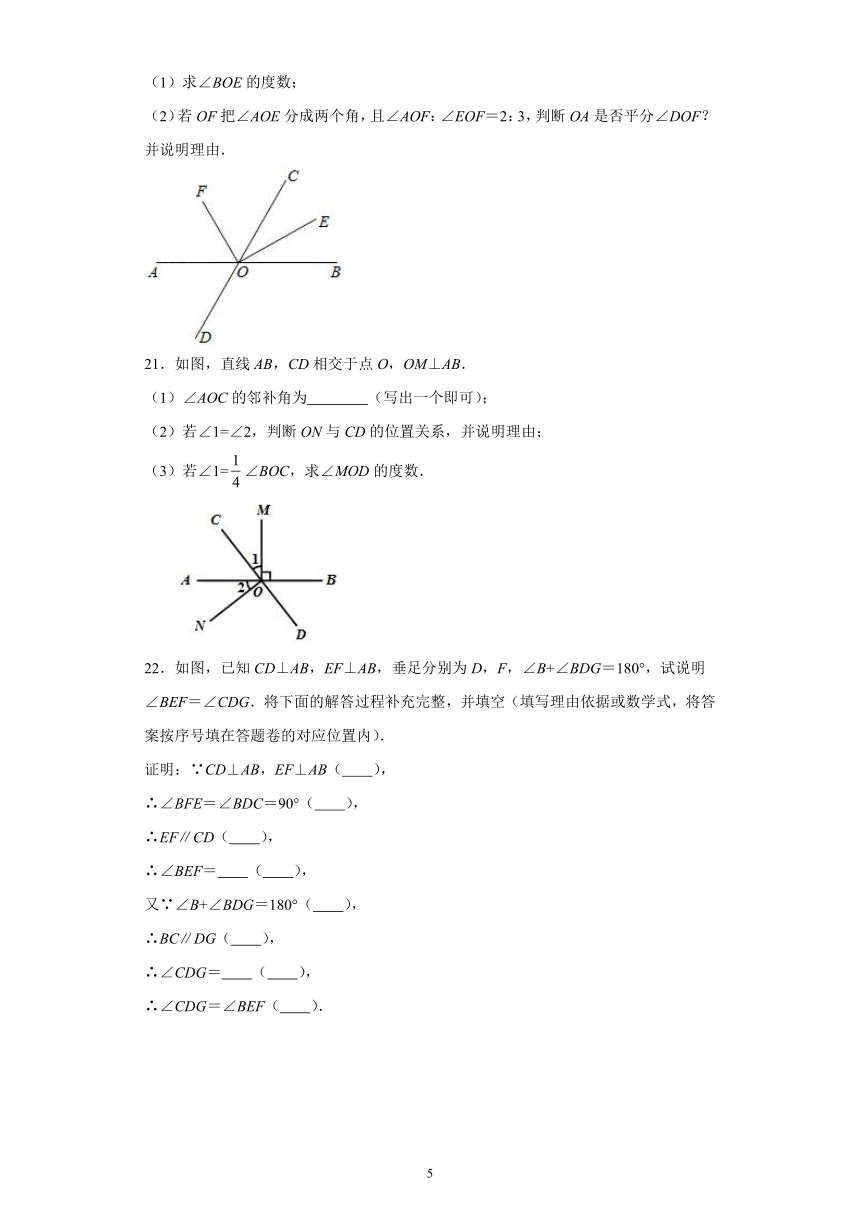
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
21.如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=∠BOC,求∠MOD的度数.
22.如图,已知CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°,试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式,将答案按序号填在答题卷的对应位置内).
证明:∵CD⊥AB,EF⊥AB( ),
∴∠BFE=∠BDC=90°( ),
∴EF∥CD( ),
∴∠BEF= ( ),
又∵∠B+∠BDG=180°( ),
∴BC∥DG( ),
∴∠CDG= ( ),
∴∠CDG=∠BEF( ).
23.中,,点P在BC边上运动(P不与B.C重合),连接AP,作,PQ交AB于点Q.
(1)如图1,当时,判断的形状并说明理由;
(2)在点P的运动过程中,的形状可以是等腰三角形吗?若可以,请直接写出的度数;若不可以,请说明理由.
24.已知:直线分别与直线,交于点,.平分,平分,并且.
(1)如图1,求证:;
(2)如图2,,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为.
25.已知,直线AB//CD,∠EFG=90°.
(1)如图1,点F在AB上,FG与CD交于点N,若∠EFB=65°,则∠FNC= °;
(2)如图2,点F在AB与CD之间,EF与AB交于点M,FG与CD交于点N.∠AMF的平分线MH与∠CNF的平分线NH交于点H.
①若∠EMB=α,求∠FNC(用含α的式子表示);
②求∠MHN的度数.
参考答案:
1.D
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
【详解】解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为5cm,
∴AB最短为5cm.
∴AB≥5cm,
∴AB的长度可能为18cm.
故选:D.
【点睛】本题主要考查了垂线段最短的应用,准确计算是解题的关键.
2.D
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
【详解】解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为5,
∴AB最短为5.
∴AB≥5,
∴AB的长度一定不是3.
故选:D.
【点睛】本题主要考查了垂线段最短,解答此题的关键是注意:从直线外一点到这条直线上各点所连的线段中,垂线段最短.
3.A
【分析】根据点到直线的距离的概念回答即可.
【详解】解:∵CD⊥AB于点D,
根据点到直线的距离的概念可知:
点A到直线CD距离的是线段AD的长,
故选A.
【点睛】本题考查了垂直的定义和点到直线的距离,属于基础题型,难度不大.
4.B
【分析】根据对顶角的性质即可判断①;根据同位角的定义和平行线的性质即可判断②;根据平行公理即可判断③;根据点到直线的距离的定义即可判断④.
【详解】解:①对顶角相等,但相等的角不一定是对顶角,故①错误;
②两直线平行,同位角相等,故②错误;
③过直线外一点有且只有一条直线与已知直线平行,故③错误;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故④正确.
故选:B.
【点睛】本题考查了对顶角的性质、同位角的定义、平行线的性质、平行公理、点到直线的距离的定义,解题的关键是熟练掌握相关知识点.
5.D
【分析】过点G作,则有,,又因为和都是特殊直角三角形,,可以得到,有即可得出答案.
【详解】解:过点G作,有,
∵在和中,
∴
∴,
∴
故的度数是105°.
【点睛】本题主要考查了平行线的性质和三角形内角和定理,其中平行线的性质为:两直线平行,内错角相等;三角形内角和定理为:三角形的内角和为180°;其中正确作出辅助线是解本题的关键.
6.C
【分析】根据题目中的条件,可以写出各个小题中的条件可以得到哪两条线平行,从而可以解答本题.
【详解】解:∵∠B+∠BCD=180°,
∴AB∥CD,故①符合题意;
∵∠1=∠2,
∴AD∥BC,故②不符合题意;
∵∠3=∠4,
∴AB∥CD,故③符合题意;
∵∠D=∠5,
∴AD∥BC,故④不符合题意;
故选:C.
【点睛】本题主要考查了平行线的判定,准确分析判断是解题的关键.
7.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
【分析】根据平行线的判定方法即可求解.
【详解】第一种情况,同位角相等,两直线平行,即∠ADF=∠C时,;
第二种情况,内错角相等,两直线平行,即∠A=∠ABE时,;
第三种情况,同旁内角互补,两直线平行,即∠A+∠ABC=180°或∠C+∠ADC=180°时,;
故答案为∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°.
【点睛】本题考查了平行线的判定方法,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
8.EFD
【分析】根据同位角的定义进行分析解答即可,两个角都在截线的同旁,又分别处在被截的两条直线同侧,具有这样位置关系的一对角叫做同位角.
【详解】直线被直线截,和EFD是同位角
故答案为:EFD.
【点睛】本题主要考查同位角的定义,关键在于运用相关的定义正确地进行分析.
9.135或45##45或135
【分析】根据题意画出图形,再结合垂直定义进行计算即可.
【详解】解:∵OA⊥OB,
∴∠AOB=90°,
∵∠AOC∶∠AOB=1∶2,
∴∠AOC=45°,
如图1:∠BOC=90°+45°=135°,
如图2:∠BOC=90°﹣45°=45°,
故答案为:135或45.
【点睛】此题主要考查了垂直的概念和角的计算,关键是根据题意画出图形,分情况分别求解.
10.110
【分析】根据三角形外角和内角的关系,先求出∠3的度数,再利用平行线的性质,求出∠2.
【详解】解:如图所示,∵∠1=∠ADE=50°,
∠3=∠A+∠ADE
=50°+60°
=110°.
∵a∥b,
∴∠2=∠3=110°.
故答案为:110°.
【点睛】本题主要考查了三角形内角和定理、外角定理和平行线的性质,准确计算是解题的关键.
11.25°
【分析】利用角平分线可得∠BOC=,然后利用平行线的性质可得答案.
【详解】解:∵OC平分∠AOB,∠AOB=50°,
∴∠BOC==25°,
∵ED∥OB,
∴∠EDO=∠DOB=25°,
故答案为:25°.
【点睛】本题主要考查了角平分线的定义和平行线的性质,准确计算是解题的关键.
12.140°
【分析】由AD∥BC,利用“两直线平行,内错角相等”可得出∠CBD的度数,由折叠的性质可得出∠EBD的度数,结合∠CBE=∠CBD+∠EBD可得出∠CBE的度数,由AD∥BC,利用“两直线平行,同旁内角互补”可求出∠BED的度数.
【详解】解:∵AD∥BC,
∴∠CBD=∠BDE=20°.
由折叠的性质可知:∠EBD=∠CBD=20°,
∴∠CBE=∠CBD+∠EBD=40°.
∵AD∥BC,
∴∠BED=180°﹣∠CBE=140°.
故答案为:140°.
【点睛】本题考查了平行线的性质以及折叠的性质,牢记“两直线平行,同旁内角互补”是解题的关键.
13.65
【分析】利用平行线的判定定理和性质定理,等量代换可得∠CBD=∠EBC,可得结果.
【详解】∵∠1=50°,
∴∠DBE=180°-∠1=180°-50°=130°,
∵∠2=130°,
∴∠DBE=∠2,
∴AE∥CF,
∴∠4=∠ADF,
∵∠3=∠4,
∴∠EBC=∠4,
∴AD∥BC,
∵AD平分∠BDF,
∴∠ADB=∠ADF,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠4=∠CBD,
∴∠CBD=∠EBC=∠DBE=×130°=65°.
故答案为:65.
【点睛】本题主要考查了平行线的判定定理和性质定理,角平分线的定义等,熟练掌握定理是解答此题的关键.
14.70°
【分析】先由AB∥MN知∠A+∠ACN=180°,结合∠A度数得出∠ACN的度数,再由CB平分∠ACN知∠ACB=∠ACN=70°,最后根据三角形内角和定理可得答案.
【详解】解:∵AB∥MN,
∴∠A+∠ACN=180°,
又∵∠A=40°,
∴∠ACN=180°﹣∠A=140°,
∵CB平分∠ACN,
∴∠ACB=∠ACN=70°,
∴∠B=180°﹣∠A﹣∠ACB=70°,
故答案为:70°.
【点睛】本题主要考查了与平行线有关的三角形内角和问题,结合角平分线的性质求解是解题的关键.
15.105
【分析】根据折叠得出∠DEF=∠HEF,求出∠DEF的度数,根据平行线的性质得出∠DEF+∠EFC=180°,代入求出即可.
【详解】解:∵将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处,
∴∠DEF=∠HEF,
∵∠AEH=30°,
∴∠DEF=∠HEF=(180°﹣∠AEH)=75°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠EFC=180°﹣75°=105°,
故答案为:105.
【点睛】本题主要考查了折叠的性质和平行线的性质应用,准确计算是解题的关键.
16.76°
【分析】根据平行线的性质和三角形的内角和解答即可.
【详解】解:∵∠CEF=∠CHD,
∴DH∥GE,
∴∠ADH=∠G,
∵∠EFC=∠ADH,
∵∠BFG=∠EFC,
∴∠G=∠BFG,
∴∠ABC=∠G+∠BFG=2∠EFC,
∵∠CEF:∠EFC=5:2,∠C=47°,
∴∠EFC=38°,
∴∠ABC=76°,
∵DE∥BC,
∴∠ADE=∠ABC=76°,
故答案为:76°.
【点睛】本题主要考查了平行线的性质和三角形内角和定理,准确计算是解题的关键.
17.59或121
【分析】分两种情况:①当射线GP⊥EG于点G时,∠PGE=90°,②当射线GP′⊥EG于点G时,∠P′GE=90°,根据平行线的判定与性质和角平分线定义即可求出∠PGF的度数.
【详解】解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF==31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
【点睛】本题主要考查了平行线的性质和角平分线的定义,准确计算是解题的关键.
18.①②③④
【分析】分别根据平行线的性质,角平分线的定义,邻补角的定义,直角三角形两锐角互余进行判断即可得出结论.
【详解】解:∵CD∥OB,∠EFD=α,
∴∠EOB=∠EFD=α,
∵OE平分∠AOB,
∴∠COF=∠EOB=α,故①正确;
∠AOB=2α,
∵∠AOB+∠AOH=180°,
∴∠AOH=180°﹣2α,故②正确;
∵CD∥OB,CH⊥OB,
∴CH⊥CD,故③正确;
∴∠HCO+∠HOC=90°,∠AOB+∠HOC=180°,
∴∠OCH=2α﹣90°,故④正确.
故答案为:①②③④.
【点睛】本题考查了平行线的性质,角平分线的定义,邻补角的定义,直角三角形两锐角互余等知识,熟练掌握相关知识点是解题关键.
19.60°,120°
【分析】利用垂线定义可得∠DOF=90°,再结合条件∠BOF=30°,可求出∠BOD的度数,利用邻补角互补可得∠AOD的度数.
【详解】∵OF⊥CD,
∴∠DOF=90°,
∵∠BOF=30°,
∴∠BOD=∠DOF-∠BOF=90°-30°=60°,
∵∠AOD+ ∠BOD= 180° ,
∴∠AOD=180°-∠BOD= 180°-60°=120°.
【点睛】本题主要考查了垂线,关键是掌握垂线定义,掌握邻补角互补.
20.(1)30°;(2)平分,理由见解析.
【分析】(1)根据邻补角的概念求出,根据角平分线的定义计算,得到答案;
(2)求出,根据题意分别求出,根据角平分线的定义证明即可.
【详解】解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
【点睛】本题考查的是对顶角、角平分线的定义、邻补角的概念,掌握对顶角相等、角平分线的定义是解题的关键.
21.(1)∠BOC,∠AOD;(2)ON⊥CD.证明见解析;(3)150°.
【分析】(1)利用直线CD或直线AB直接写∠AOC的邻补角,
(2)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,
再利用等量代换可得到∠2+∠AOC=90°,从而可得答案;
(3)根据垂直定义和条件可得∠1=30°,再根据邻补角定义可得∠MOD的度数.
【详解】解:(1)∠AOC+∠BOC=180°,
故答案为:∠BOC.(答案不唯一)
(2)结论:ON⊥CD.
证明:∵OM⊥AB,
∴∠1+∠AOC=90°.
又∵∠1=∠2,
∴∠NOC=∠2+∠AOC=90°,
∴ON⊥CD.
(3)∵∠1=∠BOC,
∴∠BOC=4∠1.
∵∠BOC-∠1=∠MOB=90°,
∴∠1=30°,
∴∠MOD=180°-∠1=150°.
【点睛】本题考查的是邻补角的定义及性质,角的和差计算,垂线的定义及性质,掌握以上知识是解题关键.
22.已知;垂直定义;同位角相等,两直线平行;∠BCD;两直线平行,同位角相等;已知;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;等量代换
【分析】根据平行线的判定与性质即可完成证明过程.
【详解】证明:∵CD⊥AB,EF⊥AB(已知),
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换).
故答案为:已知;垂直定义;同位角相等,两直线平行;∠BCD,两直线平行,同位角相等;已知,同旁内角互补,两直线平行;∠BCD,两直线平行,内错角相等;等量代换.
【点睛】本题主要考查了平行线的判定与性质应用,准确判断是解题的关键.
23.(1)是直角三角形,理由见详解;(2)的形状可以是等腰三角形,的度数为60°或105°
【分析】(1)先由等腰三角形的性质得∠C=∠B=30°,则∠BAC=120°,再由平行线的性质得∠PAC=∠APQ=30°,进而求出∠BAP=90°,即可;
(2)分三种情况,由等腰三角形的性质分别求出的度数即可.
【详解】(1)是直角三角形,理由如下:
∵,,
∴∠C=∠B=30°,
∴∠BAC=180°-30°-30°=120°,
∵,=30°,
∴∠PAC=∠APQ=30°,
∴∠BAP=120°-30°=90°,
∴是直角三角形;
(2)的形状可以是等腰三角形,理由如下:
①当QA=QP时,∠QAP=∠QPA=30°,
∴=∠QAP+∠QPA=60°,
②当PA=PQ时,∠PQA=,
∴=180°-75°=105°,
③当AQ=AP时,∠AQP=∠APQ=30°,
∴∠QAP=120°=∠BAC,即点P与点C重合,不符合题意,
综上所述,的度数为60°或105°.
【点睛】本题主要考查直角三角形的判定定理,等腰三角形的性质定理,熟练掌握等腰三角形的性质定理以及分类讨论思想,是解题的关键.
24.(1)见解析;(2),,,
【分析】(1)根据平行线的性质和判定可以解答;
(2)由已知及(1)的结论可知∠CFN=45°,然后结合图形根据角度的加减运算可以得到解答.
【详解】(1)证明:∵,∴.
∵平分,平分,∴,.
∴.
∴.
(2)由(1)知ABCD,
∴∠AEF+∠CFE=180°,
∵∠AEF=2∠CFN=∠CFE,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=∠FEM=∠BEM=45°,∠BEG=∠CFH=∠DFE=90°,
∴∠AEM=∠GEM=∠HFN=∠DFN=90°+45°=135°,
∴度数为135°的角有:、 、 、 .
【点睛】本题考查平行线的判定和性质及角平分线的综合运用,熟练掌握平行线的判定和性质定理及角平分线的意义是解题关键.
25.(1)25;(2)①∠FNC=90°﹣α;②45°.
【分析】(1)根据平行线的性质和互余解答即可;
(2)①过F作FP//AB,根据平行线的性质解答即可;
②过F作FQ//AB,根据平行线的性质解答即可.
【详解】(1)∵∠EFG=90°,∠EFB=65°,
∴∠BFD=90°﹣65°=25°,
∵AB//CD,
∴∠FNC=∠BFD=25°,
故答案为:25;
(2)①如图,过F作FP//AB,连接EG,
∵AB//CD,
∴AB//CD//FP,
∴∠MFP=∠EMB=α,
又∵∠EFG=90°,
∴∠PFN=90°﹣α,
∵FP//CD,
∴∠FNC=∠PFN=90°﹣α;
②如图,过F作FQ//AB,
∵AB//CD,
∴AB//CD//FQ,
∴∠MFQ=∠AMF,∠QFN=∠CNF,
∴∠AMF+∠CNF=∠MFQ+∠QFN=∠EFG=90°,
过H作HR//AB,
∵AB//CD,
∴AB//CD//HR,
∴∠AMH=∠MHR,∠HNC=∠NHR,
又∵MH平分∠AMF,NH平分∠CNF,
∴∠AMH=∠AMF,∠HNC=∠CNF,
∴∠MHN=∠MHR+∠NHR=∠AMH+∠HNC=(∠AMF+∠CNF)=×90°=45°.
【点睛】本题考查平行线的性质、角平分线的性质、角的和差等知识,是重要考点,难度较易,掌握相关知识是解题关键.
第十三章 相交线 平行线(基础)
考试时间:120分钟
注意事项:
1.答卷前,考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共6小题,每小题3分,共18分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.点A为直线a外一点,点B是直线a上一点,点A到直线a的距离为5cm,则AB的长度可能为( )
A.2cm B.3cm C.4cm D.18cm
2.点A为直线a外一点,点B是直线a上点,点A到直线a的距离为5,则AB的长度一定不是( )
A.10 B.8 C.5 D.3
3.如图,在三角形中,若,于点,则下列线段的长度可以表示为点到直线距离的是( )
A. B. C. D.
4.下列说法:①相等的角是对顶角;②同位角相等;③过一点有且只有一条直线与已知直线平行;④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离;其中正确的有( )个.
A.0 B.1 C.2 D.3
5.如图摆放的一副学生用直角三角板,,与相交于点G,当时,的度数是( )
A.135° B.120° C.115° D.105°
6.如图,下列能判断AB∥CD的条件有( )
①∠B+∠BCD=180°;②∠1=∠2;③∠3=∠4;④∠D=∠5.
A.①② B.②③ C.①③ D.②④
二、填空题:本大题共12小题,每小题2分,共24分
7.如图,添加一个你认为合适的条件 使.
8.如图,直线被直线截,则和 是同位角.
9.过平面上一点O作三条射线OA、OB和OC,已知OA⊥OB,∠AOC:∠AOB=1:2,则∠BOC= °.
10.如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=50°,则∠2的度数为 °.
11.如图,点D在∠AOB的平分线OC上,点E在OA上,ED∥OB,∠AOB=50°,则∠ODE的度数是 .
12.如图所示,把长方形纸片ABCD纸沿对角线折叠,若∠BDE=20°,那么∠BED= .
13.如图,平分,若,则 .
14.如图,AB∥MN,点C在直线MN上,CB平分∠ACN,∠A=40°,则∠B的度数为 .
15.如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处,若∠AEH=30°,则∠EFC等于 °.
16.如图,三角形ABC中,D是AB上一点,F是BC上一点,E,H是AC上的点,EF的延长线交AB的延长线于点G,连接DE,DH,DE∥BC.若∠CEF=∠CHD,∠EFC=∠ADH,∠CEF:∠EFC=5:2,∠C=47°,则∠ADE的度数为 .
17.如图,直线MN分别与直线AB,CD相交于点E,F,EG平分∠BEF,交直线CD于点G,若∠MFD=∠BEF=62°,射线GP⊥EG于点G,则∠PGF的度数为 度.
18.如图,C为∠AOB的边OA上一点,过点C作CD∥OB交∠AOB的平分线OE于点F,作CH⊥OB交BO的延长线于点H,若∠EFD=α,现有以下结论:①∠COF=α;②∠AOH=180°﹣2α;③CH⊥CD;④∠OCH=2α﹣90°.其中正确的是 (填序号).
三、解答题:本大题共7小题,共58分
19.如图,直线AB,CD相交于点O.射线OF⊥CD于点O,∠BOF=30°,求∠BOD,∠AOD的度数.
20.如图,直线AB,CD相交于点O,∠AOC=120°,OE平分∠BOC.
(1)求∠BOE的度数;
(2)若OF把∠AOE分成两个角,且∠AOF:∠EOF=2:3,判断OA是否平分∠DOF?并说明理由.
21.如图,直线AB,CD相交于点O,OM⊥AB.
(1)∠AOC的邻补角为 (写出一个即可);
(2)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(3)若∠1=∠BOC,求∠MOD的度数.
22.如图,已知CD⊥AB,EF⊥AB,垂足分别为D,F,∠B+∠BDG=180°,试说明∠BEF=∠CDG.将下面的解答过程补充完整,并填空(填写理由依据或数学式,将答案按序号填在答题卷的对应位置内).
证明:∵CD⊥AB,EF⊥AB( ),
∴∠BFE=∠BDC=90°( ),
∴EF∥CD( ),
∴∠BEF= ( ),
又∵∠B+∠BDG=180°( ),
∴BC∥DG( ),
∴∠CDG= ( ),
∴∠CDG=∠BEF( ).
23.中,,点P在BC边上运动(P不与B.C重合),连接AP,作,PQ交AB于点Q.
(1)如图1,当时,判断的形状并说明理由;
(2)在点P的运动过程中,的形状可以是等腰三角形吗?若可以,请直接写出的度数;若不可以,请说明理由.
24.已知:直线分别与直线,交于点,.平分,平分,并且.
(1)如图1,求证:;
(2)如图2,,在不添加任何辅助线的情况下,请直接写出图2中四个角,使写出的每个角的度数都为.
25.已知,直线AB//CD,∠EFG=90°.
(1)如图1,点F在AB上,FG与CD交于点N,若∠EFB=65°,则∠FNC= °;
(2)如图2,点F在AB与CD之间,EF与AB交于点M,FG与CD交于点N.∠AMF的平分线MH与∠CNF的平分线NH交于点H.
①若∠EMB=α,求∠FNC(用含α的式子表示);
②求∠MHN的度数.
参考答案:
1.D
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
【详解】解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为5cm,
∴AB最短为5cm.
∴AB≥5cm,
∴AB的长度可能为18cm.
故选:D.
【点睛】本题主要考查了垂线段最短的应用,准确计算是解题的关键.
2.D
【分析】垂线段最短指的是从直线外一点到这条直线所作的垂线段最短.它是相对于这点与直线上其他各点的连线而言.
【详解】解:∵A为直线a外一点,B是直线a上一点,点A到直线a的距离为5,
∴AB最短为5.
∴AB≥5,
∴AB的长度一定不是3.
故选:D.
【点睛】本题主要考查了垂线段最短,解答此题的关键是注意:从直线外一点到这条直线上各点所连的线段中,垂线段最短.
3.A
【分析】根据点到直线的距离的概念回答即可.
【详解】解:∵CD⊥AB于点D,
根据点到直线的距离的概念可知:
点A到直线CD距离的是线段AD的长,
故选A.
【点睛】本题考查了垂直的定义和点到直线的距离,属于基础题型,难度不大.
4.B
【分析】根据对顶角的性质即可判断①;根据同位角的定义和平行线的性质即可判断②;根据平行公理即可判断③;根据点到直线的距离的定义即可判断④.
【详解】解:①对顶角相等,但相等的角不一定是对顶角,故①错误;
②两直线平行,同位角相等,故②错误;
③过直线外一点有且只有一条直线与已知直线平行,故③错误;
④直线外一点到这条直线的垂线段的长度,叫做点到直线的距离,故④正确.
故选:B.
【点睛】本题考查了对顶角的性质、同位角的定义、平行线的性质、平行公理、点到直线的距离的定义,解题的关键是熟练掌握相关知识点.
5.D
【分析】过点G作,则有,,又因为和都是特殊直角三角形,,可以得到,有即可得出答案.
【详解】解:过点G作,有,
∵在和中,
∴
∴,
∴
故的度数是105°.
【点睛】本题主要考查了平行线的性质和三角形内角和定理,其中平行线的性质为:两直线平行,内错角相等;三角形内角和定理为:三角形的内角和为180°;其中正确作出辅助线是解本题的关键.
6.C
【分析】根据题目中的条件,可以写出各个小题中的条件可以得到哪两条线平行,从而可以解答本题.
【详解】解:∵∠B+∠BCD=180°,
∴AB∥CD,故①符合题意;
∵∠1=∠2,
∴AD∥BC,故②不符合题意;
∵∠3=∠4,
∴AB∥CD,故③符合题意;
∵∠D=∠5,
∴AD∥BC,故④不符合题意;
故选:C.
【点睛】本题主要考查了平行线的判定,准确分析判断是解题的关键.
7.∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°(答案不唯一,写一个正确的即可)
【分析】根据平行线的判定方法即可求解.
【详解】第一种情况,同位角相等,两直线平行,即∠ADF=∠C时,;
第二种情况,内错角相等,两直线平行,即∠A=∠ABE时,;
第三种情况,同旁内角互补,两直线平行,即∠A+∠ABC=180°或∠C+∠ADC=180°时,;
故答案为∠ADF=∠C或∠A=∠ABE或∠A+∠ABC=180°或∠C+∠ADC=180°.
【点睛】本题考查了平行线的判定方法,同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
8.EFD
【分析】根据同位角的定义进行分析解答即可,两个角都在截线的同旁,又分别处在被截的两条直线同侧,具有这样位置关系的一对角叫做同位角.
【详解】直线被直线截,和EFD是同位角
故答案为:EFD.
【点睛】本题主要考查同位角的定义,关键在于运用相关的定义正确地进行分析.
9.135或45##45或135
【分析】根据题意画出图形,再结合垂直定义进行计算即可.
【详解】解:∵OA⊥OB,
∴∠AOB=90°,
∵∠AOC∶∠AOB=1∶2,
∴∠AOC=45°,
如图1:∠BOC=90°+45°=135°,
如图2:∠BOC=90°﹣45°=45°,
故答案为:135或45.
【点睛】此题主要考查了垂直的概念和角的计算,关键是根据题意画出图形,分情况分别求解.
10.110
【分析】根据三角形外角和内角的关系,先求出∠3的度数,再利用平行线的性质,求出∠2.
【详解】解:如图所示,∵∠1=∠ADE=50°,
∠3=∠A+∠ADE
=50°+60°
=110°.
∵a∥b,
∴∠2=∠3=110°.
故答案为:110°.
【点睛】本题主要考查了三角形内角和定理、外角定理和平行线的性质,准确计算是解题的关键.
11.25°
【分析】利用角平分线可得∠BOC=,然后利用平行线的性质可得答案.
【详解】解:∵OC平分∠AOB,∠AOB=50°,
∴∠BOC==25°,
∵ED∥OB,
∴∠EDO=∠DOB=25°,
故答案为:25°.
【点睛】本题主要考查了角平分线的定义和平行线的性质,准确计算是解题的关键.
12.140°
【分析】由AD∥BC,利用“两直线平行,内错角相等”可得出∠CBD的度数,由折叠的性质可得出∠EBD的度数,结合∠CBE=∠CBD+∠EBD可得出∠CBE的度数,由AD∥BC,利用“两直线平行,同旁内角互补”可求出∠BED的度数.
【详解】解:∵AD∥BC,
∴∠CBD=∠BDE=20°.
由折叠的性质可知:∠EBD=∠CBD=20°,
∴∠CBE=∠CBD+∠EBD=40°.
∵AD∥BC,
∴∠BED=180°﹣∠CBE=140°.
故答案为:140°.
【点睛】本题考查了平行线的性质以及折叠的性质,牢记“两直线平行,同旁内角互补”是解题的关键.
13.65
【分析】利用平行线的判定定理和性质定理,等量代换可得∠CBD=∠EBC,可得结果.
【详解】∵∠1=50°,
∴∠DBE=180°-∠1=180°-50°=130°,
∵∠2=130°,
∴∠DBE=∠2,
∴AE∥CF,
∴∠4=∠ADF,
∵∠3=∠4,
∴∠EBC=∠4,
∴AD∥BC,
∵AD平分∠BDF,
∴∠ADB=∠ADF,
∵AD∥BC,
∴∠ADB=∠CBD,
∴∠4=∠CBD,
∴∠CBD=∠EBC=∠DBE=×130°=65°.
故答案为:65.
【点睛】本题主要考查了平行线的判定定理和性质定理,角平分线的定义等,熟练掌握定理是解答此题的关键.
14.70°
【分析】先由AB∥MN知∠A+∠ACN=180°,结合∠A度数得出∠ACN的度数,再由CB平分∠ACN知∠ACB=∠ACN=70°,最后根据三角形内角和定理可得答案.
【详解】解:∵AB∥MN,
∴∠A+∠ACN=180°,
又∵∠A=40°,
∴∠ACN=180°﹣∠A=140°,
∵CB平分∠ACN,
∴∠ACB=∠ACN=70°,
∴∠B=180°﹣∠A﹣∠ACB=70°,
故答案为:70°.
【点睛】本题主要考查了与平行线有关的三角形内角和问题,结合角平分线的性质求解是解题的关键.
15.105
【分析】根据折叠得出∠DEF=∠HEF,求出∠DEF的度数,根据平行线的性质得出∠DEF+∠EFC=180°,代入求出即可.
【详解】解:∵将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处,
∴∠DEF=∠HEF,
∵∠AEH=30°,
∴∠DEF=∠HEF=(180°﹣∠AEH)=75°,
∵四边形ABCD是长方形,
∴AD∥BC,
∴∠DEF+∠EFC=180°,
∴∠EFC=180°﹣75°=105°,
故答案为:105.
【点睛】本题主要考查了折叠的性质和平行线的性质应用,准确计算是解题的关键.
16.76°
【分析】根据平行线的性质和三角形的内角和解答即可.
【详解】解:∵∠CEF=∠CHD,
∴DH∥GE,
∴∠ADH=∠G,
∵∠EFC=∠ADH,
∵∠BFG=∠EFC,
∴∠G=∠BFG,
∴∠ABC=∠G+∠BFG=2∠EFC,
∵∠CEF:∠EFC=5:2,∠C=47°,
∴∠EFC=38°,
∴∠ABC=76°,
∵DE∥BC,
∴∠ADE=∠ABC=76°,
故答案为:76°.
【点睛】本题主要考查了平行线的性质和三角形内角和定理,准确计算是解题的关键.
17.59或121
【分析】分两种情况:①当射线GP⊥EG于点G时,∠PGE=90°,②当射线GP′⊥EG于点G时,∠P′GE=90°,根据平行线的判定与性质和角平分线定义即可求出∠PGF的度数.
【详解】解:如图,①当射线GP⊥EG于点G时,∠PGE=90°,
∵∠MFD=∠BEF=62°,
∴CD∥AB,
∴∠GEB=∠FGE,
∵EG平分∠BEF,
∴∠GEB=∠GEF==31°,
∴∠FGE=31°,
∴∠PGF=∠PGE﹣∠FGE=90°﹣31°=59°;
②当射线GP′⊥EG于点G时,∠P′GE=90°,
同理:∠P′GF=∠PGE+∠FGE=90°+31°=121°.
则∠PGF的度数为59或121度.
故答案为:59或121.
【点睛】本题主要考查了平行线的性质和角平分线的定义,准确计算是解题的关键.
18.①②③④
【分析】分别根据平行线的性质,角平分线的定义,邻补角的定义,直角三角形两锐角互余进行判断即可得出结论.
【详解】解:∵CD∥OB,∠EFD=α,
∴∠EOB=∠EFD=α,
∵OE平分∠AOB,
∴∠COF=∠EOB=α,故①正确;
∠AOB=2α,
∵∠AOB+∠AOH=180°,
∴∠AOH=180°﹣2α,故②正确;
∵CD∥OB,CH⊥OB,
∴CH⊥CD,故③正确;
∴∠HCO+∠HOC=90°,∠AOB+∠HOC=180°,
∴∠OCH=2α﹣90°,故④正确.
故答案为:①②③④.
【点睛】本题考查了平行线的性质,角平分线的定义,邻补角的定义,直角三角形两锐角互余等知识,熟练掌握相关知识点是解题关键.
19.60°,120°
【分析】利用垂线定义可得∠DOF=90°,再结合条件∠BOF=30°,可求出∠BOD的度数,利用邻补角互补可得∠AOD的度数.
【详解】∵OF⊥CD,
∴∠DOF=90°,
∵∠BOF=30°,
∴∠BOD=∠DOF-∠BOF=90°-30°=60°,
∵∠AOD+ ∠BOD= 180° ,
∴∠AOD=180°-∠BOD= 180°-60°=120°.
【点睛】本题主要考查了垂线,关键是掌握垂线定义,掌握邻补角互补.
20.(1)30°;(2)平分,理由见解析.
【分析】(1)根据邻补角的概念求出,根据角平分线的定义计算,得到答案;
(2)求出,根据题意分别求出,根据角平分线的定义证明即可.
【详解】解:(1)∵∠AOC=120°,
∴∠BOC=180°﹣120°=60°,
∵OE平分∠BOC,
∴∠BOE=∠BOC=×60°=30°;
(2)OA平分∠DOF,
理由如下:∵∠BOE=30°,
∴∠AOE=180°﹣30°=150°,
∵∠AOF:∠EOF=2:3,
∴∠AOF=60°,∠EOF=90°,
∵∠AOD=∠BOC=60°,
∴∠AOD=∠AOF,
∴OA平分∠DOF.
【点睛】本题考查的是对顶角、角平分线的定义、邻补角的概念,掌握对顶角相等、角平分线的定义是解题的关键.
21.(1)∠BOC,∠AOD;(2)ON⊥CD.证明见解析;(3)150°.
【分析】(1)利用直线CD或直线AB直接写∠AOC的邻补角,
(2)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,
再利用等量代换可得到∠2+∠AOC=90°,从而可得答案;
(3)根据垂直定义和条件可得∠1=30°,再根据邻补角定义可得∠MOD的度数.
【详解】解:(1)∠AOC+∠BOC=180°,
故答案为:∠BOC.(答案不唯一)
(2)结论:ON⊥CD.
证明:∵OM⊥AB,
∴∠1+∠AOC=90°.
又∵∠1=∠2,
∴∠NOC=∠2+∠AOC=90°,
∴ON⊥CD.
(3)∵∠1=∠BOC,
∴∠BOC=4∠1.
∵∠BOC-∠1=∠MOB=90°,
∴∠1=30°,
∴∠MOD=180°-∠1=150°.
【点睛】本题考查的是邻补角的定义及性质,角的和差计算,垂线的定义及性质,掌握以上知识是解题关键.
22.已知;垂直定义;同位角相等,两直线平行;∠BCD;两直线平行,同位角相等;已知;同旁内角互补,两直线平行;∠BCD;两直线平行,内错角相等;等量代换
【分析】根据平行线的判定与性质即可完成证明过程.
【详解】证明:∵CD⊥AB,EF⊥AB(已知),
∴∠BFE=∠BDC=90°(垂直定义),
∴EF∥CD(同位角相等,两直线平行),
∴∠BEF=∠BCD(两直线平行,同位角相等),
又∵∠B+∠BDG=180°(已知),
∴BC∥DG(同旁内角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠CDG=∠BEF(等量代换).
故答案为:已知;垂直定义;同位角相等,两直线平行;∠BCD,两直线平行,同位角相等;已知,同旁内角互补,两直线平行;∠BCD,两直线平行,内错角相等;等量代换.
【点睛】本题主要考查了平行线的判定与性质应用,准确判断是解题的关键.
23.(1)是直角三角形,理由见详解;(2)的形状可以是等腰三角形,的度数为60°或105°
【分析】(1)先由等腰三角形的性质得∠C=∠B=30°,则∠BAC=120°,再由平行线的性质得∠PAC=∠APQ=30°,进而求出∠BAP=90°,即可;
(2)分三种情况,由等腰三角形的性质分别求出的度数即可.
【详解】(1)是直角三角形,理由如下:
∵,,
∴∠C=∠B=30°,
∴∠BAC=180°-30°-30°=120°,
∵,=30°,
∴∠PAC=∠APQ=30°,
∴∠BAP=120°-30°=90°,
∴是直角三角形;
(2)的形状可以是等腰三角形,理由如下:
①当QA=QP时,∠QAP=∠QPA=30°,
∴=∠QAP+∠QPA=60°,
②当PA=PQ时,∠PQA=,
∴=180°-75°=105°,
③当AQ=AP时,∠AQP=∠APQ=30°,
∴∠QAP=120°=∠BAC,即点P与点C重合,不符合题意,
综上所述,的度数为60°或105°.
【点睛】本题主要考查直角三角形的判定定理,等腰三角形的性质定理,熟练掌握等腰三角形的性质定理以及分类讨论思想,是解题的关键.
24.(1)见解析;(2),,,
【分析】(1)根据平行线的性质和判定可以解答;
(2)由已知及(1)的结论可知∠CFN=45°,然后结合图形根据角度的加减运算可以得到解答.
【详解】(1)证明:∵,∴.
∵平分,平分,∴,.
∴.
∴.
(2)由(1)知ABCD,
∴∠AEF+∠CFE=180°,
∵∠AEF=2∠CFN=∠CFE,
∴∠AEF=∠CFE=90°,
∴∠CFN=∠EFN=∠FEM=∠BEM=45°,∠BEG=∠CFH=∠DFE=90°,
∴∠AEM=∠GEM=∠HFN=∠DFN=90°+45°=135°,
∴度数为135°的角有:、 、 、 .
【点睛】本题考查平行线的判定和性质及角平分线的综合运用,熟练掌握平行线的判定和性质定理及角平分线的意义是解题关键.
25.(1)25;(2)①∠FNC=90°﹣α;②45°.
【分析】(1)根据平行线的性质和互余解答即可;
(2)①过F作FP//AB,根据平行线的性质解答即可;
②过F作FQ//AB,根据平行线的性质解答即可.
【详解】(1)∵∠EFG=90°,∠EFB=65°,
∴∠BFD=90°﹣65°=25°,
∵AB//CD,
∴∠FNC=∠BFD=25°,
故答案为:25;
(2)①如图,过F作FP//AB,连接EG,
∵AB//CD,
∴AB//CD//FP,
∴∠MFP=∠EMB=α,
又∵∠EFG=90°,
∴∠PFN=90°﹣α,
∵FP//CD,
∴∠FNC=∠PFN=90°﹣α;
②如图,过F作FQ//AB,
∵AB//CD,
∴AB//CD//FQ,
∴∠MFQ=∠AMF,∠QFN=∠CNF,
∴∠AMF+∠CNF=∠MFQ+∠QFN=∠EFG=90°,
过H作HR//AB,
∵AB//CD,
∴AB//CD//HR,
∴∠AMH=∠MHR,∠HNC=∠NHR,
又∵MH平分∠AMF,NH平分∠CNF,
∴∠AMH=∠AMF,∠HNC=∠CNF,
∴∠MHN=∠MHR+∠NHR=∠AMH+∠HNC=(∠AMF+∠CNF)=×90°=45°.
【点睛】本题考查平行线的性质、角平分线的性质、角的和差等知识,是重要考点,难度较易,掌握相关知识是解题关键.
