苏科版七年级数学下学期期末专项复习 专题01平面图形的认识(含解析)
文档属性
| 名称 | 苏科版七年级数学下学期期末专项复习 专题01平面图形的认识(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 12:34:25 | ||
图片预览



文档简介
专题01 平面图形的认识-七年级数学下学期期末专项复习(苏科版)
专题01 平面图形的认识
(时间100分,总分120分)
一、选择题:(每题3分,共24分)
1.如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图所示,在下列四组条件中,能判断的是( )
A. B.
C. D.
3.如图,已知直线,被直线所截,且,若,则的度数为( )
A. B. C. D.
4.如图,已知,平分,,则为( )
A. B. C. D.
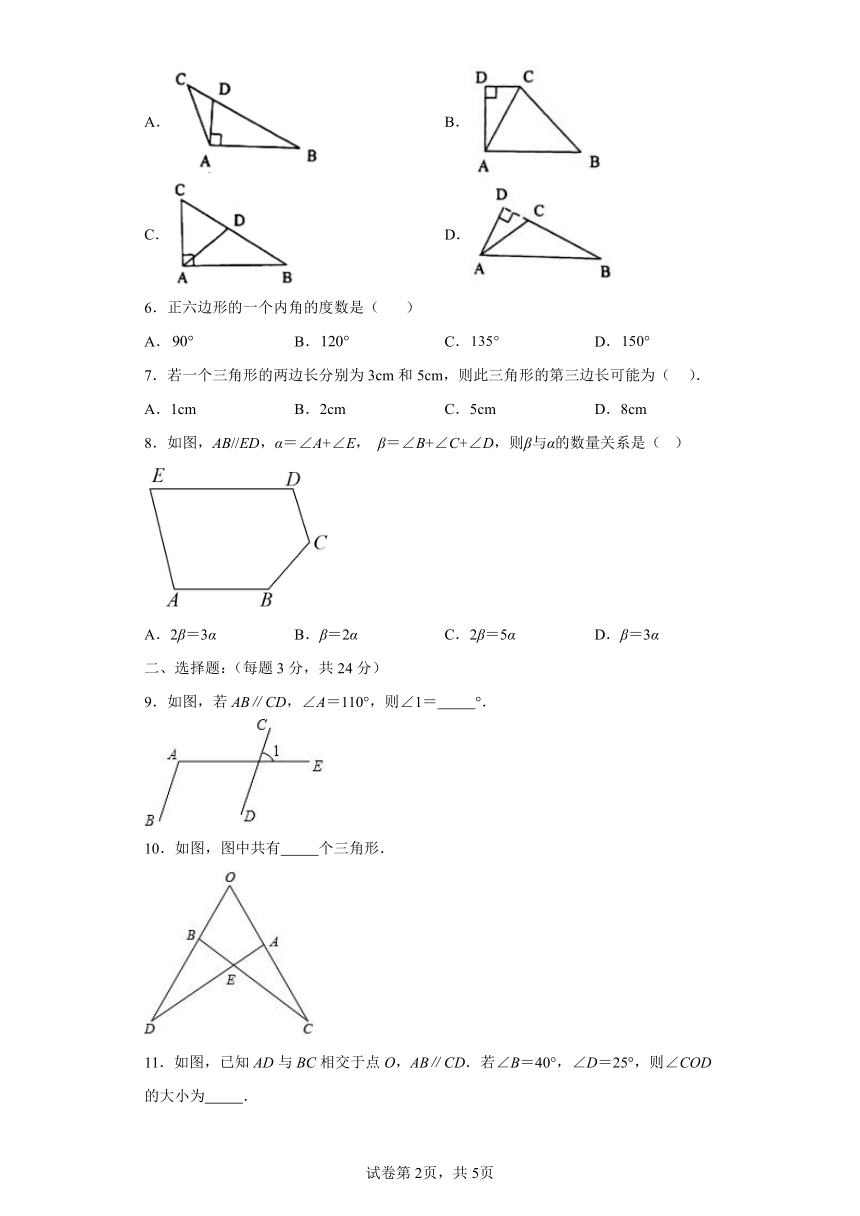
5.下面四个图形中,线段是的高的是( )
A. B.
C. D.
6.正六边形的一个内角的度数是( )
A. B. C. D.
7.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( ).
A.1cm B.2cm C.5cm D.8cm
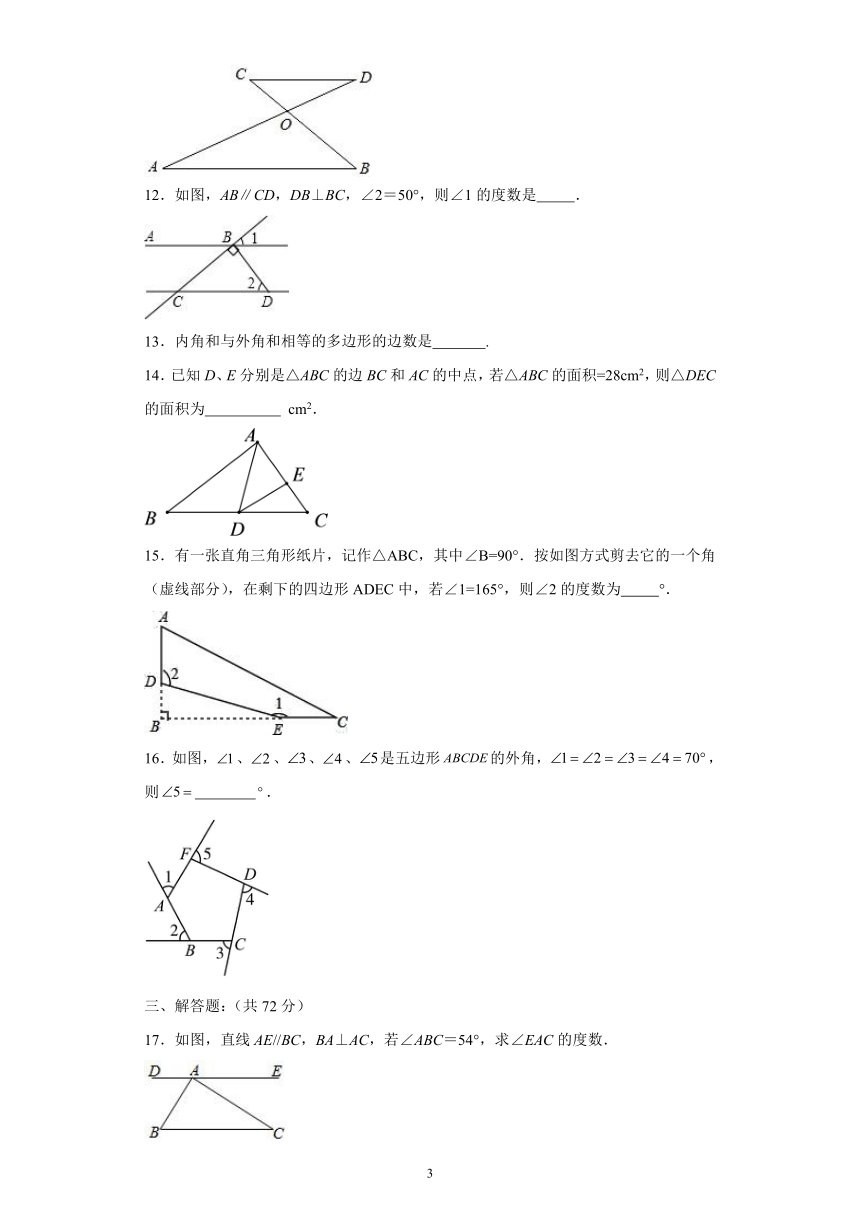
8.如图,AB//ED,α=∠A+∠E, β=∠B+∠C+∠D,则β与α的数量关系是( )
A.2β=3α B.β=2α C.2β=5α D.β=3α
二、选择题:(每题3分,共24分)
9.如图,若AB∥CD,∠A=110°,则∠1= °.
10.如图,图中共有 个三角形.
11.如图,已知AD与BC相交于点O,AB∥CD.若∠B=40°,∠D=25°,则∠COD的大小为 .
12.如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是 .
13.内角和与外角和相等的多边形的边数是 .
14.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=28cm2,则△DEC的面积为 cm2.
15.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 °.
16.如图,、、、、是五边形的外角,,则 .
三、解答题:(共72分)
17.如图,直线AE//BC,BA⊥AC,若∠ABC=54°,求∠EAC的度数.
18.如图,BE∥CG,∠1=∠2,求证:BD∥CF
19.如图,在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数.
20.在 △ABC中,∠BAC=50°,∠B=45°,AD是△ABC的一条角平分线,求∠ADB的度数
21.已知一个n边形,它的内角和等于,求这个n边形的边数.
22.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
23.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
24.如图,平分,与相交于F,,求证:.
参考答案:
1.C
【详解】分析:根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角解答即可.
详解:由同位角的定义可知,∠1的同位角是∠4.
故选C.
点睛:本题考查了同位角问题,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解.
2.D
【分析】根据平行线的判定定理求解判断即可.
【详解】解:A、∵∠1=∠2,
∴ADBC(内错角相等,两直线平行),故此选项不符合题意;
B、∵∠BAD+∠ABC=180°,
∴ADBC(同旁内角互补,两直线平行),故此选项不符合题意;
C、∵∠3=∠4,
∴ADBC(内错角相等,两直线平行),故此选项不符合题意;
D、∵∠ABD=∠BDC,
∴ABCD(内错角相等,两直线平行),故此选项符合题意;
故选:D.
【点睛】此题主要考查了平行线的判定,熟记平行线的判定定理是解题关键.
3.D
【分析】首先根据对顶角相等可得∠1的度数,再根据平行线的性质可得的度数.
【详解】解:∵=40°,
∴∠1==40°,
∵a∥b,
∴=∠1=40°,
故选:D.
【点睛】此题主要考查了对顶角相等和平行线的性质,关键是掌握两直线平行,同位角相等.
4.B
【分析】根据平角的性质可得出∠ABC的度数,再根据平行线的性质两直线平行内错角相等,可得出∠BCD等于∠ABC,由CE平分∠ACD,可得出∠ACD的度数,再由平行线的性质两直线平行同旁内角互补,即可得出答案.
【详解】解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°-∠ACD=180°-60°=120°.
故选:B.
【点睛】主要考查了平行线的性质及角平分线,合理利用平行线的性质进行计算是解决本题的关键.
5.D
【分析】根据三角形高的定义进行判断.
【详解】解:线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
【点睛】本题考查了三角形的高:三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.
6.B
【分析】多边形的内角和可以表示成(6-2) 180°,因为所给多边形的每个内角均相等,可设这个正六边形的每一个内角的度数为x,故又可表示成6x,列方程可求解.
【详解】解:设这个正六边形的每一个内角的度数为x,
则6x=(6-2) 180°,
解得x=120°.
故这个正六边形的每一个内角的度数为120°.
故选:B.
【点睛】本题考查了根据多边形的内角和计算公式求多边形的内角的度数,解答时要会根据公式进行正确运算、变形和数据处理.
7.C
【分析】根据三角形的三边关系求得第三边的取值范围,再看哪个选项内的数在这个范围内即可.
【详解】解:设第三边长xcm.
根据三角形的三边关系,得2<x<8.
∵5cm在第三边长的取值范围内,所以此三角形的第三边长可能为5cm.
故选:C.
【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
8.B
【分析】作CF//ED,利用平行线的性质求得β与α,再判断β与α的数量关系即可.
【详解】解:如图,作CF//ED,
∵AB//ED,
∴∠A+∠E=180°= α ,
∵ED//CF,
∴∠D+∠DCF=180°,
∵AB//ED,ED//CF,
∴AB//CF,
∴∠B+∠BCF=180°,
∴∠D+∠DCF+∠B+∠BCF=180°+180°
即 ∠B+∠C+∠D =360°= β ,
∴ β=2α .
故选B.
【点睛】本题考查了平行线的性质,熟悉运用平行线的性质是解题的关键.
9.70
【分析】先根据平行线的性质求出∠2=∠A=110°,再由平角的定义求出∠1的度数即可.
【详解】如图,
∵AB∥CD,
∴∠2=∠A=110°.
又∵∠1+∠2=180°,
∴∠1=180°﹣∠2=180°﹣110°=70°.
故答案为:70.
【点睛】本题主要考查了平行线的性质,掌握并熟练运用“两直线平行,同位角相等”是解答此题的关键.
10.4
【分析】分别找出图中的三角形即可.
【详解】解:图中有:△OAD,△OBC,△BDE,△ACE,共4个,
故答案为:4.
【点睛】考查了三角形的识别,解题关键是要细心、仔细的数出三角形的个数.
11.115°
【分析】由平行线的性质得出∠C=∠B=40°,再由三角形的内角和定理即可得出结果.
【详解】解:∵AB∥CD,
∴∠C=∠B=25°,
∴∠COD=180°﹣∠C﹣∠D=180°﹣25°﹣40°=115°.
故答案为:115°.
【点睛】本题考查了平行线的性质、三角形的内角和定理;熟练掌握平行线的性质,三角形的内角和定理是解决问题的关键.
12.40°
【分析】在△BCD中,利用三角形内角和定理可求出∠BCD的度数,由AB∥CD,利用“两直线平行,同位角相等”可求出∠1的度数.
【详解】解:在△BCD中,∠CBD=90°,∠2=50°,
∴∠BCD=180°﹣∠CBD﹣∠2=180°﹣90°﹣50°=40°.
∵AB∥CD,
∴∠1=∠BCD=40°.
故答案为:40°.
【点睛】本题难度较低,主要考查学生对平行线性质知识点的掌握,根据两直线平行,同位角相等,判断出直角三角形中,∠BCD=∠1=40°为解题关键.
13.4
【分析】根据多边形的内角和公式(n-2) 180°与多边形的外角和定理列式进行计算即可得解.
【详解】解:设多边形的边数为n,根据题意得
(n-2) 180°=360°,
解得n=4.
∴内角和与外角和相等的多边形的边数是4.
故答案为:4
【点睛】本题考查多边形内角和与外角和,熟记公式正确计算是本题的解题关键,难度不大.
14.7
【分析】根据三角形的面积公式以及中点的概念即可分析出各部分的面积关系.
【详解】解:作高线AM.
∵S△ABC=BC AM,S△ADC=CD AM
又∵D是△ABC的边BC的中点,S△ABC=28cm2,
∴S△ACD=S△ABC=14cm2.
同理,S△CDE=S△ACD=7cm2,
故答案为:7.
【点睛】本题主要考查了三角形的中线,三角形的面积公式,掌握三角形在高相等的时候,面积比等于底的比;在底相等的时候,面积比等于高的比是解题的关键.
15.105° .
【分析】根据三角形内角和定理结合∠B的度数即可得出∠BDE+∠BED的度数,再根据∠BDE与∠2互补、∠BED与∠1互补,即可求出∠1+∠2的度数,代入∠1=165°即可得出结论.
【详解】∵∠B=90°,
∴∠BDE+∠BED=180°-∠B=90°,
又∵∠BDE+∠2=180°,∠BED+∠1=180°,
∴∠1+∠2=360°-(∠BDE+∠BED)=270°.
∵∠1=165°,
∴∠2=105°.
故答案为:105.
【点睛】本题考查了三角形内角和定理,根据三角形内角和定理求出∠BDE+∠BED的度数是解题的关键.
16.80
【分析】根据多边形的外角和为360°,直接算出即可.
【详解】解:∵多边形的外角和为360°,,
∴∠5=360°-70°-70°-70°-70°=80°,
故答案为:80.
【点睛】本题是对多边形外角和的考查,熟练掌握多边形外角和的知识是解决本题的关键.
17.36°.
【分析】根据平行线的性质和直角三角形的性质求解即可.
【详解】∵BA⊥AC,
∴∠BAC=90°,
∵∠ABC=54°,
∴∠C=90°-54°=36°,
∵AE//BC,
∴∠EAC=∠C=36°.
【点睛】本题考查了平行线的性质,直角三角形两锐角互余,熟悉平行线的性质,理解直角三角形两锐角互余是解题的关键.
18.详见解析.
【分析】只要证明∠ABD=∠ACF,根据同位角相等两直线平行即可证明.
【详解】证明:∵BE∥CG,
∴∠ABE=∠ACG,
∵∠1=∠2,
∴∠ABD=∠ACF,
∴BD∥CF.
【点睛】本题考查平行线的判定和性质,解题的关键是熟练掌握平行线的性质和判定,属于中考基础题.
19.∠C的度数为40°
【分析】根据直角三角形的两个锐角互余即可求出∠A,然后根据三角形的内角和定理即可求出结论.
【详解】解:在Rt△ABE中,∠AEB=90°,∠B=30°
∴∠A=90°- ∠B=60°
在△ADC中,∠A=60°,∠ADC=80°
∴∠C=180°- 60° - 80°=40°
答:∠C的度数为40°.
【点睛】此题考查的是三角形的内角和定理的应用,掌握三角形的内角和定理和直角三角形的两个锐角互余是解决此题的关键.
20.∠ADB=110°
【分析】先根据角的平分线求出∠BAD的度数,然后在△ABD中,利用三角形的内角和可求出∠ADB的度数.
【详解】解:∵AD是△ABC的一条角平分线,
∴∠BAD=∠BAC=×50°=25°,
∴∠ADB=180°-∠BAD-∠B=180°-25°-45°=110°.
21.十二边形.
【分析】这个多边形的边数为n,根据多边形的内角和定理即可列方程求解.
【详解】解:这个多边形是边形,根据题意得:,
解得:.
故这个多边形是十二边形.
【点睛】解题的关键是读懂题意,根据多边形的内角和:180°(n-2),正确列方程求解.
22.9cm
【分析】根据中线的定义知CD=BD.结合三角形周长公式知AC-AB=5cm;又AC+AB=13cm.易求AC的长度.
【详解】解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长-△ABD的周长=5cm.
∴AC-AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
【点睛】本题考查了三角形的中线,根据周长的差表示出AC-AB=5cm,是解题的关键.
23.x=85°
【分析】根据平行线的性质先求∠B的度数,再根据五边形的内角和公式求x的值.
【详解】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【点睛】本题主要考查了平行线的性质和多边形的内角和知识点,属于基础题.
24.见解析
【分析】由AB∥CD,可知∠1=∠CFE;由AE平分∠BAD,得到∠1=∠2,再由已知可得∠2=∠E,即可证明AD∥BC.
【详解】解:∵AB∥CD,
∴∠1=∠CFE,
∵AE平分∠BAD,
∴∠1=∠2,
∵∠CFE=∠E,
∴∠2=∠E,
∴AD∥BC.
【点睛】本题考查角平分线的性质以及平行线的判定定理.关键是利用平行线的性质以及角平分线的性质解答.
专题01 平面图形的认识
(时间100分,总分120分)
一、选择题:(每题3分,共24分)
1.如图,直线a,b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图所示,在下列四组条件中,能判断的是( )
A. B.
C. D.
3.如图,已知直线,被直线所截,且,若,则的度数为( )
A. B. C. D.
4.如图,已知,平分,,则为( )
A. B. C. D.
5.下面四个图形中,线段是的高的是( )
A. B.
C. D.
6.正六边形的一个内角的度数是( )
A. B. C. D.
7.若一个三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能为( ).
A.1cm B.2cm C.5cm D.8cm
8.如图,AB//ED,α=∠A+∠E, β=∠B+∠C+∠D,则β与α的数量关系是( )
A.2β=3α B.β=2α C.2β=5α D.β=3α
二、选择题:(每题3分,共24分)
9.如图,若AB∥CD,∠A=110°,则∠1= °.
10.如图,图中共有 个三角形.
11.如图,已知AD与BC相交于点O,AB∥CD.若∠B=40°,∠D=25°,则∠COD的大小为 .
12.如图,AB∥CD,DB⊥BC,∠2=50°,则∠1的度数是 .
13.内角和与外角和相等的多边形的边数是 .
14.已知D、E分别是△ABC的边BC和AC的中点,若△ABC的面积=28cm2,则△DEC的面积为 cm2.
15.有一张直角三角形纸片,记作△ABC,其中∠B=90°.按如图方式剪去它的一个角(虚线部分),在剩下的四边形ADEC中,若∠1=165°,则∠2的度数为 °.
16.如图,、、、、是五边形的外角,,则 .
三、解答题:(共72分)
17.如图,直线AE//BC,BA⊥AC,若∠ABC=54°,求∠EAC的度数.
18.如图,BE∥CG,∠1=∠2,求证:BD∥CF
19.如图,在Rt△ABE中,∠AEB=90°,C为AE延长线上的一点,D为AB边上的一点,DC交BE于F,若∠ADC=80°,∠B=30°,求∠C的度数.
20.在 △ABC中,∠BAC=50°,∠B=45°,AD是△ABC的一条角平分线,求∠ADB的度数
21.已知一个n边形,它的内角和等于,求这个n边形的边数.
22.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
23.如图,在五边形ABCDE中满足 AB∥CD,求图形中的x的值.
24.如图,平分,与相交于F,,求证:.
参考答案:
1.C
【详解】分析:根据同位角就是:两个角都在截线的同旁,又分别处在被截的两条直线同侧的位置的角解答即可.
详解:由同位角的定义可知,∠1的同位角是∠4.
故选C.
点睛:本题考查了同位角问题,解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解.
2.D
【分析】根据平行线的判定定理求解判断即可.
【详解】解:A、∵∠1=∠2,
∴ADBC(内错角相等,两直线平行),故此选项不符合题意;
B、∵∠BAD+∠ABC=180°,
∴ADBC(同旁内角互补,两直线平行),故此选项不符合题意;
C、∵∠3=∠4,
∴ADBC(内错角相等,两直线平行),故此选项不符合题意;
D、∵∠ABD=∠BDC,
∴ABCD(内错角相等,两直线平行),故此选项符合题意;
故选:D.
【点睛】此题主要考查了平行线的判定,熟记平行线的判定定理是解题关键.
3.D
【分析】首先根据对顶角相等可得∠1的度数,再根据平行线的性质可得的度数.
【详解】解:∵=40°,
∴∠1==40°,
∵a∥b,
∴=∠1=40°,
故选:D.
【点睛】此题主要考查了对顶角相等和平行线的性质,关键是掌握两直线平行,同位角相等.
4.B
【分析】根据平角的性质可得出∠ABC的度数,再根据平行线的性质两直线平行内错角相等,可得出∠BCD等于∠ABC,由CE平分∠ACD,可得出∠ACD的度数,再由平行线的性质两直线平行同旁内角互补,即可得出答案.
【详解】解:∵∠ABE=150°,
∴∠ABC=30°,
又∵AB∥CD,
∴∠ABC=∠BCD=30°,
∵CE平分∠ACD,
∴∠ACD=2∠BCD=60°,
又∵AB∥CD,
∴∠A+∠ACD=180°,
∴∠A=180°-∠ACD=180°-60°=120°.
故选:B.
【点睛】主要考查了平行线的性质及角平分线,合理利用平行线的性质进行计算是解决本题的关键.
5.D
【分析】根据三角形高的定义进行判断.
【详解】解:线段AD是△ABC的高,则过点A作对边BC的垂线,则垂线段AD为△ABC的高.
选项A、B、C错误,
故选:D.
【点睛】本题考查了三角形的高:三角形的高是指从三角形的一个顶点向对边作垂线,连接顶点与垂足之间的线段.
6.B
【分析】多边形的内角和可以表示成(6-2) 180°,因为所给多边形的每个内角均相等,可设这个正六边形的每一个内角的度数为x,故又可表示成6x,列方程可求解.
【详解】解:设这个正六边形的每一个内角的度数为x,
则6x=(6-2) 180°,
解得x=120°.
故这个正六边形的每一个内角的度数为120°.
故选:B.
【点睛】本题考查了根据多边形的内角和计算公式求多边形的内角的度数,解答时要会根据公式进行正确运算、变形和数据处理.
7.C
【分析】根据三角形的三边关系求得第三边的取值范围,再看哪个选项内的数在这个范围内即可.
【详解】解:设第三边长xcm.
根据三角形的三边关系,得2<x<8.
∵5cm在第三边长的取值范围内,所以此三角形的第三边长可能为5cm.
故选:C.
【点睛】此题主要考查了三角形的三边关系,要注意三角形形成的条件:任意两边之和大于第三边,任意两边之差小于第三边.
8.B
【分析】作CF//ED,利用平行线的性质求得β与α,再判断β与α的数量关系即可.
【详解】解:如图,作CF//ED,
∵AB//ED,
∴∠A+∠E=180°= α ,
∵ED//CF,
∴∠D+∠DCF=180°,
∵AB//ED,ED//CF,
∴AB//CF,
∴∠B+∠BCF=180°,
∴∠D+∠DCF+∠B+∠BCF=180°+180°
即 ∠B+∠C+∠D =360°= β ,
∴ β=2α .
故选B.
【点睛】本题考查了平行线的性质,熟悉运用平行线的性质是解题的关键.
9.70
【分析】先根据平行线的性质求出∠2=∠A=110°,再由平角的定义求出∠1的度数即可.
【详解】如图,
∵AB∥CD,
∴∠2=∠A=110°.
又∵∠1+∠2=180°,
∴∠1=180°﹣∠2=180°﹣110°=70°.
故答案为:70.
【点睛】本题主要考查了平行线的性质,掌握并熟练运用“两直线平行,同位角相等”是解答此题的关键.
10.4
【分析】分别找出图中的三角形即可.
【详解】解:图中有:△OAD,△OBC,△BDE,△ACE,共4个,
故答案为:4.
【点睛】考查了三角形的识别,解题关键是要细心、仔细的数出三角形的个数.
11.115°
【分析】由平行线的性质得出∠C=∠B=40°,再由三角形的内角和定理即可得出结果.
【详解】解:∵AB∥CD,
∴∠C=∠B=25°,
∴∠COD=180°﹣∠C﹣∠D=180°﹣25°﹣40°=115°.
故答案为:115°.
【点睛】本题考查了平行线的性质、三角形的内角和定理;熟练掌握平行线的性质,三角形的内角和定理是解决问题的关键.
12.40°
【分析】在△BCD中,利用三角形内角和定理可求出∠BCD的度数,由AB∥CD,利用“两直线平行,同位角相等”可求出∠1的度数.
【详解】解:在△BCD中,∠CBD=90°,∠2=50°,
∴∠BCD=180°﹣∠CBD﹣∠2=180°﹣90°﹣50°=40°.
∵AB∥CD,
∴∠1=∠BCD=40°.
故答案为:40°.
【点睛】本题难度较低,主要考查学生对平行线性质知识点的掌握,根据两直线平行,同位角相等,判断出直角三角形中,∠BCD=∠1=40°为解题关键.
13.4
【分析】根据多边形的内角和公式(n-2) 180°与多边形的外角和定理列式进行计算即可得解.
【详解】解:设多边形的边数为n,根据题意得
(n-2) 180°=360°,
解得n=4.
∴内角和与外角和相等的多边形的边数是4.
故答案为:4
【点睛】本题考查多边形内角和与外角和,熟记公式正确计算是本题的解题关键,难度不大.
14.7
【分析】根据三角形的面积公式以及中点的概念即可分析出各部分的面积关系.
【详解】解:作高线AM.
∵S△ABC=BC AM,S△ADC=CD AM
又∵D是△ABC的边BC的中点,S△ABC=28cm2,
∴S△ACD=S△ABC=14cm2.
同理,S△CDE=S△ACD=7cm2,
故答案为:7.
【点睛】本题主要考查了三角形的中线,三角形的面积公式,掌握三角形在高相等的时候,面积比等于底的比;在底相等的时候,面积比等于高的比是解题的关键.
15.105° .
【分析】根据三角形内角和定理结合∠B的度数即可得出∠BDE+∠BED的度数,再根据∠BDE与∠2互补、∠BED与∠1互补,即可求出∠1+∠2的度数,代入∠1=165°即可得出结论.
【详解】∵∠B=90°,
∴∠BDE+∠BED=180°-∠B=90°,
又∵∠BDE+∠2=180°,∠BED+∠1=180°,
∴∠1+∠2=360°-(∠BDE+∠BED)=270°.
∵∠1=165°,
∴∠2=105°.
故答案为:105.
【点睛】本题考查了三角形内角和定理,根据三角形内角和定理求出∠BDE+∠BED的度数是解题的关键.
16.80
【分析】根据多边形的外角和为360°,直接算出即可.
【详解】解:∵多边形的外角和为360°,,
∴∠5=360°-70°-70°-70°-70°=80°,
故答案为:80.
【点睛】本题是对多边形外角和的考查,熟练掌握多边形外角和的知识是解决本题的关键.
17.36°.
【分析】根据平行线的性质和直角三角形的性质求解即可.
【详解】∵BA⊥AC,
∴∠BAC=90°,
∵∠ABC=54°,
∴∠C=90°-54°=36°,
∵AE//BC,
∴∠EAC=∠C=36°.
【点睛】本题考查了平行线的性质,直角三角形两锐角互余,熟悉平行线的性质,理解直角三角形两锐角互余是解题的关键.
18.详见解析.
【分析】只要证明∠ABD=∠ACF,根据同位角相等两直线平行即可证明.
【详解】证明:∵BE∥CG,
∴∠ABE=∠ACG,
∵∠1=∠2,
∴∠ABD=∠ACF,
∴BD∥CF.
【点睛】本题考查平行线的判定和性质,解题的关键是熟练掌握平行线的性质和判定,属于中考基础题.
19.∠C的度数为40°
【分析】根据直角三角形的两个锐角互余即可求出∠A,然后根据三角形的内角和定理即可求出结论.
【详解】解:在Rt△ABE中,∠AEB=90°,∠B=30°
∴∠A=90°- ∠B=60°
在△ADC中,∠A=60°,∠ADC=80°
∴∠C=180°- 60° - 80°=40°
答:∠C的度数为40°.
【点睛】此题考查的是三角形的内角和定理的应用,掌握三角形的内角和定理和直角三角形的两个锐角互余是解决此题的关键.
20.∠ADB=110°
【分析】先根据角的平分线求出∠BAD的度数,然后在△ABD中,利用三角形的内角和可求出∠ADB的度数.
【详解】解:∵AD是△ABC的一条角平分线,
∴∠BAD=∠BAC=×50°=25°,
∴∠ADB=180°-∠BAD-∠B=180°-25°-45°=110°.
21.十二边形.
【分析】这个多边形的边数为n,根据多边形的内角和定理即可列方程求解.
【详解】解:这个多边形是边形,根据题意得:,
解得:.
故这个多边形是十二边形.
【点睛】解题的关键是读懂题意,根据多边形的内角和:180°(n-2),正确列方程求解.
22.9cm
【分析】根据中线的定义知CD=BD.结合三角形周长公式知AC-AB=5cm;又AC+AB=13cm.易求AC的长度.
【详解】解:∵AD是BC边上的中线,
∴D为BC的中点,CD=BD.
∵△ADC的周长-△ABD的周长=5cm.
∴AC-AB=5cm.
又∵AB+AC=13cm,
∴AC=9cm.
【点睛】本题考查了三角形的中线,根据周长的差表示出AC-AB=5cm,是解题的关键.
23.x=85°
【分析】根据平行线的性质先求∠B的度数,再根据五边形的内角和公式求x的值.
【详解】解:∵AB∥CD,∠C=60°,
∴∠B=180°﹣60°=120°,
∴(5﹣2)×180°=x+150°+125°+60°+120°,
∴x=85°.
【点睛】本题主要考查了平行线的性质和多边形的内角和知识点,属于基础题.
24.见解析
【分析】由AB∥CD,可知∠1=∠CFE;由AE平分∠BAD,得到∠1=∠2,再由已知可得∠2=∠E,即可证明AD∥BC.
【详解】解:∵AB∥CD,
∴∠1=∠CFE,
∵AE平分∠BAD,
∴∠1=∠2,
∵∠CFE=∠E,
∴∠2=∠E,
∴AD∥BC.
【点睛】本题考查角平分线的性质以及平行线的判定定理.关键是利用平行线的性质以及角平分线的性质解答.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
