第11章 平面直角坐标系 小结与复习课件(共18张PPT)数学沪科版八年级上册
文档属性
| 名称 | 第11章 平面直角坐标系 小结与复习课件(共18张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 14:49:19 | ||
图片预览






文档简介
(共18张PPT)
小结与复习
第11章 平面直角坐标系
1.平面直角坐标系:
①两条数轴;
②互相垂直;
③原点重合.(如图)
规定:横坐标在前,纵坐标在后
2.研究对象:
点的坐标 — — 有序实数对(x,y)
-3 -2 -1 1 2 3
x
O
-3
-2
-1
1
3
2
y
一、平面直角坐标系与点的坐标:
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
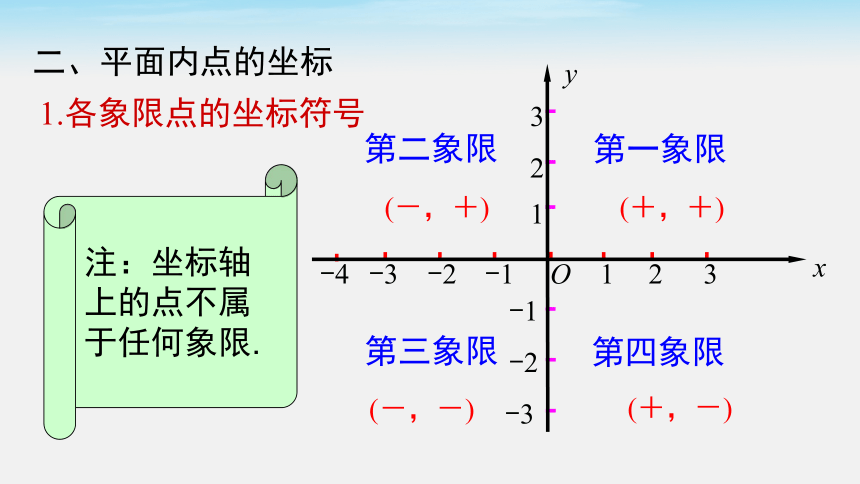
(+,+)
(-,+)
(-,-)
(+,-)
第一象限
第三象限
第二象限
注:坐标轴上的点不属于任何象限.
1.各象限点的坐标符号
二、平面内点的坐标
2.坐标轴上的点 P(x,y)的坐标特征:
(1)x 轴上:x 为任意实数,y 为 0;
(2)y 轴上:x 为 0,y 为任意实数;
(3)坐标原点:x 为 0,y 也为 0.
3.建立直角坐标系的方法很多,在不同的直角坐标系中,同一图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系.
(1)原图形向左(右)平移 a 个单位长度:(a > 0)
向右平移 a 个单位
(2)原图形向上(下)平移 b 个单位长度:(b > 0)
原图形上的点 P(x,y)
向左平移 a 个单位
原图形上的点 P(x,y)
P1(x + a,y)
P2(x - a,y)
向上平移 b 个单位
原图形上的点 P(x,y)
向下平移 b 个单位
原图形上的点 P(x,y)
P3(x,y + b)
P4(x,y - b)
三、图形在坐标系中的平移
考点一 平面直角坐标系与点的坐标
例1 点 P 位于 y 轴左方,距 y 轴 3 个单位长,位于 x 轴上方,距 x 轴 4 个单位长,点 P 的坐标是 ( )
A.(3,﹣4) B.(﹣3,4) C.(4,﹣3) D.(﹣4,3)
【分析】根据平面直角坐标系中点的坐标的几何意义解答.
∵点 P 位于 y 轴左方,∴点的横坐标小于 0.
∵点 P 距 y 轴 3 个单位长,∴点 P 的横坐标是﹣3;
又∵P 点位于 x 轴上方,距 x 轴 4 个单位长,∴点 P 的纵坐标是 4.
B
方法总结
平面直角坐标系中四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).坐标平面上的点到 x 轴的距离等于其纵坐标的绝对值,到 y 中的距离等于其横坐标的绝对值.判断点的位置关键是专注象限内点的坐标的符号特征.
2.若点 P(x,y)的坐标满足 xy>0,则点 P 在第 象限;
1.点 P 的坐标是 (2,-3),则点 P 在第 象限.
四
一或三
3. 若点 P(x,y) 的坐标满足 xy<0,且在 x 轴上方,则点 P 在第 象限.
二
4.若点 A 的坐标为(a2 + 1,-2-b2),则点 A 在第____象限.
四
针对训练
考点二 坐标与平移
例2 在平面直角坐标系中,线段 A′B′ 是由线段 AB 经过平移得到的,已知点 A(﹣2,1)的对应点为 A′(3,1),点 B 的对应点为 B′(4,0),求点 B 的坐标.
【分析】根据对应点 A、A′ 找出平移规律,然后设点 B 的坐标
(x,y),根据平移规律列式求解即可.
解:∵点 A(﹣2,1)的对应点为 A′(3,1),∴3﹣(﹣2) = 3 + 2 = 5,
∴平移规律是横坐标向右平移 5 个单位,纵坐标不变.
设点 B 的坐标为(x,y),则 x + 5 = 4,y = 0,
解得 x =﹣1,y = 0,∴点 B 的坐标为(﹣1,0).
方法总结
5.在平面直角坐标系中,将点 A(x,y)向左平移 5 个单位长度,再向上平移 3 个单位长度后与点B(﹣3,2)重合,则点 A 的坐标是( )
A.(2,5) B.(﹣8,5) C.(﹣8,﹣1) D.(2,﹣1)
在平面直角坐标系中,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.在平面直角坐标系中,一条线段或一个图形怎么移动,那么这个图形上各个点就怎么移动.
D
针对训练
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
O
6.填空
①将△ABC 向左平移 3 个单位后,点 A、B、C 的坐标分别变为______,______,____.
②将△ABC 向下平移 3 个单位后,点A、B、C的坐标分别变为______,________,____.
③若 BC 的坐标不变, △ABC的面积为12,点 A 的横坐标为 -1,那么点 A 的坐标为________________.
(-2,4)
(-7,0)
(-1,0)
(-4,-3)
(1,1)
(2,-3)
(-1,4)或(-1,-4)
考点三 平移作图
例3 如图,直角坐标系中,△ABC 的顶点都在网格点上,其中,C 点坐标为(1,2).
(1)写出点 A、B 的坐标:A( , )、B( , );
(2)将△ABC 先向左平移 2 个单位长度,再向上平移 1个单位长度,得到△A′B′C′,请画出相应
图形,则△A′B′C′ 的三个顶点 坐标分别是
A′( , )、B′( , )、C′( , );
(3)求△ABC 的面积.
2
-1
4
3
0
0
2
4
-1
3
解:(2)平移后图形如图所示;
(3)△ABC 的面积 S = 3×4﹣2× ×1×3﹣ ×2×4 = 5.
A′
B′
C′
方法总结
直角坐标系中的图形左右移动改变点的横坐标,即左减右加;上下平移改变点的纵坐标,即上加下减.求格点中图形的面积通常用割补法,常用长方形的面积减去若干直角三角形的面积表示,或是转化为用几个比较容易求的三角形或四边形的面积和来表示.
7. 如图,把 △ABC 经过一定的变换得到 △A′B′C′,如果△ABC 边上一点 P 的坐标为(a,b),那么 点 P 变换后的对应点 P′ 的
坐标为 .
(a + 3,b + 2)
A(-3,-2)
A′(0,0)
横坐标加 3
纵坐标加 2
针对训练
平面直角坐标系的建立
有序实数对与平面直角坐标系内点的关系
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示点的位置
图形在坐标系内的平移:左减右加,上加下减
坐标平面内的点与有序数对是一一对应的.
掌握 x 轴,y 轴上点的坐标的特点:
x 轴上的点的纵坐标为 0,表示为 (x,0)
y 轴上的点的横坐标为 0,表示为 (0,y)
第一象限:( + ,+ )
第二象限:(- ,+ )
第三象限:(- ,-)
第四象限:( + ,-)
见章末练习
小结与复习
第11章 平面直角坐标系
1.平面直角坐标系:
①两条数轴;
②互相垂直;
③原点重合.(如图)
规定:横坐标在前,纵坐标在后
2.研究对象:
点的坐标 — — 有序实数对(x,y)
-3 -2 -1 1 2 3
x
O
-3
-2
-1
1
3
2
y
一、平面直角坐标系与点的坐标:
第四象限
1
2
3
-1
-2
-3
y
x
1
2
3
-1
-2
-3
-4
O
(+,+)
(-,+)
(-,-)
(+,-)
第一象限
第三象限
第二象限
注:坐标轴上的点不属于任何象限.
1.各象限点的坐标符号
二、平面内点的坐标
2.坐标轴上的点 P(x,y)的坐标特征:
(1)x 轴上:x 为任意实数,y 为 0;
(2)y 轴上:x 为 0,y 为任意实数;
(3)坐标原点:x 为 0,y 也为 0.
3.建立直角坐标系的方法很多,在不同的直角坐标系中,同一图形的顶点坐标也不同,应根据具体情况建立适当的直角坐标系.
(1)原图形向左(右)平移 a 个单位长度:(a > 0)
向右平移 a 个单位
(2)原图形向上(下)平移 b 个单位长度:(b > 0)
原图形上的点 P(x,y)
向左平移 a 个单位
原图形上的点 P(x,y)
P1(x + a,y)
P2(x - a,y)
向上平移 b 个单位
原图形上的点 P(x,y)
向下平移 b 个单位
原图形上的点 P(x,y)
P3(x,y + b)
P4(x,y - b)
三、图形在坐标系中的平移
考点一 平面直角坐标系与点的坐标
例1 点 P 位于 y 轴左方,距 y 轴 3 个单位长,位于 x 轴上方,距 x 轴 4 个单位长,点 P 的坐标是 ( )
A.(3,﹣4) B.(﹣3,4) C.(4,﹣3) D.(﹣4,3)
【分析】根据平面直角坐标系中点的坐标的几何意义解答.
∵点 P 位于 y 轴左方,∴点的横坐标小于 0.
∵点 P 距 y 轴 3 个单位长,∴点 P 的横坐标是﹣3;
又∵P 点位于 x 轴上方,距 x 轴 4 个单位长,∴点 P 的纵坐标是 4.
B
方法总结
平面直角坐标系中四个象限的符号特点分别是:第一象限(+,+);第二象限(﹣,+);第三象限(﹣,﹣);第四象限(+,﹣).坐标平面上的点到 x 轴的距离等于其纵坐标的绝对值,到 y 中的距离等于其横坐标的绝对值.判断点的位置关键是专注象限内点的坐标的符号特征.
2.若点 P(x,y)的坐标满足 xy>0,则点 P 在第 象限;
1.点 P 的坐标是 (2,-3),则点 P 在第 象限.
四
一或三
3. 若点 P(x,y) 的坐标满足 xy<0,且在 x 轴上方,则点 P 在第 象限.
二
4.若点 A 的坐标为(a2 + 1,-2-b2),则点 A 在第____象限.
四
针对训练
考点二 坐标与平移
例2 在平面直角坐标系中,线段 A′B′ 是由线段 AB 经过平移得到的,已知点 A(﹣2,1)的对应点为 A′(3,1),点 B 的对应点为 B′(4,0),求点 B 的坐标.
【分析】根据对应点 A、A′ 找出平移规律,然后设点 B 的坐标
(x,y),根据平移规律列式求解即可.
解:∵点 A(﹣2,1)的对应点为 A′(3,1),∴3﹣(﹣2) = 3 + 2 = 5,
∴平移规律是横坐标向右平移 5 个单位,纵坐标不变.
设点 B 的坐标为(x,y),则 x + 5 = 4,y = 0,
解得 x =﹣1,y = 0,∴点 B 的坐标为(﹣1,0).
方法总结
5.在平面直角坐标系中,将点 A(x,y)向左平移 5 个单位长度,再向上平移 3 个单位长度后与点B(﹣3,2)重合,则点 A 的坐标是( )
A.(2,5) B.(﹣8,5) C.(﹣8,﹣1) D.(2,﹣1)
在平面直角坐标系中,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.在平面直角坐标系中,一条线段或一个图形怎么移动,那么这个图形上各个点就怎么移动.
D
针对训练
y
A
B
C
O
(1,4)
(-4,0)
(2,0)
C
y
A
B
(-4,0)
(2,0)
O
6.填空
①将△ABC 向左平移 3 个单位后,点 A、B、C 的坐标分别变为______,______,____.
②将△ABC 向下平移 3 个单位后,点A、B、C的坐标分别变为______,________,____.
③若 BC 的坐标不变, △ABC的面积为12,点 A 的横坐标为 -1,那么点 A 的坐标为________________.
(-2,4)
(-7,0)
(-1,0)
(-4,-3)
(1,1)
(2,-3)
(-1,4)或(-1,-4)
考点三 平移作图
例3 如图,直角坐标系中,△ABC 的顶点都在网格点上,其中,C 点坐标为(1,2).
(1)写出点 A、B 的坐标:A( , )、B( , );
(2)将△ABC 先向左平移 2 个单位长度,再向上平移 1个单位长度,得到△A′B′C′,请画出相应
图形,则△A′B′C′ 的三个顶点 坐标分别是
A′( , )、B′( , )、C′( , );
(3)求△ABC 的面积.
2
-1
4
3
0
0
2
4
-1
3
解:(2)平移后图形如图所示;
(3)△ABC 的面积 S = 3×4﹣2× ×1×3﹣ ×2×4 = 5.
A′
B′
C′
方法总结
直角坐标系中的图形左右移动改变点的横坐标,即左减右加;上下平移改变点的纵坐标,即上加下减.求格点中图形的面积通常用割补法,常用长方形的面积减去若干直角三角形的面积表示,或是转化为用几个比较容易求的三角形或四边形的面积和来表示.
7. 如图,把 △ABC 经过一定的变换得到 △A′B′C′,如果△ABC 边上一点 P 的坐标为(a,b),那么 点 P 变换后的对应点 P′ 的
坐标为 .
(a + 3,b + 2)
A(-3,-2)
A′(0,0)
横坐标加 3
纵坐标加 2
针对训练
平面直角坐标系的建立
有序实数对与平面直角坐标系内点的关系
象限与象限内点的符号
特殊位置点的坐标
坐标系的应用
用坐标表示点的位置
图形在坐标系内的平移:左减右加,上加下减
坐标平面内的点与有序数对是一一对应的.
掌握 x 轴,y 轴上点的坐标的特点:
x 轴上的点的纵坐标为 0,表示为 (x,0)
y 轴上的点的横坐标为 0,表示为 (0,y)
第一象限:( + ,+ )
第二象限:(- ,+ )
第三象限:(- ,-)
第四象限:( + ,-)
见章末练习
