2.4绝对值 课件(共17张PPT) 2023—2024学年华东师大版数学七年级上册
文档属性
| 名称 | 2.4绝对值 课件(共17张PPT) 2023—2024学年华东师大版数学七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 388.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 15:30:19 | ||
图片预览




文档简介
(共17张PPT)
第2章 有理数
2.4 绝对值
在一些量的计算中,有时并不注重其方向.例如,计算汽车行驶所耗的汽油,需要关注的是汽车行驶的路程,而无需关注其行驶的方向.
在讨论数轴上的点与原点的距离时,只需要观察它与原点之间相隔多少个单位长度,而与它位于原点哪一边无关.
新课引入
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
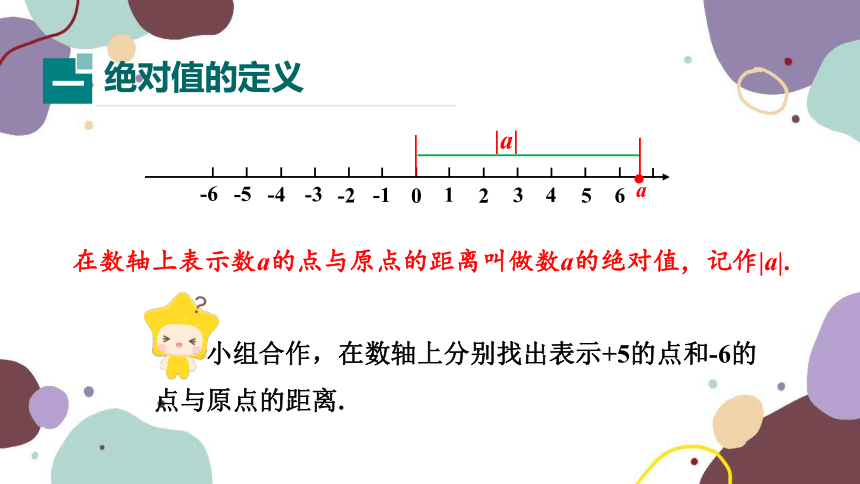
在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
a
小组合作,在数轴上分别找出表示+5的点和-6的点与原点的距离.
|a|
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
6
在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
小组合作,在数轴上分别找出表示+5的点和-6的点与原点的距离.
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
6
通过在数轴上找点,可得:表示-5的点与原点的距离是5,所以+5的绝对值是5,记作|+5|=5;
在数轴上表示-6的点与原点的距离是6,所以-6的绝对值是6,记作|-6|=6.
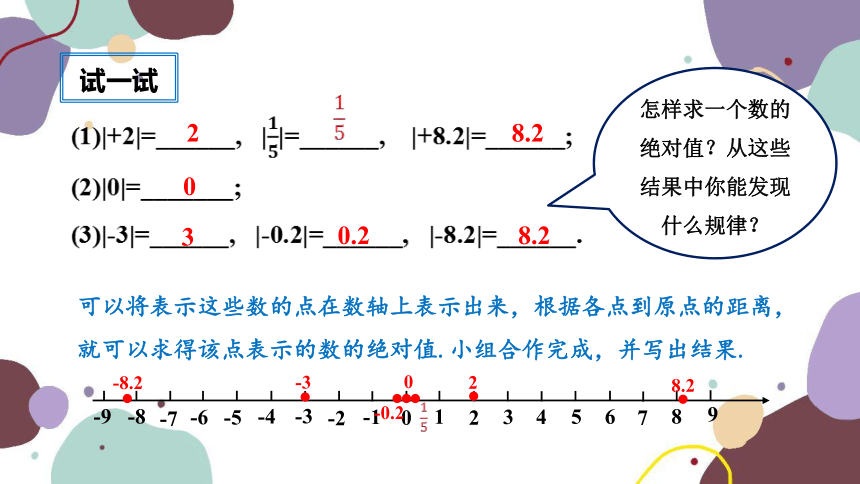
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
可以将表示这些数的点在数轴上表示出来,根据各点到原点的距离,就可以求得该点表示的数的绝对值.小组合作完成,并写出结果.
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
7
8
9
-7
-8
-9
2
8.2
0
3
0.2
8.2
8.2
-8.2
0
-0.2
-3
2
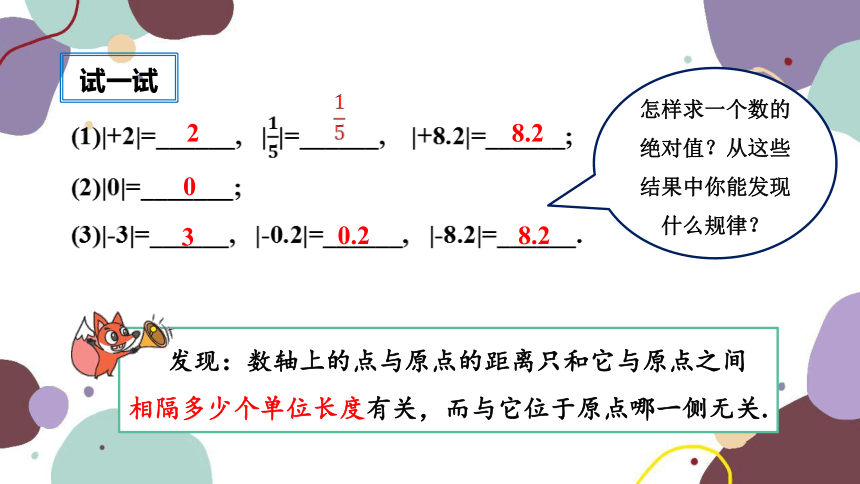
试一试
发现:数轴上的点与原点的距离只和它与原点之间
相隔多少个单位长度有关,而与它位于原点哪一侧无关.
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
2
8.2
0
3
0.2
8.2
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
2
8.2
0
3
0.2
8.2
发现规律:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
绝对值的性质
二
发现规律:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
你能将上面的结论用数学式子表示吗?
当a>0时,|a|=_____;
当a=0时, |a|=_____;
当a<0时,|a|=_____.
a
0
-a
任何一个有理数的绝对值总是正数或0.
即对任意有理数a,总有|a| ≥0.
(1)求任意有理数a的绝对值时,要分类讨论,讨论a为非负数和负数两种情况.
(2)互为相反数的两个数绝对值相等,绝对值相等的两个数可能相等,也可能互为相反数.
(3)绝对值等于它本身的数有正数和0.
去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的定义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
求一个数的绝对值的方法
化简含绝对值符号的式子时,要先求绝对值,再按照双重符号化简规则进行化简.
1.下列说法正确的是( )
A.|-3|是求-3的相反数
B.|-3|表示的意义是数轴上表示-3的点到原点的距离
C.|-3|的意义是表示-3的点到原点的距离是 -3
D.以上都不对
B
2.如图,点A所表示的有理数的绝对值是( )
A.-1 B.1 C.±1 D.以上都不对
B
随堂练习
3.若|x|=x,则x是( )
A.正数 B.0
C.非负数 D.非正数
解析:|x|=x表示的意义是:一个数的绝对值等于它本身;而绝对值等于它本身的数是正数和0,即非负数.
C
随堂练习
随堂练习
求绝对值时,只关注绝对值符号里边数的运算,绝对值外面的符号不参与绝对值的运算;运算时,先去掉绝对值符号,再进行其他运算.
课堂小结
有两解(0除外),且这两解互为相反数.
与绝对值有关的两种常见题型
其解法的实质是去掉绝对值符号,去绝对值符号必须按照“先判后去”的原则, 即先判断这个数的正、负性;再按照定义去绝对值符号,要确保其结果为非负数且只有一个;
(1)求一个数的绝对值
(2)已知一个数的绝对值求这个数
第2章 有理数
2.4 绝对值
在一些量的计算中,有时并不注重其方向.例如,计算汽车行驶所耗的汽油,需要关注的是汽车行驶的路程,而无需关注其行驶的方向.
在讨论数轴上的点与原点的距离时,只需要观察它与原点之间相隔多少个单位长度,而与它位于原点哪一边无关.
新课引入
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
a
小组合作,在数轴上分别找出表示+5的点和-6的点与原点的距离.
|a|
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
6
在数轴上表示数a的点与原点的距离叫做数a的绝对值,记作|a|.
小组合作,在数轴上分别找出表示+5的点和-6的点与原点的距离.
绝对值的定义
一
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
5
6
通过在数轴上找点,可得:表示-5的点与原点的距离是5,所以+5的绝对值是5,记作|+5|=5;
在数轴上表示-6的点与原点的距离是6,所以-6的绝对值是6,记作|-6|=6.
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
可以将表示这些数的点在数轴上表示出来,根据各点到原点的距离,就可以求得该点表示的数的绝对值.小组合作完成,并写出结果.
0
1
2
3
4
5
6
-1
-2
-3
-4
-5
-6
7
8
9
-7
-8
-9
2
8.2
0
3
0.2
8.2
8.2
-8.2
0
-0.2
-3
2
试一试
发现:数轴上的点与原点的距离只和它与原点之间
相隔多少个单位长度有关,而与它位于原点哪一侧无关.
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
2
8.2
0
3
0.2
8.2
试一试
怎样求一个数的绝对值?从这些结果中你能发现什么规律?
2
8.2
0
3
0.2
8.2
发现规律:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
绝对值的性质
二
发现规律:一个正数的绝对值是它本身;
零的绝对值是零;
一个负数的绝对值是它的相反数.
你能将上面的结论用数学式子表示吗?
当a>0时,|a|=_____;
当a=0时, |a|=_____;
当a<0时,|a|=_____.
a
0
-a
任何一个有理数的绝对值总是正数或0.
即对任意有理数a,总有|a| ≥0.
(1)求任意有理数a的绝对值时,要分类讨论,讨论a为非负数和负数两种情况.
(2)互为相反数的两个数绝对值相等,绝对值相等的两个数可能相等,也可能互为相反数.
(3)绝对值等于它本身的数有正数和0.
去掉绝对值符号时,必须按照“先判后去”的原则,先判断这个数是正数、0或负数,再根据绝对值的定义去掉绝对值符号,总之要确保其结果为非负数且只有一个.
求一个数的绝对值的方法
化简含绝对值符号的式子时,要先求绝对值,再按照双重符号化简规则进行化简.
1.下列说法正确的是( )
A.|-3|是求-3的相反数
B.|-3|表示的意义是数轴上表示-3的点到原点的距离
C.|-3|的意义是表示-3的点到原点的距离是 -3
D.以上都不对
B
2.如图,点A所表示的有理数的绝对值是( )
A.-1 B.1 C.±1 D.以上都不对
B
随堂练习
3.若|x|=x,则x是( )
A.正数 B.0
C.非负数 D.非正数
解析:|x|=x表示的意义是:一个数的绝对值等于它本身;而绝对值等于它本身的数是正数和0,即非负数.
C
随堂练习
随堂练习
求绝对值时,只关注绝对值符号里边数的运算,绝对值外面的符号不参与绝对值的运算;运算时,先去掉绝对值符号,再进行其他运算.
课堂小结
有两解(0除外),且这两解互为相反数.
与绝对值有关的两种常见题型
其解法的实质是去掉绝对值符号,去绝对值符号必须按照“先判后去”的原则, 即先判断这个数的正、负性;再按照定义去绝对值符号,要确保其结果为非负数且只有一个;
(1)求一个数的绝对值
(2)已知一个数的绝对值求这个数
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
