12.2 第6课时 一次函数与一元一次方程、一元一次不等式 课件 (共26张PPT)数学沪科版八年级上册
文档属性
| 名称 | 12.2 第6课时 一次函数与一元一次方程、一元一次不等式 课件 (共26张PPT)数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 15:13:46 | ||
图片预览






文档简介
(共26张PPT)
第6课时 一次函数与一元一次方程、一元一次不等式
第12章 一次函数
12.2 一次函数
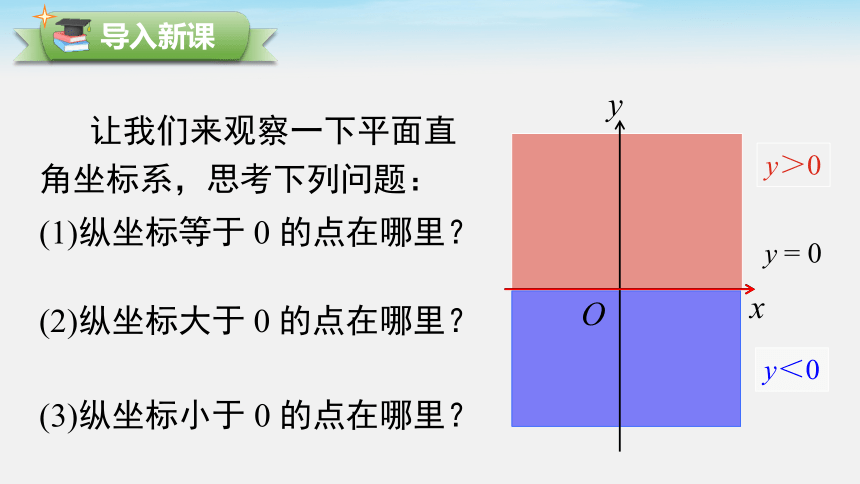
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于 0 的点在哪里?
(2)纵坐标大于 0 的点在哪里?
(3)纵坐标小于 0 的点在哪里?
x
y
O
y = 0
问题1:(1)解方程 2x + 20 = 0;
(2)当自变量 x 为何值时,函数 y = 2x + 20 的值为 0?
解:(1) 2x + 20 = 0
2x = -20
x = -10
(2) 当 y = 0 时 ,即
2x + 20 = 0
2x = -20
x = -10
从“函数值”
角度看
两个问题实际上是同一个问题
一次函数与一元一次方程
(3)画出函数 y = 2x + 20 的图象,并确定它与 x 轴的交点坐标.
O
x
y
20
-10
y = 2x + 20
思考:
直线 y = 2x + 20 与 x 轴交点坐标为(____,___),这说明方程 2x+20=0 的解是 x=_____.
从“函数图象”上看
-10
0
-10
3
2
1
2
1
-2
O
x
y
-1
-1
3
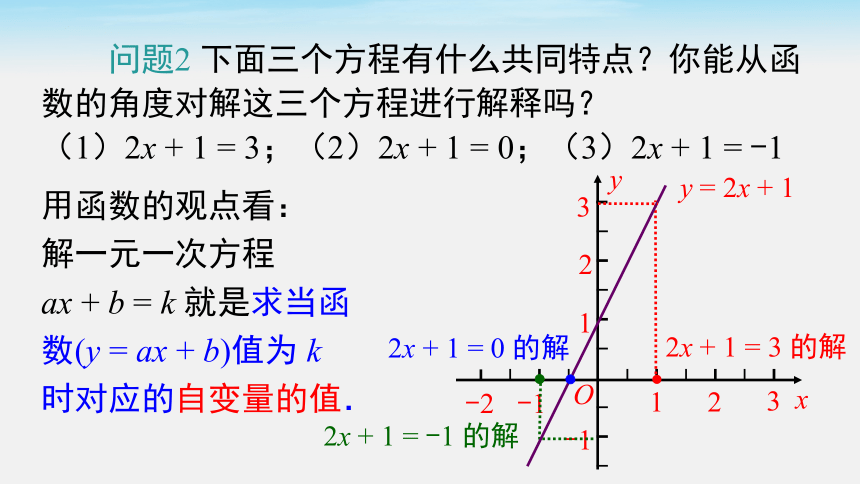
问题2 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x + 1 = 3;(2)2x + 1 = 0;(3)2x + 1 = -1
用函数的观点看:
解一元一次方程
ax + b = k 就是求当函
数(y = ax + b)值为 k
时对应的自变量的值.
2x + 1 = 3 的解
y = 2x + 1
2x + 1 = 0 的解
2x + 1 = -1 的解
1.直线 y = 2x + 20 与 x 轴交点坐标为(____,____),这说明方程 2x+20=0 的解是 x = _____.
-10
0
-10
练一练
2.若方程 kx+2=0 的解是 x = 5,则直线 y = kx+2 与 x 轴交点坐标为(____,_____).
5
0
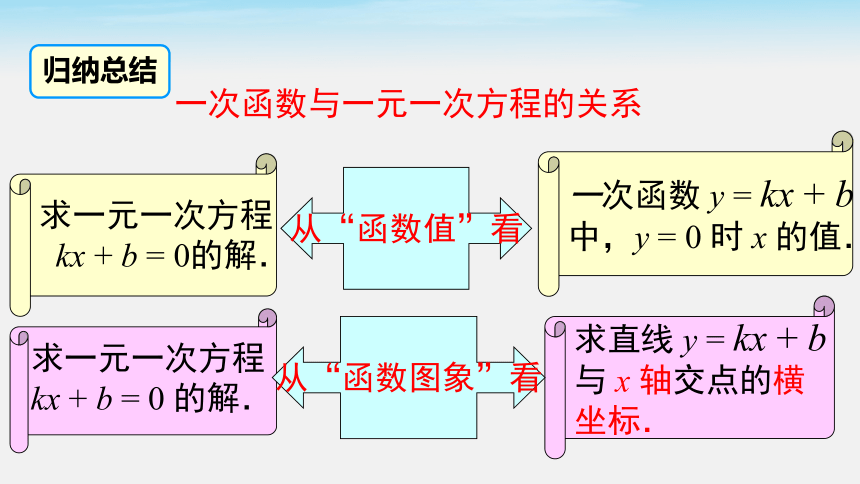
求一元一次方程
kx + b = 0的解.
一次函数与一元一次方程的关系
一次函数 y = kx + b
中,y = 0 时 x 的值.
从“函数值”看
求一元一次方程
kx + b = 0 的解.
求直线 y = kx + b
与 x 轴交点的横
坐标.
从“函数图象”看
归纳总结
例1 直线 y=2x+b 与 x 轴的交点坐标是 (2,0),则关于 x 的方程 2x+b=0 的解是 x=___.
解析:∵直线 y=2x+b 与 x 轴的交点坐标是 (2,0),
则 x=2 时,y=0,
∴关于 x 的方程 2x+b=0 的解是 x=2.
典例精析
2
直线 y=kx+b 与 x 轴交点的横坐标就是方程 kx+b=0 的解,反之亦然.所以在解题时,常需作出一次函数的草图,结合图形分析更加直观、方便.
方法总结
1.已知一次函数 y = 0.8x - 2 与 x 轴的交点为 (2.5,0),你能说出 0.8x - 2 = 0 的解吗?
2.已知一次函数 y = kx - 5 与 x 轴的交点为 (3,0),那么你能说出 kx - 5 = 0 的解吗?
3.已知关于 x 的一元一次方程 mx + n = 0 的解是 -3,则直线 y = mx + n 与 x 轴的交点坐标是_______.
试一试
x = 2.5
x = 3
(-3,0)
例2 一个物体现在的速度是 5 米/秒,其速度每秒增加 2 米/秒,再过几秒它的速度为 17 米/秒?(从方程、函数解析式及图象三个不同方面进行解答)
解法1:设再过 x 秒它的速度为 17 米/秒,
由题意得 2x + 5 = 17
解得 x = 6
答:再过 6 秒它的速度为 17 米/秒.
解法2:速度 y (单位:米/秒)是时间 x (单位:秒)的函数 y = 2x + 5
由 2x + 5 = 17 得 2x-12 = 0
由右图看出直线 y = 2x-12 与 x 轴的交点为 (6,0),得 x = 6.
O
x
y
6
-12
y = 2x-12
由右图可以看出当 y = 17 时,x = 6.
y = 2x + 5
x
y
O
6
17
5
-2.5
解法2:速度 y (单位:米/秒)是时间 x (单位:秒)的函数 y = 2x + 5
观察在 x 轴上方的函数图象所对应的函数值 y 和自变量 x 的取值范围.
y = 2x + 6
思考:它们与不等式 2x + 6>0 及其解集有何关系?
y>0
x>-3
1
2
3
-1
-2
-3
-4
-1
1
2
3
4
5
6
7
O
x
y
A(0,6)
B(0,-3)
一次函数与一元一次不等式
想一想:你能通过观察函数图象得出一次不等式 2x + 6<0 的解集吗?
y = 2x + 6
x<-3
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
2
问题:请同学们观察一次函数 y = 2x + 6 和 y = 3 的图象,你能说出 2x + 6 = 3 的解和 2x + 6>3 的解集吗?
-1.5
1
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
x = -1.5, x>-1.5
y = 2x + 6
y = 3
求 kx + b>0 (或<0)
(k ≠ 0)的解集
一次函数与一元一次不等式的关系
y = kx + b 的值
大于(或小于) 0 时,
x 的取值范围
从“函数值”看
求 kx + b>0 (或<0)
(k ≠ 0)的解集
确定直线 y = kx + b
在 x 轴上方(或下方)
的图象所对应的 x
取值范围
从“函数图象”看
归纳总结
例3 画出函数 y = -3x + 6 的图象,结合图象求:
(1)方程 -3x + 6 = 0 的解;
(2)不等式 -3x + 6>0 和 -3x + 6<0 的解集;
(3)当 x 取何值时,y<3?
解:(1)作出函数 y = -3x + 6 的图象,如图所示,图象与 x 轴交于点 B(2,0).
所以,方程 -3x + 6 = 0 的解就是交点 B 的横坐标.
x
O
B(2,0)
A(0,6)
y
x
O
B(2,0)
A(0,6)
y
(2)不等式 -3x + 6>0 和 -3x + 6<0 的解集;
(3)当 x 取何值时,y<3?
解:(2)由图象可知,不等式 -3x + 6>0 的解集是图象位于 x 轴上方的 x 的取值范围,即 x<2;不等式 -3x + 6<0 的解集是图象位于 x 轴下方的 x 的取值范围,即 x>2;
(3)由图象可知,当 x>1 时,y<3.
3
1
(1,3)
试一试
1.一次函数 y = -x + 2 的图象如图,你能说出 -x + 2<0 的解集吗?
x
y
O
y = -x + 2
2
x>2
2.一次函数 y = kx + b 的图象如图,你能说出 kx + b<0 的解集吗?
x
y
O
y = kx + b
-4
x<-4
1.利用图象解一元一次方程 x + 3 = 0.
3
y = x + 3
O
y
解:作 y = x + 3 图象如右图.
由图象知 y = x + 3 交 x 轴于 (-3,0), 所以原方程的解为 x = 3.
x
3
2.用画函数图象的方法解不等式 5x + 4<2x + 10.
解:原不等式化为 3x - 6<0
画出直线 y = 3x - 6 (如图).
可以看出,当x<2 时这条直线上的点在 x 轴的下方,
即这时 y = 3x - 6<0,所以不等式的解集为 x<2.
y = 3x - 6
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
即 5x + 4<2x + 10 的解集为 x<2.
解:画出两个函数 y = 5x 1
和 y = 2x + 5 的图象.
由图象知,两直线交于点 (2,9),所以原方程的解为 x = 2.
O
y = 5x 1
y = 2x + 5
9
2
x
y
3.利用函数图象求 x 的值.
5x 1 = 2x + 5.
4.函数 y = 2x + 6 的图象如图,利用图象求:
(1)方程 2x + 6 = 0 的解;
由图象可得:图象过点 (-3,0).
∴方程 2x + 6 = 0 的解为 x = -3;
(2)不等式 2x + 6>0 的解集;
由图象可得:当 x>-3 时,函数 y = 2x + 6 的图象在 x 轴上方.
∴不等式 2x + 6>0 的解集为 x>-3;
(3)若 -1≤y≤3,求 x 的取值范围.
由图象可得:函数图象过
F (-1.5,3),G (-3.5,-1) 两点,
当 -3.5≤x≤-1.5 时,函数y = 2x+6的函数值满足-1≤y≤3,
∴x 的取值范围是 -3.5≤x≤-1.5.
一次函数与一元一次方程、一元一次不等式
解一元一次方程可以转化为:当某个一次函数的值为 0 时,求相应的自变量的值,即一次函数与 x 轴交点的横坐标.
解一元一次不等式可以看作:当一次函数的函数值大(小)于 0 时,求自变量相应的取值范围.
第6课时 一次函数与一元一次方程、一元一次不等式
第12章 一次函数
12.2 一次函数
y<0
y>0
让我们来观察一下平面直角坐标系,思考下列问题:
(1)纵坐标等于 0 的点在哪里?
(2)纵坐标大于 0 的点在哪里?
(3)纵坐标小于 0 的点在哪里?
x
y
O
y = 0
问题1:(1)解方程 2x + 20 = 0;
(2)当自变量 x 为何值时,函数 y = 2x + 20 的值为 0?
解:(1) 2x + 20 = 0
2x = -20
x = -10
(2) 当 y = 0 时 ,即
2x + 20 = 0
2x = -20
x = -10
从“函数值”
角度看
两个问题实际上是同一个问题
一次函数与一元一次方程
(3)画出函数 y = 2x + 20 的图象,并确定它与 x 轴的交点坐标.
O
x
y
20
-10
y = 2x + 20
思考:
直线 y = 2x + 20 与 x 轴交点坐标为(____,___),这说明方程 2x+20=0 的解是 x=_____.
从“函数图象”上看
-10
0
-10
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题2 下面三个方程有什么共同特点?你能从函数的角度对解这三个方程进行解释吗?
(1)2x + 1 = 3;(2)2x + 1 = 0;(3)2x + 1 = -1
用函数的观点看:
解一元一次方程
ax + b = k 就是求当函
数(y = ax + b)值为 k
时对应的自变量的值.
2x + 1 = 3 的解
y = 2x + 1
2x + 1 = 0 的解
2x + 1 = -1 的解
1.直线 y = 2x + 20 与 x 轴交点坐标为(____,____),这说明方程 2x+20=0 的解是 x = _____.
-10
0
-10
练一练
2.若方程 kx+2=0 的解是 x = 5,则直线 y = kx+2 与 x 轴交点坐标为(____,_____).
5
0
求一元一次方程
kx + b = 0的解.
一次函数与一元一次方程的关系
一次函数 y = kx + b
中,y = 0 时 x 的值.
从“函数值”看
求一元一次方程
kx + b = 0 的解.
求直线 y = kx + b
与 x 轴交点的横
坐标.
从“函数图象”看
归纳总结
例1 直线 y=2x+b 与 x 轴的交点坐标是 (2,0),则关于 x 的方程 2x+b=0 的解是 x=___.
解析:∵直线 y=2x+b 与 x 轴的交点坐标是 (2,0),
则 x=2 时,y=0,
∴关于 x 的方程 2x+b=0 的解是 x=2.
典例精析
2
直线 y=kx+b 与 x 轴交点的横坐标就是方程 kx+b=0 的解,反之亦然.所以在解题时,常需作出一次函数的草图,结合图形分析更加直观、方便.
方法总结
1.已知一次函数 y = 0.8x - 2 与 x 轴的交点为 (2.5,0),你能说出 0.8x - 2 = 0 的解吗?
2.已知一次函数 y = kx - 5 与 x 轴的交点为 (3,0),那么你能说出 kx - 5 = 0 的解吗?
3.已知关于 x 的一元一次方程 mx + n = 0 的解是 -3,则直线 y = mx + n 与 x 轴的交点坐标是_______.
试一试
x = 2.5
x = 3
(-3,0)
例2 一个物体现在的速度是 5 米/秒,其速度每秒增加 2 米/秒,再过几秒它的速度为 17 米/秒?(从方程、函数解析式及图象三个不同方面进行解答)
解法1:设再过 x 秒它的速度为 17 米/秒,
由题意得 2x + 5 = 17
解得 x = 6
答:再过 6 秒它的速度为 17 米/秒.
解法2:速度 y (单位:米/秒)是时间 x (单位:秒)的函数 y = 2x + 5
由 2x + 5 = 17 得 2x-12 = 0
由右图看出直线 y = 2x-12 与 x 轴的交点为 (6,0),得 x = 6.
O
x
y
6
-12
y = 2x-12
由右图可以看出当 y = 17 时,x = 6.
y = 2x + 5
x
y
O
6
17
5
-2.5
解法2:速度 y (单位:米/秒)是时间 x (单位:秒)的函数 y = 2x + 5
观察在 x 轴上方的函数图象所对应的函数值 y 和自变量 x 的取值范围.
y = 2x + 6
思考:它们与不等式 2x + 6>0 及其解集有何关系?
y>0
x>-3
1
2
3
-1
-2
-3
-4
-1
1
2
3
4
5
6
7
O
x
y
A(0,6)
B(0,-3)
一次函数与一元一次不等式
想一想:你能通过观察函数图象得出一次不等式 2x + 6<0 的解集吗?
y = 2x + 6
x<-3
1
2
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
2
问题:请同学们观察一次函数 y = 2x + 6 和 y = 3 的图象,你能说出 2x + 6 = 3 的解和 2x + 6>3 的解集吗?
-1.5
1
3
-1
-2
-3
-4
1
3
4
5
7
O
A(0,6)
B(0,-3)
2
6
4
-1
x
y
x = -1.5, x>-1.5
y = 2x + 6
y = 3
求 kx + b>0 (或<0)
(k ≠ 0)的解集
一次函数与一元一次不等式的关系
y = kx + b 的值
大于(或小于) 0 时,
x 的取值范围
从“函数值”看
求 kx + b>0 (或<0)
(k ≠ 0)的解集
确定直线 y = kx + b
在 x 轴上方(或下方)
的图象所对应的 x
取值范围
从“函数图象”看
归纳总结
例3 画出函数 y = -3x + 6 的图象,结合图象求:
(1)方程 -3x + 6 = 0 的解;
(2)不等式 -3x + 6>0 和 -3x + 6<0 的解集;
(3)当 x 取何值时,y<3?
解:(1)作出函数 y = -3x + 6 的图象,如图所示,图象与 x 轴交于点 B(2,0).
所以,方程 -3x + 6 = 0 的解就是交点 B 的横坐标.
x
O
B(2,0)
A(0,6)
y
x
O
B(2,0)
A(0,6)
y
(2)不等式 -3x + 6>0 和 -3x + 6<0 的解集;
(3)当 x 取何值时,y<3?
解:(2)由图象可知,不等式 -3x + 6>0 的解集是图象位于 x 轴上方的 x 的取值范围,即 x<2;不等式 -3x + 6<0 的解集是图象位于 x 轴下方的 x 的取值范围,即 x>2;
(3)由图象可知,当 x>1 时,y<3.
3
1
(1,3)
试一试
1.一次函数 y = -x + 2 的图象如图,你能说出 -x + 2<0 的解集吗?
x
y
O
y = -x + 2
2
x>2
2.一次函数 y = kx + b 的图象如图,你能说出 kx + b<0 的解集吗?
x
y
O
y = kx + b
-4
x<-4
1.利用图象解一元一次方程 x + 3 = 0.
3
y = x + 3
O
y
解:作 y = x + 3 图象如右图.
由图象知 y = x + 3 交 x 轴于 (-3,0), 所以原方程的解为 x = 3.
x
3
2.用画函数图象的方法解不等式 5x + 4<2x + 10.
解:原不等式化为 3x - 6<0
画出直线 y = 3x - 6 (如图).
可以看出,当x<2 时这条直线上的点在 x 轴的下方,
即这时 y = 3x - 6<0,所以不等式的解集为 x<2.
y = 3x - 6
1
2
3
-1
-2
-3
-1
-3
-4
-5
2
O
-2
1
4
-6
x
y
即 5x + 4<2x + 10 的解集为 x<2.
解:画出两个函数 y = 5x 1
和 y = 2x + 5 的图象.
由图象知,两直线交于点 (2,9),所以原方程的解为 x = 2.
O
y = 5x 1
y = 2x + 5
9
2
x
y
3.利用函数图象求 x 的值.
5x 1 = 2x + 5.
4.函数 y = 2x + 6 的图象如图,利用图象求:
(1)方程 2x + 6 = 0 的解;
由图象可得:图象过点 (-3,0).
∴方程 2x + 6 = 0 的解为 x = -3;
(2)不等式 2x + 6>0 的解集;
由图象可得:当 x>-3 时,函数 y = 2x + 6 的图象在 x 轴上方.
∴不等式 2x + 6>0 的解集为 x>-3;
(3)若 -1≤y≤3,求 x 的取值范围.
由图象可得:函数图象过
F (-1.5,3),G (-3.5,-1) 两点,
当 -3.5≤x≤-1.5 时,函数y = 2x+6的函数值满足-1≤y≤3,
∴x 的取值范围是 -3.5≤x≤-1.5.
一次函数与一元一次方程、一元一次不等式
解一元一次方程可以转化为:当某个一次函数的值为 0 时,求相应的自变量的值,即一次函数与 x 轴交点的横坐标.
解一元一次不等式可以看作:当一次函数的函数值大(小)于 0 时,求自变量相应的取值范围.
