12.2 第1课时 正比例函数的图象和性质 课件(共33张PPT) 数学沪科版八年级上册
文档属性
| 名称 | 12.2 第1课时 正比例函数的图象和性质 课件(共33张PPT) 数学沪科版八年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 15:25:49 | ||
图片预览










文档简介
(共33张PPT)
第1课时 正比例函数的图象和性质
第12章 一次函数
12.2 一次函数
1.函数有哪些表示方法?
图象法、列表法、解析法
三种方法可以相互转化
它们之间有什么关系?
2.你能将解析法转化成图象法吗?
什么是函数的图象?
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子
一次函数与正比例函数
情景一:某弹簧的自然长度为 3 cm,在弹性限度内,所挂物体的质量 x 每增加 1 kg,弹簧长度 y 增加 0.5 cm.你能写出 y 与 x 之间的关系吗?
y = 3 + 0.5x
情景二:某辆汽车油箱中原有油 100 L,汽车每行驶 50 km 耗油 9 L.设汽车行使路程 x (km),油箱剩余油量 y (L),你能写出 y 与 x 的关系吗?
y =100-0.18x
情景三:每个练习本的厚度为 0.5 cm,一些练习本摞
在一起的总厚度 h(单位:cm)随练习本的本数 n 的
变化而变化.写出函数解析式.
情景四:冷冻一个 0 ℃ 的物体,使它每分钟下降 2 ℃,
物体问题 T(单位:℃)随冷冻时间 t(单位:min)
的变化而变化.写出函数解析式.
h = 0.5n
T = -2t
上面的四个函数关系式:
(1)y = 3 + 0.5x; (2) y = 100-0.18x.
(3) h = 0.5n; (4) T = -2t.
一般地,形如 y = kx + b (k,b 为常数,k ≠ 0)的函数叫做一次函数.
当 b = 0 时,一次函数 y = kx + b 就成为 y = kx (k为常数,k ≠ 0),因此这样的函数叫做正比例函数.
一次函数:
大家讨论一下,这几个函数关系式有什么关系
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4;
(2)y=5x2-6;
(3)y=2πx;
(6)y=8x2+x(1-8x)
练一练
(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例1 已知 y 关于 x 的函数 y=(m-5)xm -24+m+1.
(1)若它是一次函数,求 m 的值;
(2)若它是正比例函数,求 m 的值.
解: 因为 y=(m-5)xm -24+m+1是一次函数,
所以 m2-24=1且m-5 ≠ 0.
所以 m=±5且 m ≠ 5.
所以 m=-5.
所以,当 m=-5 时,函数 y=(m-5)xm -24+m+1 是一次函数.
(2)若它是正比例函数,求 m 的值.
解:因为 y=(m-5)xm -24+m+1 是正比例函数,
所以 m2-24=1且 m-5 ≠ 0 且 m+1=0.
所以 m=±5且 m ≠ 5 且 m=-1.
则这样的 m 不存在,
所以函数 y=(m-5)xm -24+m+1 不可能为
正比例函数.
【方法总结】函数是一次函数,则 k ≠ 0,且自变量的次数为 1.当 b=0 时,一次函数为正比例函数.
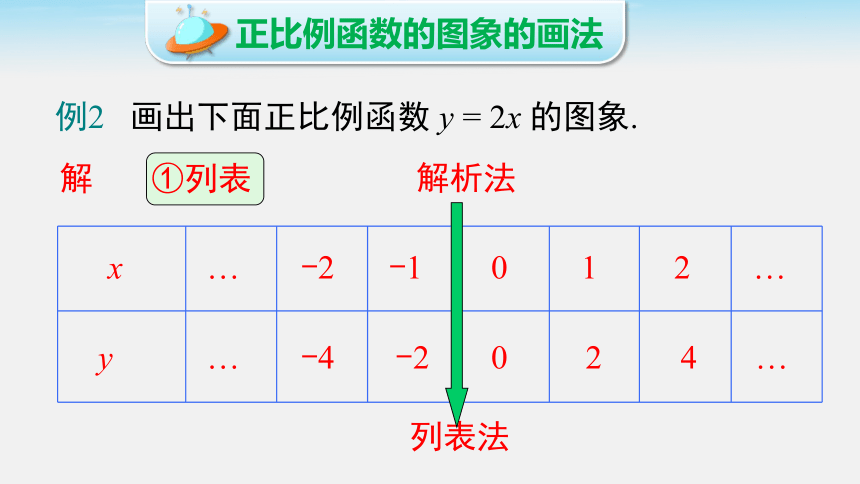
例2 画出下面正比例函数 y = 2x 的图象.
解
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解析法
列表法
①列表
正比例函数的图象的画法
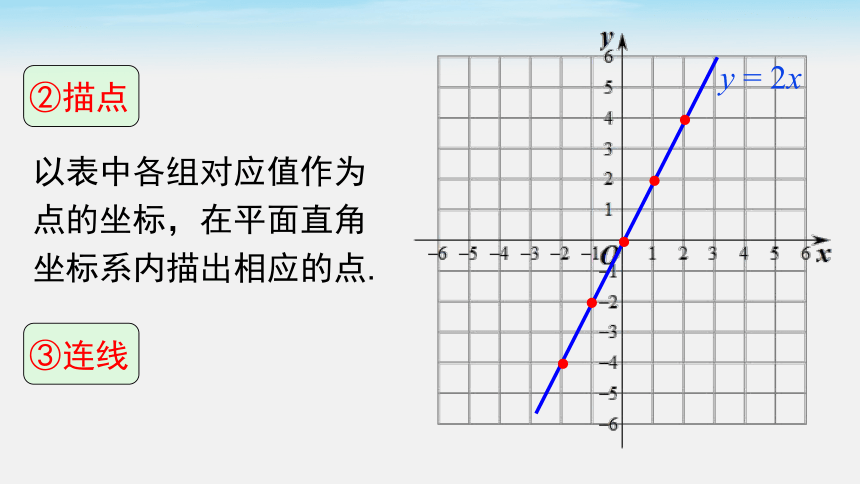
y = 2x
②描点
以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点.
③连线
画函数图象的一般步骤:
①列表
②描点
③连线
根据这个步骤画出函数 y = -3x 的图象
要点归纳
y = 2x
y = -3x
这两个函数图象有什么共同特征?
归纳总结
y = kx (k 是常数,k ≠ 0) 的图象是一条经过原点的直线 y = kx (k ≠ 0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
怎样画正比例函数的图象最简单?为什么?
由于两点确定一条直线,画正比例函数图象时我们只需描点 (0,0) 和点 (1,k),连线即可.
两点
作图法
例3 在同一直角坐标系中,画出下列函数的图象:
(1) ;(2) y = x ; (3)y = 3x.
x 0 1
y = x 1
y = 3x 0
0
3
0
y = 3x
y = x
例4 已知正比例函数 y = (m + 1)xm2 ,它的图象经过第几象限?
解:因为该函数是正比例函数
m2 = 1
所以{
m + 1 ≠ 0
所以根据正比例函数图象的特点,由 k>0 可得该图象经过一、三象限.
解得 m =1,所以 m + 1 = 2>0.
(1)若函数图象经过第一、三象限,则 k 的取值
范围是________.
变式1: 已知正比例函数 y = (k + 1)x.
k>-1
(2)若函数图象经过点(2,4),则 k_____.
解析:因为函数图象经过第一、三象限,所以
k + 1>0,解得 k>-1.
解析:将坐标(2,4)带入函数表达式中,得
4 = (k + 1)·2,解得 k = 1.
= 1
变式2:当 x>0 时,y 与 x 的函数解析式为 y = 2x ,
当 x≤0 时,y 与 x 的函数解析为 y = -2x ,则在同一直角坐标系中的图象大致为 ( )
C
x
y
O
O
O
O
x
x
y
y
y
A
B
C
D
这四个函数中,随着 x 的增大,y的值分别如何变化?
画一画:在同一直角坐标系内画出正比例函数 y = x,y = 3x,y = - x 和 y = -4x 的图象.
正比例函数图象的性质
x 增大,y 的值也增大;
x 增大,y 的值反而减小.
y 随 x 的增大而增大
y 随 x 的增大而减小
想一想:下列函数中,随着 x 的增大,y 的值分别如何变化?
当 k>0时,
当 k<0时,
x
y
O
y = 2x
1
2
2
4
2
4
y = x
3
2
-3
-6
x
y
O
在正比例函数 y = kx (k 为常数,k ≠ 0)中,
当 k>0 时,y 的值随着 x 值的增大而增大
(图象是自左向右上升的);
当 k<0时,y 的值随着 x 值的增大而减小
(图象是自左向右下降的).
总结归纳
(1)正比例函数 y = x 和 y = 3x 中,随着 x 值的增大 y 的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数 y = - x 和 y = -4x 中,随着 x 值的增大 y 的值都减小了,其中哪一个减小得更快?你是如何判断的?
| k |越大,直线越陡,直线越靠近 y 轴.
议一议
练一练
1.已知正比例函数 y = kx (k>0) 的图象上有两点(x1,y1),
(x2,y2),若 x1<x2,则 y1 y2.
<
2. 正比例函数 y = k1x 和 y = k2x 的图
象如图,则 k1和 k2 的大小关系是( )
A. k1>k2 B. k1 = k2
C. k1<k2 D. 不能确定
y = k1x
y = k2x
x
y
O
A
例5 已知正比例函数 y = mx 的图象经过点(m,4),且 y 的值随着 x 值的增大而减小,求 m 的值.
解:因为正比例函数 y = mx 的图象经过点(m,4),
所以 4 = m·m,解得 m =±2.
又 y 的值随着 x 值的增大而减小,
所以 m<0,故 m =-2.
1.下列图象哪个可能是函数 y = -x 的图象( )
B
2.对于正比例函数 y = (k - 2)x,当 x 增大时,y 随 x 的增大而增大,则 k 的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
C
3.函数 y = -7x 的图象经过第_________象限,经过点
_______与点 ,y 随 x 的增大而_______.
二、四
(0,0)
(1,-7)
减小
4.已知正比例函数 y = (2m + 4)x.
(1)当 m ,函数图象经过第一、三象限;
(2)当 m ,y 随 x 的增大而减小;
(3)当 m ,函数图象经过点(2,10).
>-2
<-2
= 0.5
5. 如图分别是函数 y = k1 x,y = k2 x,y = k3 x,y = k4 x 的图象.
(1)k1 k2,k3 k4
(填“>”或“<”或“=”);
(2)用不等号将 k1, k2,
k3, k4 及 0 依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y = k4 x
-4
-2
2
y = k3 x
y = k2 x
y = k1 x
<
6. 已知函数 y = (m - 1)x + 1 - m2
(2)当 m 为何值时,这个函数是正比例函数
(1)当 m 为何值时,这个函数是一次函数
解:(1)由题意可得
m - 1 ≠ 0,解得 m ≠ 1.
(2)由题意可得
m - 1 ≠ 0,1 - m2 = 0,解得 m = -1.
即 m ≠ 1 时,这个函数是一次函数.
即 m = -1 时,这个函数是正比例函数.
7. 已知某种小汽车的耗油量是每 100 km 耗油 15 L.所使用的汽油为 5 元/ L .
(1)写出汽车行驶途中所耗油费 y(元)与行程
x(km)之间的函数关系式.
(2)在平面直角坐标系内描出大致的函数图象.
(3)计算该汽车行驶 220 km 所需油费是多少.
y/元
x/km
1 2 3 4 5 6 7
6
5
4
3
2
1
O
(1)y = 5×15 x ÷100,
即 (x≥0).
(2)
x 0 4
y 0 3
列表
(3)当 x = 220时,
答:该汽车行驶 220 km 所需油费是 165 元.
描点
连线
(元).
解:
正比例函数的图象和性质
正比例函数: y = kx ( k ≠ 0 )
图象:经过原点的直线.
一次函数:y = kx + b
( k、b 为常数,且 k ≠ 0 )
当 k>0 时,y 的值随着 x 值的增大而增大;
当 k<0 时,y 的值随着 x 值的增大而减小.
第1课时 正比例函数的图象和性质
第12章 一次函数
12.2 一次函数
1.函数有哪些表示方法?
图象法、列表法、解析法
三种方法可以相互转化
它们之间有什么关系?
2.你能将解析法转化成图象法吗?
什么是函数的图象?
在现实生活当中有许多问题都可以归结为函数问题,大家能不能举一些例子
一次函数与正比例函数
情景一:某弹簧的自然长度为 3 cm,在弹性限度内,所挂物体的质量 x 每增加 1 kg,弹簧长度 y 增加 0.5 cm.你能写出 y 与 x 之间的关系吗?
y = 3 + 0.5x
情景二:某辆汽车油箱中原有油 100 L,汽车每行驶 50 km 耗油 9 L.设汽车行使路程 x (km),油箱剩余油量 y (L),你能写出 y 与 x 的关系吗?
y =100-0.18x
情景三:每个练习本的厚度为 0.5 cm,一些练习本摞
在一起的总厚度 h(单位:cm)随练习本的本数 n 的
变化而变化.写出函数解析式.
情景四:冷冻一个 0 ℃ 的物体,使它每分钟下降 2 ℃,
物体问题 T(单位:℃)随冷冻时间 t(单位:min)
的变化而变化.写出函数解析式.
h = 0.5n
T = -2t
上面的四个函数关系式:
(1)y = 3 + 0.5x; (2) y = 100-0.18x.
(3) h = 0.5n; (4) T = -2t.
一般地,形如 y = kx + b (k,b 为常数,k ≠ 0)的函数叫做一次函数.
当 b = 0 时,一次函数 y = kx + b 就成为 y = kx (k为常数,k ≠ 0),因此这样的函数叫做正比例函数.
一次函数:
大家讨论一下,这几个函数关系式有什么关系
下列关系式中,哪些是一次函数,哪些是正比例函数?
(1)y=-x-4;
(2)y=5x2-6;
(3)y=2πx;
(6)y=8x2+x(1-8x)
练一练
(1)是一次函数,不是正比例函数;
(2)不是一次函数,也不是正比例函数;
(3)是一次函数,也是正比例函数;
(4)是一次函数,也是正比例函数;
(5)不是一次函数,也不是正比例函数;
(6)是一次函数,也是正比例函数.
方法总结
1.判断一个函数是一次函数的条件:
自变量是一次整式,一次项系数不为零;
2.判断一个函数是正比例函数的条件:
自变量是一次整式,一次项系数不为零,常数项为零.
例1 已知 y 关于 x 的函数 y=(m-5)xm -24+m+1.
(1)若它是一次函数,求 m 的值;
(2)若它是正比例函数,求 m 的值.
解: 因为 y=(m-5)xm -24+m+1是一次函数,
所以 m2-24=1且m-5 ≠ 0.
所以 m=±5且 m ≠ 5.
所以 m=-5.
所以,当 m=-5 时,函数 y=(m-5)xm -24+m+1 是一次函数.
(2)若它是正比例函数,求 m 的值.
解:因为 y=(m-5)xm -24+m+1 是正比例函数,
所以 m2-24=1且 m-5 ≠ 0 且 m+1=0.
所以 m=±5且 m ≠ 5 且 m=-1.
则这样的 m 不存在,
所以函数 y=(m-5)xm -24+m+1 不可能为
正比例函数.
【方法总结】函数是一次函数,则 k ≠ 0,且自变量的次数为 1.当 b=0 时,一次函数为正比例函数.
例2 画出下面正比例函数 y = 2x 的图象.
解
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解析法
列表法
①列表
正比例函数的图象的画法
y = 2x
②描点
以表中各组对应值作为点的坐标,在平面直角坐标系内描出相应的点.
③连线
画函数图象的一般步骤:
①列表
②描点
③连线
根据这个步骤画出函数 y = -3x 的图象
要点归纳
y = 2x
y = -3x
这两个函数图象有什么共同特征?
归纳总结
y = kx (k 是常数,k ≠ 0) 的图象是一条经过原点的直线 y = kx (k ≠ 0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
怎样画正比例函数的图象最简单?为什么?
由于两点确定一条直线,画正比例函数图象时我们只需描点 (0,0) 和点 (1,k),连线即可.
两点
作图法
例3 在同一直角坐标系中,画出下列函数的图象:
(1) ;(2) y = x ; (3)y = 3x.
x 0 1
y = x 1
y = 3x 0
0
3
0
y = 3x
y = x
例4 已知正比例函数 y = (m + 1)xm2 ,它的图象经过第几象限?
解:因为该函数是正比例函数
m2 = 1
所以{
m + 1 ≠ 0
所以根据正比例函数图象的特点,由 k>0 可得该图象经过一、三象限.
解得 m =1,所以 m + 1 = 2>0.
(1)若函数图象经过第一、三象限,则 k 的取值
范围是________.
变式1: 已知正比例函数 y = (k + 1)x.
k>-1
(2)若函数图象经过点(2,4),则 k_____.
解析:因为函数图象经过第一、三象限,所以
k + 1>0,解得 k>-1.
解析:将坐标(2,4)带入函数表达式中,得
4 = (k + 1)·2,解得 k = 1.
= 1
变式2:当 x>0 时,y 与 x 的函数解析式为 y = 2x ,
当 x≤0 时,y 与 x 的函数解析为 y = -2x ,则在同一直角坐标系中的图象大致为 ( )
C
x
y
O
O
O
O
x
x
y
y
y
A
B
C
D
这四个函数中,随着 x 的增大,y的值分别如何变化?
画一画:在同一直角坐标系内画出正比例函数 y = x,y = 3x,y = - x 和 y = -4x 的图象.
正比例函数图象的性质
x 增大,y 的值也增大;
x 增大,y 的值反而减小.
y 随 x 的增大而增大
y 随 x 的增大而减小
想一想:下列函数中,随着 x 的增大,y 的值分别如何变化?
当 k>0时,
当 k<0时,
x
y
O
y = 2x
1
2
2
4
2
4
y = x
3
2
-3
-6
x
y
O
在正比例函数 y = kx (k 为常数,k ≠ 0)中,
当 k>0 时,y 的值随着 x 值的增大而增大
(图象是自左向右上升的);
当 k<0时,y 的值随着 x 值的增大而减小
(图象是自左向右下降的).
总结归纳
(1)正比例函数 y = x 和 y = 3x 中,随着 x 值的增大 y 的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数 y = - x 和 y = -4x 中,随着 x 值的增大 y 的值都减小了,其中哪一个减小得更快?你是如何判断的?
| k |越大,直线越陡,直线越靠近 y 轴.
议一议
练一练
1.已知正比例函数 y = kx (k>0) 的图象上有两点(x1,y1),
(x2,y2),若 x1<x2,则 y1 y2.
<
2. 正比例函数 y = k1x 和 y = k2x 的图
象如图,则 k1和 k2 的大小关系是( )
A. k1>k2 B. k1 = k2
C. k1<k2 D. 不能确定
y = k1x
y = k2x
x
y
O
A
例5 已知正比例函数 y = mx 的图象经过点(m,4),且 y 的值随着 x 值的增大而减小,求 m 的值.
解:因为正比例函数 y = mx 的图象经过点(m,4),
所以 4 = m·m,解得 m =±2.
又 y 的值随着 x 值的增大而减小,
所以 m<0,故 m =-2.
1.下列图象哪个可能是函数 y = -x 的图象( )
B
2.对于正比例函数 y = (k - 2)x,当 x 增大时,y 随 x 的增大而增大,则 k 的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
C
3.函数 y = -7x 的图象经过第_________象限,经过点
_______与点 ,y 随 x 的增大而_______.
二、四
(0,0)
(1,-7)
减小
4.已知正比例函数 y = (2m + 4)x.
(1)当 m ,函数图象经过第一、三象限;
(2)当 m ,y 随 x 的增大而减小;
(3)当 m ,函数图象经过点(2,10).
>-2
<-2
= 0.5
5. 如图分别是函数 y = k1 x,y = k2 x,y = k3 x,y = k4 x 的图象.
(1)k1 k2,k3 k4
(填“>”或“<”或“=”);
(2)用不等号将 k1, k2,
k3, k4 及 0 依次连接起来.
<
解: k1<k2 <0<k3 <k4
4
2
-2
-4
4
x
y
O
y = k4 x
-4
-2
2
y = k3 x
y = k2 x
y = k1 x
<
6. 已知函数 y = (m - 1)x + 1 - m2
(2)当 m 为何值时,这个函数是正比例函数
(1)当 m 为何值时,这个函数是一次函数
解:(1)由题意可得
m - 1 ≠ 0,解得 m ≠ 1.
(2)由题意可得
m - 1 ≠ 0,1 - m2 = 0,解得 m = -1.
即 m ≠ 1 时,这个函数是一次函数.
即 m = -1 时,这个函数是正比例函数.
7. 已知某种小汽车的耗油量是每 100 km 耗油 15 L.所使用的汽油为 5 元/ L .
(1)写出汽车行驶途中所耗油费 y(元)与行程
x(km)之间的函数关系式.
(2)在平面直角坐标系内描出大致的函数图象.
(3)计算该汽车行驶 220 km 所需油费是多少.
y/元
x/km
1 2 3 4 5 6 7
6
5
4
3
2
1
O
(1)y = 5×15 x ÷100,
即 (x≥0).
(2)
x 0 4
y 0 3
列表
(3)当 x = 220时,
答:该汽车行驶 220 km 所需油费是 165 元.
描点
连线
(元).
解:
正比例函数的图象和性质
正比例函数: y = kx ( k ≠ 0 )
图象:经过原点的直线.
一次函数:y = kx + b
( k、b 为常数,且 k ≠ 0 )
当 k>0 时,y 的值随着 x 值的增大而增大;
当 k<0 时,y 的值随着 x 值的增大而减小.
